基于Copula函数的比特币与黄金价格相关性研究

Research on Correlation between Bitcoin and Gold Price Based on Copula Function

摘要: 目的：研究比特币与黄金价格的相关性。方法：运用Eviews8.0获得样本一些描述性统计特征，分布特性，确定两变量边缘分布模型，应用多元Copula函数估计线性相关参数，通过欧氏距离最小原则确定最佳模型。结果：在三种阿基米德Copula函数中，Gubel Copula函数的欧氏距离最小，选择Gubel Copula对两者相关性分析较为合适。结论：比特币与黄金价格具有正相关关系，但是并不显著，长时间趋势内认为两者保持协同运动。不排除短期突发情况影响。

Abstract: Purpose: To study the correlation between Bitcoin and gold prices. Method: Use Eviews8.0 to obtain some descriptive statistical characteristics and distribution characteristics of the sample, determine the two-variable marginal distribution model, apply the multivariate Copula function to estimate the linear correlation parameters, and determine the best model through the minimum Euclidean distance principle. Results: Among the three Archimedes Copula functions, the Euclidean distance of the Gumbel Copula function is the smallest. It is more appropriate to analyze the correlation between Bitcoin and gold prices. Conclusion: Bitcoin and gold prices have a positive correlation, but it is not significant. In the long-term trend, it is believed that the two will maintain a coordinated movement, and the impact of short-term emergencies cannot be ruled out.

1. 引言

自2008年日本学者中本聪挖掘出第一枚比特币后至今已过去十多年的时间，但是国际上目前对于以比特币为代表的加密数字货币的属性仍未有统一的标准。截止 2020 年 12 月 31 日 ，加密数字货币市场统计网站coinmarketcap.com上，加密数字货币种类达4037种，其中有市场价值的2319种，随着新型加密数字货币数量的不断上升，加密数字货币市场的不断扩展，受众群和交易频率，种类等方面巨大增涨的情况下，这一情况是不容忽视的。以比特币为代表的加密数字货币自2009年发行以来其价格变动，涨跌幅度过度大，行情犹如过山车，比特币的日收盘价可以在两个月时间上涨10倍，也能在仅仅一周之内下滑80%，这对于短期投资者是具有很大的风险， 2015 年 1 月 22 日 比特币价格172.7美元至 2020 年 12 月 31 日 价格为28,841.57美元，两者相差167倍，直观的对比比特币价格，可知比特币价格波动明显。加密数字货币市场的混乱现象给普通投资者、经济学家、企业家及政府多方面均带来了新的挑战与机遇。这也表示对于以比特币资产定价模型的研究是十分有意义的。

随着比特币市场的发展壮大，对以比特币为代表的加密数字货币的相关研究关注度越来越多，由于本文主要研究比特币与黄金价格变动之间的关系，于是本文主要介绍有关研究比特币和黄金相关性的文献。Al-Khazali [1] 等研究了宏观经济新闻对比特币和黄金的回报率和波动性的影响。Henriques和Sadorsky [2] 则应用GARCH模型研究在投资组合中比特币是否可以对替代黄金，证明具有替代性，甚至可能获得更高的风险调整回。Sahin Telli，Hongzhuan Chen [3] 应用MFDFA模型研究比特币和黄金的收益率和波动率系列的性质，及其决定因素。发现比特币收益率与黄金收益率相比具有明显不同的多重份特性。Sang Hoon Kang [4] 利用GARCH模型的动态条件相关(DCC)和小波相关方法，建立模型检测黄金期货和比特币收益率之间的潜在因果关系。发现了比特币和黄金期货价格之间的波动持续性，因果关系和相位差的证据。Dyhrberg [5] 发现相对于黄金和货币市场，比特币市场行为的对冲特性，认为比特币性质介于黄金和美元之间。同年Dyhrberg [6] 在前面论文的基础上用非对称GARCH模型，研究了比特币与股票市场的对冲特性。Francisco Jareno [7] 采用2010~2018年比特币和黄金收益率，发现在极端市场条件下，比特币收益率更加敏感。比特币和黄金收益率存在正向相关性，统计上十分显著。

本文应用Copula模型进行相关性分析，Copula模型开始于国外学者的研究先应用于国外金融市场之间金融变量的相关性方面研究。Patton [8] 建立二元Copula模型分析美元，日元的收益率之间的相关性，并于传统的格兰杰因果模型结果作对比，发现Copula模型更贴合实际现象。Rockinger和Jondeau [9] 建立了Copula-GARCH模型，研究金融变量之间的动态相关关系并计算风险价值，通过度量发现t-Copula比传统的模型更好的刻画相关性。Melike [10] 研究石油和股票日收益率序列，使用GARCH，Copula两模型结合方法，研究两者的动态关系。结果说明石油价格的波动性、股票收益率和投资者预期之间存在显著的，非线性尾部相关关系。当然随着模型的发展，国内学者对Coupla也开始了研究，张尧庭 [11] 首次将Copula函数应用于中国市场。先介绍了Copula函数在金融市场，特别是股票市场中的应用。罗俊鹏 [12] 对英镑和欧元的组合相关性使用Copula-GARCH-GPD模型进行了研究，认为Copula-GARCH-GPD模型可以很好的描述变量的边缘分布及相关关系。鲁万波 [13] 用Copula理论建立不等间隔日期内的投资组合波动率模型，并捕获在横截面上的资产组合中各资产的相关关系，并应用蒙特卡洛模拟计算出其在险价值。

从上述文献可以看出目前国内对于比特币和黄金之间关系的研究较少。传统的线性模型和Granger因果关系，在捕获金融市场变量之间的相关关系时存在限制性，有可能导致结论的错误，线性模型应用的前提：变量之间是线性关系，且有方差有限存在的，但目前金融市场的情况是：许多金融变量序列的方差是：不存在的，非线性的，多呈尖峰，厚尾等特征；Garnger因果关系的前提是研究变量属于小样本数据，并且只可以给出定性的分析，不可以得到定量的结论。由于目前的市场大背景状况，文章在获取比特币和黄金价格之间的相关关系时，采用Copula函数进行一系列的相关性分析，这也是自2015以后国内外在研究变量之间相关性关系应用较多的方法，较传统的方法，理论模型，相关结构更可靠，更具有优势。

2. Copula函数

2.1. Copula函数简介

Sklar最早提出Copula函数，1959年他给出了Copula理论：可以将具有k个随机变量的联合分布分解为它的一个连接函数和k个边缘分布，这个函数就是Copula函数(又叫连接函数)，它可以捕捉变量之间的相关关系 [14]。1999年Nelsen对Copula函数的定义，性质和有关理论进行了全面总结，并提出了阿基米德Copula函数，使Copula函数更加完整。

定理1：令 $F\left(x_1,x_2,\cdots ,x_n\right)$ 是联合分布函数， $F_1\left(x_1\right),F_2\left(x_2\right),\cdots ,F_N\left(x_N\right)$ 分别是它的N个边缘分布函数，那么存在一个Copula函数 $C\left(u_1,u_2,\cdots ,u_N\right)$ 定义域内任意 $\left(u_1,u_2,\cdots ,u_N\right)$ 有：

$C\left(u_1,u_2,\cdots ,u_N\right)=F\left(F_1^{\left(-1\right)}\left(u_1\right),F_2^{\left(-1\right)}\left(u_2\right),\cdots ,F_N^{\left(-1\right)}\left(u_N\right)\right)$ (1)

2.2. 常用的Copula函数

本节介绍几种比较常用的Copula函数，如二元正态Copula函数和几种重要的二元阿基米德(Archimedean) Copula函数。

2.2.1. 二元正态Copula函数

二元正态Copula函数的分布函数 [15] 为：

$C\left(u,v,\rho \right)={\displaystyle {\int }_{-\infty }^{{\varphi }^{-1}\left(u\right)}{\displaystyle {\int }_{-\infty }^{{\varphi }^{-1}\left(v\right)}\frac{1}{2\pi \sqrt{1-{\rho }^2}}\exp \left(\frac{-\left(r^2+s^2-2\rho rs\right)}{2\left(1-{\rho }^2\right)}\right)\text{d}r\text{d}s}}$ (2)

二元正态Copula函数的密度函数为：

$c\left(u,v,\rho \right)=\frac{1}{\sqrt{1-{\rho }^2}}\exp \left(-\frac{{\varphi }^{-1}\left(u^2\right)+{\varphi }^{-1}\left(v^2\right)-2\rho {\varphi }^{-1}{\left(u\right)}^2{\varphi }^{-1}{\left(v\right)}^2}{2\left(1-{\rho }^2\right)}\right)\exp \left(-\frac{{\varphi }^{-1}{\left(u\right)}^2{\varphi }^{-1}{\left(v\right)}^2}{2}\right)$ (3)

二元正态Copula函数在描述相关性较为普遍应用，由于它对样本数据有很好的拟合效果，然而遗憾的是，由于二元正态Copula函数具有对称性，只能描述变量间的对称相关关系，对金融市场变量间非对称的相关关系的描述无能为力。

2.2.2. 阿基米德函数

阿基米德Copula函数是由Genest和Mackay在1986年提出的，具体表达式 [15] 为：

$C\left(u_1,u_2,\cdots ,u_n\right)={\phi }^{-1}\left(\phi \left(u_1\right)+\phi \left(u_2\right)+\cdots +\phi \left(u_n\right)\right)$ (4)

其中 $\phi$ 为阿基米德Copula函数的母函数，需要满足下面的三个条件：

1) ${\displaystyle \underset{n=1}{\overset{N}{\sum }}\phi \left(u_n\right)}\le \phi \left(0\right)$ 且 $\phi \left(1\right)=0$

2) $\forall t\in \left[0,1\right]$ 有 ${\phi }^{\prime }\left(t\right)<0$， ${\phi }^{″}>0$，即母函数是一个凸的减函数

3) ${\phi }^{-1}\left(t\right)$ 是 $\phi \left(t\right)$ 的逆函数，在 $\left[0,\infty \right)$ 区间内完全单调

凡是满足上式的Copula函数均称为阿基米德Copula函数。从上式可以看出，母函数是确定阿基米德Copula函数的唯一元素。阿基米德函数是一个函数族，基于本文的应用，下面只列举比较常用的三种二元阿基米德Copula函数：Gumbel Copula函数，Clyton Copula函数，Frank Copula函数。

Gumbel Copula函数的分布函数为：

$C_G\left(u,v,\alpha \right)=\exp \left(-{\left[{\left(-\ln u\right)}^{\frac{1}{\alpha }}+{\left(-\ln v\right)}^{\frac{1}{\alpha }}\right]}^{\alpha }\right)$ (5)

Gumbel Copula函数的密度函数为：

$c_G=\frac{C_G\left(u,v,\alpha \right){\left(\ln u\cdot \ln v\right)}^{\frac{1}{\alpha }-1}}{uv{\left[{\left(-\ln u\right)}^{\frac{1}{\alpha }}+{\left(-\ln v\right)}^{\frac{1}{\alpha }}\right]}^{2-\alpha }}\left\{\left[{\left(-\ln u\right)}^{\frac{1}{\alpha }}+{\left(-\ln v\right)}^{\frac{1}{\alpha }}\right]+\frac{1}{\alpha }-1\right\}$ (6)

Gumbel Copula函数的密度函数展现“J”字型，上尾高下尾低，也就是说分布的上尾会更加敏感，上尾比下尾更加强烈，可以更快速的反应，同时具有非对称性。

Clyton Copula函数的分布函数为：

$C_{Cl}\left(u,v,\theta \right)={\left(u^{-\theta }+v^{-\theta }-1\right)}^{-\frac{1}{\theta }}$ (7)

Clyton Copula函数的密度函数为：

$c_{Cl}\left(u,v,\theta \right)=\left(1+\theta \right){\left(uv\right)}^{-\theta -1}{\left(u^{-\theta }+v^{-\theta }-1\right)}^{-2-\frac{1}{\theta }}$ (8)

与Gumbel Copula函数相同的是，Clyton Copula函数具有非对称性，不同的是它是上尾低下尾高。也就是说它在描述变量相关性时，在分布的下尾部会更加明显和敏感，对下尾部的相关性能够给予快速的反应。由Clyton Copula函数描述变量之间的相关关系，说明这两个变量较强的相关性体现在下尾部，在上尾部几乎是不相关的。

Frank Copula函数的分布函数为：

$C_F\left(u,v,\lambda \right)=-\frac{1}{\lambda }\ln \left(1+\frac{\left({\text{e}}^{-\lambda u}-1\right)\left({\text{e}}^{-\lambda v}-1\right)}{{\text{e}}^{-\lambda }-1}\right)$ (9)

Frank Copula函数的密度函数为：

$c_F\left(u,v,\lambda \right)=\frac{-\lambda \left({\text{e}}^{-\lambda }-1\right){\text{e}}^{-\lambda \left(u+v\right)}}{\left[\left({\text{e}}^{-\lambda }-1\right)+\left({\text{e}}^{-\lambda u}-1\right)\left({\text{e}}^{-\lambda v}-1\right)\right]}$ (10)

Frank Copula函数与Gumbel Copula和Clyton Copula函数不同的是具有对称性，呈现“U”字型，只能描述随机变量之间的对称性，对于非对称的无能为力与二元正态Copula一致。

2.3. 关于Copula函数的相关性测度

本文主要介绍常用的两个相关性测度：Kendall秩，Spearman秩相关系数。这两个都是由Copula函数导出的相关性测度，都有严格单调増变换条件下不变的特点，这也是Copula函数研究相关性的一个优势。

Kendall秩相关系数 [16]

定义1：设 $\left(x_1,y_1\right)$ 和 $\left(x_2,y_2\right)$ 是独立同分布的随机变量，则

$\tau =P\left[\left(x_1-x_2\right)\left(y_1-y_2\right)>0\right]-P\left[\left(x_1-x_2\right)\left(y_1-y_2\right)<0\right]$ (11)

为Kendall秩相关系数 $\tau$。

Spearman秩相关系数 [16]

定义2：设随机变量X，Y的边缘分布分别为 $F\left(x\right),F\left(y\right)$ 相应的Copula函数 $C\left(u,v\right)$，其中 $u=F\left(x\right)$， $v=G\left(y\right)$， $u,v\in \left[0,1\right]$ 则有

$\rho =12{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{1}uv\text{d}C\left(u,v\right)}}-3=12{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{1}C\left(u,v\right)\text{d}uv}}-3$ (12)

3. 实证分析

3.1. 研究思路

首先利用基础数据也就是 2017 年 8 月 1 日 至 2020 年 3 月 22 日 的比特币日价格和黄金价格计算出对数日收益率，运用eviews8.0软件，获得样本的一些统计特性，分布特性，分析结果，确定并建立黄金和比特币价格对数日收益率的边缘分布模型，接着运用Matlab 9.2.0 软件进行Copula函数的选取，分别用二元正态Copula函数，t-Copula函数，Gumbel Copula函数，Clayton Copula函数及Frank Copula函数对模型进行估计，通过估计线性相关参数，计算相关测度等比较5个模型的建模效果，并通过欧氏距离最短原则，选择出一个最佳拟合模型。最后得出黄金价格与比特币之间的相关关系。

3.2. 数据来源与选择

本文样本选择 2017 年 8 月 1 日 至 2020 年 3 月 22 日 的比特币日价格和黄金价格为基础数据。比特币日交易价格由数字货币统计网站coinmarketcap.com提供，黄金每个交易日收盘价由国泰安数据库(CSMAR)提供。

就模型的建立与估计的方法本身而言，样本容量越大，估计结果越贴近实际。但是在较长的时间内，交易信息中可能包含的偶发事件造成的噪音影响，为了统合考虑这两个维度，使数据真实可靠，文章最终确定选取的为 2017 年 8 月 1 日 至 2020 年 3 月 22 日 这个时间段的数据。

3.3. 模型选择

利用eviews8.0软件做出比特币和黄金价格对数日收益率的单位根检验判断数据是否具有平稳性得出表1，从表1可以看出黄金和比特币收益率的t统计量比1%，5%，10%检验水平下的临界值都要小，对应的概率值也小于0.05，即两序列均无单位根的，通过平稳性检验。通过描述性统计并分析结果，由图1可以看出比特币对数收益率序列均值为0.079704，偏度为−1.029290，小于0表示序列不对称，左拖尾较长，峰度为16.24033远远超过了3，显然序列是厚尾的，存在一定的偏斜，初步判断序列均不服从正态分布。由图2黄金价格对数收益率的直方分布图及一些基本统计特征的结果可以看出，序列J-B统计量为22,702.14，P值为0.000000，则在5%的置信水平下拒绝H0：服从正态分布的原假设，确定序列不服从正态分布。

Table 1. ADF stationary test statistics

表1. ADF平稳性检验统计量

Figure 1. Descriptive statistics of Bitcoin

图1. 比特币描述性统计图

Figure 2. Descriptive statistics of Gold

图2. 黄金描述性统计图

观察比特币和黄金的QQ图(图3，图4)，可以知道序列拟合度不高，有偏离直线的情况，明显不服从正态分布，因此当总体分布不确定时需利用经验分布来近似总体分布。通过图5和图6可以看出经验分布函数和核密度估计拟合度高，正说明对确定变量分布核密度估计具有一定的高效性。

Figure 3. QQ graph of Bitcoin yield

图3. 比特币收益率QQ图

Figure 4. QQ graph of gold yield

图4. 黄金收益率QQ图

通过图7二元频率直方图，图8 (U, V)二元分布直方图可以看出，频率直方图具有非对称的尾部特征，故本文放弃利用对称尾部特征的Copula函数，选择使用具有非对称尾部特征的Copula函数来描述比特币和黄金的相关关系。并且从表2中也可以看出在三种阿基米德Copula函数中，Gumbel Copula函数的平方欧氏距离最小，值为0.0174。因此本文最终决定选则Gumbel Copula函数对比特币和黄金价格之间的相关结构进行描述。

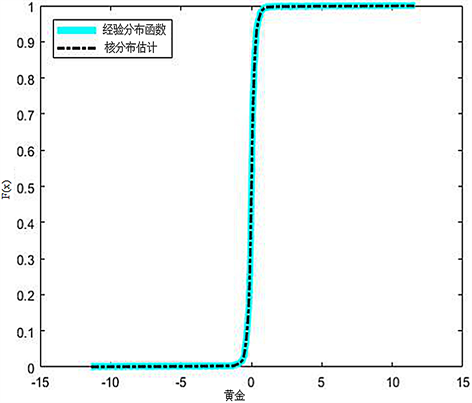
Figure 5. Bitcoin experience distribution in the nuclear distribution fitting diagram

图5. 比特币经验分布于核分布拟合图

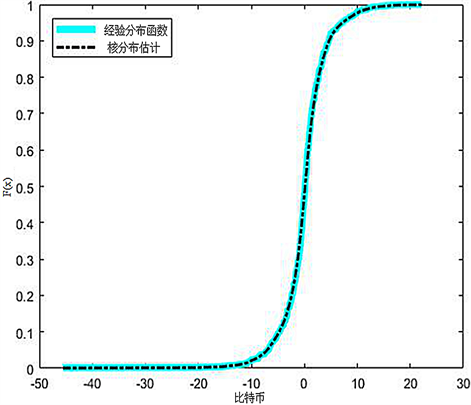
Figure 6. Fitting diagram of golden experience distribution and nuclear distribution

图6. 黄金经验分布与核分布拟合图

3.4. 模型评价

通过上文对Copula函数进行参数估计和检验，对比平方欧氏距离我们发现非对称的Copula函数Gumbel Copula函数是最佳的描述比特币和黄金价格相关关系的模型。我们可以画出Gumbel Copula函数的分布函数和密度函数，图形结果见图9，图10。

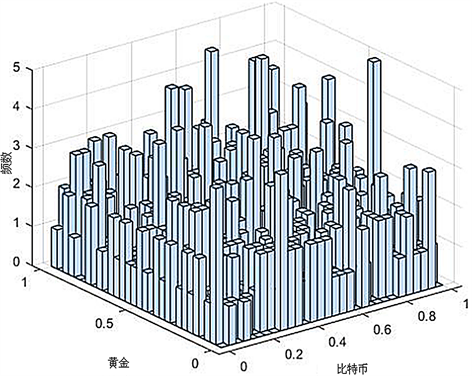
Figure 7. Binary frequency histogram of Gold and Bitcoin

图7. 黄金与比特币二元频数直方图

Figure 8. Binary distribution histogram of Bitcoin and gold edge

图8. 比特币和黄金边缘二元分布直方图

Table 2. Square Euclidean distance of three Copula functions

表2. 三种Copula函数的平方欧式距离

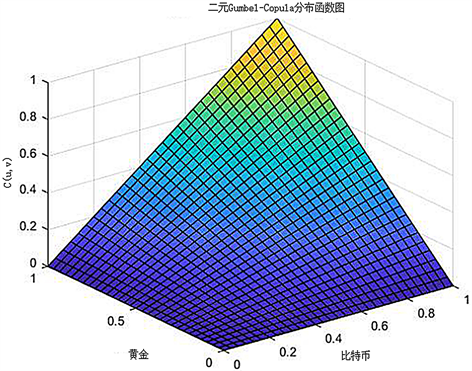
Figure 9. Bitcoin and gold distribution function graph

图9. 比特币与黄金分布函数图

Figure 10. Bitcoin and gold density function graph

图10. 比特币与黄金密度函数图

结果表明，利用Gambel Copula函数对比特币和黄金收益率序列进行相关性分析得出的Kendall秩相关系数为0.026，大于0则比特币对数日收益率同黄金的对数日收益率的变化一致的概率大于不一致概率，从长期趋势上看两者存在正相关关系，除特殊情况以外，不排除短期时间内突发状况的情况；Spearman秩为0.04为正同理可知比特币对数日收益率与黄金的变化一致的概率大于不一致概率，同时可以知道两者的边缘分布存在正相关关系。综上所述比特币与黄金对数日收益率之间存在正相关关系，意味着当比特币价格上升时会推动黄金价格上升，由于相关系数不是远远大于0，也不排除会发生当比特币价格上升时黄金价格下降的情况，不排除短时间内发生突发状况的可能性。

4. 结论

本文基于Copula函数研究比特币与黄金价格间结构的相关性，由于Copula函数在研究金融变量相关结构，关系等方面比传统的分析方法具有优势，通过测度欧氏距离最小等方面参考，最后采用Gambel Copula函数分析其相关性，得出结论比特币与黄金价格具有正相关关系，但是并不显著，长时间趋势内认为两者保持协同运动。但短时间内的不可控因素、金融危机、通货膨胀等因素的影响，两者也存在相向运动的现象。并且比特币和黄金价格的相关结构具有非对称性的尾部特征。由于短时间的突发因素影响导致比特币价格下降，当下降到一定程度之后，就会出现价格上涨的情况发生。

通过文章的分析，讨论最后得出的结论，警惕投资者在做投资时如果遇到投资项目中某一变量发生急剧变动：上涨或者下降的情况，此时就是我们应该提高警惕的时候，文章在最后也给出了具体的定量分析结果，可以说对投资者日后的投资提供了具体的量化指标。

基金项目

2017国家社会科学基金项目“新常态下基于修正的VAR商业银行市场风险测度与调控机制研究”(项目编号：17BJY235)；2017年新疆维吾尔自治区高校科研计划项目“新常态下基于修正的VaR商业银行市场风险”(项目编号：XJEDU 2017M 028)。