一种基于电成像测井图像孔隙度自动提取计算新方法

A New Method of Porosity Automatic Extraction and Calculation Based on Electrical Imaging Logging Image

摘要: 致密碳酸盐岩储层孔隙结构复杂，发育类型多，孔隙度难以精确预测。通过对电成像测井图像进行处理，采用图像处理阈值分割技术对图像采集时的偏差进行校正，并提出一种新的计算方法提取图像灰度值，并通过灰度值与常规测井电性参数的相关性来对不同算法的优度进行评估，最后根据灰度值与实测孔隙度存在的相关性建立回归模型对某区段致密碳酸盐岩孔隙度进行预测。研究结果表明，采用散点拟合法针对致密碳酸盐岩结构非均质性较强、储层类型多样等特点具有较强的适应性，对孔隙度进行提取优于其他算法。该方法不仅预测更加精确致密，也能高效的完成孔隙度解释工作，为致密碳酸盐岩储层孔隙度预测探索了一条新的途径。

Abstract: The pore structure of tight carbonate reservoir is complex and there are many types of development, so it is difficult to accurately predict the porosity. Through the processing of electrical imaging logging image, the image processing threshold segmentation technology is used to correct the deviation of image acquisition, and a new calculation method is proposed to extract the gray value of image, and the advantages of different algorithms are evaluated by the correlation between gray value and conventional logging electrical parameters. Finally, the regression model is established according to the correlation between gray value and measured porosity. The model is used to predict the porosity of tight carbonate rocks in a section. The results show that the scatter fitting method has strong adaptability to the characteristics of strong structural heterogeneity and diverse reservoir types of tight carbonate rocks, and it is superior to other algorithms in porosity extraction. This method can not only predict more accurately and compactly, but also complete porosity interpretation efficiently, which provides a new way for porosity prediction of tight carbonate reservoir.

1. 引言

孔隙度值在测井储层评价中是一个非常重要且难于准确计算的参数。对于致密碳酸盐岩储层，岩体结构中孔缝洞系统的发育程度和分布范围难以表征 [1]。目前采用常规测井参数对孔隙度进行预测的方式评价致密碳酸盐岩储层存在精度较低、测井识别难度大的问题 [2] [3]，采用神经网络等机器学习方式存在拟合程度不易控制、程序复杂 [4] [5] [6] [7] 等情况。实际应用中，在没有岩心资料的情况下很大程度上依赖于解释人员的经验，不仅对解释人员的相关业务水平要求较高，而且解释结果也参差不齐。为了最大程度地消除人为因素，提高储层评价的准确性，提取电成像测井资料特征参数对致密碳酸盐岩储层有效性进行定量评价显得尤为重要，陈义祥、李晓辉等 [8] [9] 通过电成像测井资料提取视孔隙度谱并对孔隙度进行计算。平海涛等 [10] 首次提出基于电成像孔隙度谱分析的复杂储层渗透率模型，实现了核磁共振测井与电成像测井的有机结合。本文在前人研究的基础之上，研究算法提取电成像图像数据，采用图像处理阈值分割技术 [11] 自动识别 [12] 井眼基准线，解决图像处理过程中存在的速度和精度问题 [13]，对电成像图像数据进行正弦校正，其后提取电成像图像灰度值与对应深度常规测井参数进行皮尔森、斯皮尔曼秩 [14] 相关系数检验，对灰度值提取算法进行评价。

2. 常规电成像测井孔隙度计算

2.1. 电成像测井

相比于常规测井方法，电成像测井具有独特的自身优势，可以对井周360度进行高分辨率成像。目前，微电阻率成像共有三种测井系列，它们分别是斯仑贝谢的FMI [15]、哈里伯顿的EMI、阿特拉斯的STAR-II，其测量原理相同，只是电极个数不同，对井眼的覆盖率有所差异。目前国外已经有比较成熟的软件进行人工交互式校正，目前该技术保密难以普及，大多数情况下仅提供标定后图像数据作为参考。

2.2. 孔隙度分布谱的计算

电成像的纽扣电极测量地层电导率，需要将它表示为电阻率。电成像测井电流流动方式、聚集形式及探测深度范围与常规测井中的浅侧向测井相当，可以选择浅侧向电阻率对电成像电导率进行刻度，然后再用Archie公式 [16] 对孔隙度进行标定：

$R_i=\frac{\bar{\sigma }}{{\sigma }_i}{R}_{LLS}$ (1)

式中： $R_i$ 为第i个纽扣电极刻度后的电阻率； ${\sigma }_i$ 为第i个纽扣电极预处理后的电导率； $\bar{\sigma }$ 为采样深度间隔内所有纽扣电极的电导率的均值； $R_{LLS}$ 为常规测井同一深度点浅侧向电阻率。

${\phi }^m{R}_{xo}=\frac{ab{R}_{mf}}{S_{xo}^n}$ (2)

式中：a，b为与岩性有关的系数；m为胶结指数；n为饱和度指数； $\phi$ 为孔隙度； $S_{xo}$ 为冲洗带的含水饱和度； $R_{xo}$ 为冲洗带电阻率； $R_{mf}$ 为泥浆溶液电阻率。

最后整理可得到每个纽扣电极经过标定后的孔隙度值 ${\phi }_i$

${\phi }_i=\sqrt[\begin{array}{l}m\\ \end{array}]{\frac{{\sigma }_i}{\bar{\sigma }}}\times {\phi }_0$ (3)

式中： ${\phi }_0$ 为常规浅侧向电阻率 $R_{LLS}$ 得到的孔隙度值。

通过胶结指数m，饱和度指数n，可求得到储层视孔隙度分布谱 [17]。孔隙度分布谱可以在一定程度上对地层的孔隙分布情况进行评价，其后左程吉等 [18] 利用核磁区间成像对其结果进行了进一步对比研究。

3. 电成像测井图像矫正

3.1. 电成像测井成像原理

深度及速度校正是井眼微电阻率成像资料处理的核心部分，如果仪器以一恒定的速度上提，对每一行电极进行简单的深度位移便可以校准所有的数据。事实上，电缆上提的过程中通常不可能是匀速的，由于电缆的伸、缩、晃动，仪器与井壁的碰撞，仪器会存在微量的加速度，因此各地层现象以正弦曲线的方式展现在图像上，根据这种情况，在图像上出现的不规则锯齿及倾斜，需要进行校正。

Figure 1. Schematic diagram of electrical imaging principle

图1. 电成像原理示意图

对电成像图片进行校正需对井眼基准线进行提取，并求其斜率。为提高井眼基准线的识别速度，本文用线性拟合的方法取代复杂耗时的Hough变换方法 [19]，全自动确定基准线。本文采用经典的阈值分割图像处理技术对图1右图绿色基线进行分割提取。首先通过人工交互的方式拾取原始图像含绿色基线部分并对其进行裁剪，采用MATLAB软件提取所有图像RGB三原色矩阵并将RGB值转换为HSV值，并对其结果进行直方图统计分析，最后确定其提取阈值(确定过程如下图2所示)：

Figure 2. Determination of segmentation for graphics interval

图2. 阈值分割区间确定过程

通过定量分析，确定阈值分割区间为图2右数第2图，色调(Hue)取值[0.22,0.5]，饱和度(Saturation)取值[0.5,1]，明度(Value)取值[0.5,1]。

3.2. 井眼基准线拟合

通过对分割后图像进行0~1值转换便可获取像素矩阵，以横向像素点为x轴坐标，以纵向像素点为y轴坐标，并对准线点位坐标进行提取。本文通过线性回归 [20] (regress)对该线条进行拟合并构造目标函数，确定回归方程及对应斜率k值，目标函数及拟合情况见图3：

Figure 3. Image of datum line fitting

图3. 基准线拟合示意图

3.3. 正弦矫正计算法则

对于图像的扭转可近似认定为正弦曲线，其在图像横坐标方向上为一个周期，其振幅为A，在求得井眼基准线斜率后可确定振幅A值：

$A=\alpha \times L\times \frac{{90}^{\circ }}{{360}^{\circ }}\times \tan \left({90}^{\circ }-\arctan \left(k\right)\right)$ (4)

式中： $\alpha$ 为矫正系数，取值7.1~7.5；L为图像横坐标方向像素长度；k为基准线斜率。由此可确定该周期函数的表达式(5)，由此可根据该式沿深度方向按一定长度对像素点坐标进行调整，实现对图像的矫正。

$\{\begin{array}{l}{\Delta }_y=A\times \sin \left(w\cdot x+b\right)\\ x=\frac{{180}^{\circ }}{{360}^{\circ }}\times L,{\Delta }_y=0\\ x=0,{\Delta }_y=0\end{array}$ (5)

式中： ${\Delta }_y$ 为图像纵坐标方向矫正量；x为图像横坐标方向像素坐标。

3.4. 应用效果

本文章根据上述算法结合MATLAB语言编程全自动批量处理实现了沿深度方向的灰度值精细矫正。选取某地区某井灯影组(5425~5464) m深度段进行验证，暂取横向灰度数据的算术平均值作为横坐标，如图4所示。从图4可以看出：① 电成像上反映孔隙结构的实际情况(左数2小图)与提取的灰度值(右数1小图)理论模型吻合很好，完全满足孔隙度值评价的要求；② 矫正前后同一深度对应灰度值最大偏差为27.6801，最小偏差为0.0272，在精度上奠定了后续孔隙度值解释的基础，并还原了地层界面孔隙结构的真实情况。

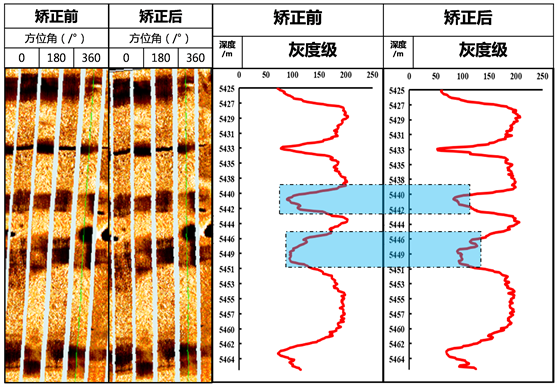
Figure 4. Comparison of electrical imaging data before and after sine correction in a logging

图4. 某井电成像图像资料正弦校正前后对比图

4. 电成像测井图像孔隙度提取算法及评价方法

4.1. 电成像测井图像数据标准化

由于各井电成像图像来源不同，以点概面难以做到严谨的科学解释，可通过将图像原始参数RGB矩阵转换为灰度值矩阵，并对各井灰度值进行直方图法分析并确定其主峰值，并根据主峰值对各井灰度值进行标准化，将各井灰度值转换到一个标准上，见图5。

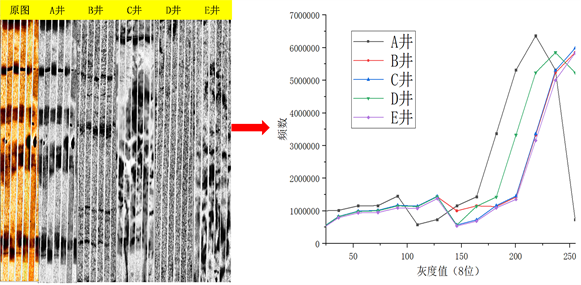
Figure 5. Gray value frequency distribution curve of each logging

图5. 各井灰度值频率分布曲线形态示意图

4.2. 实验环境

实验中使用的硬件配置如下：操作系统为Windows 10，开发语言为MATLAB 2018a，处理器型号为Intel Core i7-8570H @ 2.20 GHz四核，内存为20 GB，GPU型号为Nvidia GeForceGTX 1060 with Max-Q 6 GB。在实际操作过程中，由于电成像测井图像通常一口井分为数段，故在编写算法的时候将两张图片的原始灰度值矩阵进行拼接操作，并在深度重叠的部分采用算术平均值法进行矫正，最后得到完整的单井灰度值矩阵。

4.3. 灰度值提取算法

1) 算术平均法

算术平均法是指依次对沿深度范围一定距离间隔内灰度值进行求和，然后由得到的和除以总数得到其算术平均值为

$\bar{x}=\frac{1}{z}{\displaystyle \underset{i=1}{\overset{z_1}{\sum }}{\displaystyle \underset{j=1}{\overset{z_2}{\sum }}{x}_{ij}}}$ (6)

式中：z为距离间隔内灰度值像素点总数； $z_1$ 为沿图像横坐标方向像素点个数； $z_2$ 为沿图像纵坐标方向像素点个数。

2) 加权平均法

在计算平均值时，对每个变量设置适当的权重，然后计算其加权平均值，可以有效抑制裁剪线周边像素点的干扰，保留核心区域数据的真实度，即加权平均法。加权平均法的计算式为

$\bar{x}={\displaystyle \underset{i=1}{\overset{z_2}{\sum }}{\displaystyle \underset{j=1}{\overset{z_1}{\sum }}{\omega }_{ij}\cdot x_{ij}}}$ (7)

式中： $w_{ij}$ 为第j行i列像素点位置处对应的归一化加权值，且有 ${\displaystyle \underset{j=1}{\overset{z_1}{\sum }}{\omega }_{ij}}=1$。

3) 标准差法

对灰度值矩阵进行方差分析，求得其标准差为

$\sigma =\sqrt{\frac{1}{Z}{\displaystyle \underset{i=1}{\overset{Z}{\sum }}{\left(x_i-\mu \right)}^2}}$ (8)

式中： $\mu$ 为该像素范围内灰度值之和的算术平均值。

4) 散点拟合法

首先将距离间隔区域内的像素矩阵进行平滑滤波和降噪处理，组成一个新的平面点集，沿距离间隔区域内像素点横坐标x方向依次进行曲线拟合操作获得一条拟合曲线。如果采用最小二乘法进行曲线拟合，即令拟合误差M为

$M={\displaystyle \underset{k=1}{\overset{m}{\sum }}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left[{\left(z_i-z_{ik}\right)}^2+{\left(y_i-y_{ik}\right)}^2\right]}}$ (9)

可认为在偏导数均为零时，M可达到最小值，即

$\{\begin{array}{l}\frac{\partial M}{\partial z_i}=2{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left(z_i-z_{ik}\right)=0}\\ \frac{\partial M}{\partial y_i}=2{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left(y_i-y_{ik}\right)=0}\end{array}$ (10)

整理可得

$\{\begin{array}{l}{z}_i=\frac{1}{m}{\displaystyle \underset{k=1}{\overset{m}{\sum }}{z}_{ik}}\\ y_i=\frac{1}{m}{\displaystyle \underset{k=1}{\overset{m}{\sum }}{y}_{ik}}\end{array}$ (11)

易得

$\bar{z}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{z}_i}$ (12)

式中：n为沿距离间隔区域纵向像素点个数，m为沿距离间隔区域横向像素点个数，y为沿图像纵向像素点坐标， $z_{ik}$ 为该像素坐标处灰度值， $\bar{z}$ 为最终该间隔区域灰度提取值。

4.4. 计算方法评价

4.4.1. 皮尔森相关系数

皮尔森相关系数 $P_{XY}$ 用于衡量两个变量间线性相关性的强弱程度，用两个变量X和Y的协方差与标准差积的商来表示，如下

$P_{XY}=\frac{\mathrm{cov}\left(X,Y\right)}{{\sigma }_X{\sigma }_Y}=\frac{E\left(X-{\mu }_X\right)\left(Y-{\mu }_Y\right)}{{\sigma }_X{\sigma }_Y}$ (13)

式中： ${\mu }_X$ 、 ${\mu }_Y$ 和 ${\sigma }_X$ 、 ${\sigma }_Y$ 分别为变量X和Y的均值和标准差，且满足条件 $\left|P_{XY}\right|\le 1$， $\left|P_{XY}\right|$ 越大，表明

灰度值与常规测井电性参数的相关程度越强。

4.4.2. 斯皮尔曼秩相关系数

斯皮尔曼秩相关系数 $S_{XY}$ 用于衡量两个变量之间线性相关性的强弱程度，一般用于评价变量间的非线性相似关系，也可认为是变量通过重新排列后的Pearson线性相关系数。其计算方法是将长度均为N的两个变量X和Y按从小到大排序，分别用 $p_i$ 、 $q_i$ 表示 $x_i$ 、 $y_i$ 在排序后列表中的位置，称 $p_i$ 、 $q_i$ 为 $x_i$ 、 $y_i$ 的秩次，将各秩次代入下式进行计算

$S_{XY}=1-\frac{6{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(p_i-q_i\right)}^2}}{N\left(N^2-1\right)}$ (14)

4.4.3. 结果分析

在常规测井解释中，孔隙度值与常规测井的电性参数AC、RT值有密切的联系，由于岩心样本采集成本较高，数量较少，直接用灰度值与岩心样本孔隙度建立关系难以准确的评价计算方法的可靠性，故可通过灰度值与其对应深度的AC、RT值的相关系数来对算法进行评价，不同间距间隔提取的灰度值与AC、RT值的相关系数见表1。其中最大值为0.77，最小值仅为0.25，与加权平均法、标准差法及算术平均值法相比，采用散点拟合法对对灰度值进行提取能取得较高的相关系数，研究结果表明散点拟合法在一定程度上有效的压制了图像采集时的噪声及异常值等影响，最大程度的还原了致密碳酸盐岩储层复杂结构的真实性。而在不同提取距离间隔上呈现不规律差异,不具有明显关系，也同时验证了该提取算法在设计上的可靠度。

Table 1. The influence of extraction distance interval on correlation coefficient in each gray value extraction method

表1. 各灰度值提取法中提取距离间隔对相关系数的影响

4.5. 孔隙度预测及应用实例

为进一步验证基于电成像测井图像孔隙度提取算法的实用性及其效果，基于MATLAB开发了该方法处理软件，在安装了相应版本MCRinstaller运行环境的计算机上，即可直接运行该程序。通过岩心归位，建立孔隙度与图像灰度值的线性关系表达式对孔隙度进行预测，最终实现从图像灰度值到孔隙度的提取。图6为E地区灯影组灯二上亚段地层常规测井孔隙度预测与灰度值孔隙度预对比。其中左图第6道为取心段实测孔隙度，7道为常规测井孔隙度解释成果，8道为通过处理软件提取的电成像灰度值，9道为用灰度值与实测孔隙度建立的线性表达式解释的孔隙度值。

Figure 6. Interpretation results of Logging porosity of Deng’er member of Dengying Formation in E area

图6. E地区灯影组灯二上亚段测井孔隙度解释成果图

通过对比可以看出，本文方法软件提取灰度值与实测孔隙度匹配程度良好，真实的还原了致密碳酸盐岩孔隙结构特征。在5434 m左右深度，灰度值异常下降以至孔隙度分布普遍偏高，通过薄片鉴定等手段，这主要是由于白云岩中含有少量泥粒和沥青所导致，对碳酸盐岩储层评价形象甚小。本文方法软件得到的解释成果在解释密度上有极大的提升，在解释效率上更加高效、精准，更有利于对致密碳酸盐岩储层进行评价工作。

5. 结束语

1) 本文研究用不同算法对灰度值进行提取，在各类提取算法中散点拟合法对灰度值进行提取能取得较高的相关系数，不同提取距离间隔上呈现不规律差异，不具有明显关系。

2) 通过对比常规测井孔隙度解释成果，本文章算法无论在精度和速度上都优于常规处理手段，更能反映地层孔隙结构的真实情况。

3) 研究表明，本文章算法对致密碳酸盐岩储层预测和评价具有指导意义，并具有显著的准确性及普及性，具有广阔的应用前景。