1. 相关理论和技术概念
深度学习的概念来自于对人工神经网络的研究,深度学习通过把通俗易懂的浅层特征串联起来表达更加深层的特征或属性,以此来探索数据本身的关联。深度学习目前正处于进步阶段,它的特点在于可以数据模拟分析,通过一个又一个的神经元节点进行计算最终得到结果。至今已经研发出多种多样的神经网络结构,为了能更好的预测雾霾天气情况,需要对现有的深度学习神经网络充分了解掌握,才能为实现深度学习预测雾霾提供理论支撑。因此,本章由浅入深依次讲述了基本神经网络、BP神经网络、循环神经网络和长短期记忆网络。
1.1. 基本神经网络(Basic Neural Network)
神经元是神经网络最基本的部分,一个神经元可以有多个输入端,每个输入端都有各自的权重,权重的大小则代表了这个输入端输入的信号的重要性,权重越大,输入信号越重要。神经元之间存在连接,输入的数据通过激活函数运算,输出一个带有偏置的输出,偏置代表被神经元控制的容易与否 [1]。神经元的基本结构如图1 所示。

Figure 1. Schematic diagram of neuron structure
图1. 神经元结构示意图
图中
是神经元的输入值;
是输入值所带的权重值,权重值的大小表示单元之间的连接强度,也决定了输入对输出的影响程度;b是偏置项,偏置项作为神经元的额外输入,它的值
始终为1,它的作用是确保即使输入值为0也能激活神经元。第一次运算过程为:
得到的值被激活函数处理,最终输出。
1.2. BP神经网络(BP Neural Network)
BP神经网络(back propagation neural network, BP)是一种以反向传播为主的多层前馈神经网络,它能够在传播途中通过自身的反馈调节上一时刻的输出数据,从而起到缩小误差的作用。当然,BP神经网络和其他神经网络一样也包含输入层、隐藏层和输出层。在神经元之间进行向前的信息传递过程中,激活函数发挥作用,计算出误差的值,如果误差值太大的话,神经元之间便进行向后的反向传播,所以此神经网络的运行方法就是数据按正向传播,误差按方向传播,在此过程中不断修改阈值与权重,直到将损失函数降为最小,得到最接近的期望值。
反向传播主要用到梯度下降的方法,函数在正方向上变化的最快,对数据求导可以得到它的偏导数,如果偏导数大于零则进行反向传播,如果偏导数小于零则继续进行正向传播。图2是BP神经网络的结构图。

Figure 2. Structure of BP neural network
图2. BP神经网络结构
从图中可以看出,BP网络是一个三层结构,即输入层、隐含层和输出层,隐含层可以只是一层也可以有很多层 [2],这取决于自己的设定,若隐含层数较多,则训练过程缓慢,输出结果更加准确。神经元的个数取决于输入端的多少,数据从前向后依次进入各层中进行处理,最后从输出层输出 [3]。
1.3. 循环神经网络(Recurrent Neural Network, RNN)
循环神经网络(Recurrent Neural Network, RNN)善于循环往复地处理一段有时间关联的数据,它和其他神经网络不同,虽然都有输入层、隐藏层和输出层,但RNN各层之间并非没有反馈联系,这就使得RNN优于其他传统神经网络,它可以持续保留信息并且能在短时间内记忆信息,将很久之前的信息调出并与现有的信息结合形成对未来的预测,提高了预测的准确性。
循环神经网络内部的隐藏层各层神经元之间通过链接循环传递信息,同层神经元之间没有链接,也不可跨层链接,所以上一时刻神经元的输出数据和这一时刻神经元的输入数据共同组成了此时刻地输入,也就是说RNN可以随时调用之前的信息,但是由于跨度太大,过久地信息储存的不是很好。
循环神经网络最明显的特性就是具有时序性,专门用于处理具有时间序列特性的数据,挖掘输入数据的序列特点以及信息之间的关联,因此常用来实现回归预测。图3为RNN地结构图。
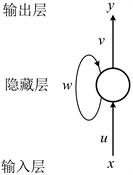
Figure 3. Typical structure diagram of recurrent neural network
图3. 循环神经网络典型结构图
从图中可以看出,RNN地内部隐藏层中有一个自循环,历史信息被反复传递,之前时刻地信息和新的输入数据一起参与正向传播,故而在接下来的每一次训练中,都会被此前所有时刻影响,而之前的所有信息都会被保留。
对于进行到t时刻的神经元节点,它的输入记作x,输出记作y,输入权重记作u,输出权重记作v,隐藏层的权重记作w。在神经元不断被循环往复计算时,隐藏层读取输入层的输入数据x,并输出一个数据y,同时隐藏层的状态值会从t时刻传递到t + 1时刻,也就是说隐藏层的输入不光包含输入层的输入数据,还包含上一时刻隐藏层的输出 [4]。
当然,对于一段确定时间序列长度的循环神经网络,本文可以对它内部进行展开,如图4所示。
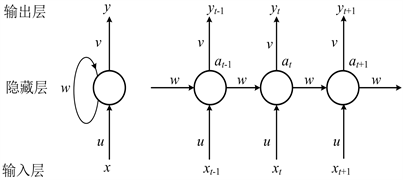
Figure 4. Unfolding diagram of cyclic neural network structure
图4. 循环神经网络结构展开图
从图4中可以得到,对于t刻,输入层输入的数据可以记为
,输出层输出的数据记为
,隐藏层的输出数据记为
,u是输入权重,v是输出权重,w是隐藏层权重。RNN可以进行前向和反向传播,前者的传播过程如式
和
所示。
,
为激活函数,
,
为偏置项。从公式中可以看到,输出值包含了当前时刻的值,而当前时刻的值又包含了上一时刻的值,所以随着时序的增加,以前的信息占所有信息的比重会减小,最终随着新输入的增加而逐渐消失,这就是循环神经网络的弊病即梯度消失或梯度爆炸问题 [5]。这个问题产生的原因是由于链式法则的运算特性,在反向传播时,权重不断地加入计算,逐渐变小直至趋于零,最终导致权重不能更新,形成局部最优解的情况。
1.4. 长短时记忆网络(Long Short-Term Memory Network)
长短时记忆网络(Long Short-Term Memory Networks, LSTM)的问世充分解决了RNN存在的问题,它是一种全新的模型结构,是一种为了解决循环神经网络梯度消失或梯度爆炸问题而研究出的新型神经网络 [6],它与RNN结构相似,区别在于在隐藏层中添加了一个记忆细胞,使其能够和之前时刻产生联系,判断信息的可用性,去除掉一部分不可用的信息,输出可用信息。并且在每个神经元中加入了三个门,分别为输入门、遗忘门和控制门,这三个门分工不同,发挥的作用也各不相同。图5为LSTM神经元的结构。
如图所示的三个模块为部分LSTM神经元结构,每一个模块为不同时刻神经元。从输入端接收数据并开始计算的过程。对于t时刻,
为上一个神经元细胞输出的信息,
为上一时刻传出的数据。xt为当前时刻输入的数据。经过三个门的运算。细胞信息ct进行一次更新,并输出当前时刻的输出数据at。由此可见,t时刻的输入和上一时神经元细胞隐藏层的输出共同作为t时刻的输入。
在一段固定长度的时间序列中,神经元内部三个“门”一起控制开断,门其实就是通过激活函数来对输入信息进行控制的结构,而通常激活函数选用sigmoid函数,由于sigmoid函数的值域为(0, 1),当门处于开通状态时,输出为1,则表示信息可以通过;当门处于关闭状态时,输出为0,则表示信息不能通过。
记忆细胞类似于一条传送带,贯穿了整个时间序列,这其中只和其他部分有一些少量的交互,从开始时刻到目前为止所有的信息都可以被LSTM的记忆细胞记住然后传递给下一时刻,通过三个门的作用任意调取。这便是LSTM优于RNN的地方。图6为LSTM神经元记忆细胞结构。

Figure 6. LSTM neuron memory cell structure
图6. LSTM神经元记忆细胞结构
下面分别介绍输入门、遗忘门和输出门的结构特点和运算机制:
1) 遗忘门
遗忘门的作用是丢失没用的信息,将有用的信息保留下来,通过遗忘门可以对历史信息进行选择性处理,其结构如图7所示。
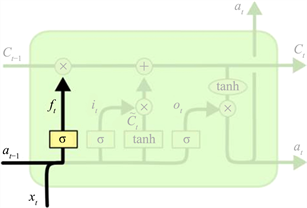
Figure 7. LSTM neuron forget gate structure
图7. LSTM神经元遗忘门结构
从图中可以看到,遗忘门的输入由上一时刻的输出和此时刻的输入组成,计算公式如式所示:
其中,
为上一时刻的输出数据,
为当前时刻的输入数据,
为当前时刻的输出,
是偏置项,
是权重,σ是激活函数。遗忘门通过这个激活函数将上一时刻的输出值和当前时刻的输入值进行运算得到一个在(0, 1)之间的值 [7],这个值可以视为一个比例,然后用这个比例与上一时刻的单元状态进行点乘,从而实现筛选的目的,即丢弃无用信息,保留有用信息。
2) 输入门
输入门是用来决定加入多少信息的控制开关,也就是决定有多少信息进入当前时刻的记忆细胞,其结构如图8所示。
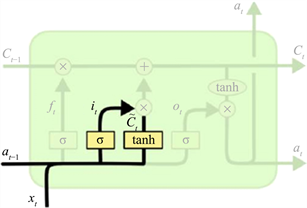
Figure 8. LSTM neuron input gate structure
图8. LSTM神经元输入门结构
它的计算公式为:
其中,
为上一时刻的输出数据,
为当前时刻的输入数据,
为当前时刻的输出,
是偏置项,
是权重,初始值为(−1, 1)。这里包含两个步骤,第一步是通过σ函数将数值控制在(0, 1)之间,第二步是由一个tanh函数生成当前输入的单元状态。其中“1”表示允许通过,“0”表示不允许。新计算出的值
为遗忘门筛选的历史信息和输入门选择输入的信息,这些信息被加入到状态中,完成细胞状态更新。
3) 输出门
输出门的作用是选择什么样的信息能被输出,然后流进下一细胞,其结构如图9所示。
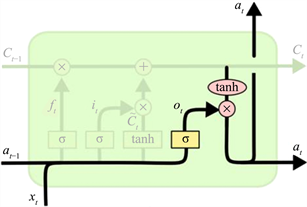
Figure 9. LSTM neuron output gate structure
图9. LSTM神经元输出门结构
从图中可以看出,sigmoid函数决定了哪些信息可以被输出,如果当前状态值为1,则表示输出,如果状态值为0,则不输出。然后与经过tanh函数处理过的信息进行相乘,然后输出需要被输出的信息。
其计算公式为:
输出信息为:
以上便是LSTM神经网络的介绍,综上所述,LSTM在保留循环神经网络优点的基础上,加入了记忆细胞和“三门”结构,能完全保留历史信息中有用的部分,更加直接便捷地调取拟合具有时间序列特性的数据,有效地防止了梯度消失和梯度爆炸,避免了训练过程中发生的不必要的问题。正因LSTM的优越性,在语音识别、图像处理和预测数据等领域中LSTM被广泛应用,并取得了不错的成果 [8]。
1.5. 基于AM的神经网络(Neural Network Based on AM)
1.5.1. 注意力机制
注意力机制(Attention Mechanism, AM)是模仿人脑的一种运行机制,也是一种深度学习的方式,通过这种方式模型可以锁定特定的信息,自动忽略不重要的信息,分辨出哪些是有用的信息。注意力机制会对输入数据进行特征性分析,赋予每一个向量对应的权重值,这些对预测结果影响较大的信息就会被凸显出来,因此,带有注意力机制的神经网络模型可以挖掘出与预测目标关系最为密切的输入信息,对预测结果产生很大影响。
它最核心的操作就是一串权重参数,要从序列中学习到每一个元素的重要程度,然后按重要程度将元素合并。权重参数就是一个注意力分配的系数,决定给哪个元素分配多少注意力。
图10为基于注意力机制的神经网络的结构图。
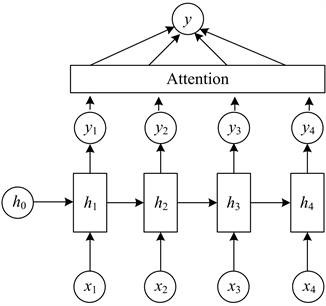
Figure 10. Neural network based on attention mechanism
图10. 基于注意力机制的神经网络结构图
1.5.2. 基于AM的网络结构
从前文可知在神经网络中加入LSTM神经元可以记忆较长序列的信息,并且保留重要信息遗忘不重要信息,而加入Attention层的作用是突出重要信息对预测结果的影响。
1) 引入注意力机制的神经网络模型内部含有两层神经元,并且在两层神经元中使用Dropout层进行连接以减少训练时参数量和防止过拟合。Attntion机制引入权重系数。对雾霾及其影响因子在前一个神经元层与后一个神经元层进行数据特征提出时的输出权重比例进行自适应地重新分配再加权,即自动捕获城市雾霾预测时间序列的自身变化性和周期性。
2) 多次使用Attention机制对多个神经元进行计算,输入信息首先经过第一层神经元,经过运算信息会被输送到第二层神经元,接下来进入Attention层进行学习,最终输出一个一维向量。
2. 基于LSTM算法的雾霾天气预测
本章通过把某城市2018年1月1日至2018年12月31日的空气污染物因素和空气质量指数当作输入数据,使用MATLAB搭建基于LSTM神经网络的雾霾天气预测模型,从而对某市2019年1月的PM2.5浓度进行预测研究。为了准确预测出PM2.5浓度,以某市2018年气象数据为例,引入前文提到的LSTM模型,构建神经网络,建立多输入、单输出的关系进行预测。
2.1. 数据处理(Data Processing)
将收集到2018年1月1日~2018年12月31日逐日PM2.5、PM10、SO2、CO、NO2、O3_8h、AQI浓度值作为数据集,数据共计2555条,划分为训练集和测试集 [9]。前80%的数据作为训练集,后20%的数据作为测试集。将2019年1月1日至2019年1月31日逐日PM2.5、PM10、SO2、CO、NO2、O3_8h、AQI浓度值作为预测集,数据共计217条。所有数据均经过差值补全和归一化处理输入到模型中。图11为收集到的部分原始数据展示。
2.2. LSTM神经网络模型设计(Design of LSTM Neural Network Model)
本文第三章讲述了利用BP神经网络模型进行预测雾霾浓度,但由于雾霾预测受多种因素的影响,普通的BP模型不能全面考虑到时间和空间上的影响因子,而且对于多源大数据不能充分利用这一点造成预测结果不准确,模型的自适应性还有待提高。因此,本章节重点在LSTM模型上进行预测PM2.5浓度预测,利用数据的相关联系,改善了输入数据的质量,从而提高预测准确度。
本章搭建了LSTM模型作用于预测PM2.5浓度,其预测步骤大致如下图12所示。
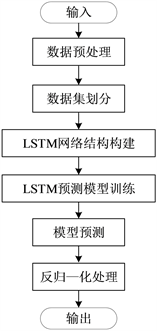
Figure 12. Flow chart of LSTM model prediction
图12. LSTM模型预测流程图
2.2.1. 激活函数
神经网络中有一个必不可少的部分那就是激活函数,常常选用非线性激活函数作为运算法则,用来解决非线性问题,它可以将值缩小至较小的范围内。在激活函数没有起作用之前得出的输出值0或1,也可能是值域为(0, 1),常常通过使用0和1来代表是或否,加上一个激活函数就可以实现这一功能,如果大于0,则输出1,如果小于0,则输出0。常见的几种激活函数有ReLU,Lsaky Relu,TanH和Sigmoid,它们的图像如图13所示。
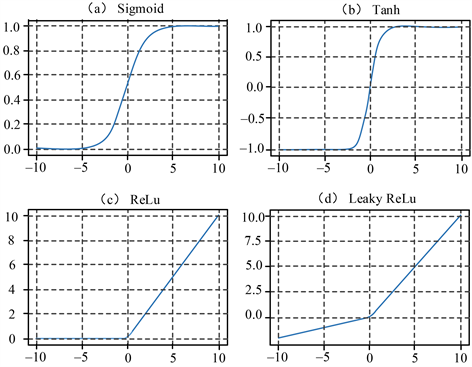
Figure 13. Four common activation function images
图13. 四种常见的激活函数图像
由于LSTM神经元有三个门,而信息是通过一个激活函数才能进入神经元中,所以本文需要一个能控制门的关断的激活函数。sigmoid函数的值域为(0, 1),正好适合本文的神经网络,故而激活函数为sigmoid函数。在本文第二章简单介绍了一些比较普遍激活函数,在此本文选取两种在LSTM神经网络中用到的激活函数做出详细说明。
1) Sigmoid函数
Sigmoid函数在x轴范围内不管取何值,y轴对应的因变量都是在0到1范围内的,它的函数图像如图14所示。
计算公式为式为:
这个函数是一个非线性的,当输入值趋近于负无穷时,输出值趋近于0;当输入值趋近于正无穷时,输出值趋近于1,所以三个门都采用这个函数来表示门的关断。
2) Tanh函数
Tanh函数在x轴范围内不管取何值,y轴对应的因变量都是在−1到1范围内的,它的函数图像如图15所示。
计算公式:
与sigmoid函数不同的是,tanh函数输出的值为零均值,当自变量x趋近于负无穷或者正无穷时,函数的导数趋近于零。
2.2.2. 损失函数
损失函数用来描述预测值与实际值的差距,也叫作目标函数,是本文要优化的目标。损失函数被用来判别一个模型的预测与期望之间拟合程度的大小,也就是说,如果损失函数小的话,这个模型预测的就较为准确,反之则效果不好,为了得到结果较好的模型,需要对其参数进行详细地设置,缩小损失函数。
本文主要用到均方根误差损失函数,公式为
其中
为预测获得的结果,n是训练集的样本个数,
即损失函数。同理,均方根差越大则代表训练结果的误差越大,均方根差越小代表训练结果越接近真实值。
2.2.3. 优化器
深度学习常常需要大量的时间和计算资源进行训练,优化器作为神经网络训练时所用到的必不可少的一种工具,它的作用是压缩训练时间、减少资源占用、调整参数,从而达到减小误差的目的,使得神经网络充分发挥性能。常见的优化器为随机梯度下降(SGD)、Momentum、Adagrad、Adadelta、RMSprop和Adam。
SGD算法在很早以前就被开发出来,被应用到深度学习领域里,这是一种较为普遍的算法,它的原理是寻找出一个损失函数行进的负梯度方向,这个方向上损失函数减少的速率最快。
随机梯度下降算法(SGD)可以求出目标函数的最小值,而且由于每次迭代,只计算一个样本,效率比较高。除此之外,在面对非凸函数时,存在局部最小值,SGD可以快速地筛选出最小的数据。
然而随机梯度下降法也存在一些弊端,如果将学习率定义的太小的话,训练过程就会减慢,如果将学习率定义的过大的话,训练的时间就会缩短,这可能导致预测的结果不准确,或者损失函数会在极小值处来回波动,而且需要不停调整学习率。
因此,本次实验主要使用Adam算法作为神经网络的优化器,它结合了Momentum和RMSprop的优点,这也是近几年来使用最多的一种优化器,其训练效果可想而知。它的优点在于,可以自适应学习率,依据情况改变学习率,提高学习速度,减少内存占用,不需要更好的硬件就能完成训练。
2.2.4. 防止过拟合的方法
过拟合是指将误差也进行拟合,造成预测不理想,与实际值出现较大偏差,在训练过程中如果输入的数据太少或者训练的时间过长都会产生这种现象,本文所采取的解决办法是Dropout,这个方法是正则化的一种。在训练过程中,每次迭代都会随机删除一些神经元,保留剩下的神经元,然后再进行训练,这样可以避免出现过拟合的现象。
在深度学习过程中,会出现过拟合和欠拟合的现象。欠拟合是指在训练网络的过程中,没有发现适合目标问题的参数,在训练数据和验证数据中诱发模型的高错误。所谓过拟合,特别是在网络训练过程中,为了让模型和训练数据变得非常合适,训练数据学习太多,在训练数据中,模型的准确度较高,测试数据准确度较低。处理目前不合适的问题的三种一般的接触方式是增加训练组的数据量,让模型可以用更多的数据进行学习和训练。对于过拟合问题,这篇文章为了防止过拟合,选择了Dropout方法。
3. 实验分析(Experimental Analysis)
3.1. 参数设置
LSTM预测模型的网络结构和参数设置如下:
1) 输入层神经元个数:由于LSTM的特性,所以输入层神经元个数就是输入数据的个数为1;
2) 输出层神经元个数:输出层为全连接层,由于本次预测模型为多输入单输出模型,所以输出层节点个数是输出层维度为1;
3) 隐藏层的数量:隐藏层神经元的数量直接影响了模型的训练时间和预测准确度,由于LSTM网络内部存在记忆细胞和三门结构,过多的隐藏层也会导致系统运算消耗更多的时间和资源,这样往往适得其反,因此需要通过试错法找出最佳隐藏层数量,经过试验确定了隐藏层数量为200;
4) 激活函数:由前文分析可得激活函数默认设置为sigmiod函数和tanh函数;
5) 损失函数:RMSE函数作为模型的损失函数即均方根误差函数;
6) 初始学习率:使用试错法将学习率设置为0.0005;
7) 迭代次数:通过试错法将迭代次数设置为100,200,300,400,500,实验结果当迭代次数为200时效果最好;
8) 为了防止梯度爆炸,将梯度阈值设置为1 [10];
9) 将输出的数据与测试数据进行反向归一化进行对比,通过计算测试值与实际值的误差指标,评价模型预测能力,最后得出PM2.5预测的值。
3.2. 基于LSTM模型的雾霾浓度预测结果与分析
图16表示LSTM神经网络模型的训练过程,上面为均方根误差,下面为损失程度,从图中可以看出,训练在开始时图像有一个很大的波动,随后趋于平缓,均方根差逐渐趋近于为零,损失程度也逐渐降为零。虽然误差仍然存在,可能因为某种不可控因素而导致波动,却也在接受范围之内,整体来看表现良好,由此看来该模型可以用作雾霾预测。
1) 对测试集的预测。首先2018年的数据前80%作为训练集,后20%作为测试集,进行一次对测试集的预测 [11]。图17、图18和图19分别为误差直方图、误差针状图和预测值与实际值的拟合情况:
从左边的直方图可以看出,误差在区间(−10, 15)内最大,随后逐渐降低。右边为针状图,描述每个时间点的误差情况。并且可以看到,均方根误差为8.578,虽然有小部分误差,但是在可接受范围内,由此可以说明此模型具有良好的训练效果。
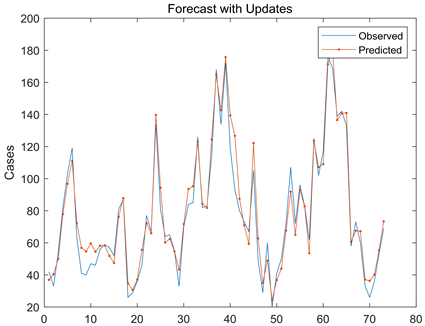
Figure 19. The fit between the predicted value and the actual value
图19. 预测值与实际值拟合情况
从图19中可以看出,对于测试集的预测,实际值与预测值大致相符,两条曲线基本重合,只有在少部分区间内有误差,整体来看预测效果不错,表明了基于LSTM算法的预测模型可以用于PM2.5的预测。
2) 对预测集的预测。用2019年1月1日至2019年1月31日的空气污染物数据作为预测集,
图20为预测情况,从图中可以看出,实际值与预测值大致相符,虽然存在误差,但总体效果还是较好的。验证表明,LSTM模型对城市雾霾的预测具良好的效果,但不是十分准确,在某时刻存在一定误差。
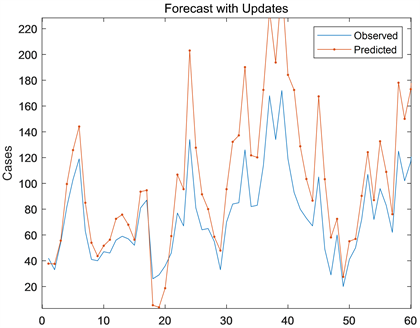
Figure 20. Fitting effect between predicted value and actual value
图20. 预测值与实际值拟合效果
4. 总结与展望
4.1. 总结
随着城市工业化的发展,雾霾成为当今社会影响人们健康的罪魁祸首之一,因此,治霾防霾就显得尤为重要。本文主要通过对大气污染物以及气象要素等一系列具有时间序列特性的数据进行分析处理,找出与PM2.5浓度相关性最大的影响因素,利用LSTM和AMLSTM训练,预测出未来一段时间内PM2.5的浓度,并对两种神经网络预测的准确性进行对比。
4.2. 展望
大数据时代下深度学习技术的发展越来越成熟,人们对城市雾霾预测的需求也越来越高。在本文研究基础上,值得进一步开展的工作如下:
1) 基于多源数据融合的深度学习城市雾霾预测方法,除了本文所选取的时间和空间因素之外,还应该将工业化作业、人口密度、交通流量、多城市路网等多种影响因子纳入预测模型的辅助特征,实现多个领域的叠加影响,从而实现城市雾霾的预测;
2) 本文所构建的城市雾霾预测模型的预测时间域不宽,为进一步满足社会需要,后续将通过设计如滑动窗口等相关研究工作来对模型进行改进,使其能实现更长时间的城市雾霾预测。
NOTES
*第一作者。
#通讯作者