基于多项式插值的有限差分法求解Helmholtz方程声硬散射体散射问题

Finite Difference Method Based on Polynomial Interpolation for Solving Hard Acoustic Scattering Problems of the Helmholtz Equation

摘要: 有限差分公式在无网格方法求解微分方程数值解中起着重要作用。本文针对Helmholtz方程的声硬散射体散射问题，通过多项式插值来创建有限差分公式。本文运用一种简单实用的节点分布，既保证多元多项式插值的唯一可解性，又使矩阵为三角矩阵，以便构造的基本多项式化为Lagrange基多项式。最后给出了Helmholtz方程Neumann问题的数值算例。

Abstract: The finite difference formula plays an important role in solving the numerical solution of differential equations by the meshless method. In this paper, the finite difference formula is created by polynomial interpolation for the scattering problem of acoustic hard scatterers of the Helmholtz equation. We use a simple and practical node distribution, which not only ensures the unique solvability of multivariate polynomial interpolation, but also makes the matrix a triangular matrix, so that the basic polynomial constructed can be transformed into Lagrange basis polynomial. Finally, we give the numerical example of the Neumann problem of the Helmholtz equation.

1. 引言

无网格法是计算力学领域较活跃的研究分支之一。无网格法的近似函数是建立在一系列离散点上的，不需要借助于网格，克服了有限元法对网格的依赖性，在涉及网格畸变、网格移动等问题中显示出明显的优势，同时无网格法的前处理过程也比有限元法更为简单 [1]。

由于无网格法回避了有限元计算中网格畸变带来的困难，并且容易局部地嵌入多种计算模型。无网格法的创立与发展对于求解传统的有限元法、有限差分法等无法解决的问题有重要的意义与应用价值。

与有限元法不同，无网格法中使用的近似函数大都不具有插值特性，因此在基于Galerkin法的无网格法中处理本质边界条件具有一定的困难。张雄 [2] 等都对本质边界条件的处理进行了深入研究，提出了直接配点法、拉格朗日乘子法、修正变分原理、罚函数法、位移约束方程法等。目前在无网格法中使用的近似函数主要有：核函数近似、重构核近似、最小二乘近似、单位分解函数和径向基函数等 [3]。

本文主要是基于黄小为和吴传生求解Laplace方程以及热传导方程的工作 [4]，以及Gasca和Maeztu的工作 [5]，以Helmholtz方程为例，求解声硬散射体散射问题。

声波的散射是指入射波在传播过程中由于介质的非一致性从而产生波的传播方向发生偏离的现象。引起散射现象的物质称为散射体，根据散射体的不同性质可分为障碍散射、介质散射等。声波的正散射问题指的是已知入射场和散射体的信息，求解散射场或远场。一般的，我们假定声波是时谐的。正散射问题即是在无界域上求解具有一定边界条件和辐射条件的Helmholtz方程或Maxwell方程组的定解问题 [6]。

在实际生活中，散射现象普遍存在，比如山谷回音。声波和电磁波的散射问题的研宄在许多领域有重要的应用价值，如卫星勘探、雷达目标识别、量子力学、工业制造、无损检测、医疗成像和地质勘探等等 [7] [8] [9] [10]。

本文结构如下：在第一节提出了一个简单且实用的节点分布并确定插值节点集；在第二节构造有限差分公式；在第三节给出Helmholtz方程Neumann问题的数值算例；第四节针对算例做误差分析。

2. 节点分布和插值节点集

2.1. 节点分布

对于二维平面问题，如果节点分布在一系列平行直线上，依据多项式插值相关理论，若依次在直线 $l_i$ 上选取 $n-i+1$ 个节点， $i=0,1,\cdots ,n$，关于这 $C_{n+2}^2$ 个节点构成的插值节点集，次数不超过n的二元多项式插值问题是唯一可解的。而且，关于此插值节点集，通过局部多项式插值法构造广义有限差分公式，其权系数确定有简单的迭代算法。因此，生成简单的平行直线节点分布，将区域中的离散节点位于一系列的平行直线上，可方便地选取出局部插值节点集来求解多项式插值问题。

基于上述描述，为方便地确定插值节点集和构造插值多项式，本文我们生成平行直线型的节点，以Helmholtz方程为例，求解Neumann问题。

在二维有界连通区域 $\Omega \subset R^2$ 上，用 $\Delta$ 表示平面区域的离散化级别。离散化级别会决定方程是否病态，进一步影响方程解的稳定性。我们假设 $\Omega =\left\{\left(x,y\right)|a_1\le x\le a_2,g_1\left(x\right)\le y\le g_2\left(x\right)\right\}$，其中 $a_1=\inf \left\{x|\left(x,y\right)\in \Omega \right\}$， $a_2=\sup \left\{x|\left(x,y\right)\in \Omega \right\}$。

首先确定区域 $\Omega$ 在投影x轴上的节点数

$I=\{\begin{array}{l}1,a_1=a_2,\\ 2,0<a_2-a_1<\Delta ,\\ \left[\frac{a_2-a_1}{\Delta }\right]+1,a_2-a_1\ge \Delta ;\end{array}$

并在投影间隔上生成等距节点

$x_i=\{\begin{array}{l}{a}_1,I=1,\\ a_1+\frac{a_2-a_1}{I-1}\left(i-1\right),I>1,\end{array}i=1,\cdots ,I.$

类似的，我们生成一系列通过这些节点并平行于y轴的直线，并在直线和 $\Omega$ 上生成等距节点：

$J_i=\{\begin{array}{l}1,b_{i1}=b_{i2},\\ 2,0<b_{i2}-b_{i1}<\Delta ,\\ \left[\frac{b_{i2}-b_{i1}}{\Delta }\right]+1,b_{i2}-b_{i1}\ge \Delta ,\end{array}i=1,\cdots ,I;$

$y_{ij}=\{\begin{array}{l}{b}_{i1},J_i=1,\\ b_{i1}+\frac{b_{i2}-b_{i1}}{J_i-1}\left(j-1\right),J_i>1,\end{array}j=1,\cdots ,J_i.$

其中 $b_{i1}=\inf \left\{y|\left(x_i,y\right)\in \Omega \right\}$， $b_{i2}=\sup \left\{y|\left(x_i,y\right)\in \Omega \right\}$。

最终，生成区域 $\Omega \subset R^2$ 上节点

$T={\displaystyle \underset{i=1}{\overset{I}{\cup }}\left\{\left(x_i,y_{ij}\right)|j=1,\cdots ,J_i\right\}.}$

2.2. 插值节点集

本文采用广义有限差分法来求解方程，该方法本质上是以计算点附近的相邻节点的函数值的线性组合去逼近计算点处的导数。因此，我们先要选取计算点附近的相邻节点集。

对于移动最小二乘法和径向基函数插值法，通常是给定节点数目，选择与计算点最邻近的节点；或是给定邻域半径，选择以计算点为中心的邻域内的节点。这种选取节点集的做法都是非常简单直接而且有快速的算法。节点集选取面临的最大问题是可能会导致奇异性。为避免奇异性问题，我们基于多元多项式插值来构造广义有限差分法。

在获得区域 $\Omega$ 的平行直线型(平面–直线型)节点分布T后，对于给定的点 $p\in \Omega$ 和多项式次数 $n\in N$，我们在节点p附近选取插值节点集 ${\chi }_n\left(p\right)$。

令 $T=\left\{\left(x_i,y_{ij}\right)|i=1,\cdots ,I;j=1,\cdots ,J_i;I\ge n+1\right\}\subset \Omega$ 为确定的平行直线型节点集，在该点集中选取与点p距离最近的 $n+1$ 个点，构成新的点集 ${\rho }_0\left(p\right)$。

在2.1节中，生成了节点 $T=\left\{\left(x_i,y_{ij}\right)|i=1,\cdots ,I;j=1,\cdots ,J_i\right\}\subset \Omega$，然后将 ${\left\{J_i\right\}}_{i=1}^I$ 降序排列为

$J_{m_1}\ge J_{m_2}\ge \cdots \ge J_{m_I}.$

为了保证 ${\chi }_n\left(p\right)$ 存在，让 $\Delta >0$ 为足够小的常数，使得 $I\ge n+1$ 并且

$J_{m_k}\ge n+2-k,k=1,\cdots ,n+1.$

为确定插值节点集，给定降序排列 $r=n+1,n,\cdots ,1$，先令集合 $S=\left\{1,\cdots ,I\right\}$，后构造 $V=\left\{i\in S|J_i\ge r\right\}$，然后通过下述规则迭代

$k\left(i\right)=\underset{1\le l\le J_i-r+1}{\arg \min }\left|v-\frac{y_{i,l}+y_{i,l+r-1}}{2}\right|,i\in V;$

$i_r=\underset{i\in V}{\arg \min }\left({\left(u-x_i\right)}^2+{\left(v-\frac{y_{i,k\left(i\right)}+y_{i,k\left(i\right)+r-1}}{2}\right)}^2\right);$

${\rho }_r\left(p\right)=\left\{\left(u_{i_r},v_{i_r,s}\right)|s=k\left(i_r\right),\cdots ,k\left(i_r\right)+r-1\right\};$

$S=S\backslash \left\{i_r\right\}.$

最终获得插值节点集

${\chi }_n\left(p\right)={\displaystyle \underset{r=1}{\overset{n+1}{\cup }}{\rho }_r\left(p\right)}=\left\{\left(u_r,v_{rs}\right)|\left(r,s\right)\in I_n^2\right\}\subseteq T.$

3. 有限差分公式

用某点附近点的函数值的线性组合去逼近函数在该点处的导数，导出的公式称为广义有限差分公式。

给定函数 $f:{ℝ}^d\to ℝ$， ${\chi }_n\left(p\right)=\left\{q_{\alpha }|\alpha \in I_n^d\right\}$ 为在点p附近选取的插值节点集，在 ${\Pi }_n^d$ 上关于 ${\chi }_n\left(p\right)$ 的多项式插值问题是唯一可解的。f关于 ${\chi }_n\left(p\right)$ 的Lagrange插值多项式为

${\displaystyle \underset{\alpha \in I_n^d}{\sum }f\left(q_{\alpha }\right)l_{\alpha }}\left(x\right),x\in {ℝ}^d.$ (1)

其中， ${\left\{l_{\alpha }\left(x\right)\right\}}_{\alpha \in I_n^d}$ 为Lagrange基函数。

可以将Lagrange插值多项式看作是函数f的一种逼近，该多项式在点p处的导数作为f在点p处的导数的近似值。我们对(1)式求导，再将x取作p，可以得到f在点p处的导数的广义差分公式：

$f^{\left(\gamma \right)}\left(p\right)\approx {\displaystyle \underset{\alpha \in I_n^d}{\sum }f\left(q_{\alpha }\right)D^{\gamma }{l}_{\alpha }}\left(x\right).$ (2)

其中， $\gamma \in \mathbb{N},\left|\gamma \right|\le n$。 $D^{\gamma }{l}_{\alpha }\left(x\right)$ 是 ${\left\{l_{\alpha }\left(x\right)\right\}}_{\alpha \in I_n^d}$ 的导数，可称为权系数，记作 ${\omega }^{\alpha }$。因此(2)式可写为：

$f^{\left(\gamma \right)}\left(p\right)\approx {\displaystyle \underset{\alpha \in I_n^d}{\sum }f}\left(q_{\alpha }\right){\omega }^{\alpha }.$ (3)

为简便起见，本文针对二元情形，考虑点p选取的插值节点集为平行直线型节点，推导出二元广义有限差分格式，再在数值实验部分展示具体的应用。

设点p选取的插值节点集为平行直线型节点 ${\chi }_n\left(p\right)=\left\{\left(u_i,v_{ij}\right)|\left(i,j\right)\in I_n^2\right\}$，插值节点位于一系列平行于y轴的直线上，依据(3)式得到相应的广义差分公式：

$f^{\left(\gamma \right)}\left(x_0,y_0\right)\approx {\displaystyle \underset{\left(i,j\right)\in I_n^2}{\sum }f\left(u_i,v_{ij}\right){\omega }_{ij}}.$ (4)

其中，权系数 ${\omega }_{ij}=D^{\gamma }{l}_{ij}\left(x_0,y_0\right)$。

通过一元Newton基函数 ${\left\{{\xi }_i\left(x\right)\right\}}_{i=1}^n$ 与一元Lagrange基函数 ${\left\{l_j^i\left(y\right)\right\}}_{j=0}^{n-i}$，确定出二元Lagrange基函数 ${\left\{l_{ij}\left(x,y\right)\right\}}_{\left(i,j\right)\in I_n^2}$ ：

$\{\begin{array}{l}{l}_{n0}={\xi }_n\left(x\right)l_0^n\left(y\right),\\ l_{ij}={\xi }_i\left(x\right)l_j^i\left(y\right)-{\displaystyle \underset{\begin{array}{c}\left(r,s\right)\in I_n^2\\ r>i\end{array}}{\sum }{\xi }_i\left(u_r\right)l_j^i\left(v_{rs}\right)l_{rs},}\end{array}$

其中 $i=0,\cdots ,n-1;j\in I_{n-i}^1$。则权系数 ${\omega }_{ij}$ 也能被确定出来：

$\{\begin{array}{l}{\omega }_{n0}={\xi }_n^{\left({\gamma }_1\right)}\left(x_0\right)l_0^{n\left({\gamma }_2\right)}\left(y_0\right),\\ {\omega }_{ij}={\xi }_i^{\left({\gamma }_1\right)}\left(x_0\right)l_j^{i\left({\gamma }_2\right)}\left(y_0\right)-{\displaystyle \underset{\begin{array}{c}\left(r,s\right)\in I_n^2\\ r>i\end{array}}{\sum }{\omega }_{rs}{\xi }_i\left(u_r\right)l_j^i}\left(v_{rs}\right),\end{array}$

其中 $i=0,\cdots ,n-1;j\in I_{n-i}^1$。

4. 数值实验

本文以Helmholtz方程为例，求解Neumann问题。本文选取的方程为：

$\{\begin{array}{l}{\nabla }^{2}u+ku=0,\text{in}\Omega ,\\ \frac{\partial u}{\partial n}=g,\text{on}\Gamma \text{.}\end{array}$ (5)

其中 $\Omega =\left\{\left(x,y\right)|-1\le x\le 1,\sqrt{1-x^2}\le y\le 2\right\}$， $\Gamma =\partial \Omega$， $k=2$， $g=-x\cos x\cos y-y\sin x\sin y$。已知该问题的解析解是 $u=\sin x\cos y$。

$T=T_0\cup T_1$ 为用上述方法确定的节点集合， $T_0$ 为内部节点集合， $T_1$ 为边界节点集合。将节点代入下式

$\{\begin{array}{l}{\nabla }^{2}u\left(x_i\right)+ku\left(x_i\right)=0,\text{in}\Omega ,\\ {\frac{\partial u}{\partial n}|}_{x_i}=g\left(x_i\right),\text{on}\Gamma \text{.}\end{array}$ (6)

式(6)中 ${\nabla }^{2}u\left(x_i\right)$ 及 ${\frac{\partial u}{\partial n}|}_{x_i}$ 用广义有限差分公式替换，节点按内部节点、边界节点的顺序排列，写成矩阵方程的形式即可得：

$\left(\begin{array}{c}L+kE\\ B\end{array}\right)\left(\begin{array}{c}{u}_0\\ u_1\end{array}\right)=\left(\begin{array}{c}0\\ g\end{array}\right).$ (7)

式(7)中，Laplacian算子微分矩阵 $L_{N_0\times N}=\left(L_0,L_1\right)$ 及 $\Gamma$ 上边界算子微分矩阵 $B_{N_1\times N}=\left(B_0,B_1\right)$ 按内部节点，边界节点划分为两块。

$N_0$ 为内部节点数， $N_1$ 为边界节点数， $N=N_0+N_1$。g是g在边界 $\Gamma$ 上的边界节点处的函数值组成的向量。 $u_0,u_1$ 分别为对应于内部节点、边界节点的未知向量。

式(7)可简化为 $N_0+N_1$ 个方程、 $N_0+N_1$ 个未知量的线性方程组：

$\left(\begin{array}{cc}{L}_0& L_1\\ B_0& B_1\end{array}\right)\left(\begin{array}{c}{u}_0\\ u_1\end{array}\right)=\left(\begin{array}{c}0\\ g\end{array}\right)-\left(\begin{array}{c}kE\\ 0\end{array}\right)\left(\begin{array}{c}{u}_0\\ u_1\end{array}\right).$ (8)

通过求解(8)获得函数u在内部节点以及边界节点处的函数值。

4.1. 确定参数值

为确定节点分布，我们需要确定 $\Delta$ 和n两个参数。先假定这两个参数的值，求出对应的数值解，再对比数值解与解析解。依据这两个解的最大绝对误差Err0和平均绝对误差Err1确定出较好的选取值。

$\Delta$ 的候选值有 $\frac{1}{10}$， $\frac{1}{20}$， $\frac{1}{30}$， $\frac{1}{40}$， $\frac{1}{50}$。n的候选值有6，8，10。基于这些候选值，做了15次数值实验，得到了15个Err0与15个Err1，见图1和图2。

Figure 1. Maximum absolute error

图1. 最大绝对误差

Figure 2. Mean absolute error

图2. 平均绝对误差

基于图1和图2的结果，确定出 $\Delta =\frac{1}{20}$ 和 $n=8$。

4.2. 确定数值解

确定两个参数的值后，我们得到对应的节点分布情况。图3和图4分别是节点分布的区域与边界和插值节点集。

Figure 3. Regions and borders

图3. 区域和边界

Figure 4. Interpolation node set

图4. 插值节点集

利用有限差分格式求解出方程的数值解，图5是数值解的三维图像。

为方便比较数值解与解析解的最大绝对误差和平均绝对误差，我们将两个解合并展示，见图6。其中红点为解析解值，蓝点为数值解值。

计算得到最大绝对误差Err0是0.05268，平均绝对误差Err1是0.016468。

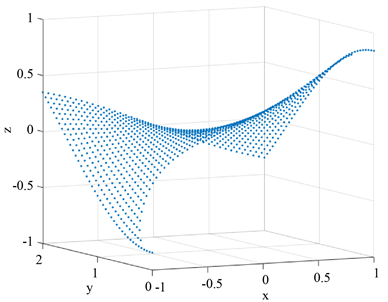
Figure 5. Numerical solution of transmission eigenvalue

图5. 透射特征值数值解

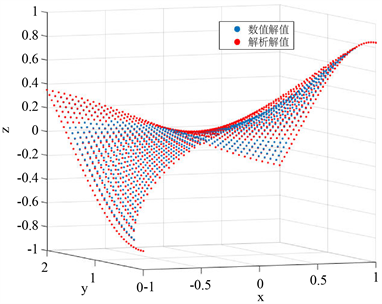
Figure 6. Numerical solution and analytical solution

图6. 数值解与解析解

5. 误差分析

5.1. 奇异性

对于本文提出的基于多元多项式插值的广义有限差分法，区域节点分布生成简单，选取插值节点集后广义有限差分公式的建立不存在奇异性问题，广义有限差分公式中权系数的计算稳定且计算量小。

5.2. 点态逼近误差

根据文献 [11] 的误差分析：

存在一个数 $\lambda \ge \text{1}$，任意两点 $p_1,p_2\in \Omega$ 可通过长度为 $\left|\Gamma \right|\le \Vert p_1-p_2\Vert$ 的可校正曲线Γ连接。

$\Omega \subset R^2$ 是满足此假设的紧致域，T是通过上述算法生成的一个节点集，给定 $n\in N,p\in \Omega$， ${\chi }_n\left(p\right)={\left\{q_{\alpha }\right\}}_{\alpha \in I_n^2}$ 是最终生成的插值节点集， ${\left\{l_{\alpha }\right\}}_{\alpha \in I_n^2}$ 是 ${\chi }_n\left(p\right)$ 生成的拉格朗日基。又

$\gamma =\left({\gamma }_1,{\gamma }_2\right)\in N_0^2,\left|\gamma \right|\le n$，若 $p\in \text{Rect}\left({\chi }_n\left(p\right)\right)\cap \Omega ,f\in C^{n,1}\left(\Omega \right)$，那么

当 $C\left(\tau ,\kappa ,\gamma ,\lambda \right)=\frac{2\frac{3n+1}{2}{\lambda }^n}{\left(n-1\right)!}{\tau }^{n+1-\left|\gamma \right|}{C}_1\left(\tau ,\kappa ,\gamma \right)$ 时，

$\left|f^{\left(\gamma \right)}\left(p\right)-{\displaystyle \underset{\alpha \in I_n^2}{\sum }f\left(q_{\alpha }\right)l_{\alpha }^{\left(\gamma \right)}\left(p\right)}\right|\le C\left(\tau ,\kappa ,\gamma ,\lambda \right){\left|f\right|}_{n,1}{\Delta }^{n+1-\left|\gamma \right|},$

其中 $C_1\left(\tau ,\kappa ,\gamma \right)={\left(2\kappa \right)}^{\left|\gamma \right|}{\left({\tau }^n+1\right)}^{\left|I_n^2\right|-1}{\displaystyle \underset{\alpha =\left(i,j\right)\in I_n^2}{\sum }{\tau }^{\left|\alpha \right|-2}{T}_{i-1}^{\left({\gamma }_1\right)}(1)T_{j-1}^{\left({\gamma }_2\right)}\left(1\right)}$。

可得近似误差为 $\left|f^{\left(\gamma \right)}\left(p\right)-{\displaystyle \underset{\alpha \in I_n^2}{\sum }f\left(q_{\alpha }\right)D^{\gamma }{l}_{\alpha }\left(p\right)}\right|$。

6. 总结与发展

对于基于多元多项式插值的广义有限差分法，我们发现其区域节点分布生成简单，选取插值节点集后广义有限差分公式的建立不存在奇异性问题，广义有限差分公式中权系数的计算稳定且计算量小，可以很好地进行Helmholtz方程Neumann问题的数值求解。

此方法还有一些需要进一步研究的地方。无网格方法的节点分布直接影响数值解的误差精度。我们希望可以根据区域自身的特点构造出具有自适应特点的平行直线型节点分布。