奇数阶始元臻美和幻方的构造方法

The Method of Constructing Odd-Order Shi Yuan Perfect Sum Magic Square

摘要: 目的：研究奇数阶始元臻美和幻方的构造方法。方法：通过构造特殊函数及固定向量与矩阵表示相结合的思路进行研究。结果与结论：给出了奇数阶始元臻美和幻方的构造方法并提出关于偶数阶臻美和幻方不存在的猜想。

Abstract: Object: To study the construction methods of odd-order Shi Yuan Perfect sum magic square. Methods: The research is carried out by constructing special function and combining fixed vector and matrix representation. Result and Conclusion: The construction methods of odd-order Shi Yuan Perfect sum magic square are given and conjecture about the existence of even-order perfect sum magic square is put forward.

1. 引言

幻方 [1] [2] 又称“河图”、“洛书”或“纵横图”，是使得m行m列矩阵每行每列以及对角线上的数字和都相等的方法。幻方作为一类特殊的整数矩阵，不仅可应用于大量的美术设计和西方建筑中，还可应用于封面包装，其重要性不言而喻，自然而然得到众多学者的青睐。而臻美和幻方作为一类特殊的整数矩阵及和幻方，其构造问题也就有必要进行深入研究。

吴硕辛老师在中国文化出版社出版的《 $mi\left(q\right)$ 语言的理论与应用》 [3] 专著中提出了臻美和幻方，并说

$\left(\begin{array}{ccccc}\text{0}& \text{13}& \text{21}& \text{9}& \text{17}\\ \text{6}& \text{19}& \text{2}& \text{10}& \text{23}\\ \text{12}& \text{20}& \text{8}& \text{16}& \text{4}\\ \text{18}& \text{1}& \text{14}& \text{22}& \text{5}\\ \text{24}& \text{7}& \text{15}& \text{3}& \text{11}\end{array}\right)$

既是臻美和幻方又是完美和幻方，而

$\left(\begin{array}{cccc}\text{0}& \text{7}& \text{9}& \text{14}\\ \text{13}& \text{10}& \text{4}& \text{3}\\ \text{6}& \text{1}& \text{15}& \text{8}\\ \text{11}& \text{12}& \text{2}& \text{5}\end{array}\right)$

是完美和幻方但不是臻美和幻方。

虽然他对臻美和幻方按其理论给出了定义，但由于其理论较为复杂且繁琐，对于大多数读者来说难以读懂，故需要对该理论进行解释补充。在通过对他提出的定义进行研究后，本文结合现今和幻方的规范定义形式，给出了臻美和幻方的相关定义、性质及奇数阶始元臻美和幻方的构造方法 [4] [5] [6]。

注：为了叙述方便，现对文中的符号进行说明。

1) 下文中规定 $m\left(\mathrm{mod}m\right)=m$。

2) 本文中 $E_{ij}\left(m,m\right)$ 表示第i行第j列的元素是1而其余元素都是零的m阶矩阵。

3) $\left(i+k\right)\left(\mathrm{mod}m\right)$ 表示 $i+k$ 对m做除法所得的余数， $\left(k-i+1\right)\left(modm\right)$ 表示 $k-i+1$ 对m做除法所得的余数。

2. 预备知识

为给出臻美和幻方的定义及其构造定理，我们需要以下定义。

定义1 [7] 若矩阵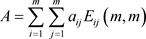， $S_{\text{1}}\in R$，(其中 $a_{ij}\in F$ $\left(i,j=1,2,\cdots ,m\right)$)满足：

①；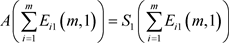

②；

③；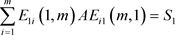

④；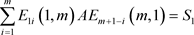

则称矩阵A为数域F上的m阶和幻方，并称S₁为m阶和幻方A的幻和。

定义2 [8] 若矩阵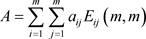， $S_{\text{2}}\in R$，(其中 $a_{ij}\in F$ $\left(i,j=1,2,\cdots ,m\right)$)满足：

①；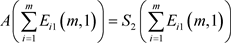

②；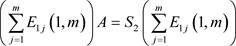

③；

④；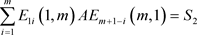

⑤ 对于 $\forall k\left(k=0,1,2,\cdots ,m-1\right)$，有 ${\displaystyle \underset{i=1}{\overset{m}{\sum }}{E}_{1i}\left(1,m\right)A{E}_{\left(k-i+1\right)\left(modm\right),1}\left(m,1\right)}=S_2$ ；

⑥ 对于 $\forall k\left(k=0,1,2,\cdots ,m-1\right)$，有 ${\displaystyle \underset{i=1}{\overset{m}{\sum }}{E}_{1i}\left(1,m\right)A}{E}_{\left(i+k\right)\left(modm\right),1}\left(m,1\right)=S_2$ ；

则称矩阵A为m阶完美和幻方，并称S₂为m阶完美和幻方A的幻和。

定义3 [9] 设矩阵 $A={\left(a_{ij}\right)}_{m\times m}\in S^{m\times m}$ ( $S=\left\{1,2,\cdots ,m\right\}$)， $\forall i,j,k\in \left\{1,2,\cdots ,m\right\}$，当 $i\ne j$ 有 $a_{ik}\ne a_{jk},a_{ki}\ne a_{kj}$，则称矩阵A为m阶拉丁方。

定义4 [10] 设矩阵 $A={\left(a_{ij}\right)}_{m\times m}\in S^{m\times m}$ ( $S=\left\{1,2,\cdots ,m\right\}$)，满足：

① 对 $\forall i,j,k\in \left\{1,2,\cdots ,m\right\}$，当 $j\ne k$ 有 $a_{ij}\ne a_{ik}$ 恒成立；

② 对 $\forall i,j,k\in \left\{1,2,\cdots ,m\right\}$，当 $j\ne k$ 有 $a_{ik}\ne a_{jk}$ 恒成立；

③ 对 $\forall i,j,k\in \left\{1,2,\cdots ,m\right\}$，当 $j\ne k$ 有 $a_{ii}\ne a_{jj}$ 恒成立；

④ 对 $\forall i,j,k\in \left\{1,2,\cdots ,m\right\}$，当 $j\ne k$ 有 $a_{m+1-i}\ne a_{m+1-j}$ 恒成立；

则称矩阵A是m阶拉丁幻方。

定义5 [8] 设矩阵 $A={\left(a_{ij}\right)}_{m\times m}\in S^{m\times m}$ ( $S=\left\{1,2,\cdots ,m\right\}$)，满足：

① 矩阵A的每一行，每一列都是 $1,2,\cdots ,m$ 的一个全排列；

② $\left\{a_{i,\left(i+k\right)\left(\mathrm{mod}m\right)}\right\}\left(k=0,1,2,\cdots ,m-1\right)$ 都是 $1,2,\cdots ,m$ 的一个全排列；

③ $\left\{a_{i,\left(k-i+1\right)\left(\mathrm{mod}m\right)}\right\}\left(k=0,1,2,\cdots ,m-1\right)$ 都是 $1,2,\cdots ,m$ 的一个全排列；

则称矩阵A是m阶完美拉丁幻方。

3. 主要结果

3.1. 定义

首先给出奇数阶始元完美和幻方的定义。

定义6 若奇数阶矩阵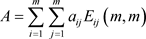， $S_3\in R$ (其中 $a_{ij}\in \left\{1,2,\cdots ,m^2\right\}$ $\left(i,j=1,2,\cdots ,m\right)$)，满足：

①；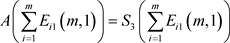

②；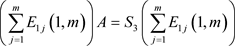

③；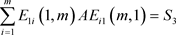

④；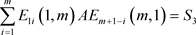

⑤ 对于 $\forall k\left(k=0,1,2,\cdots ,m-1\right)$，有 ${\displaystyle \underset{i=1}{\overset{m}{\sum }}{E}_{1i}\left(1,m\right)A}{E}_{\left(k-i+1\right)\left(modm\right),1}\left(m,1\right)=S_3$ ；

⑥ 对于 $\forall k\left(k=0,1,2,\cdots ,m-1\right)$，有 ${\displaystyle \underset{i=1}{\overset{m}{\sum }}{E}_{1i}\left(1,m\right)A}{E}_{\left(i+k\right)\left(modm\right),1}\left(m,1\right)=S_3$ ；

当 $i\ne k$ 或 $j\ne l$ 时有 $a_{ij}\ne a_{kl}$ $\left(i,j,k,l=1,2,\cdots ,m\right)$，则称矩阵A为m阶始元完美和幻方，并称S₃为m阶始元完美和幻方A的幻和。

由于奇数阶始元完美和幻方是特殊的奇数阶连元完美和幻方，所以就有如下定义。

定义7 若奇数阶矩阵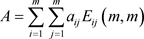， $S_4\in R$ (其中 $a_{ij}\in \left\{a+1,a+2,\cdots ,a+m^2\right\}$ $\left(a\in Z\right)$

$\left(i,j=1,2,\cdots ,m\right)$)，满足以下条件：

①；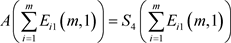

②；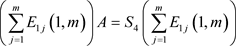

③；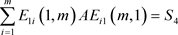

④；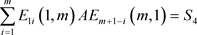

⑤ 对于 $\forall k\left(k=0,1,2,\cdots ,m-1\right)$，有 ${\displaystyle \underset{i=1}{\overset{m}{\sum }}{E}_{1i}\left(1,m\right)A}{E}_{\left(k-i+1\right)\left(modm\right),1}\left(m,1\right)=S_4$ ；

⑥ 对于 $\forall k\left(k=0,1,2,\cdots ,m-1\right)$，有 ${\displaystyle \underset{i=1}{\overset{m}{\sum }}{E}_{1i}\left(1,m\right)A}{E}_{\left(i+k\right)\left(modm\right),1}\left(m,1\right)=S_4$ ；

当 $i\ne k$ 或 $j\ne l$ 时有 $a_{ij}\ne a_{kl}$， $\left(i,j,k,l=1,2,\cdots ,m\right)$，则称矩阵A为m阶连元完美和幻方，并称S₄为m阶连元完美和幻方A的幻和。

又由于奇数阶连元完美和幻方是特殊的奇数阶异元完美和幻方，所以也就有如下定义。

定义8 若奇数阶矩阵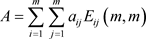， $S_5\in R$，(其中 $a_{ij}\in \left\{a_1,a_2,\cdots ,a_{n^2}\right\}$ $\left(i,j=1,2,\cdots ,m\right)$)且 $\forall i,j\in \left\{1,2,\cdots ,m^2\right\}$ 当 $i\ne j$ 时 $a_i\ne a_j$，满足：

①；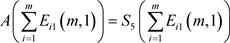

②；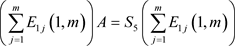

③；

④；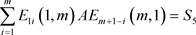

⑤ 对于 $\forall k\left(k=0,1,2,\cdots ,m-1\right)$，有 ${\displaystyle \underset{i=1}{\overset{m}{\sum }}{E}_{1i}\left(1,m\right)A}{E}_{\left(k-i+1\right)\left(modm\right),1}\left(m,1\right)=S_5$ ；

⑥ 对于 $\forall k\left(k=0,1,2,\cdots ,m-1\right)$，有 ${\displaystyle \underset{i=1}{\overset{m}{\sum }}{E}_{1i}\left(1,m\right)A}{E}_{\left(i+k\right)\left(modm\right),1}\left(m,1\right)=S_5$ ；

当 $i\ne k$ 或 $j\ne l$ 时有 $a_{ij}\ne a_{kl}$， $\left(i,j,k,l=1,2,\cdots ,m\right)$，则称矩阵A为m阶异元完美和幻方，并称S₅为m阶异元完美和幻方A的幻和。

接下来，我们给出奇数阶始元臻美和幻方的定义。

定义9 若奇数阶矩阵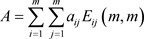， $S_6\in R$，(其中 $a_{ij}\in \left\{1,2,\cdots ,m^2\right\}$ $\left(i,j=1,2,\cdots ,m\right)$)，满足：

① $a_{11},a_{12},\cdots ,a_{1m},a_{21},\cdots ,a_{2m},\cdots ,a_{m1},\cdots ,a_{mm}$ 是 $1,2,\cdots ,m^2$ 的一个全排列；

②；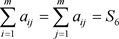

③ $\underset{i=1}{\overset{m}{{\displaystyle \sum }}}{a}_{i,\left(i+k\right)\left(\mathrm{mod}m\right)}=\underset{i=1}{\overset{m}{{\displaystyle \sum }}}{a}_{i,\left(k-i+1\right)\left(\mathrm{mod}m\right)}=S_6$，其中 $\left(k=0,1,2,\cdots ,m-1\right)$ ；

④ $A=B+mC$ (B、C都是m阶完美拉丁幻方)；

则称A为m阶始元臻美和幻方，并称S₆为m阶始元臻美和幻方A的幻和。

定义10 若奇数阶矩阵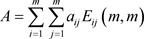， $S_7\in R$ (其中 $a_{ij}\in \left\{a+1,a+2,\cdots ,a+m^2\right\}$ $\left(a\in Z\right)$ $\left(i,j=1,2,\cdots ,m\right)$)，满足：

① $a_{11},a_{12},\cdots ,a_{1m},a_{21},\cdots ,a_{2m},\cdots ,a_{m1},\cdots ,a_{mm}$ 是 $a+1,a+2,\cdots ,a+m^2$ 的一个全排列；

②；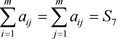

③ $\underset{i=1}{\overset{m}{{\displaystyle \sum }}}{a}_{i,\left(i+k\right)\left(\mathrm{mod}m\right)}=\underset{i=1}{\overset{m}{{\displaystyle \sum }}}{a}_{i,\left(k-i+1\right)\left(\mathrm{mod}m\right)}=S_7$，其中 $\left(k=0,1,2,\cdots ,m-1\right)$ ；

④ $A=B+mC$ (B、C都是m阶完美拉丁幻方)；

则称A为m阶连元臻美和幻方，并称S₇为m阶连元臻美和幻方A的幻和。

定义11 若奇数阶矩阵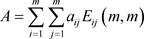， $S_8\in R$ (其中 $a_{ij}\in \left\{a_1,a_2,\cdots ,a_{n^2}\right\}$ $\left(i,j=1,2,\cdots ,m\right)$)且 $\forall i,j\in \left\{1,2,\cdots ,m^2\right\}$ 当 $i\ne j$ 时 $a_i\ne a_j$，满足：

① $a_{11},a_{12},\cdots ,a_{1m},a_{21},\cdots ,a_{2m},\cdots ,a_{m1},\cdots ,a_{mm}$ 是 $a_1,a_2,\cdots ,a_{n^2}$ 的一个全排列；

②；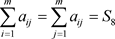

③ $\underset{i=1}{\overset{m}{{\displaystyle \sum }}}{a}_{i,\left(i+k\right)\left(\mathrm{mod}m\right)}=\underset{i=1}{\overset{m}{{\displaystyle \sum }}}{a}_{i,\left(k-i+1\right)\left(\mathrm{mod}m\right)}=S_8$，其中 $\left(k=0,1,2,\cdots ,m-1\right)$ ；

④ $A=B+mC$ (B，C都是m阶完美拉丁幻方)；

则称A为m阶异元臻美和幻方，并称S₈为m阶异元臻美和幻方A的幻和。

为了证明奇数阶臻美和幻方的构造定理，下面我们给出具有和幻性矩阵的定义。

定义12 设奇数阶矩阵 $A={\left(a_{ij}\right)}_{m\times m}$，如果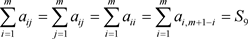，则称A是具有和幻性的m阶矩阵，S₉为m阶矩阵A的幻和。

3.2. 性质

根据臻美和幻方的定义可知，有以下结论成立。

性质1. 设奇数阶矩阵 $A={\left(a_{ij}\right)}_{n\times n}$ 是异元臻美和幻方，并且规定 $n\left(\mathrm{mod}n\right)=n$，则 $\forall k=0,1,2,\cdots ,n-1$ 有 ${\left(a_{\left(i+k\right)\left(\mathrm{mod}n\right),j}\right)}_{n\times n}$ 及 ${\left(a_{i,\left(j+k\right)\left(\mathrm{mod}n\right)}\right)}_{n\times n}$ 也是异元臻美和幻方。

由于连元臻美和幻方是特殊的异元臻美和幻方，始元臻美和幻方是特殊的连元臻美和幻方，所以有以下推论成立。

推论1. 设奇数阶矩阵 $A={\left(a_{ij}\right)}_{n\times n}$ 是连元臻美和幻方，并且规定 $n\left(\mathrm{mod}n\right)=n$，则 $\forall k=0,1,2,\cdots ,n-1$ 有 ${\left(a_{\left(i+k\right)\left(\mathrm{mod}n\right),j}\right)}_{n\times n}$ 及 ${\left(a_{i,\left(j+k\right)\left(\mathrm{mod}n\right)}\right)}_{n\times n}$ 也是连元臻美和幻方。

推论2. 设奇数阶矩阵 $A={\left(a_{ij}\right)}_{n\times n}$ 是始元臻美和幻方，并且规定 $n\left(\mathrm{mod}n\right)=n$，则 $\forall k=0,1,2,\cdots ,n-1$ 有 ${\left(a_{\left(i+k\right)\left(\mathrm{mod}n\right),j}\right)}_{n\times n}$ 及 ${\left(a_{i,\left(j+k\right)\left(\mathrm{mod}n\right)}\right)}_{n\times n}$ 也是始元臻美和幻方。

性质2. 如果奇数阶矩阵 $A={\left(a_{ij}\right)}_{n\times n}$ 是异元臻美和幻方，且幻和为 $\Delta$ ( $\Delta$ is u-digit number，即 $\Delta$ 是一个u位数)，规定 $n\left(\mathrm{mod}n\right)=n$，将 $a_{ij}$ 变为 $c_{ij}{a}_{ij}=d_{ij}$ (其中 $a_{ij}$ is $k_{ij}$ -digit number (即 $a_{ij}$ 是一个 $k_{ij}$ 位数)， $c_{ij}$ is $u-k_{ij}$ -digit number (即 $c_{ij}$ 是一个 $u-k_{ij}$ 位数) $\left(i,j=0,1,2,\cdots ,n\right)$)，则有

$\begin{array}{c}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{d}_{i1}{d}_{i2}\cdots d_{in}}={\displaystyle \underset{j=1}{\overset{n}{\sum }}{d}_{1j}{d}_{2j}\cdots d_{nj}}\\ ={\displaystyle \underset{j=1}{\overset{n}{\sum }}{d}_{1,\left(1+j\right)\left(modn\right)}{d}_{2,\left(2+j\right)\left(modn\right)}\cdots d_{n,\left(n+j\right)\left(modn\right)}}\\ ={\displaystyle \underset{j=1}{\overset{n}{\sum }}{d}_{n,\left(1+j\right)\left(modn\right)}{d}_{n-1,\left(2+j\right)\left(modn\right)}\cdots d_{1,\left(n+j\right)\left(modn\right)}}\end{array}$

3.3. 奇数阶臻美和幻方的构造方法

定理1 设 $\alpha ={\left(0,1,2,\cdots ,2n\right)}^{\text{T}}$， $\beta =\alpha +{\left(1,1,\cdots ,1\right)}^{\text{T}}$，对 $\forall x={\left(x_1,x_2,\cdots ,x_{2n+\text{1}}\right)}^{\text{T}}$ 规定：

$f\left(x\right)=\left(x_{n+1},x_{n\text{+}2},\cdots ,x_{2n+\text{1}},x_1,\cdots ,x_n\right)$

$g\left(x\right)=\left(x_{n+2},x_{n\text{+3}},\cdots ,x_{2n+\text{1}},x_1,\cdots ,x_{n+1}\right)$ ;

利用 $f\left(x\right)$ 及 $g\left(x\right)$ 构造 $2n+1$ 阶矩阵B及C如下：

$B=\left(\beta ,f\left(\beta \right),f^2\left(\beta \right),f^3\left(\beta \right),\cdots ,f^{2n}(\; \beta \; )\right)$

$C=\left(\alpha ,g\left(\alpha \right),g^2\left(\alpha \right),g^3\left(\alpha \right),\cdots ,g^{2n}\left(\alpha \right)\right)$ ;

如果 $2n+1$ 阶矩阵B，C为 $2n+1$ 阶完美拉丁幻方，则称矩阵 $A=B+\left(2n+1\right)C$ 是 $2n+1$ 阶始元臻美和幻方。

证明：要证明矩阵A是 $2n+1$ 阶始元臻美和幻方，就需要完成以下四步：

① A是具有和幻性的矩阵；

② A中的元素两两互不相等；

③ A中的元素取自集合 $\left\{1,2,\cdots ,{\left(2n+1\right)}^2\right\}$ ；

④ B，C是完美拉丁幻方。

第一步：

由于B，C是完美拉丁幻方，则B，C是具有和幻性的矩阵。又由于 $A=B+\left(2n+1\right)C$ 且具有和幻性矩阵的线性组合仍然是具有和幻性的矩阵。则矩阵A就是具有和幻性的矩阵。

第二步：

由于B是关于 $1,2,\cdots ,2n+1$ 的拉丁幻方，而C是关于 $0,1,\cdots ,2n$ 的拉丁幻方，且 $A=B+\left(2n+1\right)C$，则B与C正交。则 $a_{ij}=b_{ij}+\left(2n+1\right)c_{ij}$，对 $\forall i,j\in \left\{1,2,\cdots ,2n+1\right\}$ 两两互不相等，则 $a_{ij}$ $\left(i,j=1,2,\cdots ,2n+1\right)$两两互不相等，也即A是 $2n+1$ 阶异元臻美和幻方。

第三步：

由于 $1\le b_{ij}\le 2n+1$， $1\le c_{ij}\le 2n$，则 $1\le b_{ij}+\left(2n+1\right)c_{ij}\le {\left(2n+1\right)}^2$，则 $a_{ij}\in \left\{1,2,\cdots ,{\left(2n+1\right)}^2\right\}$ $\left(i,j=1,2,\cdots ,2n+1\right)$，也即A是 $2n+1$ 阶始元臻美和幻方。

第四步：

由已知可知B，C是完美拉丁幻方。

综合以上可知，矩阵A即为 $2n+1$ 阶始元臻美和幻方。

注：

奇数阶始元臻美和幻方的构造方法也是奇数阶始元完美和幻方的构造方法，同样也是奇数阶始元和幻方的构造方法。但奇数阶始元和幻方的构造方法不一定能构造出奇数阶始元完美和幻方，同时奇数阶始元完美和幻方的构造方法不一定能构造出奇数阶始元臻美和幻方。

(由于奇数阶始元臻美和幻方是特殊的奇数阶始元完美和幻方，也是特殊的奇数阶始元和幻方，故这两类和幻方是存在的且对应的奇数阶定义是有意义的。)

推论3 设 $\alpha ={\left(0+a,1+a,2+a,\cdots ,2n+a\right)}^{\text{T}}$ $\left(a\in Z\right)$， $\beta =\alpha +{\left(1,1,\cdots ,1\right)}^{\text{T}}$，对 $\forall x={\left(x_1,x_2,\cdots ,x_{2n+\text{1}}\right)}^{\text{T}}$ 规定

$f\left(x\right)=\left(x_{n+1},x_{n\text{+}2},\cdots ,x_{2n+\text{1}},x_1,\cdots ,x_n\right)$

$g\left(x\right)=\left(x_{n+2},x_{n\text{+3}},\cdots ,x_{2n+\text{1}},x_1,\cdots ,x_{n+1}\right)$ ;

利用 $f\left(x\right)$ 及 $g\left(x\right)$ 构造 $2n+1$ 阶矩阵B及C如下：

$B=\left(\beta ,f\left(\beta \right),f^2\left(\beta \right),f^3\left(\beta \right),\cdots ,f^{2n}(\; \beta \; )\right)$

$C=\left(\alpha ,g\left(\alpha \right),g^2\left(\alpha \right),g^3\left(\alpha \right),\cdots ,g^{2n}\left(\alpha \right)\right)$ ;

如果 $2n+1$ 阶矩阵B、C为 $2n+1$ 阶完美拉丁幻方，则称矩阵 $A=B+\left(2n+1\right)C$ 是 $2n+1$ 阶连元臻美和幻方。

由于定理及推论中涉及到的这 $2n+1$ 个元素都是两两互不相等的，所以始元臻美和幻方的构造方法也是异元臻美和幻方的构造方法。

接下来通过例子验证定义9及定理1的正确性。

例1. 给出一个11阶始元臻美和幻方。

解：由奇数阶臻美和幻方的构造定理1知，n阶完美拉丁幻方B，C分别为：

$B={\left(\begin{array}{ccccccccccc}1& 6& 11& 5& 10& 4& 9& 3& 8& 2& 7\\ 2& 7& 1& 6& 11& 5& 10& 4& 9& 3& 8\\ 3& 8& 2& 7& 1& 6& 11& 5& 10& 4& 9\\ 4& 9& 3& 8& 2& 7& 1& 6& 11& 5& 10\\ 5& 10& 4& 9& 3& 8& 2& 7& 1& 6& 11\\ 6& 11& 5& 10& 4& 9& 3& 8& 2& 7& 1\\ 7& 1& 6& 11& 5& 10& 4& 9& 3& 8& 2\\ 8& 2& 7& 1& 6& 11& 5& 10& 4& 9& 3\\ 9& 3& 8& 2& 7& 1& 6& 11& 5& 10& 4\\ 10& 4& 9& 3& 8& 2& 7& 1& 6& 11& 5\\ 11& 5& 10& 4& 9& 3& 8& 2& 7& 1& 6\end{array}\right)}_{11\times 11}$

$C={\left(\begin{array}{ccccccccccc}0& 6& 1& 7& 2& 8& 3& 9& 4& 10& 5\\ 1& 7& 2& 8& 3& 9& 4& 10& 5& 0& 6\\ 2& 8& 3& 9& 4& 10& 5& 0& 6& 1& 7\\ 3& 9& 4& 10& 5& 0& 6& 1& 7& 2& 8\\ 4& 10& 5& 0& 6& 1& 7& 2& 8& 3& 9\\ 5& 0& 6& 1& 7& 2& 8& 3& 9& 4& 10\\ 6& 1& 7& 2& 8& 3& 9& 4& 10& 5& 0\\ 7& 2& 8& 3& 9& 4& 10& 5& 0& 6& 1\\ 8& 3& 9& 4& 10& 5& 0& 6& 1& 7& 2\\ 9& 4& 10& 5& 0& 6& 1& 7& 2& 8& 3\\ 10& 5& 0& 6& 1& 7& 2& 8& 3& 9& 4\end{array}\right)}_{11\times 11}$

则矩阵

$A={\left(\begin{array}{ccccccccccc}1& \text{72}& \text{22}& \text{82}& \text{32}& \text{92}& \text{42}& \text{102}& \text{52}& \text{112}& \text{62}\\ 13& \text{84}& 23& \text{94}& \text{44}& \text{104}& \text{54}& \text{114}& \text{64}& 3& \text{74}\\ 25& \text{96}& \text{35}& \text{106}& 45& \text{116}& \text{66}& 5& \text{76}& \text{15}& \text{86}\\ 37& \text{108}& \text{47}& \text{118}& \text{57}& 7& 67& \text{17}& \text{88}& \text{27}& \text{98}\\ 49& \text{120}& \text{59}& 9& \text{69}& \text{19}& \text{79}& \text{29}& 89& \text{39}& \text{110}\\ \text{61}& \text{11}& \text{71}& \text{21}& \text{81}& \text{31}& \text{91}& \text{41}& \text{101}& \text{51}& 111\\ \text{73}& \text{12}& \text{83}& \text{33}& \text{93}& \text{43}& \text{103}& \text{53}& \text{113}& \text{63}& 2\\ \text{85}& \text{24}& \text{95}& 34& \text{105}& \text{55}& \text{115}& \text{65}& 4& \text{75}& \text{14}\\ \text{97}& \text{36}& \text{107}& \text{46}& \text{117}& 56& 6& \text{77}& \text{16}& \text{87}& \text{26}\\ \text{109}& \text{48}& \text{119}& \text{58}& 8& \text{68}& \text{18}& 78& \text{28}& \text{99}& \text{38}\\ \text{121}& \text{60}& 10& 70& 20& 80& 30& 90& 40& 100& 50\end{array}\right)}_{11\times 11}$

对于矩阵A中的任意元素 $a_{ij}$，都有 $a_{ij}\in \left\{1,2,\cdots ,{\text{11}}^2\right\}$ $\left(i,j=1,2,\cdots ,\text{11}\right)$)，满足：

① $a_{11},a_{12},\cdots ,a_{1，11},a_{21},\cdots ,a_{2，11},\cdots ,a_{11，1},\cdots ,a_{11，11}$ 是 $1,2,\cdots ,{\text{11}}^2$ 的一个全排列；

②；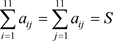

③ $\underset{i=1}{\overset{\text{11}}{{\displaystyle \sum }}}{a}_{i,\left(i+k\right)\left(\mathrm{mod}\text{11}\right)}=\underset{i=1}{\overset{\text{11}}{{\displaystyle \sum }}}{a}_{i,\left(k-i+1\right)\left(\mathrm{mod}\text{11}\right)}=S$，其中 $\left(k=0,1,2,\cdots ,\text{11}-1\right)$ ；

④ $A=B+\text{11}C$ (B、C都是m阶完美拉丁幻方)；

因此，矩阵 $A={\left(a_{ij}\right)}_{11\times 11}$ 满足定义9的条件。

所以，矩阵A为11阶始元臻美和幻方。

4. 偶数阶臻美和幻方的存在性

由奇数阶臻美和幻方的构造定理知，奇数阶臻美和幻方是存在的，但我们通过计算机程序求解得到 $n\left(n\ge 50\right)$ 阶的所有和幻方，对其进行 $A=B+nC$ 形式的分解，分解后发现B和C只有一个是拉丁幻方，另一个不是拉丁幻方。又由任意的一个始元和幻方都可以分解为一个行拉丁方和一个列拉丁方的形式 [3]，所以我们猜想：偶数阶臻美和幻方不存在。

关于此猜想的证明，目前来说，我们没有找到一个合适的证明方法，只有通过列举法把一些情况进行否定，具体证明方式有待于日后再做进一步的研究。

5. 小结

本文利用了构造特殊函数及固定向量与矩阵表示相结合的思路，研究了奇数阶始元臻美和幻方的构造方法，并通过具体例子验证了定义9及定理1的正确性，最后提出关于偶数阶臻美和幻方不存在的猜想。

NOTES

^*惠晶(1998-)，女，陕西榆林人，延安大学本科生。

^#通讯作者。刘兴祥(1964-)，男，陕西合阳人，副教授，硕士生导师，研究方向：矩阵理论。