均布载荷作用下圆底扁薄球壳非线性屈曲问题的新解析解

A New Analytical Solution for the Nonlinear Buckling of Shallow Thin Spherical Shells with Circular Bottom under Uniformly Distributed Loads

摘要: 本文中考虑了在均布载荷作用下，周边固定的圆底扁薄球壳的非线性屈曲问题。我们利用Adomian分解法得到了该非线性屈曲问题的新解析近似解。基于新解析解讨论了具有各种k值对应的中心挠度与载荷的特征曲线。得到的结果与修正迭代法得到的结果非常吻合，便说明得到的新解析解的有效性和准确性。

Abstract: Nonlinear buckling problem of shallow thin spherical shell with circular bottom and fixed periphery under uniform load is considered in this paper. We use the Adomian decomposition method to obtain a new analytical approximate solution to the nonlinear buckling problem. Based on the new analytical solution, the characteristic curves of center deflection and load corresponding to various k values are discussed. The results obtained in this paper are very consistent with the results obtained by the modified iterative method, which shows the validity and accuracy of the new analytical solution obtained.

1. 引言

扁球壳的非线性屈曲对其在工程中的应用影响很大。但其屈曲程度很难确定。本文中我们考虑在均布载荷作用下圆底扁薄球壳的非线性屈曲问题，该问题的控制方程为

$D\frac{\text{d}}{\text{d}r}\frac{1}{r}\frac{\text{d}}{\text{d}r}r\cdot \frac{\text{d}w}{\text{d}r}-N_r\left(\frac{r}{R}+\frac{\text{d}w}{\text{d}r}\right)-\frac{qr}{2}=0$ (1)

$\frac{r}{Eh}\frac{\text{d}}{\text{d}r}\frac{1}{r}\frac{\text{d}}{\text{d}r}\left(r^2\cdot N_r\right)+\frac{\text{d}w}{\text{d}r}\left(\frac{r}{R}+\frac{1}{2}\frac{\text{d}w}{\text{d}r}\right)=0$ (2)

边缘固定夹紧时，边界条件为

$r=a$ 处， $\frac{\text{d}w}{\text{d}r}=0$， $w=0$， $r\cdot \frac{\text{d}{N}_r}{\text{d}r}+\left(1-\mu \right)\cdot N_r=0$ (3)

$r=0$ 处， $\frac{\text{d}w}{\text{d}r}=0$， $\left|N_r\right|<+\infty$， $\left|w\right|<+\infty$ (4)

其中R为球壳中面的半径，h为壳体的厚度， $N_r$ 为径向薄膜内力，a为扁球壳圆底的半径， $M_r$ 为径向弯矩， $\mu$ 为材料的泊松比，w为中曲面的挠度，E为弹性模量，q为横向载荷强度， $D=\frac{Eh}{12\left(1-\mu \right)}$。

为了得到这类问题的屈曲程度，研究人员应用了很多方法，如S. Way等人 [1] [2] 利用幂级数法求解了圆底扁球壳非线性稳定问题；赵伟东 [3] 等人用打靶法分析了扁球壳在热–机械荷载作用下的稳定性；刘人怀 [4] 等人采用改进的迭代法讨论了双层网状扁球壳非线性弯曲问题；顾淑贤 [5] 用三次B样条函数和迭代法得出均布荷载作用下周边固定圆底扁球壳轴对称弯曲问题的解；侯朝胜等人 [6] 用配点法计算了夹层圆板和夹层扁球壳的非线性弯曲问题；叶开沅 [7] 通过修正迭代法得到周边固定的圆底扁薄球壳临界载荷的二次近似解析解。本文中我们将运用以上方法不同的方法——Adomian分解法研究该扁球壳的非线性屈曲问题的新近似解。

Adomian分解法对于求解非线性微分方程有其独特的优点，相比传统摄动方法，Adomian分解法不再需要小参数，且对非线性微分方程中的非线性部分用Adomian多项式代替，从而简化原非线性方程。所以Adomian分解法被广泛应用到许多非线性微分方程边值问题中，如段俊生等人 [8] [9] 把Adomian分解方法应用于分数阶微分方程组以及高阶非线性微分方程的边值问题；Wazwaz [10] [11] 把Adomian分解方法应用于变系数的高维初始边界值问题、具有初始值和边界条件的Lane-Emden方程；温颖等人 [12] 结合分段技术与Adomian分解法求解了三角形区域二阶偏微分方程的边值问题；云银山等人 [13] 基于Adomian分解法，提出一种新算法解决矩形区域非线性微分方程边值问题；李丹丹等人 [14] 基于Adomian分解法，求解三角形地下水域上补给效应模型的Dirichlet边值问题；刘慧等人 [15] 基于Adomian分解法考虑了边界简单铰链支撑的圆薄板大挠度问题。

本文中，借助Adomian分解法的优点，将研究扁球壳非线性屈曲问题的新近似解。具体内容如下：第二节利用Adomian分解法计算了该圆底扁球壳问题的新的解析解；最后一节我们确定了无量纲载荷与中心挠度的特征曲线，并证明该方法的有效性与准确性。

2. Adomian解析近似解

首先通过以下无量纲变换：

$\rho =\frac{r^2}{a^2}$, $S=\frac{N_r{a}^2}{E{h}^3}$, $P=\frac{q{a}^4}{E{h}^4}\left(1-{\mu }^2\right)$, $W=\frac{w}{h}$, $k=\frac{a^2}{Rh}$, $\phi =\frac{k}{2}+\frac{\text{d}W}{\text{d}\rho }$, ${\lambda }^2=\sqrt{12\left(1-{\mu }^2\right)}\cdot k$

将方程(1)和(2)化为无量纲方程

$\frac{{\text{d}}^2}{\text{d}{\rho }^2}\left(\rho \cdot \phi \right)-3\left(1-{\mu }^2\right)\cdot S\cdot \phi -\frac{3}{4}P=0$ (5)

$\frac{{\text{d}}^2}{\text{d}{\rho }^2}\left(\rho \cdot S\right)+\frac{1}{2}\left[{\phi }^2-{\left(\frac{k}{2}\right)}^2\right]=0$ (6)

边界条件为

$\rho =1$ : $W=0$, $\phi =\frac{k}{2}$, $2\rho \frac{\text{d}S}{\text{d}\rho }+\left(1-\mu \right)S=0$ (7)

$\rho =0$ : $\left|W\right|<+\infty$, $\left|S\right|<+\infty$ (8)

为了确定逆算子 $L^{-1}$，在方程(5)两边进行从0到 $\rho$ 的两次积分，则得

$\phi \left(\rho \right)=\phi \left(0\right)+\frac{1}{\rho }{\displaystyle {\int }_0^{\rho }{\displaystyle {\int }_0^{\rho }3\left(1-{\mu }^2\right)\cdot S\cdot \phi \text{d}\rho \text{d}\rho }}+\frac{1}{\rho }{\displaystyle {\int }_0^{\rho }{\displaystyle {\int }_0^{\rho }\frac{3}{4}P\text{d}\rho \text{d}\rho }}$ (9)

令 $\rho =1$，从(9)得到

$\phi \left(0\right)=\phi \left(1\right)-{\displaystyle {\int }_0^1{\displaystyle {\int }_1^{\rho }3\left(1-{\mu }^2\right)\text{d}\rho \text{d}\rho }}-{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{\rho }\frac{3}{4}P\text{d}\rho \text{d}\rho }}$ (10)

再将(10)代入(9)中，得到

$\phi =\phi \left(1\right)-{\displaystyle {\int }_0^1{\displaystyle {\int }_1^{\rho }3\left(1-{\mu }^2\right)\cdot S\cdot \phi +\frac{3}{4}P\text{d}\rho \text{d}\rho }}+\frac{1}{\rho }{\displaystyle {\int }_0^{\rho }{\displaystyle {\int }_1^{\rho }3\left(1-{\mu }^2\right)\cdot S\cdot \phi +\frac{3}{4}P\text{d}\rho \text{d}\rho }}$

令逆算子为

$L^{-1}[\cdot ]=\frac{1}{\rho }{\displaystyle {\int }_0^{\rho }{\displaystyle {\int }_0^{\rho }[\cdot ]\text{d}\rho \text{d}\rho }}-{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{\rho }[\cdot ]\text{d}\rho \text{d}\rho }}$

依据圆底扁薄球壳基本方程对变量进行如下分解：

$\phi ={\displaystyle {\sum }_{n=0}^{\infty }{\phi }_n}$, $S={\displaystyle {\sum }_{n=0}^{\infty }{S}_n}$, $P={\displaystyle {\sum }_{n=0}^{\infty }{P}_n}$ (11)

把非线性项展开为:

$N_1\left(S,\phi \right)=3\left(1-{\mu }^2\right)\cdot S\cdot \phi ={\displaystyle {\sum }_{n=0}^{\infty }{A}_n}$

$N_2\left(\phi \right)=\frac{{\phi }^2}{2}={\displaystyle {\sum }_{n=0}^{\infty }{B}_n}$, $\left(n\ge 0\right)$ (12)

其中

$A_0=3\left(1-{\mu }^2\right)S_0{\phi }_0$

$A_1=3\left(1-{\mu }^2\right)\left(S_0{\phi }_1+S_1{\phi }_0\right)$

$A_2=3\left(1-{\mu }^2\right)\left(S_0{\phi }_2+S_1{\phi }_1+S_2{\phi }_0\right)$

$⋮$

$B_0=\frac{{\phi }_0^2}{2}$

$B_1={\phi }_0{\phi }_1$

$B_2=\frac{{\phi }_1^2}{2}+{\phi }_0{\phi }_2$

$⋮$

根据条件 $\rho =0$ 时， $W=W_0$ ； $\rho =1$ 时， $W=\frac{1}{2}k{\rho }^2$

得

$W_0={\displaystyle {\int }_0^1\left(\frac{k}{2}-\phi \right)\text{d}\rho }$

其中 $W_0$ 是壳体的无量纲中心挠度， $W_0={\frac{w}{h}|}_{r=0}$。

令

$W_0={\displaystyle {\int }_0^1\left(\frac{k}{2}-{\phi }_0\right)\text{d}\rho }$ (13)

则有

${\displaystyle {\int }_0^1{\phi }_0\text{d}\rho }={\displaystyle {\int }_0^1{\phi }_1\text{d}\rho }=\cdots ={\displaystyle {\int }_0^1{\phi }_n\text{d}\rho }=0$ (14)

方程(13)~(14)主要用于特征方程的确定。

在方程(5)两边作用逆算子 $L^{-1}$，根据边界条件(7)，有

$\phi =\frac{k}{2}+L^{-1}\left[\frac{3}{4}P\right]+L^{-1}\left[3\left(1-{\mu }^2\right)\cdot S\cdot \phi \right]$ (15)

将(11)~(12)代入(15)，得到

${\displaystyle {\sum }_{n=0}^{\infty }{\phi }_n}=\frac{k}{2}+L^{-1}\left[\frac{3}{4}{\displaystyle {\sum }_{n=0}^{\infty }{P}_n}\right]+L^{-1}\left[{\displaystyle {\sum }_{n=0}^{\infty }{A}_n}\right]$ (16)

再将(11)~(12)代入方程(6)，

$\frac{{\text{d}}^2}{\text{d}{\rho }^2}\left[\rho \cdot {\displaystyle {\sum }_{n=0}^{\infty }{S}_n}\right]+{\displaystyle {\sum }_{n=0}^{\infty }{B}_n}-\frac{k^2}{8}=0$ (17)

边界条件(7)~(8)可写为

$\rho =1$ : ${\displaystyle {\sum }_{n=0}^{\infty }{\phi }_n}=\frac{k}{2}$, $2{\frac{\text{d}}{\text{d}\rho }\left[{\displaystyle {\sum }_{n=0}^{\infty }{S}_n}\right]|}_{\rho =1}+{\frac{1-\mu }{\rho }{\displaystyle {\sum }_{n=0}^{\infty }{S}_n}|}_{\rho =1}=0$ (18)

$\rho =0$, $\left|{\displaystyle {\sum }_{n=0}^{\infty }{\phi }_n}\right|<+\infty$, $\left|{\displaystyle {\sum }_{n=0}^{\infty }{S}_n}\right|<+\infty$ (19)

根据(16)~(17)，考虑边界条件(18)~(19)，我们可构造如下一系列递推式边值问题：

$\{\begin{array}{l}{\phi }_0-\frac{k}{2}-L^{-1}\left[\frac{3}{4}{P}_0\right]=0\\ \frac{{\text{d}}^2{S}_0}{\text{d}{\rho }^2}+B_0-\frac{k^2}{8}=0\\ \left|{\phi }_0\right|<+\infty \\ \left|S_0\right|<+\infty \end{array}$ (20)

$\{\begin{array}{l}{\phi }_n-L^{-1}\left[\frac{3}{4}{P}_n\right]-L^{-1}\left[A_{n-1}\right]=0\\ \frac{{\text{d}}^2{S}_n}{\text{d}{\rho }^2}+B_n=0\\ {2\frac{{\text{d}}^2{S}_n}{\text{d}{\rho }^2}|}_{\rho =1}+{\left(1-\mu \right)\frac{S_n}{\rho }|}_{\rho =1}=0\\ \left|{\phi }_n\right|<+\infty ,\left|S_n\right|<+\infty \end{array}$ (21)

首先由(20)得

${\phi }_0=\frac{3}{8}{P}_0\rho -\frac{3}{8}{P}_0+\frac{k}{2}$ (22)

代入(13)中，

$W_0={\displaystyle {\int }_0^1\left(\frac{k}{2}-{\phi }_0\right)\text{d}\rho }=\frac{3}{16}{P}_0$

得到

$P_0=\frac{16}{3}{W}_0$ (23)

将(23)代入(22)，得到 $\phi$ 的一次近似

${\phi }_0=2W_0\rho -2W_0+\frac{k}{2}$

接着求解(20)的第二个方程得到S的一次近似

$S_0=-\frac{W_0\left(k\left(2\left(\mu -2\right)-3\rho \left(\mu -1\right)+{\rho }^2\left(\mu -1\right)\right)+W_0\left(5+6\rho \left(\mu -1\right)-4{\rho }^2\left(\mu -1\right)+\left(\mu -1\right)-3\mu \right)\right)}{6\left(-1+\mu \right)}$

再将一次近似 ${\phi }_0$ 、 $S_0$ 代入方程(21)，得到

${\phi }_1=a{W}_0^3+b{W}_0^2+c{W}_0+d$ (24)

其中

$a=\frac{\left(\mu -1\right)\left(-77+37\mu \right)+\rho \left(\mu -1\right)\left(\rho \left(110+\rho \left(50+\rho \left(2\rho -15\right)\right)\left(\mu -1\right)-90\mu \right)+30\left(3\mu -5\right)\right)}{60}$

$b=\frac{k\left(1+\mu \right)\left(-75+31\mu \right)+k\rho \left(1+\mu \right)\left(126-66\mu +\rho \left(-68+\rho \left(3\rho -20\right)\left(\mu -1\right)+52\mu \right)\right)}{48}$

$c=\frac{k^2\rho \left(12\left(\mu -2\right)+\left(\rho -6\right)\rho \left(\mu -1\right)-k^2\left(1+\mu \right)\left(7\mu -19\right)\right)}{48}$

$d=-\frac{3}{8}{P}_1+\frac{3}{8}{P}_1\rho$

由(14)得

$P_1=-\frac{2}{135}\left(1+\mu \right)\left(73\mu -173\right)W_0^3+\frac{2}{135}k\left(1+\mu \right)\left(82\mu -227\right)W_0^2-\frac{1}{36}{k}^2\left(1+\mu \right)\left(11\mu -35\right)W_0$ (25)

将(25)代入(24)，可得

$\begin{array}{c}{\phi }_1=\frac{1}{1440}{W}_0\left(\mu -1\right)(15k^2\left(3-10\rho +2{\rho }^2\right)\left(\mu -1\right)+2k{W}_0\left(217-255{\rho }^2\right)\left(\mu -1\right)\\ +45{\rho }^3\left(\mu -1\right)-137\mu +15\rho \left(35\mu -51\right))\\ +8W_0^2\left(111{\rho }^2\left(\mu -1\right)-39{\rho }^3\left(\mu -1\right)+6x^4\left(\mu -1\right)+38\mu -3\rho \left(53\mu -73\right)-58\right)\end{array}$

由(21)得

$\begin{array}{c}{S}_1=\frac{1}{120960}{W}_0\left(1+\mu \right)(-42W_0\left(7k^2-104k{W}_0+208W_0^2\right){\rho }^5\left(\mu -1\right)-408\left(k-4W_0\right)W_0^2{\rho }^6\left(\mu -1\right)\begin{array}{c}\\ \end{array}\\ -144W_0^3{\rho }^7\left(\mu -1\right)+21\left(k-4W_0\right)\rho \left(k{W}_0\left(434-274\mu \right)+45k^2\left(\mu -1\right)+16W_0^2\left(19\mu -29\right)\right)\\ +63{\rho }^4\left(-k^3\left(\mu -1\right)+48k^2{W}_0\left(\mu -1\right)+64W_0^3\left(7\mu -8\right)-8k{W}_0^2\left(41\mu -49\right)\right)\\ +14{\rho }^3\left(8W_0^3\left(607-467\mu \right)+15k^2{W}_0\left(59-51\mu \right)+45k^3\left(\mu -1\right)+8k{W}_0^2\left(428\mu -583\right)\right)\\ +7{\rho }^2(-195k^3\left(\mu -1\right)+\frac{1}{\mu -1}(14k^2{W}_0\left(65+124\mu -109{\mu }^2\right)+147k^3\left(\mu -1\right)\\ \begin{array}{c}\\ \end{array}-128W_0^3\left(34-74\mu +33{\mu }^2\right)+8k{W}_0^2\left(359-1218\mu +607{\mu }^2\right))))\end{array}$

依次求解这些边值问题，可求得 ${\phi }_2,S_2,{\phi }_3,S_3,\cdots$，则n项近似解为

$\phi \approx {\displaystyle {\sum }_{i=0}^n{\phi }_i}$

$S\approx {\displaystyle {\sum }_{i=0}^n{S}_i}$

3. 结果与讨论

首先二次近似解对应的该圆底扁薄球壳的特征方程，即无量纲载荷P二次近似为

$P\approx P_0+P_1$

由(23)和(25)可知P与 $W_0$ 的特征方程为

$P=-\frac{2}{135}\left(1+\mu \right)\left(73\mu -173\right)W_0^3+\frac{2}{135}k\left(1+\mu \right)\left(82\mu -227\right)W_0^2+\left(\frac{16}{3}-\frac{1}{36}{k}^2\left(1+\mu \right)\left(11\mu -35\right)\right)W_0$

在图1中根据本文结果绘出的 $k=2,6,16,20,26$ 对应的P-W₀曲线，其中取 $\mu =0.3$。这些特征曲线与文献 [7] 的特征曲线是一致的。

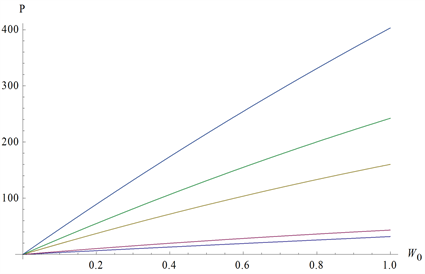
Figure 1. Characteristic curves P-W₀ under various k values (quadratic approximation)

图1. 各种k值下的特征曲线P-W₀ (二次近似)

因为无法得到该边值问题的精确解，所以我们使用如下余函数作为误差分析函数，分析得到的近似解。

$Error1=\frac{{\text{d}}^2}{\text{d}{\rho }^2}\left(\rho \cdot \phi \right)-3\left(1-{\mu }^2\right)\cdot S\cdot \phi -\frac{3}{4}P$

$Error2=\frac{{\text{d}}^2}{\text{d}{\rho }^2}\left(\rho \cdot S\right)+\frac{1}{2}\left[{\phi }^2-{\left(\frac{k}{2}\right)}^2\right]$

误差函数 $Error1$ 与 $Error2$ 在区间 $\rho \in \left(0,1\right)$ 上的曲线图在图2、图3中给出。本文中通过2-范数的平方 ${\Vert Error1\Vert }_2^2$ 与 ${\Vert Error2\Vert }_2^2$ 来表征近似解的精度。特取 $W_0=0.2$ 时，一阶、二阶、三阶近似解的误差分析如下表1所示。不难看出，随着阶数的增加，误差越来越小，进而说明了得到的结果的有效性。

Table 1. Precision of approximate solution with different orders

表1. 不同阶数下近似解的精度

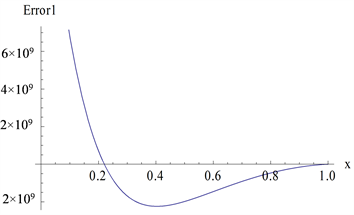
Figure 2. The curve of $Error1$ with $W_0=0.2$ (three approximation)

图2. $W_0=0.2$ 时， $Error1$ 曲线(三次近似)

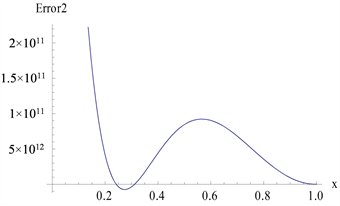
Figure 3. The curve of $Error2$ with $W_0=0.2$ (three approximation)

图3. $W_0=0.2$ 时， $Error2$ 曲线(三次近似)

基金项目

内蒙古自然科学基金(2020LH01003)，内蒙古工业大学重点学科团队(ZD202018)。