一类链环的HOMFLY多项式

The HOMFLY Polynomials of Class of Links

摘要: 纽结理论是研究绳圈(或多个绳圈)在连续变形下保持不变的特性，而纽结多项式指的是一类以多项式表达的纽结不变量。HOMFLY多项式是继Jones多项式之后，又一个计算纽结的重要的多项式。本文研究一类特殊的Brunnian链环，并给出这类链环的HOMFLY多项式。

Abstract: Knot theory studies the properties of rings (or multiple rings) remaining constant under continuous deformation, while knot polynomials refer to a class of knot invariants expressed in polynomials. The HOMFLY polynomial is another important polynomial after the Jones polynomial to calculate the knot. This paper deals with a special class of Brunnian links and gives their HOMFLY polynomials.

1. 前言

数学上的纽结理论是20世纪以来作为拓扑学的一个重要的部分而发展起来的。纽结理论是研究绳圈(或多个绳圈)在连续变形下保持不变的特性 [1]，纽结多项式指的是一类以多项式表达的纽结不变量。

本文研究一类特殊的Brunnian链环，给出了计算该链环的HOMFLY多项式的计算公式。一方面，通过利用HOMFLY多项式的拆接关系，得到 $B\left(0\right)$ 、 $B\left(0,0\right)$ 、 $B\left(0,0,0\right)$ 的HOMFLY多项式。另一方面，从 $B\left(0,0,\cdots ,0\right)$ 的拆接关系式组出发建立与 $B\left(0\right)$ 的关系。最后逐步递推给出计算 $B\left(0,0,\cdots ,0\right)$ 的HOMFLY多项式的计算公式。

2. 预备知识

2.1. 纽结

把单位圆周 $S^1$ 嵌入到球面 $S^3$ 或者三维欧式空间 $R^3$ 中得到纽结。设K是简单闭曲线，K在 $S^3$ 中且 $K\cong S^1$，则称K为一个纽结。

2.2. 链环

设链环 $L=K_1\cup K_2\cup \cdots \cup K_n$，即把若干个互不相交的圆周 $S_i^1\left(1\le i\le n,n\ge 1\right)$ 嵌入到球面 $S^3$ 或者三维欧式空间 $R^3$ 中，所形成的图形称为链环，其中 $K_i\left(i=1,2,\cdots ,n\right)$ 称为链环L的一个分支，n为链环L的分支数。

当 $K_i$ 都为平凡纽结，则L为平凡链环；当给定链环每个分支一个方向，则得到定向链环。

2.3. 投影图

选择一个合适的平面，将三维空间中的纽结正则投影到该平面上，满足：

1) 只有有限多个交叉点；

2) 每个交叉点都是二重点；

3) 在每个二重点位置，上下线处的投影都是互相穿越交叉的。

则称为纽结(链环)投影图。注意，由于平面的选择不同所得到的投影图也不唯一。

2.4. Reidemeister Move (R变换)

Reidemeister变换有三种改变方式可以改变纽结(链环)的正则投影图，分别是R1变换、R2变换、R3变换，且每一种都会改变交叉点之间的关系 [1]。如图1所示。

如果一个投影图经过一连串的R1、R2、R3变换，以及平面的变形，可以得到另一个投影图，则称两个投影图等价或者同痕。换句话说就是纽结(链环)在R1、R2、R3变换下保持不变。

2.5. 纽结连通和

对纽结 $K_1$ 和 $K_2$ 各取一个走向，将其放在一个平面的两侧，将它们的任意的一个小段拉向分隔平面，如图把它们在平面处走向互相协调的连通，得到原来两个有向纽结的和，称为连通和，记为。如图2所示。

Figure 1. Reidemeister move

图1. R变换

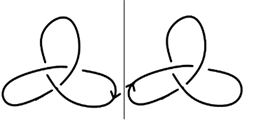K₁ K₂ K₁#K₂

Figure 2. The connected sum of $K_1$ and $K_2$

图2. $K_1$ 和 $K_2$ 的连通和

2.6. HOMFLY多项式

设 $L=K_1\cup K_2\cup \cdots \cup K_n$ 是 $S^3$ 中的可定向链环，存在一个对应的P，给每个可定向链环L的投影图联系上 $l,m$ 的整系数多项式 $P\left(L\right)$，满足一下二个条件 [2]：

1) 标准值：

平凡纽结O所对应的多项式是 $P\left({\rm O}\right)=1$。

2) 拆接关系式：

$lP\left(L_{+}\right)+l^{-1}P\left(L_{-}\right)+mP\left(L_0\right)=0.$

其中 $L_{+}$ 、 $L_{-}$ 、 $L_0$ 为三个可定向链环，且除了图3所示的部分其余相同。

L₊ L₋ L₀

Figure 3. Skein relation

图3. 拆接关系式

我们称 $P\left(L\right)$ 为L的HOMFLY多项式。

2.7. $B\left(0,0,\cdots ,0\right)$

定义1 Brunnian链环是一类特殊的n分支链环，即拆掉一个分支，剩下的分支为平凡链环，此性质的链环称为Brunnian链环 [3]。设 $B\left(0,0,\cdots ,0\right)$ 为可定向的n分支的Brunnian链环 [4]，每个分支给定同样的方向，且当 $n=1$ 时， $B\left(0,0,\cdots ,0\right)$ 变为 $B\left(0\right)$， $B\left(0\right)$ 是构成 $B\left(0,0,\cdots ,0\right)$ 的单位元素，如图4所示。

$B\left(0,0,\cdots ,0\right)$ $B(\; 0\; )$

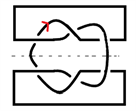
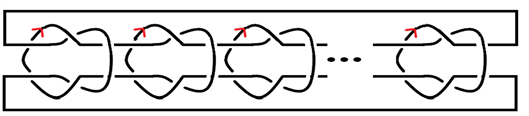
Figure 4. $B\left(0,0,\cdots ,0\right)$ and $B(\; 0\; )$

图4. $B\left(0,0,\cdots ,0\right)$ 和 $B(\; 0\; )$

3. $B\left(0,0,\cdots ,0\right)$ 的HOMFLY多项式计算

定理1 $B(\stackrel{n}{\stackrel{︷}{0,0,\cdots ,0}})={\displaystyle \underset{i=1}{\overset{i=n-1}{\sum }}{\alpha }^{n-i}{\left[\left(m^3-2m\right)\left(l^{-1}+l\right)\right]}^{i-1}}{\left(1-m^2\right)}^2+{\left[\left(m^3-2m\right)\left(l^{-1}+l\right)\right]}^{n-1}B\left(0\right)$。

证明：

1) 计算 $B(\; 0\; )$

设 ^{$T\left(s_i\right)$} 是一个排叉结 [5]，其中 $s_i$ 是具有 $i=n$ 个半扭转的横向排列，当 $s_i>0$ 时表示正的半扭转，当 $s_i<0$ 时表示负的半扭转。其中当 $i=0$ 时， $T\left(s_0\right)=-\left(l+l^{-1}\right)m^{-1}=\alpha$ ；当 $i=1$ 时， $T\left(s_1\right)=P\left({\rm O}\right)=1$。如图5所示。

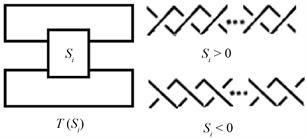
Figure 5. Pretzel link $T\left(s_i\right)$ and twists $s_i$

图5. 排叉结 $T\left(s_i\right)$ 和扭转 $s_i$

现把 $B\left(0\right)$ 的投影图看成两个排叉结 $T\left(s_3<0\right)$ 和 $T\left(s_3>0\right)$ 作连通和得到的，给定方向，如图6所示。

应用HOMFLY多项式的拆接关系，拆接 $T\left(s_3>0\right)$ 中半扭转的最右侧交叉点，整理可得：

$T\left(s_3>0\right)=-2l^2-l^4+m^2{l}^2$ (3.1)

而 $T\left(s_3<0\right)$ 的投影图是 $T\left(s_3>0\right)$ 投影图的镜像的反定向，将 $T\left(s_i>0\right)$ 的HOMFLY多项式中的 $l$ 替换为 $l^{-1}$ 可得到 $T\left(s_i<0\right)$，即：

$T\left(s_3<0\right)=-2l^{-2}-l^{-4}+m^2{l}^{-2}$ (3.2)

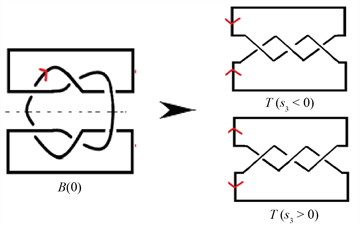
Figure 6. $T\left(s_3<0\right)$ and $T\left(s_3>0\right)$ are connected sum to get $B(\; 0\; )$

图6. $T\left(s_3<0\right)$ 和 $T\left(s_3>0\right)$ 作连通和得到 $B(\; 0\; )$

则

$B\left(0\right)=T\left(s_3>0\right)T\left(s_3<0\right)=\left(-2l^2-l^4+m^2{l}^2\right)\left(-2l^{-2}-l^{-4}+m^2{l}^{-2}\right)$ (3.3)

2) 计算 $B\left(0,0\right)$

按照HOMFLY多项式的拆接关系，我们将 $B\left(0,0\right)$ 拆接为方便计算的链环，如图7所示。

$B\left(0,0\right)$ $B\left(\ast \ast \right)$ $B(\; \ast \; )$

Figure 7. The skein relation of $B\left(0,0\right)$

图7. $B\left(0,0\right)$ 的拆接关系式

对 $B\left(0,0\right)$ 拆接右上角交叉点后得到 $B\left(\ast \ast \right)$ 和 $B(\ast )$ 两个链环，得到拆接关系式：

$lB\left(0,0\right)+l^{-1}B\left(\ast \ast \right)+mB(\ast )=0$ (3.4)

显然不容易直接计算，接下来拆接 $B\left(\ast \ast \right)$ 右下角交叉点，如图所示，可以得到经过Reidemeister变换后的 $T\left(s_0\right)$ 和 $B\left(0,-2\right)$ 两个链环，得到如图8所示的拆接关系式：

$B\left(\ast \ast \right)$ $T\left(s_0\right)$ $B\left(0,-2\right)$

Figure 8. The skein relation of $B(\; \ast \; \ast \; )$

图8. $B\left(\ast \ast \right)$ 的拆接关系式

$l^{-1}B\left(\ast \ast \right)+lT\left(s_0\right)+mB\left(0,-2\right)=0$ (3.5)

最后拆接 $B(\ast )$ 右上角交叉点，如图所示，我们可以得到经过Reidemeister变换后的 $B\left(0\right)\#T\left(s_3>0\right)$ 和 $B\left(\ast \ast \right)$ 两个链环，得到如图9所示的拆接关系式：

$B(\ast )$ $B\left(0\right)\#T\left(s_3>0\right)$ $B(\; \ast \; \ast \; )$

Figure 9. The skein relation of $B(\; \ast \; )$

图9. $B(\ast )$ 的拆接关系式

$lB(\ast )+l^{-1}B\left(0\right)T\left(s_3>0\right)+mB\left(\ast \ast \right)=0$ (3.6)

整理 $B\left(0,0\right)$ 的拆接关系式(3.4)~(3.6)得到方程组：

$\{\begin{array}{l}lB\left(0,0\right)+l^{-1}B\left(\ast \ast \right)+mB(\ast )=0\\ l^{-1}B\left(\ast \ast \right)+l\alpha +mB\left(0,-2\right)=0\\ lB(\ast )+l^{-1}B\left(0\right)T\left(s_3>0\right)+mB\left(\ast \ast \right)=0\end{array}$

化简方程组得到：

$B\left(0,0\right)=\alpha \left(1-m^2\right)+m{l}^{-3}B\left(0\right)T\left(s_3>0\right)+m{l}^{-1}\left(1-m^2\right)B\left(0,-2\right)$ (3.7)

3) 计算 $B\left(0,-2\right)$

按照拆接关系，拆接 $B\left(0,-2\right)$ 右下角的交叉点，得到如图10所示的拆接关系式：

$B\left(0,-2\right)$ $B\left(0\right)$ $T(\; s\; 0\; )$

Figure 10. The skein relation of $B\left(0,-2\right)$

图10. $B\left(0,-2\right)$ 的拆接关系式

$l^{-1}B\left(0,-2\right)+lB\left(0\right)+m\alpha =0$

则

$l^{-1}B\left(0,-2\right)=-lB\left(0\right)-m\alpha$

$B\left(0,-2\right)=-l^{2}B\left(0\right)-ml\alpha$ (3.8)

4) 计算 $B\left(0,0,0\right)$

按照2)中 $B\left(0,0\right)$ 的拆接方法，拆接右侧的交叉点，得到 $B\left(0,0,0\right)$ 的拆接关系式，整理关系式得到方程组：

$\{\begin{array}{l}lB\left(0,0,0\right)+l^{-1}B\left(0,\ast \ast \right)+mB\left(0,\ast \right)=0\\ l^{-1}B\left(0,\ast \ast \right)+l{\alpha }^2+mB\left(0,0,-2\right)=0\\ lB\left(0,\ast \right)+l^{-1}B\left(0,0\right)T\left(s_3>0\right)+mB\left(0,\ast \ast \right)=0\end{array}$

化简方程组得到：

$B\left(0,0,0\right)={\alpha }^2\left(1-m^2\right)+m{l}^{-3}B\left(0,0\right)T\left(s_3>0\right)+m{l}^{-1}\left(1-m^2\right)B\left(0,0,-2\right)$ (3.9)

5) 计算 $B\left(0,0,-2\right)$

按照3)中 $B\left(0,-2\right)$ 的拆接方法，同样拆接 $B\left(0,0,-2\right)$ 右侧的交叉点，得到 $B\left(0,0,-2\right)$ 的拆接关系式：

$l^{-1}B\left(0,0,-2\right)+lB\left(0,0\right)+m{\alpha }^2=0$

则

$l^{-1}B\left(0,0,-2\right)=-lB\left(0,0\right)-m{\alpha }^2$

$B\left(0,0,-2\right)=-l^{2}B\left(0,0\right)-ml{\alpha }^2$ (3.10)

6) 计算 $B\left(0,0,\cdots ,0\right)$

按照2)和4)中的方法，对 $B\left(0,0,\cdots ,0\right)$ 拆接右上角的交叉点后得到 $B\left(0,\cdots ,\ast \ast \right)$ 和 $B\left(0,\cdots ,\ast \right)$ 两个链环，得到如图11所示的拆接关系式：

$B\left(0,0,\cdots ,0\right)$ $B\left(0,\cdots ,\ast \ast \right)$ $B\left(0,\cdots ,\ast \right)$

Figure 11. The skein relation of $B\left(0,0,\cdots ,0\right)$

图11. $B\left(0,0,\cdots ,0\right)$ 的拆接关系式

$lB\left(0,0,\cdots ,0\right)+l^{-1}B\left(0,\cdots ,\ast \ast \right)+mB\left(0,\cdots ,\ast \right)=0$ (3.11)

拆接 $B\left(0,\cdots ,\ast \ast \right)$ 右下角交叉点，得到经过Reidemeister变换后的 $P\left({\rm O}\cup {\rm O}\cup \cdots \cup {\rm O}\right)$ 和 $B\left(0,\cdots ,-2\right)$，其中 $P\left({\rm O}\cup {\rm O}\cup \cdots \cup {\rm O}\right)={\alpha }^{n-1}$ 表示有n个平凡纽结并在一起的HOMFLY多项式，得到如图12所示的拆接关系式：

$B\left(0,\cdots ,\ast \ast \right)$ $P\left({\rm O}\cup {\rm O}\cup \cdots \cup {\rm O}\right)$ $B\left(0,\cdots ,0,-2\right)$

Figure 12. The skein relation of $B\left(0,\cdots ,\ast \ast \right)$

图12. $B\left(0,\cdots ,\ast \ast \right)$ 的拆接关系式

$l^{-1}B\left(0,\cdots ,\ast \ast \right)+l{\alpha }^{n-1}+mB\left(0,\cdots ,0,-2\right)=0$ (3.12)

最后拆接 $B(\ast )$ 右上角交叉点，如图所示，得到经过Reidemeister变换后的 $B\left(0,\cdots ,0\right)\#T\left(s_3>0\right)$ 和 $B\left(0,\cdots ,\ast \ast \right)$ 两个链环，其中 $B\left(0,\cdots ,0\right)\#T\left(s_3>0\right)$ 中的 $B\left(0,\cdots ,0\right)$ 是由 $n-1$ 个单位元素 $B\left(0\right)$ 构成，得到如图13所示的拆接关系式：

$B\left(0,\cdots ,\ast \right)$ $B\left(0,\cdots ,0\right)\#T\left(s_3>0\right)$ $B\left(0,\cdots ,\ast \ast \right)$

Figure 13. The skein relation of $B\left(0,\cdots ,\ast \right)$

图13. $B\left(0,\cdots ,\ast \right)$ 的拆接关系式

$lB\left(0,\cdots ,\ast \right)+l^{-1}B\left(0,\cdots ,0\right)\#T\left(s_3>0\right)+mB\left(0,\cdots ,\ast \ast \right)=0$ (3.13)

整理 $B\left(0,0,\cdots ,0\right)$ 的拆接关系式(3.11)~(3.13)，得到方程组：

$\{\begin{array}{l}lB\left(0,0,\cdots ,0\right)+l^{-1}B\left(0,\cdots ,\ast \ast \right)+mB\left(0,\cdots ,\ast \right)=0\\ l^{-1}B\left(0,\cdots ,\ast \ast \right)+l{\alpha }^{n-1}+mB\left(0,\cdots ,0,-2\right)=0\\ lB\left(0,\cdots ,\ast \right)+l^{-1}B\left(0,\cdots ,0\right)\#T\left(s_3>0\right)+mB\left(0,\cdots ,\ast \ast \right)=0\end{array}$

化简方程组得到：

$B(\stackrel{n}{\stackrel{︷}{0,0,\cdot \cdot \cdot ,0}})={\alpha }^{n-1}\left(1-m^2\right)+m{l}^{-3}B(\stackrel{n-1}{\stackrel{︷}{0,0,\cdot \cdot \cdot ,0}})T\left(s_3>0\right)+m{l}^{-1}\left(1-m^2\right)B(\stackrel{n-1}{\stackrel{︷}{0,\cdots ,0}},-2)$ (3.14)

其中 $B(\stackrel{n}{\stackrel{︷}{0,0,\cdot \cdot \cdot ,0}})$ 表示定义1中，n分支的Brunnian链环 $B\left(0,0,\cdots ,0\right)$。其中 $B(\stackrel{n-1}{\stackrel{︷}{0,\cdots ,0}},-2)$ 表示(3.12)拆接关系式中n − 1分支的Brunnian链环 $B\left(0,\cdots ,-2\right)$。而按照(3)和(5)的方法拆接 $B(\stackrel{n-1}{\stackrel{︷}{0,\cdots ,0}},-2)$ 右下角的交叉点，同理可得到：

$B(\stackrel{n-1}{\stackrel{︷}{0,\cdots ,0}},-2)=-l^{2}B(\stackrel{n-1}{\stackrel{︷}{0,0,\cdot \cdot \cdot ,0}})-ml{\alpha }^{n-1}$ (3.15)

把方程(3.1)和(3.15)代入(3.14)，得到：

$B(\stackrel{n}{\stackrel{︷}{0,0,\cdot \cdot \cdot ,0}})={\alpha }^{n-1}{\left(1-m^2\right)}^2+\left[\left(m^{-3}-2m\right)\left(l^{-1}+l\right)\right]B(\stackrel{n-1}{\stackrel{︷}{0,0,\cdot \cdot \cdot ,0}})$ (3.16)

显然观察方程(3.16) $B(\stackrel{n}{\stackrel{︷}{0,0,\cdot \cdot \cdot ,0}})$ 的HOMFLY多项式，可知 $B(\stackrel{n}{\stackrel{︷}{0,0,\cdot \cdot \cdot ,0}})$ 与 $B(\stackrel{n-1}{\stackrel{︷}{0,0,\cdot \cdot \cdot ,0}})$ 有关，继续按照(6)中拆接方法，拆接 $B(\stackrel{n-1}{\stackrel{︷}{0,0,\cdot \cdot \cdot ,0}})$ 得到的HOMFLY多项式，可知 $B(\stackrel{n-1}{\stackrel{︷}{0,0,\cdot \cdot \cdot ,0}})$ 与 $B(\stackrel{n-2}{\stackrel{︷}{0,0,\cdot \cdot \cdot ,0}})$ 有关，重复拆接操作直到得到 $B\left(0,0\right)$ 与 $B\left(0\right)$ 有关。因此按照递推的方法从 $B\left(0\right)$ 可以推出 $B(\stackrel{n}{\stackrel{︷}{0,0,\cdot \cdot \cdot ,0}})$ 的计算公式。

综合方程(3.1)~(3.16)，整理化简可以得到方程组：

$\{\begin{array}{l}B\left(0\right)=\left(-2l^2-l^4+m^2{l}^2\right)\left(-2l^{-2}-l^{-4}+m^2{l}^{-2}\right)\hfill \\ B\left(0,0\right)=\alpha {\left(1-m^2\right)}^2+\left[\left(m^{-3}-2m\right)\left(l^{-1}+l\right)\right]B\left(0\right)\hfill \\ B\left(0,0,0\right)={\alpha }^2{\left(1-m^2\right)}^2+\left[\left(m^{-3}-2m\right)\left(l^{-1}+l\right)\right]B\left(0,0\right)\hfill \\ ⋮\hfill \\ B(\stackrel{n}{\stackrel{︷}{0,0,\cdots ,0}})={\alpha }^{n-1}{\left(1-m^2\right)}^2+\left[\left(m^{-3}-2m\right)\left(l^{-1}+l\right)\right]B(\stackrel{n-1}{\stackrel{︷}{0,0,\cdots ,0}})\hfill \end{array}$ (3.17)

取 $X={\left(1-m^2\right)}^2$， $Y=\left(m^{-3}-2m\right)\left(l^{-1}+l\right)$，令 $a_1=B\left(0\right)$， $a_2=B\left(0,0\right)$， $\cdots$， $a_n=B(\stackrel{n}{\stackrel{︷}{0,0,\cdots ,0}})$，代入方程组(3.17)，整理得到通项公式：

$a_n={\displaystyle \underset{i=1}{\overset{i=n-1}{\sum }}{\alpha }^{n-i}}{Y}^{i-1}X+Y^{n-1}{a}_1$

综上所述，可以得到该类链环的HOMFLY多项式的计算公式，即

$B(\stackrel{n}{\stackrel{︷}{0,0,\cdots ,0}})={\displaystyle \underset{i=1}{\overset{i=n-1}{\sum }}{\alpha }^{n-i}{\left[\left(m^3-2m\right)\left(l^{-1}+l\right)\right]}^{i-1}}{\left(1-m^2\right)}^2+{\left[\left(m^3-2m\right)\left(l^{-1}+l\right)\right]}^{n-1}B(\; 0\; )$

得证。

4. 结论

本文针对一类特殊的Brunnian链环 $B\left(0,0,\cdots ,0\right)$，利用HOMFLY多项式的拆接关系式，从链环投影图交叉点出发，重复拆接操作直到得到 $B\left(0\right)$，按照递推的方法从 $B\left(0\right)$ 可以推出的 $B\left(0,0,\cdots ,0\right)$ 计算公式，因此得到一类特殊的Brunnian链环 $B\left(0,0,\cdots ,0\right)$ 的HOMFLY多项式计算公式。