混凝土中变扩散系数的时间分数阶氯离子扩散模型研究

Research on the Time-Fractional Diffusion Model of Chloride Ion with Variable Diffusion Coefficient in Concrete

摘要: 研究氯离子在混凝土中的扩散机理可以有针对性地对混凝土进行修护，从而有效地延长混凝土的耐久性。对于氯离子在混凝土中扩散的一维问题，首先基于Caputo分数阶导数建立了变扩散系数的时间分数阶扩散模型，结合L1算法得到了数值求解该模型的有限差分格式。随后，针对一个实例，利用已有实验数据和最小二乘原理优化了模型中不同暴露时间下分数阶导数的阶数；通过数据拟合得到了时间分数阶导数的阶数与暴露时间之间的关系，进而建立了混凝土中变扩散系数的时间变分数阶的氯离子扩散模型。

Abstract: Research on the diffusion mechanism of Chloride ion in concrete can be applied to repair concrete, which can effectively prolong the durability of concrete. This paper is focusing on one-dimensional diffusion of Chloride ion in concrete. Firstly, the time-fractional diffusion model of Chloride ion with variable diffusion coefficient in concrete is established based on Caputo fractional derivative, which is solved by the finite difference scheme combining with L1 algorithm. Next, the fractional derivative parameter on different exposure time is optimized by using the existing experimental data and the least square method in the model. At last, the relationship between the optimal fractional derivative parameter and the exposure time is fitted, which results in the time variable fractional diffusion model of Chloride ion with variable diffusion coefficient in concrete.

1. 引言

在现代建筑物的建造中，混凝土由于价格低、建筑综合效益好，且具有良好的耐冲击性、可塑性和耐火性等特点，成为了最普遍的施工材料，从而其耐久性和服役寿命成为备受关注的问题。针对目前的土木工程，混凝土结构的耐久性不容乐观，建筑物承载力不足、开裂等问题屡见不鲜 [1]。混凝土中的氯离子主要通过扩散作用、渗透作用、毛细管作用和电化学作用等侵入到混凝土和钢筋表面。通常，氯离子的侵蚀是几种侵入方式的组合。但是，许多情况下认为扩散是最主要的侵入方式 [2]。

许多研究人员基于整数阶导数的Fick第二扩散定律来描述氯离子的扩散行为，Buenfeld等 [3] 假定混凝土中的氯离子传输过程是一个非稳态的扩散过程，并提出了此过程的假设条件；Mangat等 [4] 将时间因素考虑到氯离子的扩散系数中，并给出扩散系数与时间的函数表达式：

$D=D_i{t}^{-m}$ (1)

式中D_i为t等于1个时间单位时的扩散系数， $t\ge 0$ ；m为时间依赖性常数。同年Thomas等 [5] 修正了该模型中D_i不可测的缺点，提出氯离子的扩散系数是时变函数的观点，并给出下式：

$D_t=D_0{\left(\frac{t_0}{t}\right)}^m$ (2)

式中D₀和D_t分别为扩散时间为t₀和t时混凝土的氯离子扩散系数， $t\ge 0$。Thomas给出的(2)式说明，t₀时测定混凝土的氯离子扩散系数为D₀。

近年来，研究人员发现分数阶微积分可以更简洁准确地描述具有历史记忆和空间全域相关性等复杂力学与物理现象的过程，因而基于分数阶导数的扩散模型开始受到关注。宦俊蒙 [6] 使用拉普拉斯变换法及Crump反演方法求解分数阶扩散方程的半解析解。Chen等 [7] 考虑了氯离子和混凝土之间会发生相互作用，从而导致一定比例的氯离子与混凝土结合，所以使用了朗缪尔等温线描述氯离子浓度。Wei等 [8] 建立了氯离子整数阶扩散模型和Caputo型氯离子时间分数阶扩散模型，并通过均方位移的方法近似得到扩散系数D_α。

本文将基于Caputo型分数阶导数，考虑形如(2)式的变扩散系数，对混凝土中氯离子扩散时间分数阶的一维模型进行研究。

2. 变扩散系数的时间分数阶扩散模型

2.1. 模型建立

基于Fick第二定律和Caputo型分数阶导数 [9]，考虑氯离子在混凝土中的一维扩散问题，建立变扩散系数的时间分数阶扩散模型，描述为：

$\{\begin{array}{l}\frac{{\partial }^{\alpha }C\left(x,t\right)}{\partial t^{\alpha }}=D_0{\left(\frac{t_0}{t}\right)}^m\frac{{\partial }^{2}C\left(x,t\right)}{\partial x^2},0<x<+\infty ,t>0\\ C\left(x,0\right)=C_0,0\le x\le +\infty \\ C\left(0,t\right)=C_s,t>0\\ C\left(+\infty ,t\right)=C_0,t>0\end{array}$ (3)

式中∂^α/∂t^α为Caputo型分数阶算子；x为侵蚀深度， $x\in \left[0,+\infty \right)$ ；t为混凝土结构中氯离子暴露于环境的时间， $t\ge 0$ ；C(x, t)表示t时刻x深处下的氯离子浓度；D₀和D_t分别为扩散时间为t₀和t时的扩散系数；α为分数阶导数的阶数， $0<\alpha \le \text{1}$ ；C_s为混凝土表面氯离子浓度；C₀为氯离子内部初始浓度；C₀和C_s是常数；m为时间依赖性常数。

2.2. 模型求解的有限差分格式

这里结合L1算法 [9]：

$\begin{array}{c}{D}_t^{\alpha }f\left(t_k\right)=\frac{\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}{\displaystyle \underset{s=0}{\overset{k-1}{\sum }}{\alpha }_s\left[f\left(t_{k-s}\right)-f\left(t_{k-s-1}\right)\right]}+O\left(\Delta t^{2-\alpha }\right)\\ =\frac{\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}\left[f\left(t_k\right)-{\alpha }_{k-1}f\left(t_0\right)-{\displaystyle \underset{s=1}{\overset{k-1}{\sum }}\left({\alpha }_{s-1}-{\alpha }_s\right)f\left(t_{k-s}\right)}\right]+O\left(\Delta t^{2-\alpha }\right)\end{array}$ (4)

其中 ${\alpha }_s={\left(s+1\right)}^{1-\alpha }-s^{1-\alpha },s=0,1,2,\cdots$，建立求解模型(3)的有限差分格式。

首先，选取足够大的空间长度L和暴露时间T。定义 $x=ih\left(i=0,\text{1},\cdots ,M\right)$， $t=k\tau \left(k=0,\text{1},\cdots ,N\right)$，其中h = L/M为空间步长，τ=T/N为时间步长。这样在划分求解区域后， $C_i^k$ 表示氯离子浓度在点(x_i , t_k)处的近似值。

接下来，将整数阶导数项在 $\left(x=x_i,t=t_{k-\frac{1}{2}}\right)$ 处离散：

$C|{}_{\left(x=x_i,t=t_{k-\frac{1}{2}}\right)}=\frac{C\left(x_i,t_k\right)+C\left(x_i,t_{k-1}\right)}{2}+O\left(\Delta t^2\right)$ (5)

$\frac{\partial C}{\partial x}|{}_{\left(x=x_i,t=t_{k-\frac{1}{2}}\right)}=\frac{C\left(x_i,t_k\right)-C\left(x_{i-1},t_k\right)+C\left(x_i,t_{k-1}\right)-C\left(x_{i-1},t_{k-1}\right)}{2\Delta x}+O\left(\Delta x\right)$， (6)

$\begin{array}{c}\frac{{\partial }^{2}C}{\partial x^2}|{}_{\left(x=x_i,t=t_{k-\frac{1}{2}}\right)}=\frac{C\left(x_{i+1},t_k\right)-2C\left(x_i,t_k\right)+C\left(x_{i-1},t_k\right)+C\left(x_{i+1},t_{k-1}\right)-2C\left(x_i,t_{k-1}\right)+C\left(x_{i-1},t_{k-1}\right)}{2\Delta x^2}\\ +O\left(\Delta x^2+\Delta t^2\right)\end{array}$ (7)

然后，将(4)~(7)代入扩散模型(3)，并用 $C_i^k$ 近似C(x_i, t_k)，得到有限差分格式：

$\begin{array}{l}{r}_1\left[\frac{C_i^k+C_i^{k-1}}{2}-{\alpha }_{k-1}\frac{C_i^1+C_i^0}{2}-{\displaystyle \underset{s=1}{\overset{k-1}{\sum }}\left({\alpha }_{s-1}-{\alpha }_s\right)\frac{C_i^{k-s}+C_i^{k-s-1}}{2}}\right]\\ =r_2\frac{C_{i+1}^k-2C_i^k+C_{i-1}^k+C_{i+1}^{k-1}-2C_i^{k-1}+C_{i-1}^{k-1}}{2}\left(i=1,2,\cdots ,M-1;k=1,2,\cdots ,N\right)\end{array}$ (8)

对应的初始条件和边界条件为：

$C_i^0=C_0\left(i=0,1,\cdots ,M\right)$ (9)

$C_0^k=C_s,C_M^k=C_0\left(k=1,2,\cdots ,N\right)$ (10)

其中 $r_1=\frac{h^2}{\Gamma \left(2-\alpha \right)}$， $r_2=D_0{\left[\frac{t_0}{\left(k-1\right)\tau }\right]}^m{\tau }^{\alpha }$。代入参数值，通过求解有限差分格式(8)~(10)，就可以得到变扩散系数的时间分数阶扩散模型的数值解。

3. 实例

Thomas等 [5] 进行了一系列氯离子扩散实验，所得的PC (混凝土预制件)中氯离子含量观测值如表1所示，各常数参数值如表2所示。

Table 1. Chloride concentration of Precast Concrete on different exposure time [5]

表1. PC不同暴露时间下的氯离子浓度值 [5]

Table 2. Initial concentration, surface concentration and values of parameters [5] [8]

表2. 初始浓度、表面浓度和参数值 [5] [8]

3.1. 固定分数阶导数的阶数

利用有限差分格式(8)~(10)，将表1和表2所提供的数据和参数值代入计算，就可以得到变扩散系数的时间分数阶扩散模型(3)在不同暴露时间下的氯离子浓度曲线。当取分数阶导数的阶数α = 0.9时，PC混凝土块在6个月、1~3年、6年和8年时的氯离子浓度曲线如图1(a)~(f)所示。图中绿色的数据点为实验数据 [5]，蓝色曲线为扩散模型(3)的数值解，数值解在一定程度上与实验数据一致，验证了模型的有效性。

3.2. 优化分数阶导数的阶数

为了更准确地反映氯离子的扩散行为，采用最小二乘法对分数阶导数的阶数α进行优化，也就是寻找α使得扩散模型的数值解与实验数据的误差的平方和Q达到最小值，即

$\underset{\alpha }{\min }Q=\underset{\alpha }{\min }{\displaystyle \underset{i=1}{\overset{5}{\sum }}{\left({C_i|}_{扩散模型数值解}-{C_i|}_{实验数据}\right)}^2}$ (11)

在不同暴露时间下，以精度0.0001的要求求解问题(11)，得到的结果如表3所示。可见，随着暴露时间的变化，最优的分数阶导数的阶数也在改变。利用表3中的结果，重新求解扩散模型(3)，得到了不同暴露时间下使用优化的分数阶导数的阶数α的氯离子浓度曲线，如图2(a)~(f)所示。

(a) 暴露6个月 (b) 暴露1年 (c) 暴露2年 (d) 暴露3年 (e) 暴露6年 (f) 暴露8年

Figure 1. Chloride ion concentration on different exposure time with α = 0.9

图1. 不同暴露时间下α = 0.9时氯离子浓度曲线

(a) 暴露6个月，α = 0.975 (b) 暴露1年，α = 0.956 (c) 暴露2年，α = 0.950 (d) 暴露3年，α = 0.941 (e) 暴露6年，α = 0.875 (f) 暴露8年，α = 0.890

Figure 2. Chloride ion concentration on different exposure time with optimal fractional derivative parameter α

图2. 不同暴露时间下优化的分数阶导数的阶数α的氯离子浓度曲线

Table 3. Optimal fractional derivative parameter α and the corresponding error square sum Q on different exposure time

表3. 不同暴露时间下最优阶数α和对应的误差平方和Q

3.3. 变扩散系数的时间变分数阶扩散模型

根据表3的结果，去除暴露时间为1年时的异常点后，采用三阶多项式拟合最优分数阶导数的阶数α与暴露时间t之间的关系，得到：

$\alpha \left(t\right)=0.0008t^3-0.0082t^2+0.0048t+0.9731$ (12)

拟合效果如图3所示。

Figure 3. Relationship between optimal fractional derivative parameter α and exposure time t

图3. 最优分数阶导数的阶数α与暴露时间t之间的关系

用(12)中的函数α(t)替换扩散模型(3)式中的分数阶导数的阶数α，就可以得到PC混凝土块的变扩散系数的氯离子时间变分数阶扩散模型：

$\{\begin{array}{l}\frac{{\partial }^{\alpha \left(t\right)}C\left(x,t\right)}{\partial t^{\alpha \left(t\right)}}=D_0{\left(\frac{t_0}{t}\right)}^m\frac{{\partial }^{2}C\left(x,t\right)}{\partial x^2},0<x<+\infty ,t>0\\ C\left(x,0\right)=C_0\cdot \delta \left(x\right),0\le x\le +\infty \\ C\left(0,t\right)=C_s,t>0\\ C\left(+\infty ,t\right)=C_0,t>0\end{array}$ (13)

式中 $0<\alpha \left(t\right)\le \text{1}$ 满足(12)。

3.4. 氯离子扩散浓度预测

当暴露时间分别为7年和9年时，对于扩散模型(3)选取α = 0.9计算氯离子浓度分布，如图4(a)和图4(b)中蓝色曲线所示。此时扩散模型(13)中的α(7) = 0.8748和α(9) = 0.9304，计算氯离子浓度如图4(a)和图4(b)中红色曲线所示。图4(a)中黑色星号为6年实验数据，图4(b)中绿色圆圈为8年实验数据。从图中不难看出，扩散模型(3)和扩散模型(13)都可以在一定程度上预测氯离子浓度的扩散情况，相比较而言扩散模型(13)更准确一些。

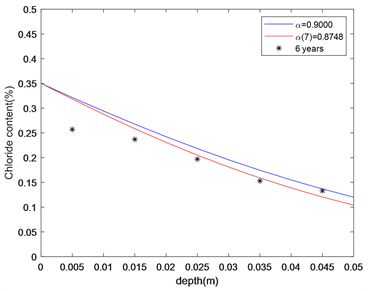(a) 暴露7年 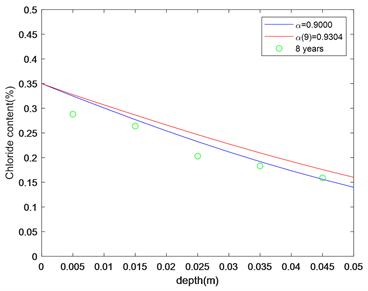(b) 暴露9年

Figure 4. Preditction of Chloride ion concentration when the exposure time t = 7 years and t = 9 years

图4. 暴露时间分别为7年和9年时氯离子浓度的预测值

4. 结论

· 变扩散系数的时间分数阶氯离子扩散模型可以有效地预测氯离子在混凝土中的扩散情况。

· 结合L1算法建立的有限差分格式实现了分数阶扩散模型的数值求解。

· 利用已有实验数据和最小二乘法优化了分数阶导数的阶数，进而建立了混凝土中变扩散系数的时间变分数阶氯离子扩散模型。

基金项目

北京市属高校基本科研业务费专项资金项目(X20142, X21027, X21030, X21031)，北京建筑大学教育科学研究项目(Y2015)，北京建筑大学研究生教学质量提升项目(J2020004)。

NOTES

^*通讯作者。