一类具双时滞的离散Nicholson果蝇模型的持久性和全局吸引性

Permanence and Global Attractivity of a Discrete Nicholson’s Blowflies Model with Two Delays

摘要: 本文考虑一类具有时滞和收获项的离散Nicholson果蝇模型，通过构造适当的Lyapunov函数，得到了系统持久性和全局吸引性的一些充分条件，最后用Matlab进行仿真，验证本文主要结论的正确性。

Abstract: In this paper, we consider a discrete Nicholson’s blowflies model with two delays. By constructing suitable Lyapunov functional, a sufficient condition for the permanence and global attractivity of the system is obtained. Numerical simulation shows the feasibility of our main results.

1. 引言

由于果蝇的生长周期很短，便于进行生物实验。因此，不论是在生物学方面，还是数学方面都相继出现了很多关于果蝇的讨论。20世纪80年代，Gurney [1] 首次提出了著名的Nicholson果蝇模型，此后，关于Nicholson果蝇模型的研究迅速发展，并已得到了一些很好的研究结果，如Chen [2] 考虑到外界环境周期性的变化，提出时滞周期型Nicholson苍蝇模型，得到了正周期解存在的一些充分条件；Yang [3] 研究了具有多时变时滞的广义Nicholson果蝇模型，利用一些微分不等式，证明了该模型的所有正解都指数收敛于零平衡点；Wang [4] 研究了一类具有多线性收获项的Nicholson果蝇模型正概周期解的存在性和指数收敛性；Berezansky [5] 等提出了一个带收获双时滞的微分方程模型，对于该模型，在文献 [6] [7] [8] 中已经得到了正平衡点的全局吸引性的相关结果，更多研究结果参见文献 [9] [10] [11] [12] [13]。

相对连续模型，离散模型的动力学性态更丰富也更复杂，许多无法求解或理论分析的连续模型往往需要离散模型进行数值模拟。关于离散的Nicholson模型正平衡点的振荡性、全局吸引性和概周期正解的存在性及指数收敛性等动力学性质得到了广泛地讨论 [14] [15] [16]。近年来，由于非自治离散模型能够更准确地刻画系统丰富且复杂的动力学性质，众多学者 [17] [18] [19] 把目光集中在非自治离散模型的研究上。本文基于文献 [5]，研究了一类具有收获项双时滞的离散非自治Nicholson果蝇模型的持久性和全局吸引性。

2. 预备知识

本文考虑下列具有双时滞的Nicholson果蝇离散模型

$x\left(n+1\right)-x\left(n\right)=-\alpha \left(n\right)x\left(n\right)+\beta \left(n\right)x\left(n-\tau \right)e^{-\gamma \left(n\right)x\left(n-\tau \right)}-h\left(n\right)x\left(n-\sigma \right),$ (2.1)

初值函数为 $x\left(k\right)=\phi \left(k\right)>0,k\in \left[-{\tau }^{*},0\right],{\tau }^{*}=\max \left\{\tau ,\sigma \right\}$ (2.2)

其中， $\alpha \left(n\right)$ 为第n代成虫平均死亡率， $\tau$ 为成长期， $\beta \left(n\right)$ 为第n代按种群数量计算平均产卵率的最大值， $1/\gamma \left(n\right)$ 为第n代以最大产卵率繁殖的种群数量， $h\left(n\right)$ 为第n代的收获率， $\sigma$ 为成熟期。从可持续经济的角度出发，幼体应该不在捕捞范围内，模型(2.1)考虑到捕捞项，引入了一个具时滞的线性函数 $h\left(n\right)x\left(n-\sigma \right)$。

首先，我们假设下列条件(H₁) (H₂)成立

(H₁) $\left\{\alpha \left(n\right)\right\},\left\{\beta \left(n\right)\right\},\left\{\gamma \left(n\right)\right\},\left\{h\left(n\right)\right\}$ 都是有界非负序列，且

$0<{\alpha }^l<{\alpha }^u<1,0<{\beta }^l<{\beta }^u,0<{\gamma }^l<{\gamma }^u,0<h^l<h^u<1,{\alpha }^u+h^u<1.$

(H₂) 存在两个正常数 $d_1>d_2>0$，使得

$d_1\ge \frac{{\beta }^u}{{\alpha }^l{\gamma }^{l}e},\frac{1}{{\gamma }^u}\le d_2\le \frac{{\beta }^l}{{\alpha }^u}{d}_1{e}^{-{\gamma }^u{d}_1}-\frac{h^u}{{\alpha }^u}{d}_1.$

其中，对任意有界序列 $\left\{f\left(n\right)\right\}$，定义 $f^l={\inf }_{k\in Z}f\left(k\right),f^u={\sup }_{k\in Z}f\left(k\right)$。

引理 2.1 [20] 若 $A>0,y\left(0\right)>0$，且

1) 若 $y\left(n+1\right)\le Ay\left(n\right)+B\left(n\right),n=1,2,\cdots$，则对任意正整数 $k\le n$ 有，

$y\left(n\right)\le A^{k}y\left(n-k\right)+{\displaystyle \underset{i=0}{\overset{k-1}{\sum }}{A}^{i}B}\left(n-i-1\right),n=1,2,\cdots .$

特别地，当 $A<1$，B有上确界M时，则

$\underset{n\to \infty }{\lim }\sup y\left(n\right)\le \frac{M}{1-A}.$

2) 若 $y\left(n+1\right)\ge Ay\left(n\right)+B\left(n\right),n=1,2,\cdots$，则对任意正整数 $k\le n$ 有，

$y\left(n\right)\ge A^{k}y\left(n-k\right)+{\displaystyle \underset{i=0}{\overset{k-1}{\sum }}{A}^{i}B}\left(n-i-1\right),n=1,2,\cdots .$

特别地，当 $A<1$，B有下确界m时，则

$\underset{n\to \infty }{\lim }\sup y\left(n\right)\ge \frac{m}{1-A}.$

引理2.2 若 $x\left(n\right)$ 是方程(2.1)在初值条件(2.2)下的任意解，则

$\underset{n\to \infty }{\lim }\sup x\left(n\right)\le M,M=\frac{{\beta }^u}{{\alpha }^l{\gamma }^{l}e}.$

证明：由方程(2.1)可得

$\begin{array}{l}x\left(n+1\right)=\left(1-\alpha \left(n\right)\right)x\left(n\right)+\beta \left(n\right)x\left(n-\tau \right)e^{-\gamma \left(n\right)x\left(n-\tau \right)}-h\left(n\right)x\left(n-\sigma \right)\\ \le \left(1-\alpha \left(n\right)\right)x\left(n\right)+{\beta }^{u}x\left(n-\tau \right)e^{-{\gamma }^{l}x\left(n-\tau \right)}.\end{array}$

根据 $\underset{u>0}{\sup }u{e}^{-\gamma u}=\frac{1}{\gamma e}$，可以得到

$x\left(n+1\right)\le \left(1-\partial \left(n\right)\right)x\left(n\right)+\frac{{\beta }^u}{{\gamma }^{l}e}.$ (2.3)

对于式(2.3)，由引理2.1可得

$\underset{n\to \infty }{\lim }\sup x\left(n\right)\le \frac{{\beta }^u}{{\alpha }^l{\gamma }^{l}e}\stackrel{def}{=}M.$

证毕。

引理2.3 [16] 令 $S_0=\left\{\phi |d_2<\phi \left(k\right)<d_1,\forall k\in \left[-{\tau }^{*},0\right]\right\},{\tau }^{*}=\text{max}\left\{\tau ,\sigma \right\}$，那么方程(2.1)在初值函数 $\phi \in S_0$ 下的任意解 $x\left(k\right)$ 满足 $d_2<x\left(k\right)<d_1,k\in Z^{+}$。

3. 持久性和全局吸引性

定理3.1 若条件(H₁)，(H₂)成立，那么具有初值函数 $\phi \in S_0$ 的系统(2.1)是持久的，即存在常数 $M,m>0$，使系统(2.1)的任意正解 $x\left(n\right)$ 满足

$m\le \underset{n\to \infty }{\lim }\inf x\left(n\right)\le \underset{n\to \infty }{\lim }\sup x\left(n\right)\le M.$

证明：由引理2.2、引理2.3可以得到

$\underset{n\to \infty }{\lim }\sup x\left(n\right)\le M=\frac{{\beta }^u}{{\alpha }^l{\gamma }^{l}e},\underset{n\to \infty }{\lim }\inf x\left(n\right)>0.$

接下来，只需证明存在正常数m使得 ${\lim }_{n\to \infty }\inf x\left(n\right)\ge m$，

令

$\eta =\underset{n\to \infty }{\lim }\inf x\left(n\right),G=\min \left\{g\left(\eta \right),g\left(M\right)\right\},g\left(x\right)=x{e}^{-{\gamma }^{u}x},$

由方程(2.1)和 $0<{\alpha }^u<1$ 可以得到

$\eta =\underset{n\to \infty }{\lim }\inf x\left(n\right)\ge \left[\left(\frac{x\left(0\right)+{\beta }^{l}G}{1+h^u}\right){\left(1-{\alpha }^u\right)}^n+\frac{{\beta }^{l}G}{{\alpha }^u\left(1+h^u\right)}\right]=\frac{{\beta }^{l}G}{{\alpha }^u\left(1+h^u\right)},$

如果 $G=g\left(\eta \right)$，那么

$\eta \ge \frac{{\beta }^l}{{\alpha }^u\left(1+h^u\right)}\eta e^{-{\gamma }^u\eta },$

即

$\eta \ge \frac{1}{{\gamma }^u}\ln \frac{{\beta }^l}{{\alpha }^u\left(1+h^u\right)},$

如果 $G=g\left(M\right)$，那么

$\eta \ge \frac{{\beta }^l}{{\alpha }^u\left(1+h^u\right)}M{e}^{-{\gamma }^{u}M}.$

则

$\underset{n\to \infty }{\lim }\inf x\left(n\right)\ge \min \left\{\frac{1}{{\gamma }^u}\ln \frac{{\beta }^l}{{\alpha }^u\left(1+h^u\right)},\frac{{\beta }^l}{{\alpha }^u\left(1+h^u\right)}M{e}^{-{\gamma }^{u}M}\right\}\stackrel{def}{=}m.$

证毕。

定理3.2 若条件(H₁)，(H₂)成立，且 ${\gamma }^{l}m>1$ 成立，那么具有初值函数 $\phi \in S_0$ 的系统(2.1)是全局吸引的，

即对系统(2.1)的任意解 $x\left(n\right),y\left(n\right)$ 有， $\underset{n\to \infty }{\lim }\left(x\left(n\right)-y\left(n\right)\right)=0$。

证明：由定理3.1可得

$m\le \underset{n\to \infty }{\lim }\inf x\left(n\right)\le \underset{n\to \infty }{\lim }\sup x\left(n\right)\le M,m\le \underset{n\to \infty }{\lim }\inf y\left(n\right)\le \underset{n\to \infty }{\lim }\sup y\left(n\right)\le M.$

对任意足够小的正常数 $\epsilon$，存在一个正整数 $n_0$，使得对任意 $n\ge n_0$，

$m\le x\left(n\right),y\left(n\right)\le M,$ (3.1)

由均值定理可以得到

$x\left(n\right)e^{-x\left(n\right)}-y\left(n\right)e^{-y\left(n\right)}=\left(1-\theta \left(n\right)\right)e^{-\theta \left(n\right)}\left(x\left(n\right)-y\left(n\right)\right),x\left(n\right)<\theta \left(n\right)<y\left(n\right).$ (3.2)

令

$w\left(n\right)=x\left(n\right)-y\left(n\right)+{\displaystyle \underset{s=n-\tau }{\overset{n-1}{\sum }}\beta \left(s+\tau \right)\left(x\left(s\right)e^{-\gamma \left(s+\tau \right)x\left(s\right)}-y\left(s\right)e^{-\gamma \left(s+\tau \right)y\left(s\right)}\right)}-{\displaystyle \underset{s=n-\sigma }{\overset{n-1}{\sum }}\beta \left(s+\sigma \right)\left(x\left(s\right)-y\left(s\right)\right)},$

则

$\begin{array}{c}w\left(n+1\right)=\left(1-\alpha \left(n\right)\right)\left(x\left(n\right)-y\left(n\right)\right)+\beta \left(n\right)\left(x\left(n-\tau \right)e^{-\gamma \left(n\right)x\left(n-\tau \right)}-y\left(n-\tau \right)e^{-\gamma \left(n\right)y\left(n-\tau \right)}\right)\\ -h\left(n\right)\left(x\left(n-\sigma \right)-y\left(n-\sigma \right)\right)+{\displaystyle \underset{s=n-\tau +1}{\overset{n}{\sum }}\beta \left(s+\tau \right)\left(x\left(s\right)e^{-\gamma \left(s+\tau \right)x\left(s\right)}-y\left(s\right)e^{-\gamma \left(s+\tau \right)y\left(s\right)}\right)}\\ -{\displaystyle \underset{s=n-\sigma +1}{\overset{n}{\sum }}\beta \left(s+\sigma \right)}\left(x\left(s\right)-y\left(s\right)\right),\end{array}$

$\begin{array}{c}\Delta w\left(n\right)=w\left(n+1\right)-w\left(n\right)\\ =-\alpha \left(n\right)\left(x\left(n\right)-y\left(n\right)\right)+\beta \left(n+\tau \right)\left(x\left(n\right)e^{-\gamma \left(n+\tau \right)x\left(n\right)}-y\left(n\right)e^{-\gamma \left(n+\tau \right)y\left(n\right)}\right)\\ -h\left(n+\sigma \right)\left(x\left(n\right)-y\left(n\right)\right).\end{array}$

构造非负函数 $V\left(n\right)=w^2\left(n\right)$，则

(3.3)

由(3.2)、(3.3)可得

$\begin{array}{l}\Delta V\left(n\right)\\ =-\left(\alpha \left(n\right)+h\left(n+\sigma \right)\right)\left(2-\alpha \left(n\right)-h\left(n+\sigma \right)\right){\left(x\left(n\right)-y\left(n\right)\right)}^2\\ +2\left(1-\alpha \left(n\right)-h\left(n+\sigma \right)\right)\beta \left(n+\tau \right)\left(1-\theta \left(n\right)\gamma \left(n+\tau \right)\right)e^{-\theta \left(n\right)\gamma \left(n+\tau \right)}{\left(x\left(n\right)-y\left(n\right)\right)}^2\\ +2\left(\alpha \left(n\right)+h\left(n+\sigma \right)\right)\left(x\left(n\right)-y\left(n\right)\right){\displaystyle \underset{s=n-\tau }{\overset{n-1}{\sum }}\beta \left(s+\tau \right)\left(1-\theta \left(s\right)\gamma \left(s+\tau \right)\right)e^{-\theta \left(s\right)\gamma \left(s+\tau \right)}\left(x\left(s\right)-y\left(s\right)\right)}\\ +{\left(\beta \left(n+\tau \right)\left(1-\theta \left(n\right)\gamma \left(n+\tau \right)\right)e^{-\theta \left(n\right)\gamma \left(n+\tau \right)}\left(x\left(n\right)-y\left(n\right)\right)\right)}^2\\ +2\beta \left(n+\tau \right)\left(1-\theta \left(n\right)\gamma \left(n+\tau \right)\right)e^{-\theta \left(n\right)\gamma \left(n+\tau \right)}\left(x\left(n\right)-y\left(n\right)\right)\\ \cdot {\displaystyle \underset{s=n-\tau }{\overset{n-1}{\sum }}\beta \left(s+\tau \right)\left(1-\theta \left(s\right)\gamma \left(s+\tau \right)\right)e^{-\theta \left(s\right)\gamma \left(s+\tau \right)}\left(x\left(s\right)-y\left(s\right)\right)}\\ +2\left(\alpha \left(n\right)+h\left(n+\sigma \right)\right)\left(x\left(n\right)-y\left(n\right)\right){\displaystyle \underset{s=n-\sigma }{\overset{n-1}{\sum }}h\left(s+\sigma \right)\left(x\left(s\right)-y\left(s\right)\right)}\\ -2\beta \left(n+\tau \right)\left(1-\theta \left(n\right)\gamma \left(n+\tau \right)\right)e^{-\theta \left(n\right)\gamma \left(n+\tau \right)}\left(x\left(n\right)-y\left(n\right)\right)\cdot {\displaystyle \underset{s=n-\sigma }{\overset{n-1}{\sum }}h\left(s+\sigma \right)\left(x\left(s\right)-y\left(s\right)\right).}\end{array}$ (3.4)

将 $2ab\le a^2+b^2$ 运用到式(3.4)得

$\begin{array}{l}\Delta V\left(n\right)\le -\left(\alpha \left(n\right)+h\left(n+\sigma \right)\right)\left(2-\alpha \left(n\right)-h\left(n+\sigma \right)\right){\left(x\left(n\right)-y\left(n\right)\right)}^2\\ +2\left(1-\alpha \left(n\right)-h\left(n+\sigma \right)\right)\beta \left(n+\tau \right)\left(1-\theta \left(n\right)\gamma \left(n+\tau \right)\right)e^{-\theta \left(n\right)\gamma \left(n+\tau \right)}{\left(x\left(n\right)-y\left(n\right)\right)}^2\\ +\left(\alpha \left(n\right)+h\left(n+\sigma \right)\right){\displaystyle \underset{s=n-\tau }{\overset{n-1}{\sum }}\beta \left(s+\tau \right)\left(1-\theta \left(s\right)\gamma \left(s+\tau \right)\right)e^{-\theta \left(s\right)\gamma \left(s+\tau \right)}{\left(x\left(n\right)-y\left(n\right)\right)}^2}\\ +\left(\alpha \left(n\right)+h\left(n+\sigma \right)\right){\displaystyle \underset{s=n-\tau }{\overset{n-1}{\sum }}\beta \left(s+\tau \right)\left(1-\theta \left(s\right)\gamma \left(s+\tau \right)\right)e^{-\theta \left(s\right)\gamma \left(s+\tau \right)}{\left(x\left(s\right)-y\left(s\right)\right)}^2}\text{}\\ +{\left(\beta \left(n+\tau \right)\left(1-\theta \left(n\right)\gamma \left(n+\tau \right)\right)e^{-\theta \left(n\right)\gamma \left(n+\tau \right)}\left(x\left(n\right)-y\left(n\right)\right)\right)}^2\\ +\beta \left(n+\tau \right)\left(1-\theta \left(n\right)\gamma \left(n+\tau \right)\right)e^{-\theta \left(n\right)\gamma \left(n+\tau \right)}\\ \cdot ({\displaystyle \underset{s=n-\tau }{\overset{n-1}{\sum }}\beta \left(s+\tau \right)\left(1-\theta \left(s\right)\gamma \left(s+\tau \right)\right)e^{-\theta \left(s\right)\gamma \left(s+\tau \right)}{\left(x\left(n\right)-y\left(n\right)\right)}^2}\\ +{\displaystyle \underset{s=n-\tau }{\overset{n-1}{\sum }}\beta \left(s+\tau \right)\left(1-\theta \left(s\right)\gamma \left(s+\tau \right)\right)e^{-\theta \left(s\right)\gamma \left(s+\tau \right)}{\left(x\left(s\right)-y\left(s\right)\right)}^2})\\ +\left(\alpha \left(n\right)+h\left(n+\sigma \right)\right){\displaystyle \underset{s=n-\sigma }{\overset{n-1}{\sum }}h\left(s+\sigma \right){\left(x\left(n\right)-y\left(n\right)\right)}^2}\\ +\left(\alpha \left(n\right)+h\left(n+\sigma \right)\right){\displaystyle \underset{s=n-\sigma }{\overset{n-1}{\sum }}h\left(s+\sigma \right){\left(x\left(s\right)-y\left(s\right)\right)}^2}\\ +\beta \left(n+\tau \right)\left(1-\theta \left(n\right)\gamma \left(n+\tau \right)\right)e^{-\theta \left(n\right)\gamma \left(n+\tau \right)}{\displaystyle \underset{s=n-\sigma }{\overset{n-1}{\sum }}h\left(s+\sigma \right){\left(x\left(n\right)-y\left(n\right)\right)}^2}\\ +\beta \left(n+\tau \right)\left(1-\theta \left(n\right)\gamma \left(n+\tau \right)\right)e^{-\theta \left(n\right)\gamma \left(n+\tau \right)}{\displaystyle \underset{s=n-\sigma }{\overset{n-1}{\sum }}h\left(s+\sigma \right){\left(x\left(s\right)-y\left(s\right)\right)}^2}.\end{array}$ (3.5)

依据 ${\gamma }^{l}m>1,{\alpha }^u+h^u<1,\underset{x\in \left[1,+\infty \right)}{\max }\left(1-x\right)e^{-x}<0$，不等式(3.5)可写成

$\begin{array}{l}\Delta V\left(n\right)\le -\left(\alpha \left(n\right)+h\left(n+\sigma \right)\right)\left(2-\alpha \left(n\right)-h\left(n+\sigma \right)\right){\left(x\left(n\right)-y\left(n\right)\right)}^2\\ \le -\left({\alpha }^u+h^u\right)\left(2-{\alpha }^u-h^u\right){\left(x\left(n\right)-y\left(n\right)\right)}^2\\ \le -\delta {\left(x\left(n\right)-y\left(n\right)\right)}^2.\end{array}$

取一个足够小的正常数 $\delta >0$ 使得

$\left({\alpha }^u+h^u\right)\left(2-{\alpha }^u-h^u\right)\le \delta ,$

则

$\Delta V\left(n\right)\le -\delta {\left(x\left(n\right)-y\left(n\right)\right)}^2.$ (3.6)

将不等式(3.6)左右两边分别从 $n_0+\tau$ 累加到n可得

${\displaystyle \underset{s=n_0+\tau }{\overset{n}{\sum }}\left(V\left(s+1\right)-V\left(s\right)\right)}\le -\delta {\displaystyle \underset{s=n_0+\tau }{\overset{n}{\sum }}{\left(x\left(s\right)-x\left(s\right)\right)}^2},$

即

$V\left(n+1\right)+\delta {\displaystyle \underset{s=n_0+\tau }{\overset{n}{\sum }}{\left(x\left(s\right)-x\left(s\right)\right)}^2}\le V\left(n_0+\tau \right),$

则

${\displaystyle \underset{s=n_0+\tau }{\overset{n}{\sum }}{\left(x\left(s\right)-x\left(s\right)\right)}^2}\le \frac{V\left(n_0+\tau \right)}{\delta }.$

由(3.1)可知 $V\left(n_0+\tau \right)$ 是有界的，因此

${\displaystyle \underset{s=n_0+\tau }{\overset{n}{\sum }}{\left(x\left(s\right)-x\left(s\right)\right)}^2}\le \frac{V\left(n_0+\tau \right)}{\delta }<+\infty ,$

也就是说

${\displaystyle \underset{s=n_0+\tau }{\overset{+\infty }{\sum }}{\left(x\left(s\right)-x\left(s\right)\right)}^2}\le \frac{V\left(n_0+\tau \right)}{\delta }<+\infty .$

显而易见， $\underset{n\to \infty }{\lim }{\left(x\left(n\right)-y\left(n\right)\right)}^2=0$，即 $\underset{n\to \infty }{\lim }\left(x\left(n\right)-y\left(n\right)\right)=0$。

证毕。

4. 数值模拟

考虑下列方程

$\begin{array}{l}x\left(n+1\right)-x\left(n\right)=-\left(0.5+0.01\sin \left(\sqrt{2}n\right)\right)x\left(n\right)+\left(2.79+0.01\sin \left(\sqrt{3}n\right)\right)x\left(n-1\right)\\ \cdot e^{-\left(0.82+0.01\sin n)x\left(n-1\right)\right)}-\left(0.2+0.01\sin \sqrt{2}n\right)x\left(n-1\right)\end{array}$ (4.1)

初始条件为

$x\left(-1\right)=1.4,x\left(0\right)=1.6$

其中，

$\begin{array}{l}{\alpha }^u=0.51,{\alpha }^l=0.49,{\beta }^u=2.8,{\beta }^l=2.78,{\gamma }^u=0.83,{\gamma }^l=0.81,h^u=0.21,\\ h^l=0.19,M=2.25,m=1.56,{\alpha }^u+h^u<1,{\gamma }^{l}m\approx 1.26>1.\end{array}$

$\begin{array}{l}x\left(n+1\right)-x\left(n\right)=-\left(0.5+0.02\sin \left(\sqrt{2}n\right)\right)x\left(n\right)+\left(2.79+0.02\sin \left(\sqrt{3}n\right)\right)x\left(n-1\right)\\ \cdot e^{-\left(0.82+0.02\sin n)x\left(n-1\right)\right)}-\left(0.2+0.02\sin \sqrt{2}n\right)x\left(n-1\right)\end{array}$ (4.2)

初始条件为

$x\left(-1\right)=1.3,x\left(0\right)=1.4$

$\begin{array}{l}x\left(n+1\right)-x\left(n\right)=-\left(0.51+0.02\sin \left(\sqrt{2}n\right)\right)x\left(n\right)+\left(2.80+0.02\sin \left(\sqrt{3}n\right)\right)x\left(n-1\right)\\ \cdot e^{-\left(0.80+0.02\sin n)x\left(n-1\right)\right)}-\left(0.21+0.02\sin \sqrt{2}n\right)x\left(n-1\right)\end{array}$ (4.3)

初始条件为

$x\left(-1\right)=1.5,x\left(0\right)=1.4$

$\begin{array}{l}x\left(n+1\right)-x\left(n\right)=-\left(0.51+0.01\sin \left(\sqrt{2}n\right)\right)x\left(n\right)+\left(2.80+0.02\sin \left(\sqrt{3}n\right)\right)x\left(n-1\right)\\ \cdot e^{-\left(0.82+0.01\sin n)x\left(n-1\right)\right)}-\left(0.21+0.02\sin \sqrt{2}n\right)x\left(n-1\right)\end{array}$ (4.4)

初始条件为

$x\left(-1\right)=1.3,x\left(0\right)=1.5$

显然，上述系统均满足条件(H₁)，(H₂) (H₃)，依据定理3.1和定理3.2，系统(4.1)、(4.2)、(4.3)、(4.4)的解 $x\left(n\right)$ 是持久且全局吸引的的(如图1)。

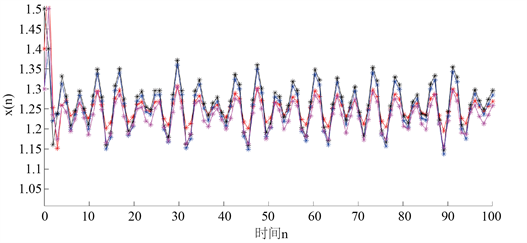
Figure 1. Dynamic behavior of solutions of systems

图1. 系统(4.1)、(4.2)、(4.3)、(4.4)解 $x\left(n\right)$ 的动态行为

5. 结论

本文考虑了具有时滞和收获项的离散非自治Nicholson果蝇模型。对于该模型，通过构造适当的Lyapunov函数，我们得到了它的持久性和全局吸引性存在的充分条件，并通过Matlab数值模拟充分验证了结果。

NOTES

^*通讯作者。