基于CUDA的多导体传输线方程迭代QR分解的并行算法

Parallelization of QR Decomposition Algorithm in Multiconductor Transmission Line Equation Based on CUDA

摘要: 基于电报方程发展的多导体传输线方程，随着导线的数量和复杂性的增加，导体的特征阻抗矩阵和导纳矩阵以及加上外部激励分布源向量的维数变得很大，从而使得求解由多导体传输线组成的电缆上的电压或电流的计算量和内存开销很大。本文考虑了有损导体和有损介质的一般情况，给出了基于CUDA的特征阻抗矩阵和导纳矩阵的迭代QR方法的并行化方法。为了证明我们的方法的有效性，我们评估了三种不同类型的实现类型：传统的单线程C++，使用OpenMP加速的C++和NvidiaCUDA。评估结果表明，当问题的维度达到数百个时，CUDA的GPU实现明显比单线程C++和OpenMP的CPU实现更有效。

Abstract: Based on the multi-conductor transmission line equation developed from the telegraph equation, as the number and complexity increase, the characteristic impedance matrix and conduction matrix and the dimension of the external excitation distribution source vector become large, resulting in the computational amount and memory overhead of solving the voltage or current on the cable composed of multi-conductor transmission lines. In this paper, we consider the general case of lossy conductor and lossy dielectric, and present the parallelization of iterative QR method for a matrix multiplied by the characteristic impedance matrix and admittance matrix based on CUDA. To prove the effectiveness of our method, we evaluate three different types of implementations: traditional single-thread C++, C++ accelerated with OpenMP and NvidiaCUDA. The evaluation result suggests that when the dimensions of problem reach hundreds, GPU implementation of CUDA is significantly more effective than CPU implementations of single-thread C++ and OpenMP.

1. 引言

具有N条平行导体和一条与之平行的参考导体组成的N-线多导体传输线，是组成复杂电子系统的基本电路单元形式之一。求解这样的多导体传输线上传播的电压波与电流，有许多学者进行了研究。Carl E. Baum、T. K. Liu与F. M. Tesche在文献 [1] 中以正实矩阵的特征模展开方法给出了有损导体与有耗介质一般情形下的解法，但没有给出特征值与特征向量的具体计算方法。文献 [2] 给出了多导体传输线问题的一种数值解方法。C. R. Paul在 [3] 中详细讨论了在没有外加激励源情形下多导体传输线电压与电流传播方程在导体无损与有损，介质无耗与有耗情形下的解，而对于导体有损与介质有耗的一般情形，只详细讨论了导体循环对称排列的特殊情形。F. M. Tesche与M. V. Ianoz和T. Karlsson详细介绍了在无耗介质情形下的多导体传输线上电压与电流传播方程的解 [4]。F. M. Tesche、J. Keen和C. M. Butler在 [5] 中给出了用BLT方程计算电磁场传播与耦合的实例。L. Paletta、J.-P. Parmantier等在文献 [6] 中将电磁场–传输线耦合模型应用于大型电缆系统分析。

多导体传输线上控制电压与电流传播的方程基于双导线的电报方程发展而来。但多导体传输线与双导体传输线有两个不同之处：一是在双导体传输线中为消除终端反射，只需使终端负载阻抗等于导体的特征阻抗即可。但在多导体传输线问题中，必需考虑特征阻抗矩阵，且一般为非对角矩阵。二是N条导体与参考导体之间的电容和电导也形成矩阵关系，因此，在有损导体与有耗介质情形导纳矩阵也是非对角矩阵。随着导体的数量增加，使得多导体传输线方程中特征阻抗矩阵和导纳矩阵的维数变得很大。而求解多导体传输线方程，需要计算导纳矩阵与特征阻抗矩阵的乘积的特征值与特征向量。对于高维的导纳矩阵与特征阻抗矩阵的乘积矩阵，尤其是对于有损导体和有耗介质的情形，两类矩阵均为复数矩阵，且与频率有关。因此，计算其特征值与特征的向量的计算量与内存开销是相当大的。从而使得求解由多导体传输线组成的电缆上的电压波或电流的计算量与内存开销变得很大。本文针对有损导体与无耗介质和有损导体与有耗介质的一般情形，采用文献 [7] 中迭代QR方法计算导纳矩阵和特征矩阵的乘积矩阵的特征值，再采用迭代算法计算特征向量，约简了求解多导体传输线方程的计算量与内存开销。最后给出了具体算例。

现在，求解MTL方程最常见的方法是QR算法。但传统的QR算法，仍然需要重复矩阵的数百万次甚至数千万次的乘法。因此，需要实现QR算法的并行化，以减少计算时间。本文根据文献 [8] 中介绍的一般方法，提出了一种并行的QR分解算法来求解MTL方程。我们还提供了并行算法和串行算法之间的时间的比较。

2. N线多导体传输线方程的导出

对于由N条均匀的平行细导体和一条参考导体组成的N-线多导体传输线，考虑导体是有损的，电介质也是有耗的.设导体平行于z轴，假设外加于第n条导体的激励电压源为 $v_n^{\left(s\right)}\left(z,\omega \right)$，激励电流源为 $i_n^{\left(s\right)}\left(z,\omega \right)$，则控制N-线多导体传输线上电压与电流传播的方程为

$\frac{\text{d}}{\text{d}z}{i}_n\left(z,\omega \right)+{\displaystyle {\sum }_{m=1}^N{y^{\prime }}_{nm}\left(\omega \right)v_m\left(z,\omega \right)}=i_n^{\left(s\right)}\left(z,\omega \right),n=1,2,3,\cdots ,N$ (1)

$\frac{\text{d}}{\text{d}z}{v}_n\left(z,\omega \right)+{\displaystyle {\sum }_{m=1}^N{z^{\prime }}_{nm}\left(\omega \right)i_m\left(z,\omega \right)}=v_n^{\left(s\right)}\left(z,\omega \right),n=1,2,3,\cdots ,N$ (2)

其中 ${y^{\prime }}_{nm}\left(z,\omega \right)$ 为对应于频率 $\omega$ 的第n条均匀导体相对于第m条均匀导体每单位长度上的导纳，与z无关， ${z^{\prime }}_{nm}\left(z,\omega \right)$ 为相应的特征阻抗。以向量 $I\left(z,\omega \right),V\left(z,\omega \right)$ 分别记N-线传输线上的电流向量与电压向量，以矩阵 $Y^{\prime }\left(\omega \right)=\left({y^{\prime }}_{nm}\left(\omega \right)\right),Z^{\prime }\left(\omega \right)=\left({z^{\prime }}_{nm}\left(\omega \right)\right)$ 分别记N-线传输线上导纳与特征阻抗，以向量 $I^{\left(s\right)}\left(z,\omega \right),V^{\left(s\right)}\left(z,\omega \right)$ 分别记外加激励源的电流与电压向量，则N-线多导体传输线方程(1)、(2)可表示为

$\frac{\text{d}}{\text{d}z}I\left(z,\omega \right)+Y^{\prime }\left(\omega \right)V\left(z,\omega \right)=I^{\left(s\right)}\left(z,\omega \right)$ (3)

$\frac{\text{d}}{\text{d}z}V\left(z,\omega \right)+Z^{\prime }\left(\omega \right)I\left(z,\omega \right)=V^{\left(s\right)}\left(z,\omega \right)$ (4)

方程(3)、(4)是带激励源的N-线多导体传输线方程的一般形式，其中激励源可分为天线模与传输线模，而因天线模在传输终端为零，一般只考虑传输线终端的响应，故常忽略天线模。这里考虑的是正弦型激励源。

在有损导体与有耗介质的情形下， $Y^{\prime }\left(\omega \right)$ 与 $Z^{\prime }\left(\omega \right)$ 均为复矩阵，为解方程(3)、(4)，希望去掉 $I\left(z,\omega \right)$ 与 $V\left(z,\omega \right)$ 之间的耦合。为此，用非奇异矩阵 $T\left(\omega \right)={\left(t_{nm}\right)}_{N\times N}$ 左乘方程(3)的两边，再与(4)的两边相加，得

$\begin{array}{l}\frac{\text{d}}{\text{d}z}\left[T\left(\omega \right)I\left(z,\omega \right)+V\left(z,\omega \right)\right]\\ =-\left[T\left(\omega \right)Y^{\prime }\left(\omega \right)V\left(z,\omega \right)+Z^{\prime }\left(\omega \right)I\left(z,\omega \right)\right]+\left[T\left(\omega \right)I^{\left(s\right)}\left(z,\omega \right)+V^{\left(s\right)}\left(z,\omega \right)\right]\end{array}$ (5)

令

$V_T\left(z,\omega \right)=T\left(\omega \right)I\left(z,\omega \right)+V\left(z,\omega \right)$ (6)

$V_T^{\left(s\right)}\left(z,\omega \right)=T\left(\omega \right)I^{\left(s\right)}\left(z,\omega \right)+V^{\left(s\right)}\left(z,\omega \right)$ (7)

则方程组(5)可表示为

$\frac{\text{d}}{\text{d}z}{V}_T\left(z,\omega \right)=-\left[T\left(\omega \right)Y^{\prime }\left(\omega \right)V\left(z,\omega \right)+Z^{\prime }\left(\omega \right)I\left(z,\omega \right)\right]+V_T^{\left(s\right)}\left(z,\omega \right)$ (8)

令

$T\left(\omega \right)Y^{\prime }\left(\omega \right)V\left(z,\omega \right)+Z^{\prime }\left(\omega \right)I\left(z,\omega \right)=B\left(\omega \right)V_T\left(z,\omega \right)$ (9)

则要求同时成立

$B\left(\omega \right)T\left(\omega \right)=Z^{\prime }\left(\omega \right),B\left(\omega \right)=T\left(\omega \right)Y^{\prime }\left(\omega \right)$ (10)

于是，由(10)的后一式，有

$T\left(\omega \right)=B\left(\omega \right){\left(Y^{\prime }\left(\omega \right)\right)}^{-1}$ (11)

代入(10)式的前一式，有

$B^2\left(\omega \right)=Y^{\prime }\left(\omega \right)Z^{\prime }(\; \omega \; )$

如果 $Y^{\prime }\left(\omega \right)Z^{\prime }\left(\omega \right)$ 能够对角化，即存在酉矩阵 $U\left(\omega \right)$，使得

$B^2\left(\omega \right)=U^{*}\left(\omega \right)Y^{\prime }\left(\omega \right)Z^{\prime }\left(\omega \right)U\left(\omega \right)=\text{diag}\left({\gamma }_1^2,{\gamma }_2^2,\cdots ,{\gamma }_N^2\right)$ (12)

取 ${\gamma }_k=q{\left({\gamma }^2\right)}^{1/2},k=1,2,\cdots ,N$，则

$Y^{\prime }\left(\omega \right)Z^{\prime }\left(\omega \right)=U\left(\omega \right)={\left(U\left(\omega \right)q\text{diag}\left({\gamma }_1,{\gamma }_2,\cdots ,{\gamma }_N\right)\right)}^{*}\left(U\left(\omega \right)q\text{diag}\left({\gamma }_1,{\gamma }_2,\cdots ,{\gamma }_N\right)\right),q=\pm 1$ (13)

从而可取

$B_q\left(\omega \right)=U\left(\omega \right)q\text{diag}\left({\gamma }_1,{\gamma }_2,\cdots ,{\gamma }_N\right),q=\pm 1$ (14)

由(10)的第二式知

$T_q\left(\omega \right)=U\left(\omega \right)q\text{diag}\left({\gamma }_1,{\gamma }_2,\cdots ,{\gamma }_N\right){\left[Y^{\prime }\left(\omega \right)\right]}^{-1},q=\pm 1$ (15)

于是方程(8)可表示为

$\frac{\text{d}}{\text{d}z}{V}_{T,q}\left(z,\omega \right)=-B_q\left(\omega \right)V_{T,q}\left(z,\omega \right)+V_{T,q}^{\left(s\right)}\left(z,\omega \right),q=\pm 1$ (16)

其中 $q=+1$ 对应着沿z轴正向的波， $q=-1$ 对应于沿z轴负向的波，而称 $V_{T,q}\left(z,\omega \right),q=\pm 1$ 为组合电压波。

从方程组(15)求得组合电压波 $V_{T,q}\left(z,\omega \right),q=\pm 1$ 后，则可从下两式求得 $I_q\left(z,\omega \right)$ 与 $V_q\left(z,\omega \right)$，

$I_q\left(z,\omega \right)=T_q^{-1}\left(\omega \right)\left(V_{T,q}\left(z,\omega \right)-V_q\left(z,\omega \right)\right)$ (17)

$V_q\left(z,\omega \right)=Z_q\left(\omega \right)I_q\left(z,\omega \right)$ (18)

其中

$Z_q\left(\omega \right)=B_q^{-1}\left(\omega \right)Z^{\prime }\left(\omega \right)$ (19)

文献 [1] 采用正实矩阵的特征展开方法讨论 $Y^{\prime }\left(\omega \right)Z^{\prime }\left(\omega \right)$ 的对角化问题和方程组(16)的解，但没有给出 $Y^{\prime }\left(\omega \right)Z^{\prime }\left(\omega \right)$ 的特征值与特征向量的具体计算方法。而且，对于无损导体与无耗介质以及有损导体与无耗介质的情形， $Y^{\prime }\left(\omega \right)Z^{\prime }\left(\omega \right)$ 的对角化的变换矩阵与频率 $\omega$ 无关，因此用特征模展开方法对角化 $Y^{\prime }\left(\omega \right)Z^{\prime }\left(\omega \right)$ 增加了计算量和内存开销。

因此，如果我们想解决这个问题，实现矩阵对角化是必要的。因此，我们的工作是将这个串行过程转换为并行算法。

3. QR算法

从图1中可以看出，QR算法可以分为两部分。

第一部分是建立Householder矩阵H，并进行正交变换，将一般矩阵A变为上Hessenberg矩阵B。具体步骤如下。

Figure 1. Flow chart for QR algorithm

图1. QR算法流程图

第二部分是利用给定的变换对上Hessenberg矩阵进行QR分解。具体步骤如图2所示。

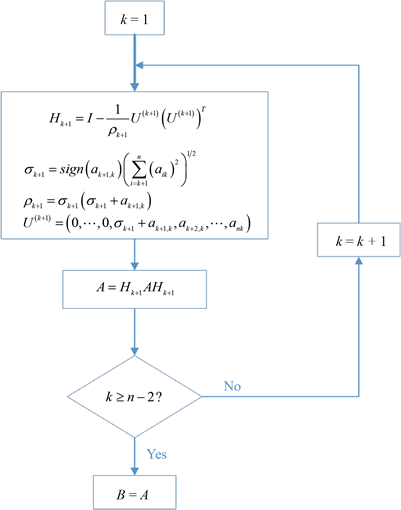
Figure 2. The steps of turning a general matrix into a upper Hessenberg matrix

图2. 将一般矩阵变换为上Hessenberg矩阵的步骤

按图2所示过程进行迭代，将得到主对角线矩阵的特征值的数值解。

4. QR算法的并行化

QR算法如图4所示。其中第二部分，是QR分解，是迭代的，很难解耦。因此，我们选择第一部分来实现其并行性。

在第一部分中，可以看到矩阵乘法消耗了大部分时间。因此，我们在CUDA中的矩阵乘法函数的基础上开发了一个并行算法。并行算法的过程如图3所示。

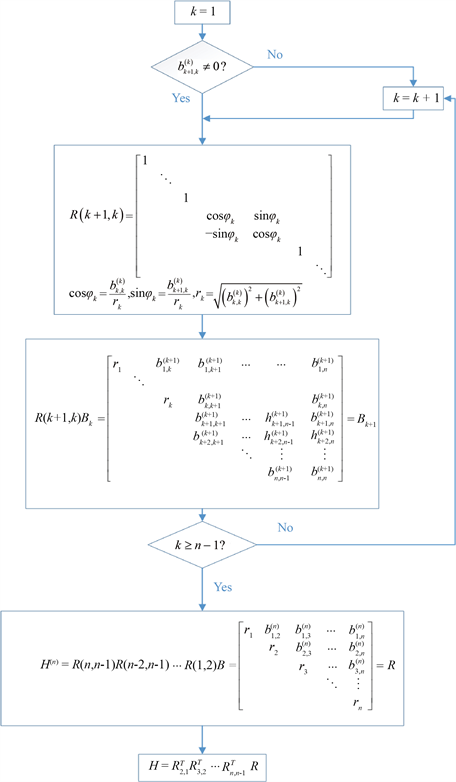
Figure 3. The steps of QR decomposition over the upper Hessenberg matrix

图3. 上Hessenberg矩阵上的QR分解步骤

Figure 4. Flow chart for QR algorithm

图4. QR算法的流程

首先，在GPU上申请一个内存块，然后将初始矩阵从CPU传递给GPU。从而，如图2所示，只需计算GPU的计算时间。在图4所示的每个计算周期中，我们构建了一个Household矩阵。由于矩阵乘法的并行化方法是很成熟的，可将每个乘法实现并行法。我们构建了一个并行算法来将一般矩阵转换为上Hessenberg矩阵。

从图5可以看出，对于小维问题，CUDA比C++慢。事实上，诸如OpenMP这样的并行实现并没有多大好处。然而，对于大规模的问题，并行实现显著加快了计算速度。CUDA是最快的实现，运行时间小于C++的10%。

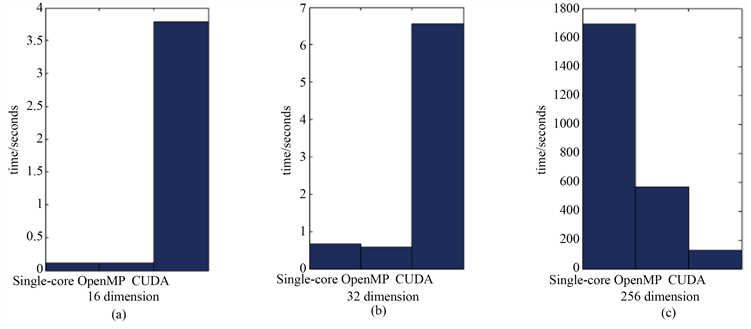
Figure 5. Comparison of three algorithms in three dimensions

图5. 三种算法的三维比较

5. 试验结果

我们在不同的平台上实现了该算法：C++语言中的串行算法，支持OpenMP的并行算法和CUDA上的并行算法。由于一根电缆通常由16或32或256根线组成，所以我们选择16阶、32阶和256阶矩阵来测试这些算法。结果如表1所示。

Table 1. Running time of different algorithms

表1. 不同算法的运行时间

从上述数据可以看出，对于大型矩阵，并行算法比串行算法具有很大的优势。当矩阵足够大时，CUDA可以节省更多的计算时间。然而，当矩阵的阶数不够高时，OpenMP会更好。

6. 结论

本文提出了一种基于CUDA的并行化方法，实现了QR算法来求解MTL方程。为了说明方法的有效性，实现了三种不同类型的算法：传统的单线程C++，使用OpenMP加速的C++和NvidiaCUDA。结果表明，当问题的维度达到数百个时，CUDA的GPU实现明显比单线程C++和OpenMP的CPU实现更有效。

基金项目

本研究由湖南省衡阳市科技创新平台计划(重点实验室)项目“大数据交通应急管理实验室”资助，批准号202010041588。

本研究由国家自然科学基金项目11271370资助。

参考文献

NOTES

^*通讯作者。