基于改进的近似l₀范数的稀疏信号重构算法

A Sparse Signal Reconstruction Algorithm Based on Improved Approximate l₀ Norm

摘要: 稀疏信号重构算法是压缩感知的关键。基于近似l₀范数的稀疏信号重构可以通过选取一个光滑函数近似l₀范数，从而将l₀范数最小化问题转化为光滑函数的优化问题。为了提高压缩感知中稀疏信号重构的精度，本文提出了一种基于改进的近似l₀范数的稀疏信号重构算法。该算法首先利用一种改进的光滑函数来近似l₀范数；其次利用外点罚函数法和共轭梯度法求解基于该光滑函数的优化问题的稀疏解；最后进行了多项实验来验证所提出算法的有效性。实验结果表明：相比于光滑l0算法、基追踪算法和非凸复合稀疏基算法，本文所提算法在重构误差、信噪比和恢复成功率等方面更具优越性。

Abstract: The sparse signal reconstruction algorithm is the key to compressive sensing. The sparse signal reconstruction based on approximate l₀ norm can be achieved by choosing a smooth function to approximate l₀ norm, thus the minimization problem of l₀ norm is transformed into an optimization problem of a smooth function. To improve the accuracy of the sparse signal reconstruction in compressive sensing, a sparse signal reconstruction algorithm based on an improved approximate l₀ norm is proposed in this paper. Firstly, a smooth function is proposed to approximate l₀ norm. Then, the sparse solution of this optimization problem that based on the smooth function is solved by exterior point penalty function method and conjugate gradient method. Finally, a number of experiments are carried out to verify the performance of the proposed algorithm. The experimental results show that the proposed algorithm is more superior in reconstruction error, signal-to-noise ratio and recovery success rate compared with smoothed l0 algorithm, the basis pursuit algorithm and the non-convex composite sparse bases algorithm.

1. 引言

传统的数据采集需要满足奈奎斯特采样定理，即为了不失真的恢复信号，采样频率必须大于信号最高带宽的两倍。但在这一理论指导下所获得的信息是冗余的，极大的影响了信息领域的发展。压缩感知(Compressive Sensing, CS) [1] 是一种新型的信号采集与重构理论，它可通过远低于奈奎斯特标准的方式进行数据采样，并仍能够精确地恢复稀疏信号。该理论提出后，在阵列信号处理 [2]、医学影像 [3] 和雷达探测 [4] 等领域受到高度关注，展现出了巨大的应用价值。压缩感知理论主要包括三部分：信号的稀疏表示、测量矩阵的设计和稀疏信号重构。其中，稀疏信号重构是指从较少的测量值中精确地恢复原始信号，是CS理论中最重要的一部分。信号的重构精度主要取决于重构算法的性能，设计高效的重构算法是提高稀疏信号重构精度的关键。因此，稀疏信号重构算法具有重要的研究意义。

从数学的角度来看，通常使用以下最小化方法对稀疏信号重构问题进行建模 [5]：

$\underset{x\in {\text{R}}^n}{\min }{\Vert x\Vert }_0\text{s}\text{.t}\text{.}Ax=b$ (1)

其中 $A\in {\text{R}}^{m\times n}\left(m<n\right)$ 是感知矩阵， $b\in {\text{R}}^m$ 是测量向量， $x\in {\text{R}}^n$ 是未知的稀疏向量， ${\Vert x\Vert }_0$ 是实向量x的零范数。

然而，由于l₀范数的不连续性，使得基于l₀范数的重构模型的直接求解是NP (Non-deterministic Polynomial)难的 [6]，其计算量会随稀疏向量维数的增加而增大，且模型的抗噪能力较差。为此学者们提出了很多方法对最小化l₀范数进行近似求解，如贪婪方法、凸松弛方法和非凸松弛方法等。贪婪算法通过选择与信号重构残差最匹配的原子进行信号重构，传统的贪婪算法有正交匹配追踪算法 [7]、广义正交匹配追踪算法 [8] 和子空间追踪算法 [9] 等，这类算法重构理论简单、计算速度较快，但重构精度较低，需要更多观测值。凸松弛方法将最小化l₀范数转化为最小化l₁范数，其中典型的算法有基追踪算法 [10]、迭代阈值算法 [11] 和梯度投影法 [12] 等，这类算法重构精度较高、所需测量值较少，但计算复杂度较高，不适合求解大规模问题。因此这两类算法应用范围有限。

近年来，利用非凸松弛方法近似求解l₀范数受到了广泛关注。常见的非凸松弛方法使用l_p范数、高斯类函数或分式类函数近似l₀范数，其中高斯类函数是一种最常见的近似函数。最早Mohimani等人提出了光滑l₀ (Smoothed l₀ norm, SL0)算法 [13]，该算法利用标准高斯函数近似l₀范数，并结合最速下降法寻求最优解；随后林婉娟等人提出了利用双曲正切函数和修正牛顿法的牛顿光滑l₀ (Newton Smoothed l₀ norm, NSL0)算法 [14]；张巍等人通过引入近似双曲正切函数和混合优化方法提出了近似阻尼牛顿光滑l₀ (Almost- Hybird Newton Smoothed l₀ norm, A-HNSL0)算法 [15]；2020年，周洁容等人提出的非凸复合稀疏基(Non-convex Composite Sparse bases, NCCS)算法 [16] 中采用复合指数函数近似l₀范数，并结合外点罚函数法和共轭梯度法求得最优解。这类方法对稀疏信号的恢复性能由所使用的函数对l₀范数的逼近程度以及对该函数的求解方法所决定。

SL0算法具有重构速度快，算法简单等优点，但该算法采用的高斯函数的陡峭性不大，不能更好地逼近l₀范数，且利用最速下降法进行求解会产生“锯齿现象”，不能求得全局最优解，从而导致算法重构精度不高。针对以上不足，本文利用一种陡峭性更强的非凸光滑函数逼近l₀范数，并通过外点罚函数法和共轭梯度法求得稀疏解，提出了一种改进的近似l₀范数的稀疏信号重构算法，即INCS (Improved non-convex sparse bases)算法。最后通过仿真实验验证了本文算法在重构误差、信噪比和恢复成功率等方面较于SL0算法、基追踪算法和NCCS算法的优越性。

2. SL0算法

压缩感知中稀疏信号重构算法是求解最优化问题(1)，对任意的 $x\in {\text{R}}^n$， ${\Vert x\Vert }_0$ 可表示为 ${\Vert x\Vert }_0={\displaystyle \underset{i=1}{\overset{n}{\sum }}\delta \left(x_i\right)}$，其中 $\delta \left(x_i\right)=\{\begin{array}{l}\text{0}{x}_i=0\\ 1x_i\ne 0\end{array}$。

由于l₀范数是不连续的，SL0算法中Mohimani等人首次提出利用连续函数 $f_{\sigma }\left(x_i\right)=1-{\text{e}}^{-\frac{x_i{}^2}{2{\sigma }^2}}$ 来逼近 $\delta \left(x_i\right)$，其中 $\sigma \left(0<\sigma <1\right)$ 为控制参数，显然有：

$\underset{\sigma \to 0}{\lim }{f}_{\sigma }\left(x_i\right)=\{\begin{array}{l}0x_i=0\\ 1x_i\ne 0\end{array}$ (2)

令 $F_{\sigma }\left(x\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{f}_{\sigma }\left(x_i\right)}$，对任意的 $x\in {\text{R}}^n$，可得到 $\underset{\sigma \to 0}{\lim }{F}_{\sigma }\left(x\right)={\Vert x\Vert }_0$。故最小化l₀范数问题(1)可转化为

以下优化问题：

$\underset{x}{\min }{F}_{\sigma }\left(x\right)\text{s}\text{.t}\text{.}Ax=b$ (3)

SL0算法利用最速下降法和梯度投影原理求解该优化问题。该算法具有重构速度快，算法简单等优点，但采用的连续函数的陡峭性不大，使得近似l₀范数的估计不准确；且最速下降法会出现“锯齿现象”，不能求得全局最优解，从而导致算法的重构精度不高。

3. 基于改进的近似l₀范数的稀疏信号重构算法

3.1. 改进的近似l₀范数

为了提高近似函数对l₀范数的逼近程度，本文采用一种改进的非凸光滑函数近似l₀范数：

$f_{\sigma }\left(x\right)=1-{\text{e}}^{-\frac{c\left|x\right|}{{\sigma }^2}}$ (4)

其中c为大于等于1的常数， $\sigma \left(0<\sigma <1\right)$ 为控制参数。

文献 [13] 和 [16] 中分别采用了以下两种函数来近似l₀范数：

$p_{\sigma }\left(x\right)=1-{\text{e}}^{-\frac{x^2}{2{\sigma }^2}}$ 、 $h_{\sigma }\left(x\right)=1-{\text{e}}^{-\frac{\left|x\right|}{\sigma \left(\left|x\right|+\sigma \right)}}$

下面从几何图像和理论分析上说明本文提出的函数 $f_{\sigma }\left(x\right)$ 比函数 $p_{\sigma }\left(x\right)$ 和 $h_{\sigma }\left(x\right)$ 更逼近l₀范数。

1) 几何图像分析

函数 $f_{\sigma }\left(x\right)$ 、 $p_{\sigma }\left(x\right)$ 和 $h_{\sigma }\left(x\right)$ 的几何图像如图1所示，可以看出，函数 $f_{\sigma }\left(x\right)$ 的图像曲线相比于其他两种函数更陡峭，即函数 $f_{\sigma }\left(x\right)$ 对l₀范数的逼近效果更好。

Figure 1. Comparison chart of the three functions at $\sigma =0.1,c=1$

图1. $\sigma =0.1,c=1$ 时三种函数的对比图

2) 理论分析

假定 $x\ge 0$，则对区间内任意 $\sigma \left(\sigma \ne 0\right)$ 有 $p_{\sigma }\left(x\right)=1-{\text{e}}^{-\frac{x^2}{2{\sigma }^2}}$ 、 $h_{\sigma }\left(x\right)=1-{\text{e}}^{-\frac{x}{\sigma \left(x+\sigma \right)}}$ 、 $f_{\sigma }\left(x\right)=1-{\text{e}}^{-\frac{cx}{{\sigma }^2}}$，

因为

$h_{\sigma }\left(x\right)-p_{\sigma }\left(x\right)={\text{e}}^{-\frac{x^2}{2{\sigma }^2}}-{\text{e}}^{-\frac{x}{\sigma \left(x+\sigma \right)}}$ (5)

所以比较函数 $p_{\sigma }\left(x\right)$ 和 $h_{\sigma }\left(x\right)$ 的大小只需要比较他们的指数大小，易得：

$-\frac{x^2}{2{\sigma }^2}-\left(-\frac{x}{\sigma \left(x+\sigma \right)}\right)=\frac{x}{\sigma }\left(\frac{1}{x+\sigma }-\frac{x}{2\sigma }\right)\ge 0$ (6)

因此 $h_{\sigma }\left(x\right)\ge p_{\sigma }\left(x\right)$ ；

同理

$f_{\sigma }\left(x\right)-h_{\sigma }\left(x\right)={\text{e}}^{-\frac{x}{\sigma \left(x+\sigma \right)}}-{\text{e}}^{-\frac{cx}{{\sigma }^2}}$ (7)

因为

$-\frac{x}{\sigma \left(x+\sigma \right)}-\left(-\frac{cx}{{\sigma }^2}\right)=\frac{x}{\sigma }\left(\frac{c}{\sigma }-\frac{1}{x+\sigma }\right)\ge 0$ (8)

所以 $f_{\sigma }\left(x\right)\ge h_{\sigma }\left(x\right)$。

利用函数对称性， $x<0$ 时也可类似讨论。因此可以得到 $p_{\sigma }\left(x\right)\le h_{\sigma }\left(x\right)\le f_{\sigma }\left(x\right)$，即当 $x\ne 0$ 时，函数 $f_{\sigma }\left(x\right)$ 对应的函数值比其他两种函数对应的函数值更加接近于1，这意味着函数 $f_{\sigma }\left(x\right)$ 比其他两种函数更逼近l₀范数。

3.2. 算法实现

下面基于所改进的函数 $f_{\sigma }\left(x\right)$ 对(3)式进行求解。令 $x=u-v$，其中 $u,v\in {\text{R}}^n$，u为x中所有的正元，其余元素为零；v为x中所有负元的绝对值，其余元素也为零，利用 $z={\left[u^{\text{T}},v^{\text{T}}\right]}^{\text{T}}\in {\text{R}}^{2n}$ 表示拼接向量。

经过替换，可得：

$F_{\sigma }\left(z\right)=F_{\sigma }\left(x\right)={\displaystyle \underset{i=1}{\overset{2n}{\sum }}\left(1-{\text{e}}^{-\frac{c{z}_i}{{\sigma }^2}}\right)}$ (9)

此时约束条件 $Ax=b$ 转化为 $\left[A,-A\right]z=b$，所以(3)式转化为：

$\underset{z}{\min }{F}_{\sigma }\left(z\right)\text{s}\text{.t}\text{.}\left[A,-A\right]z=b,z\ge 0$ (10)

为了方便求解(10)式，利用非凸函数 $F_{\sigma }\left(z\right)$ 的一阶判别条件及优化最小化(Majorize-Minorize, MM)方法 [17] 对目标函数 $F_{\sigma }\left(z\right)$ 进行放缩，可得：

$F_{\sigma }\left(z\right)\le F_{\sigma }\left(\tilde{z}\right)+\langle z-\tilde{z},\nabla F_{\sigma }\left(\tilde{z}\right)\rangle \le F_{\sigma }\left(\tilde{z}\right)+\langle z-\tilde{z},\nabla F_{\sigma }\left(\tilde{z}\right)\rangle +\lambda \left({\Vert z-\tilde{z}\Vert }_2{}^2+{\Vert z-\tilde{z}\Vert }_1\right)$ (11)

记

$H_{\sigma }\left(z,\tilde{z}\right)=F_{\sigma }\left(\tilde{z}\right)+\langle z-\tilde{z},\nabla F_{\sigma }\left(\tilde{z}\right)\rangle +\lambda \left({\Vert z-\tilde{z}\Vert }_2{}^2+{\Vert z-\tilde{z}\Vert }_1\right)$ (12)

其中 $z,\tilde{z}$ 为可行域中的点， $\lambda \left(\lambda >1/{\sigma }^2\right)$ 为常值，则 $H_{\sigma }\left(z,\tilde{z}\right)$ 为 $F_{\sigma }\left(z\right)$ 的一个上界函数。

忽略常值后，则(10)式的解由下式迭代求得：

$z_{k+1}^{\sigma }=\underset{z}{\arg \min }\{\langle \nabla F_{\sigma }\left(z_k^{\sigma }\right),z\rangle +\lambda \left({\Vert z-z_k^{\sigma }\Vert }_2{}^2+{\Vert z-z_k^{\sigma }\Vert }_1\right)|\left[A,-A\right]z=b,z\ge 0\}$ (13)

其中 $z_k^{\sigma }\left(k=1,2,3,\cdots \right)$ 为可行域中的点，取值与 $\sigma$ 有关。

令

$\{\begin{array}{l}\langle \nabla F_{\sigma }\left({\tilde{z}}^{\sigma }\right),z\rangle +\lambda \left({\Vert z-\tilde{z}\Vert }_2^2+{\Vert z-\tilde{z}\Vert }_1\right)=G\left(z\right)\\ \left[A,-A\right]z-b=H\left(z\right)={\left(h_1\left(z\right),\cdots ,h_m\left(z\right)\right)}^{\text{T}}\\ z=W\left(z\right)={\left(w_1\left(z\right),\cdots ,w_{2n}\left(z\right)\right)}^{\text{T}}\end{array}$

则(13)可简记为：

$\underset{z}{\min }G\left(z\right)\text{s}\text{.t}\text{.}H\left(z\right)=0,W\left(z\right)\ge 0$ (14)

因此，(3)式的优化问题转化为(14)式的优化问题。

本文利用外点罚函数法 [18] 和共轭梯度法迭代求解(14)式，具体步骤如下：

利用外点罚函数法引入正数M，本文取 $M=1$，放大倍数为5，将(14)式转化为以下无约束问题：

$z_{k+1}^{\sigma }=\underset{z}{\arg \min }{L}_{z_k^{\sigma }}\left(z,M\right)$ (15)

其中

$L_{z_k^{\sigma }}\left(z,M\right)=\langle \nabla F_{\sigma }\left(z_k^{\sigma }\right),z\rangle +\lambda \left({\Vert z-z_k^{\sigma }\Vert }_2^2+{\Vert z-z_k^{\sigma }\Vert }_1\right)+M\left(I^{\text{T}}\cdot U\left(z\right)+I^{\text{T}}\cdot H\left(z\right)\right)$ (16)

式中I为 $2n\times 1$ 的单位向量， $U\left(z\right)\text{=}{\left(\min \left(0,z_1^2\right),\cdots ,\min \left(0,z_{2n}^2\right)\right)}^{\text{T}}$， $H\left(z\right)=diag\left(\left[A,-A\right]z-b\right)\cdot \left(\left[A,-A\right]z-b\right)$，则函数 $L_{z_k^{\sigma }}\left(z,M\right)$ 有关z的一阶、二阶次梯度 [19] 分别为：

$\nabla L_{z_k^{\sigma }}\left(z,M\right)=\nabla F_{\sigma }\left(z_k^{\sigma }\right)+\lambda \left(2\left(z-z_k^{\sigma }\right)+\mathrm{sgn}\left(z-z_k^{\sigma }\right)\right)+2M\left\{V\left(z\right)+{\left[A,-A\right]}^{\text{T}}\cdot \left(\left[A,-A\right]z-b\right)\right\}$ (17)

${\nabla }^2{L}_{z_k^{\sigma }}\left(z,M\right)=2\lambda I+2M\cdot {\left[A,-A\right]}^{\text{T}}\left[A,-A\right]I$ (18)

其中 $V\left(z\right)={\left(\min \left(0,z_1\right),\cdots ,\min \left(0,z_{2n}\right)\right)}^{\text{T}}$。

再利用共轭梯度法迭代求解(15)式的 $z_{k+1}^{\sigma }$，其迭代更新格式为：

$z_{t+1}=z_t+{\alpha }_t\cdot p_t$ (19)

其中步长因子为：

${\alpha }_t=\frac{{\Vert \nabla L_{z_k^{\sigma }}\left(z_t,M\right)\Vert }_2^2}{p_t^{\text{T}}\cdot {\nabla }^2{L}_{z_k^{\sigma }}\left(z_t,M\right)\cdot p_t}$ (20)

下降方向为：

$p_t=-\nabla L_{z_k^{\sigma }}\left(z_t,M\right)+p_{t-1}\cdot {\rho }_{t-1}$ (21)

其中令 $z_k^{\sigma }=z_0$， $p_0=-\nabla L_{z_k^{\sigma }}\left(z_0,M\right)$， ${\rho }_{t-1}=\frac{{\Vert \nabla L_{z_k^{\sigma }}\left(z_t,M\right)\Vert }_2^2}{{\Vert \nabla L_{z_k^{\sigma }}\left(z_{t-1},M\right)\Vert }_2^2}$。

综上所述，本文所提出的INCS算法的流程如下：

Step 1输入：矩阵A、测量向量b， ${\epsilon }_1,{\epsilon }_2,{\epsilon }_3>0$ ；

Step 2初始化：

1) 设置递减序列 $\sigma$， ${\sigma }_{k+1}=\beta {\sigma }_k$，其中 $0<\beta <1$， $\beta$ 为 $\sigma$ 的递减因子，本文设置 $\beta =0.5$， ${\sigma }_0=2\max \left(\left|x_0\right|\right)$ ；

2) 设置初始值： $x_0=\underset{x}{\arg \min }\left\{{\Vert x\Vert }_1|Ax=b\right\}$， $z_0={\left[{\left(x_0^{+}\right)}^{\text{T}},{\left(x_0^{-}\right)}^{\text{T}}\right]}^{\text{T}}$ ；

Step 3算法迭代：

1) $k=0$， $\sigma ={\sigma }_0$ ；

2) while $d_1>{\epsilon }_1$ do

1：{ ${\hat{z}}_0=z_k$, $l=0$, $k=k+1$，

2：while $d_2>{\epsilon }_2$ do

3：{ $l=l+1$，

4： ${\hat{z}}_l=\underset{z}{\arg \min }\left\{G_{l-1}\left(z\right)|\left[A,-A\right]z=b,z\ge 0\right\}$，

5： $d_2=\frac{{\Vert {\hat{z}}_l-{\hat{z}}_{l-1}\Vert }_2}{{\Vert {\hat{z}}_{l-1}\Vert }_2}$ }

6： $z_k={\hat{z}}_l$，

7： $d_1=\frac{{\Vert {\hat{z}}_k-{\hat{z}}_{k-1}\Vert }_2}{{\Vert {\hat{z}}_{k-1}\Vert }_2}$，

8： $\sigma =\beta \sigma$ }，

9： $x_k=z_k\left(1:n\right)-z_k\left(n+1:end\right)$，

10： $W=\frac{1}{\left|x_{k-1}\right|+{\epsilon }_3}$，

11： $x_k=\underset{x}{\arg \min }\left\{{\Vert Wx\Vert }_1|Ax=b\right\}$ ；

Step 4输出稀疏向量： $x=x_k$。

其中Step 3由内、外两部分循环构成。外循环由步骤1~2及6~8组成，通过参数 $\sigma$ 实现函数 $f_{\sigma }\left(x\right)$ 对 $l_0$ 范数的逐次逼近；内循环为步骤3~5，利用外点罚函数法和共轭梯度法迭代求解步骤4；并将求得的解利用加权 $l_1$ 范数最小化 [20] 进行稀疏化处理。 $d_1$ 和 $d_2$ 分别表示外、内循环连续迭代的解之间的相对误差，并用于判断循环是否停止。

4. 仿真实验与结果分析

为验证本文所提出的INCS算法在重构性能上的优越性，本节设计了几组有关SL0算法、基追踪(Basis Pursuit, BP)算法、NCCS算法和INCS算法的对比实验。对于每个实验，我们重复进行100次测试，给出平均结果，并取 $c=10$。仿真实验结果是在MatlabR2014a的条件下获得的。

在仿真实验中，矩阵A的大小为 $128\times 256$，其中矩阵元素服从零均值、单位方差的高斯分布，矩阵的列具有单位l₂范数；稀疏原信号x的维数为256，非零项服从正态分布；信号稀疏度k取值区间为 $\left[10,80\right]$。

实验中所涉及到的性能指标包括：

1) 重构误差(mean squared error)：

$MSE={\Vert \tilde{x}-\hat{x}\Vert }_2{}^2$

2) 信噪比(signal noise ratio)：

$SNR=10\cdot {\log }_{10}\left(\frac{{\Vert \tilde{x}\Vert }_2^2}{{\Vert \tilde{x}-\hat{x}\Vert }_2^2}\right)$

3) 算法运行时间

4) 恢复成功率(recovery success rate)：当 ${\tilde{x}}_i\ne 0$ 时， $\left|\tilde{x}-\hat{x}\right|\le {10}^{-4}$ 说明算法在该点处重构成功，

$RSS=\frac{\hat{x}重构成功的点个数}{\tilde{x}中非零点个数}$

其中 $\tilde{x}$ 表示稀疏原信号， $\hat{x}$ 表示算法的恢复信号；

图2为各算法的重构误差MSE和稀疏度的变化关系，实验结果如图2及表1所示。由图2和表1可见，BP算法、NCCS算法和INCS算法都存在随着稀疏度的增加重构误差增大的趋势。在同一稀疏度下，相比于其他三种算法，INCS算法的重构误差略小。

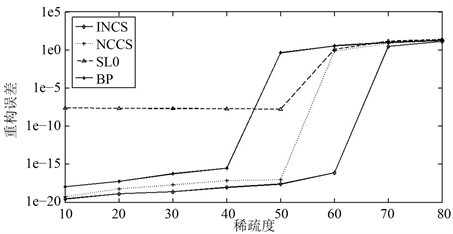
Figure 2. The relationship between the reconstruction error and sparsity of the SL0 algorithm, BP algorithm, NCCS algorithm and INCS algorithm

图2. SL0算法、BP算法、NCCS算法、INCS算法的重构误差和稀疏度的变化关系

Table 1. The numerical record of the reconstruction error of each algorithm changing with the sparsity k

表1. 各算法的重构误差随着稀疏度k变化的数值记录

图3为各算法的重构信噪比SNR和稀疏度的变化关系，实验结果如图3及表2所示。可以看出，在稀疏度区间 $\left[10,50\right]$ 上，INCS算法和NCCS算法的信噪比变化不大且相差很小，但明显高于SL0算法和BP算法的信噪比；在稀疏度区间 $\left[50,80\right]$ 上，各算法的信噪比随着稀疏度的增加而减小，但INCS算法的信噪比仍高于其他三种算法。

Figure 3. The relationship between the signal-to-noise ratio and sparsity of the SL0 algorithm, BP algorithm, NCCS algorithm and INCS algorithm

图3. SL0算法、BP算法、NCCS算法、INCS算法的重构信噪比和稀疏度的变化关系

Table 2. The numerical record of the signal-to-noise ratio of each algorithm changing with the sparsity k

表2. 各算法的重构信噪比随着稀疏度k变化的数值记录

图4为各算法的运行时间和稀疏度的变化关系，实验结果如图4及表3所示。可以看出，SL0算法和BP算法的运行时间较短并能够保持在0.5秒以内。在稀疏度区间 $\left[10,50\right]$ 上，INCS算法和NCCS算法的运行时间能保持在1秒以内，在稀疏度区间 $\left[50,80\right]$ 上这两种算法的运行时间都有所增加，但对比NCCS算法，INCS算法的运行时间始终略短。

Figure 4. The relationship between the running time and sparsity of the SL0 algorithm, BP algorithm, NCCS algorithm and INCS algorithm

图4. SL0算法、BP算法、NCCS算法、INCS算法的运行时间和稀疏度的变化关系

Table 3. The numerical record of the running time of each algorithm changing with the sparsity k

表3. 各算法的运行时间随着稀疏度k变化的数值记录

图5为各算法的恢复成功率RSS和稀疏度的变化关系，实验结果如图5及表4所示。可以看出，当稀疏度增加到一定程度时这四种算法的恢复成功率均开始降低。INCS算法的恢复成功率在稀疏度区间 $\left[10,60\right]$ 上都能保持为1，也就是说在这个区间内该算法都能够实现信号的完全恢复。在稀疏度区间 $\left[60,80\right]$ 上，INCS算法的恢复成功率始终略高于其他三种算法，所以利用INCS算法恢复信号时精确度有一定的提高。

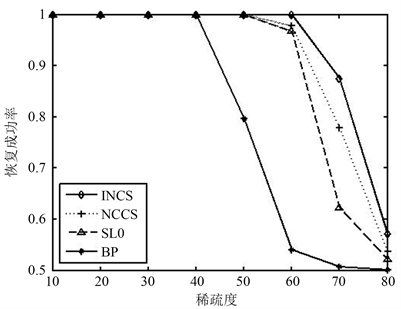
Figure 5. The relationship between the recovery success rate and sparsity of the SL0 algorithm, BP algorithm, NCCS algorithm and INCS algorithm

图5. SL0算法、BP算法、NCCS算法、INCS算法的恢复成功率和稀疏度的变化关系

Table 4. The numerical record of the recovery success rate of each algorithm changing with the sparsity k

表4. 各算法的恢复成功率随着稀疏度k变化的数值记录

综上所述，本文提出的INCS算法的综合重构性能优于实验中的对比算法，说明利用该算法能够更好的恢复稀疏信号。

5. 结论

本文提出了一种基于改进的近似l₀范数的稀疏信号重构算法，即INCS算法。该算法利用一种逼近性能更优的非凸光滑函数实现对l₀范数的逼近，并通过外点罚函数法和共轭梯度法求解基于该函数的稀疏解。实验结果表明：对比SL0算法、BP算法和NCCS算法，INCS算法在重构误差、信噪比和恢复成功率等方面表现出更优越的重构性能。

基金项目

长安大学中央高校基本科研业务费专项资金资助项目(编号：310812163504)。

参考文献

NOTES

^*通讯作者。