管壳式冷却器两相流动传热及压降特性分析

Analysis of Heat Transfer and Pressure Drop Characteristics of Two-Phase Flow in Shell-and-Tube Cooler

摘要: 本文针对某压缩机出口管壳式冷却器进行研究，通过理论分析并考虑其壳程热流体的相变影响，给出了壳程出口温度及压降的计算表达式，数值结果与已有实测数据进行了对比验证，研究了结构参数对其壳程出口温度及压降的影响。计算结果表明冷却器壳程出口温度随管程介质密度的增加而增加，同时随换热管的外径增大而减小。换热管和折流板的间距及其缺口高度对壳程的流阻压降影响显著，壳程压降随换热管横向及纵向管间距、折流板间距及缺口高度的增大而减小，随壳程流体流量的增大而增大，呈非线性变化。

Abstract: A shell-and-tube cooler at the outlet of a compressor is studied in this paper. Through theoretical analysis and considering the effect of phase change of the thermal fluid in the shell side, the calcu-lation expressions for the outlet temperature and pressure drop of the shell side are given. The numerical results are compared and verified with the existing measured data, and the influence of structural parameters on the outlet temperature and pressure drop of the shell side is studied. The calculation results show that the outlet temperature of the shell side of the cooler increases with the increase of the medium density of the tube side, and at the same time, it decreases with the increase of the outer diameter of the heat exchange tube. The heat exchange tube, the baffle spacing and the height of baffle notch have a significant effect on the pressure drop of the shell side. The pressure drop in the shell side decreases with the increase of the heat exchange tube’s transverse and longitudinal tube spacing, baffle spacing and notch height, and increases with the increase of the shell side fluid flow, showing a non-linear change.

1. 引言

热交换器工业企业中占有很重要的地位 [1]。由于管壳式冷却器结构简单、应用普遍、生产成本低、适用性强、处理量大，因而多应用于热交换换热设备中 [2]。而对于管壳式冷却器壳侧两相传热特性及压降的研究，可以完善冷却器传热过程分析以及流阻压降特性，对于提高冷却器换热效率以及在节约能源、提供换热效率方面具有重要意义 [3] [4]。

近年国内外许多学者对冷却器两相流进行了研究，黄国权等 [5] 针对壳侧流体介质为高温饱和蒸汽情况下，对不同介质入口速度和温度情况下冷却器壳侧传热系数、湍流动能和压降变化的模拟结果进行了比较，从而得出流体介质入口速度和温度对冷却器壳侧传热特点和传热性能的影响规律。文献 [6] [7] [8] [9] 建立了管壳式水冷冷凝器的换热模型基于该模型编制了管壳式冷凝器的仿真程序，并对冷凝器的性能进行模拟，对仿真结果进行了分析。Yang [10] 研究了垂直螺旋折流板管壳式冷却器壳体内丙烷的传热特性，得到了垂直螺旋板管壳式冷却器壳侧的流型和传热系数，并与实验数据进行了对比分析。

冷却器在工作过程中某些特定温度下会发生相变，从而导致冷却器的换热特性及压降分析十分复杂 [4] [11]。本文给出了某压缩机出口管壳式冷却器温度及压降理论计算的具体表达式，考虑了冷却器壳程热流体在传热过程中发生的相变影响，应用MATLAB软件编程计算壳程出口温度及压降值并与已有实验结果进行了对比验证，进一步研究了各参数对其结果的影响。

2. 几何模型及其数学描述

2.1. 几何模型

某供抽气机组压缩机出口使用管壳式冷却器，该冷却器外结构如图1所示。冷却器总长为5.840 m，管程入口及出口在冷却器端部圆面分布，壳程入口及出口分布于冷却器上部。冷却器由两个支架支撑固定。冷却器管束部分排列结构示意图如图2所示，具体为横排32根、竖排42根、41根交替排列。其中，管外径为18 mm，长度为5000 mm，数量1328根，管束排列为等边三角形排列形式。为改善换热效果，壳程使用折流板改变介质流向，且同时起到支承管束的作用，该冷却器内部有三个折流板,其形状为单弓形。冷却器内部局部结构三维示意图如图3所示，其相应的几何参数如表1所示。

Figure 1. Outline structure diagram of the shell-and-tube cooler

图1. 管壳式冷却器外形结构图

Figure 2. Tube bundle layout diagram

图2. 管束排列方式示意图

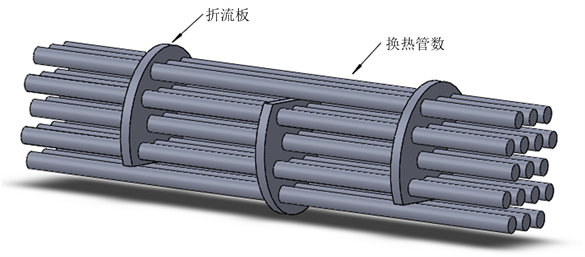
Figure 3. 3D schematic diagram of internal local structure

图3. 内部局部结构三维示意图

Table 1. Structural geometric parameters of the shell-and-tube cooler

表1. 管壳式冷却器结构几何参数

2.2. 数学模型

2.2.1. 传热过程

传热方程可由下述方程给出：

$Q_H=kA\Delta t_m$ (1)

$Q_H=q_{m1}{c}_1\left(t_h^1-t_h^2\right)=q_{m2}{c}_2\left(t_c^2-t_c^1\right)$ (2)

其中，Q_H为换热量，W；k为整个传热面上的平均传热系数，W∙(m²∙℃)⁻¹；A为传热面积，m²；Δt_m为两种流体间的平均温差℃。c₁和c₂分别为热流体、冷流体的定压比热容，kg∙(kg∙℃)；q_m1和q_m2分别为热流体及冷流体的质量流速，kg∙s； $t_h^1$ 和 $t_h^2$ 为热流体进出口温度， $t_c^1$ 和 $t_c^2$ 为冷流体进出口温度，单位均为℃。

冷却器性能通过有效度及热容量比测量，有效度ε_H由。方程给出：

${\epsilon }_H=\frac{q_H}{q_{H\max }}$ (3)

其中，q_H为冷却器的实际换热量，q_Hmax为冷却器的最大可能换热量，单位为W。热容量比C^*由下式给出：

$C^{\ast }=\frac{C_{\min }}{C_{\max }}=\{\begin{array}{l}\frac{t_c^2-t_c^1}{t_h^2-t_h^1},C_h=C_{\min }\\ \frac{t_h^1-t_h^2}{t_c^1-t_c^2},C_c=C_{\min }\end{array}$ (4)

式中，C_max为较大换热量；C_min为较小换热量；C_h为热流体热容量；C_c为冷流体热容量，单位均为W/℃。

若冷却器的总传热面积为F₁，总传热系数为K₁；壳程进口温度t_kin，壳程出口温度t_kout，壳程流量M_k，比热c_pk，热容量C_k = M_kc_pk；管程流体进口温度为t_gin，管程出口温度为t_gout，流量M_g，比热c_pg，热容量C_g = M_gc_pg。已知传热面积、传热系数及热容量，可求出传热单元数NTU：

$NTU=\frac{K_1\cdot F_1}{C_{\min }}$ (5)

其中

$C_{\min }=\{\begin{array}{l}{C}_k,C_k<C_g\\ C_g,C_g<C_k\end{array}$ (6)

壳程出口温度表达式为：

$\begin{array}{l}若C_{\min }=C_k,t_{kout}=t_{kin}-{\epsilon }_{{}_H}\left(t_{kin}-t_{gin}\right);\\ 若C_{\min }=C_g,t_{gout}=t_{gin}+{\epsilon }_H\left(t_{kin}-t_{gin}\right),t_{kout}=t_{kin}-Q_H/C_k;\end{array}$ (7)

由于壳程流体存在部分冷凝现象，水平管外冷凝时的表面换热系数为：

$\begin{array}{l}{\alpha }_1=0.725n_m{B}_m{r}_s^{\frac{1}{4}}\Delta t_0^{-\frac{1}{4}}{d}_0^{-\frac{1}{4}}\\ B_m=\left(9.81\rho {\lambda }^3\right)/{\nu }_m^{\frac{1}{4}}\end{array}$ (8)

式中，n_m为管束上冷凝时传热系数的修正系数；B_m为管壁上冷凝液膜的组合物性参数；r_s为潜热，J/kg；Δt₀为壳侧流体温度与管外污垢层外表面温度间的对数平均温差，℃；d₀为管外径，m；ρ为冷凝液膜的密度，kg/m³；λ为冷凝液膜的导热系数，W/(m∙K)⁻¹；v_m为冷凝液膜的运动粘，m²/s。

发生冷凝现象时，通常纯净的冷凝液体到壁面之间的换热量为

${Q^{\prime }}_H=h_{con}A\left(T_{sat}-T_w\right)$ (9)

式子中，h_con为冷凝时的换热系数，T_sat为冷凝液体在给定压力时所对应的饱和温度，T_w是壁面温度。

由于管程流体未发生冷凝现象，首先计算得到管程流体出口温度，从而得到管程流体的换热量，通过管程换热量及管外冷凝时的表面换热系数，并对其出口温度计算公式进行修正，从而得出适用于该冷却器的壳程出口温度数学公式：

${t^{″}}_{kout}=t_{\text{kin}}-{Q^{\prime }}_h/q_{m1}{c}_1$ (10)

2.2.2. 压降分析

管壳式冷却器壳程压降分为三部分，即中心区(交叉流区)压降；缺口压降；壳侧的入口和出口处的压降。中心区(交叉流区)压降可表示为：

$\Delta P_{b,id}=\frac{4f_{id}{G}_c^2}{2g_c{\rho }_s}{N}_{r,cc}{\left(\frac{{\mu }_w}{{\mu }_m}\right)}^{0.25}$ (11)

其中，N_r,cc为流过截面的有效管排数；G_c为交叉流区质量流量；f_id为单位管道的理想范宁摩擦因子；g_c是牛顿第二定律中的比例常数；μ_w是管壁处液体的粘性，μ_m是平均温度下液体的粘性；ρ_s为流体密度。

缺口压降与雷诺数有关：

$\Delta P_{w,id}=\{\begin{array}{l}\left(2+0.6N_{r,cw}\right)\frac{G_w^2}{2g_c{\rho }_s},Re\ge 100\\ \frac{26G_w{\mu }_s}{g_c{\rho }_s}\left(\frac{N_{r,cw}}{P_t-d_0}+\frac{L_b}{D_{h,w}^2}\right)+\frac{G_w^2}{g_c{\rho }_s},Re<100\end{array}$ (12)

其中，p_t为管距，N_r,cw为缺口内交叉流过管排的有效管数，L_b为折流板间距，D_h,w为缺口处水力直径。

壳侧的入口和出口区压降可表示为：

$\Delta P_{i-o}=2\Delta P_{b,id}\left(1+\frac{N_{r,cw}}{N_{r,cc}}\right){\xi }_b{\xi }_s$ (13)

冷却器的壳程压降表示为：

$\begin{array}{c}\Delta P_s=\Delta P_{cr}+\Delta P_w+\Delta P_{i-o}\\ =\left[\left(N_b-1\right)\Delta P_{b,id}{\xi }_b+N_b\Delta P_{w,id}\right]{\xi }_l+2\Delta P_{b,id}\left(1+\frac{N_{r,cw}}{N_{r,cc}}\right){\xi }_b{\xi }_s\end{array}$ (14)

其中N_b为折流板数；ξ_b为旁流压降修正因子；ξ_l为折流板与壳侧及管与折流板侧的泄露修正因子；ξ_s为进出口折流板截面不均匀流板间距产生的压降修正因子。

2.3. 理论计算具体表达式

基于上述冷却器温度及其压降理论公式，应用所研究冷却器的几何参数及相应的物料参数，可计算得到冷却器壳程出口的温度与压力，并与已有该冷却器的实际工况测量数据进行了对比验证。

在实际工况中，根据冷却器的进出口温度实测数据，发现温度存在较大差异，存在冷凝现象。因此，计算中由入口边界条件得到管程出口温度及总换热量，并通过实际工况中的参数推导出管外冷凝时的表面传热系数α，如下式

$\alpha =\frac{1863.9\times {\left(0.5980+1.373\times {10}^{-3}-5.333\times {10}^{-6}{P}_{kin}^2\right)}^3}{{\left(1.006{\epsilon }_H\left(t_{kin}-t_{kout}\right)\right)}^{0.25}\times {10}^{\left(\frac{230.298}{P_{kin}+126.203}-4.5668\right)}}$ (15)

冷却器的壳程出口温度t_kout：

$t_{kout}=0.13\left(t_{kin}-\frac{1.006C_k{\epsilon }_H\left(t_{kin}-t_{gin}\right)}{2460.7\alpha }\right)$ (16)

上式中，P_kin为壳程入口压力；t_kin为壳程入口温度，t_gin为管程入口温度；C_k为壳程热流体比热容，ε_H为冷却器有效度。C_k可表示为：

$C_k=\frac{2400W_y{A}_k}{4018\left(t_{yin}+273.15\right)\times \left({\left(P_{kin}/P_{yin}\right)}^{\frac{1}{4}}-1\right)}$ (17)

其中W_y为压缩机的功率，A_k为关于壳程入口温度及压力的多项式，表示为：

$A_k=1004.18+0.0171P_{kin}+\left(0.260175+0.000057142P_{kin}\right)t_{kin}+0.364286\times {10}^{-3}{t}_{kin}^2$ (18)

ε_H可表示为：

${\epsilon }_H=\frac{2}{\left(1+C^{*}\right)+\sqrt{1+C^{*}{}^2}\left(1+{\text{e}}^{-\frac{2460.7k}{C_k}\times \sqrt{\left(1+C^{*}{}^2\right)}}\right)/\left(1-{\text{e}}^{-\frac{2460.7k}{C_k}\times \sqrt{1+C^{*}{}^2}}\right)}$ (19)

其中传热系数k及热容量比C^*可分别表示为：

$C^{*}=C_k/\left(4.005P_{gin}^{0.8}\times \left(4184.4-0.6964t_{gin}+1.036\times {10}^{-2}{t}_{gin}^2\right)\right)$ (20)

$k=\frac{1}{4.56\times {10}^{-4}+1.281\times {10}^{-8}{\left(t_{kin}+273\right)}^{0.823}}$ (21)

P_gin为管程入口压力。

壳程出口压降通过推导计算获得，带入相关参数，化简后的出口压降ΔP_s为：

$\Delta P_s=\frac{167.134}{307.46A_t^{0.476}+22473.997A_t^{0.996}}+\frac{0.444}{A_{k2}}$ (22)

其中A_t为壳程入口温度的函数，A_k2为壳程入口温度及压力的函数：

$A_t=\frac{t_{kin}+273}{t_{kin}+395}$ (23)

$A_{k2}=\frac{P_{kin}}{273.15+t_{kin}}$ (24)

3. 计算结果与分析

基于以上管壳式冷却器的数学模型，应用MATLAB软件建立了管壳式冷却器进出口温度及压降计算仿真程序，其流程图如图4所示。

Figure 4. Program flow chart

图4. 程序流程图

3.1. 计算结果与实验结果的对比分析

给定冷却器结构参数，流体物性参数，其管程及壳程进口温度和压力采用已有实测数据，可计算得到壳程出口温度及压降，并与已有实验结果进行对比分析。图5为实验测得的壳程进口温度随时间变化曲线，利用该温度作为冷却器入口的初始条件，图6给出了考虑冷凝和不考虑冷凝壳程出口温度理论计算结果与已有实测值的对比曲线。可以看出壳程出口温度变化趋势与入口温度变化趋势一致，均随时间增加逐渐增大。考虑冷凝现象的计算结果较不考虑冷凝的结果更接近与实测值。由于冷却器壳程空气流动情况比较复杂，存在热对流等现象，本文计算中仅热传导，两者仍存在微小差异。

图7给出了该冷却器壳程进口压力实测曲线，图8给出了壳程出口压力计算结果与已有实测值的对比曲线，可以看出两者具有很好的一致性。图9给出了壳程压降随时间变化曲线，可以看出压降的变化与压力有关，压降随进口压力的增大而增大。壳程进出口温度及压力的计算值和实测结果为33,848个数据点，表2列出了其部分时间段的具体数值。

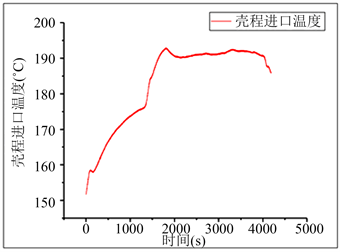
Figure 5. Shell side inlet temperature curve

图5. 壳程进口温度变化曲线

Figure 6. Shell side outlet temperature curve

图6. 壳程出口温度变化曲线

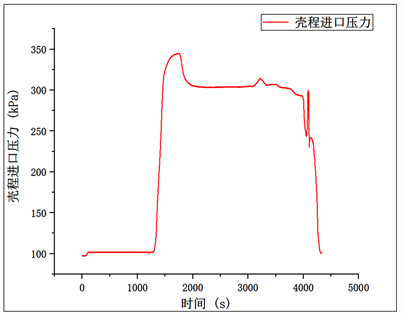
Figure 7. Shell side inlet pressure curve

图7. 壳程进口压力变化曲线

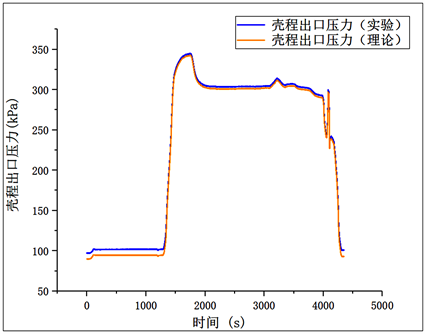
Figure 8. Shell side outlet pressure curve

图8. 壳程出口压力变化曲线

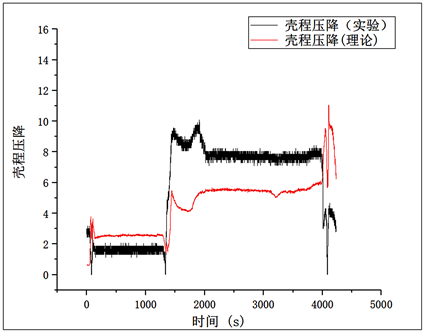
Figure 9. Shell side pressure drop curve

图9. 壳程压降变化曲线

Table 2. Partial calculation results and measured data of the shell-and-tube cooler

表2. 冷却器部分计算结果与实测数据

3.2. 各参数对冷却器性能的影响分析

3.2.1. 各参数对壳程出口温度的影响

由于冷却器性能参数对壳程出口温度及压降影响较大，为定量分析该影响作用，利用控制变量法分析壳程出口温度及压降随各参数的变化规律。图10给出了冷却器壳程出口温度随管程介质密度的变化曲线，可以看出其壳程出口温度随冷却器管程介质密度的增加而增加，呈非线性变化。图11给出了换热管外径对壳程出口温度的影响曲线，可以看出冷却器换热管的结构参数换热管外径同样影响着冷却器的换热特性和换热系数，冷却器壳程出口温度随换热管的外径增大而减小。

Figure 10. Effect of tube medium density on shell side outlet temperature

图10. 管程介质密度对壳程出口温度的影响

Figure 11. Effect of outer diameter of heat exchanger tube on outlet temperature of shell side

图11. 换热管外径对壳程出口温度的影响

3.2.2. 各参数对壳程压降的影响

冷却器中各重要的部件包括换热管、折流板的结构参数以及其布置方式均对冷却器流阻压降有显著的影响。图12和图13分别给出了换热管横向及纵向间距对壳程流阻压降的影响，可以看出随着换热管间距的增大，壳程的流阻压降逐渐减小，横向间距较纵向间距对其影响更为显著。图14和图15分别给出了折流板间距以及其缺口高度对壳程流阻压降的影响，增大折流板间距或者折流板的缺口高度均会显著降低壳程流体出口压降。

Figure 12. Effect of transverse tube spacing on pressure drop

图12. 横向管间距对压降的影响

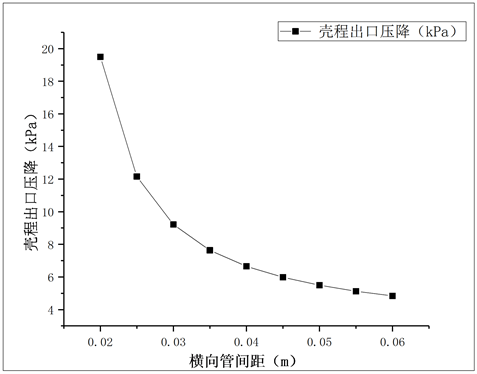
Figure 13. Effect of longitudinal tube spacing on pressure drop

图13. 纵向管间距对压降的影响

Figure 14. Effect of baffle spacing on pressure drop

图14. 折流板间距对压降的影响

图16给出了冷却器壳程流体流量对壳程流阻压降的影响，随着壳程流体进口流量的增大，壳程压降逐渐增大，呈非线性变化。

4. 结论

本文研究了管壳式冷却器两相流动传热及压降特性，给出了适用于该冷却器壳程出口温度及压降的计算表达式，并考虑了其壳程热流体的相变影响，数值结果与已有实测数据进行了对比验证，进一步分析了结构参数对其壳程出口温度及压降的影响，得到下述结论。

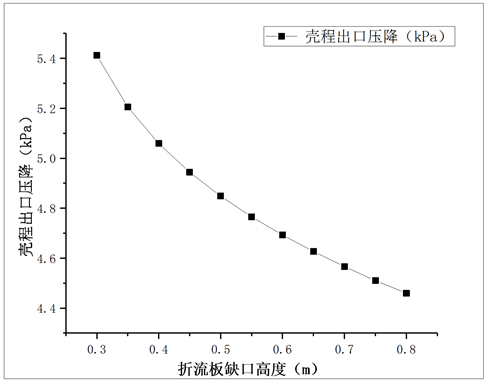
Figure 15. Influence of baffle notch height on pressure drop

图15. 折流板缺口高度对压降的影响

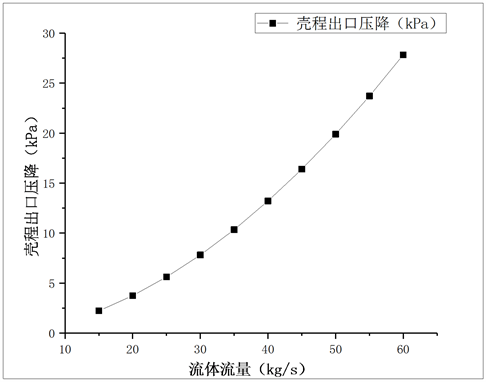
Figure 16. Effect of fluid flow on pressure drop

图16. 流体流量对压降的影响

冷却器壳程出口温度随管程介质密度的增加而增加，同时随换热管的外径增大而减小。

换热管和折流板的间距及其缺口高度对壳程的流阻压降影响显著，壳程压降随换热管横向及纵向管间距、折流板间距及缺口高度的增大而减小，随壳程流体流量的增大而增大，呈非线性变化。

由于实际工况中壳程热流体流动及换热情况比较复杂，为考虑换热器与外界的热交换及内部实际两相流动情况，在之后的分析中应考虑到包括热对流的实际换热模型及其它两相流动因素的影响，进一步提出更精确的壳程出口温度及压降理论模型。