1. 引言
骨架线 [1] 又称中轴线,是对图形几何形态的一种重要拓扑描述,能够简洁表示物体的形状,减少物体描述的信息量,并保持原图形的拓扑结构,具有重建性 [2] 以及对称性 [3]。图像的骨架也是描述图像几何及拓扑性质的重要特征,并被广泛应用于计算机视觉、生物形状描述、模式识别、工业检测、地理信息系统制图 [4] [5] 以及测绘和GIS领域研究 [6] [7] 等方面。确定一个物体的骨架是非常复杂的,关键在于提取方法的选取。骨架的提取总体来说有三类算法:第一类是Voronoi图法 [8],如面状要素提取;第二类是变换法,如中轴变换、形态变换、草原火变换;第三类是偏微分方程法 [9],如双曲定向偏微分方程 [10]。现在广泛使用的提取方法是图像灰度阈值化法和图像极值跟踪法,但是这两种算法通常需要在提取前进行几步处理,因而只在提取一些结构相对简单的骨架线时能够得到较好的结果,对复杂图像的骨架提取结果不是很理想。Snakes梯度算法结构上并不需要进行传统骨架线提取所普遍采用的滤波、二值化、腐蚀等过程,很好地解决了传统骨架线提取算法在提取具有复杂结构的多边形 [11]、噪声较大的图像时所表现出的精度低、分叉 [12] [13]、桥连、过度细化等问题。该算法在计算过程中很好地计算出了图像特征,但是在提取过程中对一些细节不能精确完成。本文将采用一种简单的方法使该算法对细节的处理更加准确,能够很好地解决原问题中存在的矛盾。
2. 基于Snakes的GVF骨架线提取算法
利用梯度矢量场gradient vector field (GVF)提取骨架线的过程主要分为三步:首先通过GVF snakes模型产生一个梯度矢量场 [14];然后对梯度矢量场做拓扑分析,使用技术提取和可视化拓扑信息 [15],寻找临界点;最后再利用矢量场中的通量筛选出符合条件的临界点,综合以上三步即可提取出骨架线。
Snakes算法 [16],也称为主动轮廓算法,由Kass等人在1987年首次提出,该算法通过取定合适的初始值,能量函数最小化 [17] 来达到接近目标区域轮廓的目的。该算法的出现,使Snakes模型可以有效地应用于边缘检测和轮廓提取 [18],从而正式让形变模型在图像分割上的应用一跃成为极具活力的研究领域。梯度矢量场最早是Xu和Prince等人以经典Snakes模型为基础,根据Helmholtz定理提出的,并建立了GVF Snakes [14] 模型。在经典的可变形模型算法中只是包含静态场,而根据Helmholtz理论,可将一般的静态矢量场分解为一个同时包含无旋成分和无散成分的梯度矢量场,并设计了一个被称为梯度矢量力的外力,进而计算出图像的梯度场。
从经典Snakes模型的能量方程,得到了相应的Euler方程:
(1)
Xu和Prince等人,将经典Snakes模型的Euler方程看成是一个内外力的平衡方程,即:
(2)
其中,
,
。以此为出发点,Xu和Prince等人提出了梯度矢量流外力场 [14]。它通过极小化如下能量函数得到:
(3)
再由变分法得到的Euler方程的解就成为式(3)取极小值的必要条件,其相应的Euler方程为:
(4)
拓扑概念在本算法中具有非常重要的意义,它是用来把几何问题数字化的工具,也是提取骨架的核心部分。我们把能体现图像特征的特殊点称作临界点,在临界点
附近,由矢量场的泰勒级数可知,GVF场的行为主要取决于GVF场的一阶偏导数,也就是说,临界点的雅克比矩阵可以用来表示矢量场的行为。
(5)
最后,根据雅克比矩阵的两个特征值之间的关系提取出不同的特征点。临界点一般可分为鞍点、结点和临界点,如图1所示,其中m、l为雅克比矩阵的特征值。
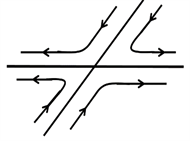 (a) 鞍点μ < 0 < λ
(a) 鞍点μ < 0 < λ 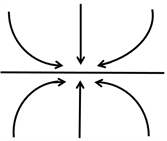 (b) 结点μ < λ < 0
(b) 结点μ < λ < 0 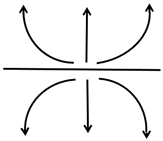 (c) 排斥点0 < μ < λ
(c) 排斥点0 < μ < λ
Figure 1. Critical point classification
图1. 临界点分类
在梯度矢量场中定义了一个新的物理量:通量,并结合上述拓扑分析方法作为提取骨架线的指标之一。梯度矢量场中的通量被定义为:每秒钟从闭合曲面流出的净流量。如果通量不等于零,表示闭合曲面内有源或汇。
3. 区域划分拓扑分析的GVF骨架线提取算法
3.1. 基于拓扑分析的GVF骨架线提取算法
由图2圆环模型的结果可知,基于拓扑分析的GVF骨架线 [19] 提取算法在处理亮暗分布均匀或灰度等级划分均匀的简单灰度图时效果很好,这也符合算法本身的原理。骨架线的提取是建立在原图的GVF场之上,而GVF场是对原图计算的梯度,灰度等级划分均匀也就表示梯度平滑,因此在提取骨架线时效果很好,在保留图像特征的基础上可以准确找到骨架线位置。
但对于图3这样灰度分布不均匀的复杂结构图像来说,亮暗差别明显,随即带来梯度突然增大的情况。在相同等级的通量下分布均匀的地方提取结果正常,而分布不均匀的地方提取结果容易出现断点。在该过程中,我们发现断点和噪点相互矛盾,当提取结果想要减少某一方时,另一方则会增多。通过梯度矢量场已经得到了图像特征,如图3(b),骨架线基本提取完整,即图像特征计算阶段已完整计算出所有骨架特征,但在提取阶段却存在上述矛盾。为了解决这一矛盾,在提取图像阶段,可以尝试换一种方式来解决。
 (a) 圆环模型
(a) 圆环模型 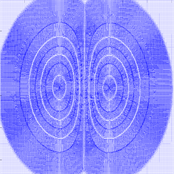 (b) GVF
(b) GVF 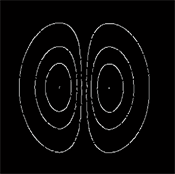 (c) 骨架线
(c) 骨架线
Figure 2. Original image, GVF and skeleton line of ring model
图2. 圆环模型的原图、GVF和骨架线
 (a) 原图
(a) 原图  (b) GVF
(b) GVF  (c) 骨架线(断点多)
(c) 骨架线(断点多) 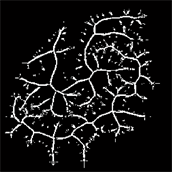 (d) 骨架线(噪点多)
(d) 骨架线(噪点多)
Figure 3. Original image, GVF and skeleton line of complex structure model
图3. 复杂结构模型的原图、GVF和骨架线
3.2. 区域划分拓扑分析的GVF骨架线提取算法
针对图3复杂结构模型出现的问题,在计算图像通量时,可以将图像通量划分出等级,通过不同等级的通量提取原图像的骨架线。经过大量的实验,根据结果发现:在低等级段位,骨架线由所有的结点和鞍点构成,但有些结点与鞍点却是不必要的,也就是在骨架线之外的过渡点,在图像中表现为噪点。而在高等级段位,提取出的点是结构清晰的结点与鞍点,除此以外的点都被剔除,这也是我们最终想要得到的结果,即图像的骨架线。
原拓扑提取方法是对平面在某种程度上做出整体提取,而现在用的方法是将整个图像划分为多个小区域,在每个区域上做出拓扑提取。在对总图进行划分的同时,一旦出现噪点与断点的矛盾,便再次进行划分。通过逐次划分,依次提取,直到最后在完整的图像特征上提取出完整的骨架线。下面是基于区域划分拓扑分析复杂图像的骨架线提取结果。
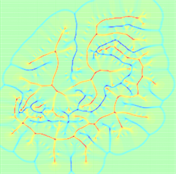 (a) 俯视图
(a) 俯视图 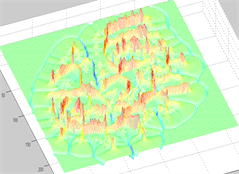 (b) 立体图
(b) 立体图
Figure 4. Flux level map of complex structure
图4. 复杂结构的通量等级图
图4为图3(b) GVF的通量等级图。图4(a)与图4(b)中红–绿区域为结点的通量级,绿–紫区域为排斥点的通量级。图5是复杂图像通量提取结果对比图,其中(a)为原通量提取结果,(b)为现通量提取结果,很明显新的提取方式得到的结构特点和分布趋势更加明显,通量趋势表达更加精细。
 (a) 原通量提取方式
(a) 原通量提取方式  (b) 现通量提取方式
(b) 现通量提取方式
Figure 5. Comparison of flux extraction methods for complex image
图5. 复杂图像通量提取方式对比图

Figure 6. Skeleton line extraction results based on region partition topology analysis
图6. 基于区域划分拓扑分析的骨架线提取结果

Table 1. Comparison of two algorithms for skeleton extraction
表1. 两种算法骨架线提取结果比较
在骨架线提取过程中,计算出的梯度矢量场(GVF)可以完全体现图像的特征。经过区域划分后,再用拓扑分析,提取出适合的可视化信息点 [20],一步一步组成区域,区域组成图形,由此提取出的骨架线即为完整的骨架线。通过表1对比图3和图6的提取结果,可知原方式提取过程中断点与噪点成相对状态,而且无论怎么调整,两类点中都会有一方出来干扰图像。改进处理方法后断点与噪点没有任何关系,数值上都较低,对图像的影响大大减少。理论上区域划分至无穷小时,就会变成对点的提取,又一次回到了最初的提取状态。因此该方法也存在一定的局限性,在相对的区域上可以完成相对的提取,一旦把区域放到无穷大或无穷小,又会回到最初的提取方式。所以划分区域取值的两个端点是不可取的。因此,对于大部分图像来说,无论简单还是复杂,无论亮暗分布是否均匀,只要区域划分细致合理,通量提取程度适中,都可以提取出图像的完整骨架线。
4. 结论
对于原GVF算法提取过程中的三个阶段,根据以往的研究可知,第一阶段中计算GVF矢量场时,图像的骨架特征都已显示出来,所以本文主要讨论第二和第三阶段可以做的一些改进。用区域划分方式来进行预处理,并协同拓扑分析与通量提取,做出循环式区域提取,这样可以得到更加完整的骨架图,得出的结果更为准确,解决了之前噪点与断点之间的矛盾,进一步地优化了算法结构。本算法在处理难度较大的光学图像时表现出显著效果,可以在医学图像分析、工程检测、光信息提取等方面发挥重要作用。
基金项目
天津市教委科研计划项目(项目编号:2017KJ028)。
NOTES
*通讯作者。