基于小波变换的电磁轴承故障信号诊断

Wavelet Transformation Fualt Diagnosis of Acitve Magnetic Beraings Based on Wavelet Transformation

摘要: 电磁轴承故障信号中电磁振动成分和机械振动成分相互耦合，呈现较强的非平稳性。以傅里叶变换(FFT)为基础的传统频域分析方法无法满足分析的需要，对此提出小波变换对电磁轴承故障信号进行频谱分析，本文基于小波变换，对原始信号进行多层次分解，有效地从电流信号中剥离高强度噪声，强化故障特征表达，为磁轴承故障诊断提供更为有效的数据信号。仿真结果表明利用小波变换能够检测出FFT不能检测出的故障信号。

Abstract: The electromagnetic vibration and the mechanical vibration in the active magnetic bearing (AMB) fault signal are coupled with each other, which are strong non-stationarity. The traditional frequency domain analysis method based on Fourier transform (FFT) cannot meet the needs of analysis. In this regard, wavelet transform is proposed to analyze the frequency spectrum of the electromagnetic bearing fault signal. Based on wavelet transform, this paper decomposes the original signal at multiple levels, effectively separates the high-intensity noise from the current signal, strengthens the fault feature expression, and provides a more effective data signal for magnetic bearing fault diagnosis. The simulation results show that the use of wavelet transform can detect fault signals that FFT cannot detect.

1. 引言

电磁轴承(Active Magnetic Bearing, AMB)是利用电磁铁与铁磁材料之间的可控电磁引力实现对转子的无接触支承，具有无摩擦、适合高速运行以及使用寿命长等优点，因此广泛应用于高速发电机、分子泵、压缩机、飞轮等高速旋转机械 [1] [2] [3]。电磁轴承集机械、电磁、控制于一体，存在系统复杂、可靠性不高、易受电磁、环境条件干扰等不足，存在失稳等安全隐患，增加了故障概率 [4]。磁轴承系统中的典型故障包含转子不平衡、轴系不对中、转子弯曲、裂纹、冲击、定转子碰磨、转速突变、电磁线圈绝缘、位移传感器故障等。为了提高磁轴承故障诊断的可靠性和效率，学者对诊断方法进行了深入研究，提出了基于D-S信息融合技术的故障诊断 [5]、基于虚拟仪器(LabVIEW)的故障诊断 [6]、基于广义似然比检验的位移传感器故障识别 [7]、基于电流特性的电磁线圈故障诊断 [8]，主要集中在轴承机械振动故障诊断领域，基于电信号分析的故障诊断少见报导。

电磁轴承故障信号中机械振动成分和电磁成分相互耦合，呈现较强的非平稳性。以电磁轴承支承的高速电机为例，相比传统的机械轴承，磁轴承的工作气隙大，支撑刚度低，轴承转子的机械故障导致电机定子磁场不对称及相电流频谱异，当相电流受干扰，其相电流的频率成分复杂，本文以电机定子相电流为表征信号进行磁轴承故障的特征提取。在时域分析中，过零点已被引入传统机械轴承故障诊断 [9]，以傅里叶变换(FFT)为基础的传统频域分析方法、小波分析和经验式分解(EMD)等已被运用于识别机械轴承故障。轴承故障诊断是一个关于如何在提取特征向量后建立智能评模型的问题，近年来发展了较多基于小波分析的轴承故障分类算法，包括RBF神经网络 [10]、改进分形网络 [11]、层次熵的D-S证据理论 [12]、支持向量机 [13] 等。为了提取由磁轴承故障产生的定子相电流非平稳信号特征，本文基于小波变换，对原始信号进行多层次分解，有效地从电流信号中剥离高强度噪声，强化故障特征表达，为磁轴承故障诊断提供更为有效的数据信号。

2. Haar小波变换

小波变换是在傅立叶变换的基础上发展起来的，是一种具有能量的微小波动，其能量集中于某一时间及频率上，它是对瞬时、不平稳或时变信号进行分析的合适的工具。传统傅立叶变换将能量有限的信号分解到一组正交基上，这组正交基是在给定的信号函数空间上稠密的，短时傅立叶变换则在正交基上加上时间窗，即把分解后的信号再进行一次分解。不同于传统傅里叶变换实现信号时域和频域之间的整体变换，同时也不同于短时傅里叶变换窗长固定，小波变换可以根据信号自适应的调整时间–频率窗，信号在一组正交基函数上的分解，其中基函数通过母小波的尺度伸缩和平移得到。

小波函数为

$W_f\left(\beta ,\tau \right)=\frac{1}{\sqrt{\left|\beta \right|}}{\displaystyle {\int }_{-\infty }^{+\infty }f\left(t\right)\phi \left(\frac{t-\tau }{\beta }\right)\text{d}t}$ (1)

式中， $f\left(t\right)$ 为给定信号， $\beta$ 和 $\tau$ 为整数， $\beta$ 为尺度因子，对基函数进行伸缩， $\tau$ 则反映基函数的平移。通过调整这些小波参数，可实现对基函数的伸缩和平移，形成小波簇。小波分解结果为 [14]

$f\left(t\right)={\displaystyle \underset{\tau =-\infty }{\overset{+\infty }{\sum }}a\left(\tau \right)\psi \left(t\right)}+{\displaystyle \underset{\tau =-\infty }{\overset{+\infty }{\sum }}d\left(\tau \right)\varphi \left(t\right)}$ (2)

式中， $\psi \left(t\right)$ 是尺度函数； $\varphi \left(t\right)$ 是母小波。小波变换对信号进行分析可以从滤波器组的角度进行理解。在式(2)中，与 $\psi \left(t\right)$ 是相关联的低通滤波器，式中第一部分求和是原始信号的平滑，包含了低频信息；同理 $\varphi \left(t\right)$ 是相关联的高通滤波器，式中第二部分求和包含了原始信号的细节信息。

图1给出了三级小波分解的结构示意图，第一级分解将原始信号分解为低频部分 $a_1$ 和高频部分 $d_1$ 。第二层分解中将 $a_1$ 作为输入，得到低频部分 $a_2$ 和高频部分 $d_2$ ，依次类推得到 $a_3$ 和 $d_3$ 。

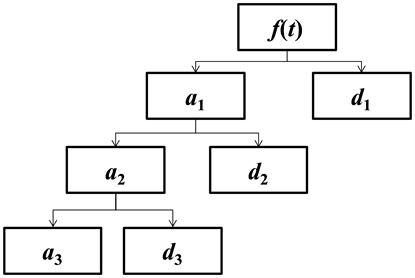
Figure 1. Example of three-level wavelet decompositon

图1. 三级小波分解示例

常见的正交基函数有许多种，哈尔基函数(Haar basis function)具有计算快速，正交特性好的优点被广泛应用。Haar小波函数是定义域在 $t\in \left[0,1\right)$ 半开区间上的单个矩形波。其取值具有间断性，在一段区间内取值为零。Haar 函数的缩放函数和母函数为：

$\psi \left(t\right)=\{\begin{array}{cc}1& 0\le t<1\\ 0& else\end{array},\varphi \left(t\right)=\{\begin{array}{cc}1& 0\le t<1/2\\ -1& 1/2\le t<1\\ 0& else\end{array}{\varphi }_{\alpha ,\tau }\left(t\right)$ (3)

Haar小波分解可以通过Mallat算法实现，将原始信号先分解成近似信号和细节信号，然后把分解得到的近似信号继续分解为近似信号和细节信号，依此类推，可以分解到n层的近似信号和细节信号。

3. 电磁轴承电机振动

以电磁轴承支撑的高速电机为例，作用在电机上的电磁力有多种类型，这里主要考虑作用在定子铁心内表面和转子外表面上的径向电磁力。电磁力的作用形式可以表述为：

$F_{air}=F_m\sin \left(p\alpha +2\text{π}ft+{\alpha }_0\right)$ (4)

式中，F_m为电磁力幅值(单位：N/m²)，指整个定子铁心内表面的单位面积的径向力(或转子铁心外表面的单位面积的径向力)；p为电磁力阶数，指电磁力沿定子铁心(或转子铁心)圆周方向的周期数；f为电磁力的频率，如以负号表示逆时针旋转，正号表示顺时针旋转； ${\alpha }_0$ 电磁力的相位(用弧度表示)；t为时间变量， $\alpha$ 为空间变量，表示沿定子铁心(或转子铁心)圆周的机械角度。

根据结构动力学理论，系统动力学平衡方程为：

$\left[M\right]\left\{\ddot{x}\right\}+\left[C\right]\left\{\stackrel{\dot{}}{x}\right\}+\left[K\right]\left\{x\right\}=\left\{F\left(t\right)\right\}$ (5)

根据交流电机的绕组理论和电机电磁振动的相关理论可知，引起电磁振动的主要原因是电机气隙磁场对定子和转子作用的径向磁拉力。径向磁拉力正比于相电流，并且频率是相电流频率的2倍，即振动信号频率是电流频率的两倍，并且随着电流的减小而较小。

当相电流受干扰进，其相电流的频率成分复杂。在分析中，将相电流信号进行小波多级分解，其中低频部分是表征信号本身特征的，而高频部分则是表征信号的细微差别。小波变换得到的近似信号是电流轴承正常状态下的信号，而细节信号表征的是轴承的故障信号。

4. 算例

本文在电磁轴承平台上测量电机定子三相电流(基波频率为50 Hz)波形如图2所示。该原始信号为电磁轴承故障时的信号，故障频率为高频。

Figure 2. Three-phase current signal

图2. 三相电流信号

采用传统FFT分析电流信号的频谱如图3所示，为了便于观察，降低了基波幅值。由图3可知，原始信号中除了基波成分外，还存在3、5、7次谐波成分，但无法分析更高频段的电磁轴承故障信号。

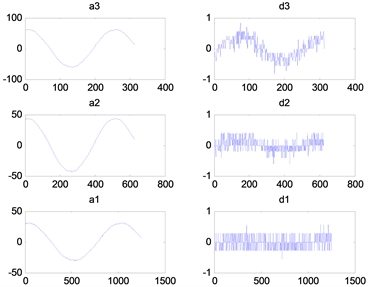
图4为三相电流的Haar小波三级分解。分解后分别得到高频部分和低频部分，其中a1~a3表示代低频部分本征信号，高频d1~d3表示高频部分细节信号。

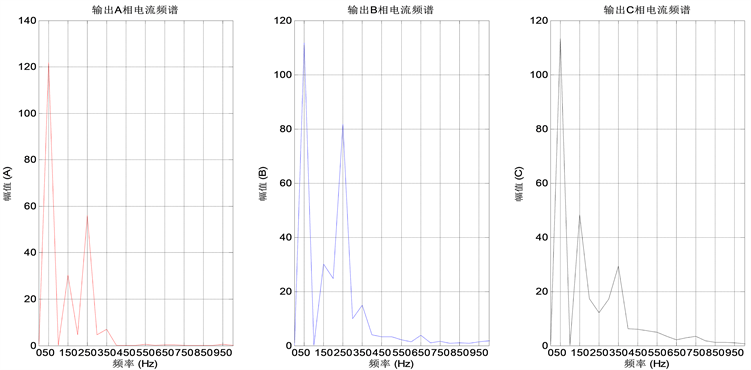
Figure 3. The frequency spectrum of the three-phase current signal (FFT)

图3. 三相电流信号的频谱(FFT)

A相 B相C相

Figure 4. Three-phase current wavelet decomposition (Haar)

图4. 三相电流小波分解(Haar)

为了进一步提取故障频率，对小波的三层细节信号d1~d3做FFT谱分析，结果如图5所示。由图5

A phase signal spectrum B phase signal spectrumC phase signal spectrum

Figure 5. Wavelet signal spectrum (d1~d3)

图5. 小波信号频谱(d1~d3)

可知，小波变换后的细节信号再经过FFT变换能够清晰地判断出振动信号的故障特征，说明Haar小波在电磁轴承故障时域波形分析时比传统FFT分析具有较大的优势。另外对低频信号a3进行FFT谱分析，a3为将高频部分去掉后最本征的信号。如图6所示(为便于观察，未显示基波信号频点)。

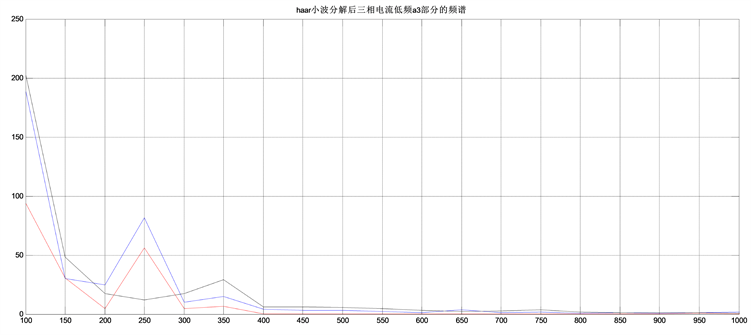
Figure 6. Wavelet signal spectrum (a3)

图6. 小波信号频谱(a3)

5. 结论

本文以发电机用电磁轴承为研究对象，运用小波变换对其进行故障诊断。仿真计算表明：电磁轴承故障信号高频部分可通过Haar小波变换判别。利用小波变换的多分辨率分析技术和对细节信号进一步谱分析，对电磁轴承故障信号行处理可获得高频的故障信号，比传统的基于傅立叶变换的频谱分析技术具有更好的实用性。小波变换是处理非平稳信号的一种有效处理手段，也是一种有效的电磁轴承故障诊断方法。

参考文献