基于生存分析的口腔鳞状细胞癌患者研究

Oral Squamous Cell Carcinoma Patient Study Based on Survival Analysis

摘要: 本文基于生存分析方法对口腔鳞状细胞癌患者特点及预后影响因素研究。首先利用参数估计和非参数估计对生存函数进行估计，了解其特点；然后基于COX模型，以死亡时间为因变量，分别以年龄、肿瘤阶段及性别为因变量建模，分析生存时间影响因素。研究结果表明将死亡的时间和年龄、肿瘤阶段以及性别建立的模型有效，得出影响口腔鳞状细胞癌患者死亡时间的主要因素为年龄、肿瘤阶段以及性别。

Abstract: Based on the survival analysis method, the characteristics and prognostic factors of patients with oral squamous cell carcinoma were studied. Firstly, the survival function is estimated by parametric estimation and nonparametric estimation to understand its characteristics. Then, based on COX model, time of death was used as the dependent variable, and age, tumor stage and gender were used as the dependent variable to analyze the factors affecting survival time. The results showed that the model of time of death and age, tumor stage and gender was effective, and the main factors influencing the time of death of patients with oral squamous cell carcinoma were age, tumor stage and gender.

1. 引言

口腔鱗状细胞癌(OSCC)是目前为止非常常见的恶性肿瘤，其每年的发病率逐渐升高，同时许多因素会影响口腔鳞状细胞癌患者的生存时间，因此，明确口腔鳞状细胞癌患者的特点和影响其生存时间的因素对于提高患者生存质量有重要意义。

许多学者对影响口腔鳞状细胞癌患者预后的因素进行了分析，其中，张华、杨蓉 [1] 等人利用SPSS20.0及STATA软件对389例初诊OSCC患者的临床病理及随访资料进行了统计学分析，发现OSCC 5年生存率相对较低。中晚期患者淋巴结外侵犯明显，严重影响预后。早期发现和诊治可降低OSCC复发率，从而提高患者生存率；王立业 [2] 等人对口腔鳞状细胞癌患者预后相关基因标志物的生物信息学进行分析；张泽军、南欣荣、闫星泉 [3] 等人探讨临床III~IV期口腔鳞状细胞癌患者术后复发的危险因素和复发患者的预后状况，采用单因素和多因素Logistic回归分析研究影响患者术后复发的危险因素，以及单因素和多因素生存分析研究复发患者的预后状况，发现III~IV期患者复发率较高且复发后预后不佳，淋巴结比率和神经侵犯时影响复发的不良特征；霍玉荣、康鹏 [4] 等人分析了口腔鳞状细胞癌患者生存及复发的临床影响因素，采用Logistic回归分析了88例口腔鳞状细胞癌患者的临床资料，发现口腔鳞状细胞癌患者预后并不理想；以及Y.K [5] 等人研究了在台湾南部703人口腔鳞状细胞癌预后因素。在这些研究中，大多数学者采用单因素分析、多因素分析等方法对患者预后因素进行研究，而对于口腔鳞状细胞癌患者生存时间及其影响因素的研究还比较少，因此本文考虑采用生存分析的方法对患者进行研究。

2. 口腔鳞状细胞癌患者的生存分析

2.1. 研究数据

本文研究的数据为orca数据集，我们对1985.1.1到2005.12.31这个时间段中芬兰最北部省份诊断结果为口腔鳞状细胞癌的338名患者进行研究。本次研究的患者的随访开始日期为癌症诊断当天，并且患者于2008.12.31死亡，迁移或随访截止日期结束。造成患者死亡原因主要有两种：1) OSCC死亡；2) 其他原因造成的死亡。

2.2. OSCC患者生存数据分析

生存分析主要关注于事件数据的时间，在本文中，为诊断后的死亡时间。

为了明白该数据的特点以及其主要形式，我们首先对OSCC患者进行生存数据分析，如图1所示，其中图1左半部分为受试者随访时间与事件的关系，右半部分为受试者随访时间与年龄的关系：

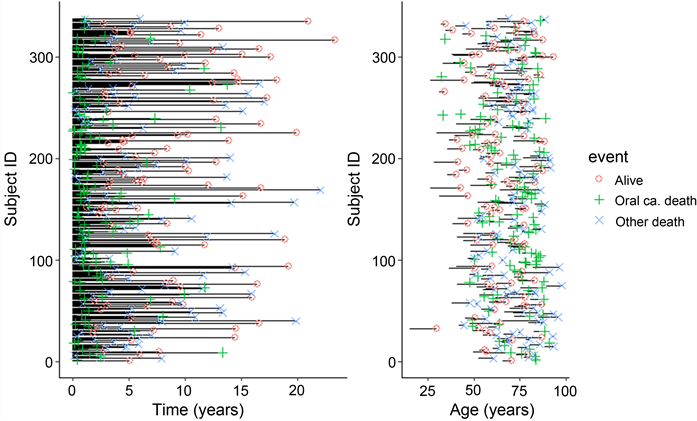
Figure 1. Relationship between follow-up time and event and age

图1. 受试者随访时间与事件和年龄的关系

从上述左图我们可以看出，在随访事件内，因口腔鳞状细胞癌死亡的受试者大多发生在早期，即早期OSCC疾病引起的死亡率较高，而不是由于其他原因引起的死亡。从上述右图可以看出，因口腔鳞状细胞癌死亡的患者大多集中在中老年段和老年段，中老年人和老年人抵抗力弱，产生抗体的能力弱，所以更容易死亡。

2.3. OSCC患者生存函数估计

2.3.1. 非参数估计

1) Kaplan-Meier估计：

K-M方法即乘积极限法，是一种统计描述方法，充分的利用了信息，给出了准确的统计量。假设在r个生存时间中有J个死亡时间： ${\tau }_1<\cdots <{\tau }_j<\cdots <{\tau }_J$ .令 ${\tau }_0=0$ ，用 ${\tau }_{J+1}$ 表示最大存活时间。对删失生存数据的Kaplan-Meier方法首先以死亡时间为切入点讲随访期划分为 $J+1$ 个区间： $\left[{\tau }_0,{\tau }_1\right),\left[{\tau }_1,{\tau }_2\right),\cdots ,\left[{\tau }_j,{\tau }_{j+1}\right),\cdots ,\left[{\tau }_{J-1},{\tau }_J\right),\left[{\tau }_J,{\tau }_{J+1}\right]$ 。设 $a_j$ 表示在第j个区间 $\left(j=0,1,\cdots ,J\right)$ 中的死亡人数，根据定义 $a_0=0$ ；设 $r_j$ 表示第j个风险集合 $\left(j=0,1,\cdots ,J\right)$ 中的受试者数，并用 $r_{J+1}$ 表示存活到 ${\tau }_{J+1}$ 的受试者数；设 $p_j$ 表示在给定存活到 ${\tau }_j-\epsilon \left(j=0,1,\cdots ,J\right)$ 时，存活到 ${\tau }_j+\epsilon$ 的条件概率。

基于上述划分和某些条件概率推导出生存概率 $S\left(T\right)$ 的估计如下：

${\hat{S}}_j={\hat{p}}_1{\hat{p}}_2\cdots {\hat{p}}_j$

生存函数的K-M估计见图2。

从下述的K-M生存曲线图中，可以得到每个时间点的生存概率。在早期时，陡峭的K-M曲线，说明在这一段时间内，死亡人数多，也证实了生存数据分析板块中，早期口腔鳞状细胞癌患者的高死亡率；在中期时，K-M曲线逐渐平稳，生存率下降趋势渐渐变缓；在后期时，K-M曲线基本平稳，生存率不会有大幅度的下降。

Figure 2. K-M survival curve

图2. K-M生存曲线图

2) Nelson-Aalen估计：

Nelson-Aalen估计是一种应用于生物统计学中对生存性概率分析的非参数估计方法，其根本的思想为依据累计的失效率函数对累计死亡率进行估计。本文研究数据的N-A估计表见表1：

Table 1. N-A estimation table

表1. N-A估计表

3) Life-table：

生命表又称“死亡率表”，其根据年龄划分的死亡率进行编制，描述了一批人从出生后陆续死亡的全部过程的一种统计表，其主要的内容有：① 当年生存者的年龄；② 在划分年龄组中的死亡人数；③ 在划分年龄区间的条件死亡概率；④ 在划分年龄区间的生存条件概率；⑤ 生存到年龄为x的人数。

本文研究数据的生命表结果见表2：

Table 2. Life table

表2. 生命表

2.3.2. 参数估算器

1) 指数模型：

设数据来自指数分布，其概率密度函数为：

$f\left(t\right)=\{\begin{array}{l}\lambda {\text{e}}^{-\lambda t}t\ge 0,\lambda >0\\ 0t<0\end{array}$

分布函数： $F\left(t\right)=1-{\text{e}}^{-\lambda t}\left(t\ge 0\right)$

生存函数： $S\left(t\right)=1-F\left(t\right)={\text{e}}^{-\lambda t}$

危险函数： $h\left(t\right)=\frac{f\left(t\right)}{S\left(t\right)}=\lambda \text{,}\lambda >0,t\ge 0$

2) Weibull模型：

Weibull模型的相关函数如下。

生存时间T的概率密度函数： $f\left(t\right)=\lambda \gamma {\left(t\right)}^{\gamma -1}\exp \left[-\lambda {\left(t\right)}^{\gamma }\right]$

分布函数： $F\left(t\right)=1-\exp \left[-\lambda {\left(t\right)}^y\right]$

生存函数： $S\left(t\right)=\exp \left[-\lambda {\left(t\right)}^r\right]$

危险函数： $h\left(t\right)=\lambda \gamma {\left(t\right)}^{\gamma -1}$

3) log-logistic模型：

log-logistic模型称为双对数模型。三种模型的曲线对比图见图3：

Figure 3. Comparison diagram of model curves

图3. 模型曲线对比图

从图3右半部分图形可以看出，三种模型的生存曲线在随访时间0~10年期间的趋势比较接近，但是在随访时间10年之后的曲线有明显差异。从上述左图可以看出，指数分布的危险函数曲线为一条平行于x轴的线；而log-logistic模型的危险函数曲线，具有非常明显的下降趋势；Weibull模型的危险函数曲线较log-logistic模型更为平缓，但两种模型都在随访时间7年左右下降趋势明显。

2.4. 生存曲线比较

2.4.1. 肿瘤阶段生存曲线比较

肿瘤阶段是常见的医学指标，在此我们对不同肿瘤阶段的生存曲线进行比较，判断肿瘤阶段是否为癌症存活研究中的重要影响因素。

从图4中我们可以看出，不同肿瘤阶段的生存曲线图有明显的差异，几乎没有重叠的部分，可能为癌症存活研究中的重要影响因素。

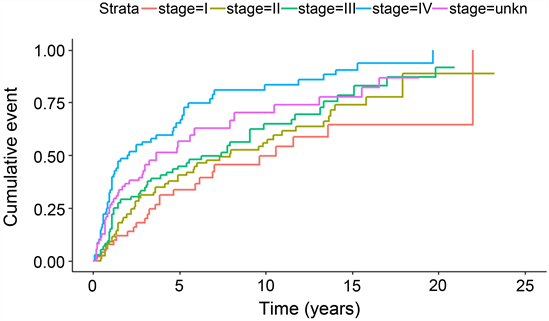
Figure 4. Comparison of survival curves at different tumor stages

图4. 不同肿瘤阶段的生存曲线对比图

2.4.2. Mantel-Haenszel Logrank检验

肿瘤阶段的M-H logrank检验结果见表3：

Table 3. M-H test results

表3. M-H检验结果表

从检验的结果来看，检验的P值为0.00002，在 $\alpha =0.05$ 的检验水平下，显著的拒绝原假设，所以没有充分的理由拒绝肿瘤阶段是癌症存活研究中的重要影响因素。从上述肿瘤阶段的生存曲线图也可以看出，低肿瘤阶段的癌症患者生存率要明显低于高肿瘤阶段的癌症患者，说明口腔鳞状细胞癌患者的早期死亡率高。

3. 模型

3.1. 建立模型

我们比较单个的因子水平的生存函数时，利用非参数检验非常有效。但是当我们需要检验因素的数量增大时，上述方法将会变得难以进行。所以，在此我们可以利用回归模型来发现生存和预测因子之间的关系。在此我们选择CoxPH模型 [6] 进行建模。我们考虑将死亡的时间和性别、年龄和肿瘤阶段进行建模。建模结果见表4：

Table 4. CoxPH modeling results

表4. CoxPH建模结果

从Cox模型的结果可知，性别，年龄和阶段对模型具有显著影响。我们从估计中发现，第一阶段和第二阶段的差异非常微小；而对于未知阶段的群体来说，可能是来自不同阶段患者的混合，所以，我们可以将第一阶段和第二阶段进行组合。

3.2. 模型检验

3.2.1. 似然比检验、Wald检验、Score检验

对CoxPH建模结果，即死亡时间建模为性别功能、年龄和肿瘤阶段是否合理进行似然比检验、Wald检验、Score检验，检验结果见表5：

Table 5. Test results

表5. 检验结果

分别从三种检验结果的P值可知，其P值都远小于显著性水平0.05，所以该模型显著。选择年龄、肿瘤阶段以及性别建立模型是有效的。

3.2.2. 变量检验

除了对模型进行检验，还需要使用函数分别检查数据与功能性别、年龄和肿瘤阶段变量的比例风险假设是否和全局一致。检验结果见图5：

Figure 5. Test results

图5. 检验结果

从上图中，我们可以看见其P值都明显大于显著性水平0.05，没有充分的理由拒绝原假设，所以每个变量的比例风险假设分别和全局一致。

3.2.3. 图形化比较多变量

由于在CoxPH结果中，第一阶段和第二阶段没有明显变化，在此选取森林图，将第一阶段和第二阶段合为一个变量进行绘图与第一阶段和第二阶段分别进行绘图进行对比，图6为对比结果：

Figure 6. Comparison of variables

图6. 变量对比

我们可以从上图发现，在图6左半部分图形中，第一阶段和第二阶段的图形非常接近，区别非常微小；在图6右半部分图形中，将第一阶段和第二阶段合为一个变量，其与其他变量的区别更为明显。所以可以将第一阶段和第二阶段合为一个变量进行建模。

3.3. 模型预测

逐步绘制预测的生存曲线，根据拟合的模型确定性别和年龄的值，图7为生存曲线拟合图：

Figure 7. Survival curve fitting

图7. 生存曲线拟合

在这里分别确定年龄为40和80，性别为女性和男性。年龄为80岁的患者，生存率明显低于年龄为40岁的患者，且年老者生存函数陡峭，下降比中年者更为迅速。而对于性别来说，女性的死亡率比男性更低。

4. 结论

本文通过采用生存分析方法对口腔鳞状细胞癌患者进行研究，建立了 回归模型，得出了以下结论：

1) 口腔鳞状细胞癌患者的特点

在上述的分析结果中，我们可以知道。在随访事件内，因口腔鳞状细胞癌死亡的受试者大多发生在早期，即早期口腔鳞状细胞癌疾病引起的死亡率较高，而不是由于其他原因引起的死亡。而因口腔鳞状细胞癌死亡的患者大多集中在中老年段和老年段，中老年人和老年人抵抗力弱，产生抗体的能力弱，所以更容易死亡。

2) 影响口腔鳞状细胞癌患者死亡时间的因素

本文利用Cox模型将死亡时间建模和性别、年龄以及肿瘤阶段进行建模，从检验的结果可以得出，其P值都远小于显著性水平0.05，所以该模型显著。由于其肿瘤第一阶段和第二阶段从图形分析上非常接近，于是便将两个阶段合并，采用随机森林图对合并前后进行对比，结果发现，合并后的效果更加优良，于是采用合并后的Cox模型，最后对模型进行预测，发现年龄、肿瘤阶段以及性别是影响死亡时间的重要因素。

NOTES

^*通讯作者。