中立型半马尔科夫跳跃系统的可达集边界估计

Reachable Set Boundary Estimations for Neutral Semi-Markov Jump System

摘要: 中立型半马尔科夫跳跃系统是许多动态系统中存在的时滞系统的一种特殊情况，其可达集估计问题具有理论和实践意义。研究的是具有实变时滞的中立型半马尔科夫跳跃系统的可达集边界问题。首先，构造新的李雅普诺夫泛函，利用Ito引理和Jensen不等式等矩阵不等式技巧，得到了一个较小的可达集边界。其次，用Matlab中的LMI控制工具箱对理论结果进行验证。最后，给出数值案例，说明结果的有效性。

Abstract: Neutral semi-Markov jump systems are a special case of time-delay systems in many dynamical systems, and the problem of the reachable set estimation has significance in theory and practice. In this paper, the reachable set problem for neutral semi-Markov jump systems with time-varying delays is considered. Firstly, the Lyapunov function is constructed, the no-ellipsoidal bound of the reachable set is as small as what is obtained by applied Ito’s Lemma and Jensen's inequality. Secondly, the LMI toolbox, in Matlab, is used to check the correctness of the results. Finally, numerical examples are given to verify the validity.

1. 引言

马尔科夫跳跃系统是一种特殊的混合随机系统且已经取得了大量的结果 [1] [2] [3] [4] ，然而马尔科夫跳跃系统的结果本质上是保守的，在实际应用中有许多限制，许多系统不能由马尔科夫跳跃系统建模。为了克服MJSs的局限性，在系统 [5] [6] [7] [8] [9] 中引入了半马尔科夫跳跃系统的概念。事实上，大多数马尔科夫跳跃系统的建模、分析和设计结果都是半马尔科夫跳跃系统的特殊情况。因此，对S-MJSs的研究在理论上和实践中都具有重要意义。系统的鲁棒稳定、随机稳定以及同步问题等问题的研究成果较少 [10] [11] [12] 。

由于时间延迟的存在，系统过去的状态将给当前系统状态带来延迟，并影响未来状态，从而导致系统的不稳定性和性能下降 [13] 。可达集估计问题具有理论和实践意义，在许多领域也有广泛的应用，如工程领域中飞机自动着陆机安全分析 [14] [15] 。半马尔科夫跳跃系统的可达集估计是一个相对较新的没有很大成就的领域，许多问题仍然值得探索。中立型系统是许多动态系统中存在的时滞系统的一种特殊情况。近年来，对于中立型系统的稳定性有了一些研究 [16] [17] [18] 。然而，具有有界峰值扰动的中立型系统的可达集边界的研究尚少。本文研究了具有实变时滞的中立型半马尔科夫跳跃系统可达集边界估计问题。基于李亚普诺夫–克拉索夫斯基型泛函和线性矩阵不等式，得到一个较小的可达集椭球边界，最后用数值算例验证了所得结果的有效性。

2. 问题描述

首先，考虑以下具有实变时滞的中立型半马尔科夫跳跃系统

$\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)-C_{\left(t,r_t\right)}\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)=A_{\left(t,r_t\right)}x\left(t\right)+B_{\left(t,r_t\right)}x\left(t-h\left(t\right)\right)+D_{\left(t,r_t\right)}\omega \left(t\right),\\ x\left(t_0+\theta \right)\equiv 0,\forall t\in \left[-h,0\right].\end{array}$ (1)

其中 $x\left(t\right)\in {\Re }^n$ 是状态向量， $\omega \left(t\right)\in {\Re }^m$ 是系统扰动，满足

${\omega }^{\text{T}}\left(t\right)\omega \left(t\right)\le {\omega }_m^2<1,$ (2)

$\tau \left(t\right)$ 是中立型时滞， $h\left(t\right)$ 是实变离散时滞，满足

$\begin{array}{l}0\le h\left(t\right)\le h,\stackrel{\dot{}}{h}\left(t\right)\le h_d<1,\\ 0\le \tau \left(t\right)\le \tau ,\stackrel{\dot{}}{\tau }\left(t\right)\le {\tau }_d<1,\end{array}$ (3)

其中 $h,h_d,\tau ,{\tau }_d$ 都是常数。 $A_{\left(t,r_t\right)},B_{\left(t,r_t\right)},C_{\left(t,r_t\right)},D_{\left(t,r_t\right)}\in {\Re }^{n\times n}$ 是已知含有状态转移概率的常数矩阵， $\left\{r_t,t\ge 0\right\}$ 为右连续半马尔科夫过程在有限概率空间及有限状态空间 $\zeta =\left\{1,2,\cdots ,N\right\}$ 的值，并且有状态转移概率矩阵 $\Lambda ={\lambda }_{ij}\left(h\right)$， $i,j\in \zeta$，描述如下

$\mathrm{Pr}=\left\{r_{t+\Delta }=j|r_t=i\right\}=\{\begin{array}{l}{\lambda }_{ij}\left(h\right)\Delta +o\left(\Delta \right),j\ne i,\\ 1+{\lambda }_{ij}\left(h\right)\Delta +o\left(\Delta \right),j=i,\end{array}$ (4)

这里 $h>0$ 表示驻留时间。 $\Delta >0$， $\underset{\Delta \to 0^{+}}{\lim }\frac{o\left(\Delta \right)}{\Delta }=0$ 且 ${\lambda }_{ij}\left(h\right)>0$ 表示从i时刻到j时刻的转移率且 ${\lambda }_{ii}\left(h\right)=-{\displaystyle {\sum }_{j=1,j\ne i}^N{\lambda }_{ij}\left(h\right)}$。实际上， ${\underset{\_}{\lambda }}_{ij}\le {\lambda }_{ij}\left(h\right)\le {\bar{\lambda }}_{ij}$，其中 ${\underset{\_}{\lambda }}_{ij}$ 和 ${\bar{\lambda }}_{ij}$ 都是常数且 ${\lambda }_{ij}\left(h\right)=\frac{f_{ij}\left(h\right)}{1-F_{ij}\left(h\right)}=\frac{{\lambda }_{ij}{\text{e}}^{-{\lambda }_{ij}h}}{1-\left(1-{\text{e}}^{{\lambda }_{ij}h}\right)}={\lambda }_{ij}$， ${\lambda }_{ij}$ 独立于h，这意味着马尔科夫跳跃系统是半马尔科夫跳跃系统的特殊情况。

半马尔科夫跳跃系统在连续时间内的转移概率取决于其转移率，本文考虑的转移率矩阵如下

$\Lambda \left(h\right)=\left(\begin{array}{cccc}{\lambda }_{11}\left(h\right)& ?& \cdots & {\lambda }_{1N}\left(h\right)\\ ?& {\lambda }_{22}\left(h\right)& \cdots & {\lambda }_{2N}\left(h\right)\\ ⋮& ⋮& \ddots & ⋮\\ {\lambda }_{1N}\left(h\right)& ?& \cdots & {\lambda }_{NN}\left(h\right)\end{array}\right)$ (5)

其中?表示未知的状态转移率。对于任意的 $i\in \zeta$，集合 $U^i=U_k^i\cup U_{uk}^i$

$\begin{array}{l}{U}_k^i\triangleq \left\{j:{\lambda }_{ij}未知,j\in \zeta \right\}\\ U_{uk}^i\triangleq \left\{j:{\lambda }_{ij}未知,j\in \zeta \right\}\end{array}$

此外，如果是 $U_k^i\ne 0$，它可被进一步描述为 $U_k^i=\left\{k_1^i,k_2^i,\cdots ,k_m^i\right\}$，其中m是一个非负整数，且 $1\le m\le N$， $k_j^i\in Z^{+}$， $j=1,2,3,\cdots ,m$ 表示状态转移概率矩阵 $\Lambda$ 中第i行和第j列的已知元素。

本文旨在找到一个满足条件(1)和(2)的中立型半马尔科夫跳跃系统的可达集，并表示为

${\Re }_x=\left\{x\left(t\right)\in {\Re }^n|x\left(t\right),\omega \left(t\right)\text{satisfy}\left(1\right)\text{and}\left(2\right)\right\}$ (6)

文献 [19] 提出这个可达集估计问题可以转化为寻找椭球体来约束 ${\Re }_x$ 的问题，可表示为

$\Im \left(P\right)\triangleq \left\{x\left(t\right)\in {\Re }^n:x^{\text{T}}\left(t\right)Px\left(t\right)\le 1,P>0\right\}$ (7)

为了简单起见，本文中 $A\left(t,r_t\right)=A_i$， $B\left(t,r_t\right)=B_i$， $C\left(t,r_t\right)=C_i$， $D\left(t,r_t\right)=D_i$， $F\left(t,r_t\right)=F_i$， $P\left(t,r_t\right)=P_i$。

3. 定理及引理

引理1 [19] 对于半马尔科夫跳跃系统(1)，若存在lyapunov函数 $V\left(x_t,t>0,r_t=i\right)=V\left(x_t,t,i\right)$ 满足以下等式

$LV\left(x\left(t\right),t,i\right)=\underset{\Delta \to 0^{+}}{\lim }\frac{1}{\Delta }\left[\epsilon \left(V\left(x\left(t+\Delta \right),t+\Delta ,r_{t+\Delta }\right)|x\left(t\right),r_t=i\right)-V\left(x\left(t\right),t,i\right)\right]<0,$ (8)

则系统(1)是稳定的。

引理2 [20] 存在条件 $V\left(t,x\left(0\right)\right)=0$ 且 ${\omega }^{\text{T}}\left(t\right)\omega \left(t\right)\le {\omega }_m^2$，如果

$LV\left(t,x_t\right)+\alpha V\left(t,x_t\right)-\beta {\omega }^{\text{T}}\left(t\right)\omega \left(t\right)\le 0,\alpha >0,\beta >0,$

则有 $V\left(t,x_t\right)\le \frac{\beta }{\alpha }{\omega }_m^2$ 对于任意 $t\ge 0$。

引理3 [21] 存在正定矩阵 $M\in {ℝ}^{n\times n}$，标量 $b>a>0$，向量函数 $\omega :\left[a,b\right]\to {\Re }^n$，则以下不等式成立

${\displaystyle {\int }_a^b{\omega }^{\text{T}}\left(s\right)M\omega \left(s\right)\text{d}s}\ge \frac{1}{b-a}{\left({\displaystyle {\int }_a^b\omega \left(s\right)\text{d}s}\right)}^{\text{T}}M\left({\displaystyle {\int }_a^b\omega \left(s\right)\text{d}s}\right)$

4. 主要结果

在本节中，将得到系统椭球形态且与时滞相关的可达集边界条件。

定理1 若存在对称矩阵 $P_{11},P_{21},P_{22},P_{31},P_{32},P_{33}>0$，适当维、数的矩阵 $R>0$, $Q>0$, $T>0$ 和 $\alpha >0$，满足不等式

$\Phi =\left[\begin{array}{cccccc}{\varphi }_{11}& {\varphi }_{12}& {\varphi }_{13}& {\varphi }_{14}& {\varphi }_{15}& {\varphi }_{16}\\ \ast & {\varphi }_{22}& {\varphi }_{23}& {\varphi }_{24}& {\varphi }_{25}& {\varphi }_{26}\\ \ast & \ast & {\varphi }_{33}& 0& 0& {\varphi }_{36}\\ \ast & \ast & \ast & {\varphi }_{44}& 0& 0\\ \ast & \ast & \ast & \ast & {\varphi }_{55}& 0\\ \ast & \ast & \ast & \ast & \ast & {\varphi }_{66}\end{array}\right]<0$ (9)

$P_{i11}-W_{i11}\le 0,i\in U_{uk},i\ne j,$ (10)

$P_{i11}-W_{i11}\le 0,i\in U_{uk},i=j,$ (11)

其中

${\varphi }_{11}=\alpha P_{i11}+P_{i21}^{\text{T}}{A}_i+A_i^{\text{T}}{P}_{i21}+P_{i31}^{\text{T}}+P_{i31}+hQ+{\displaystyle \underset{j\in u_k}{\overset{N}{\sum }}{\lambda }_{ij}\left(h\right)}\left(P_{j11}-W_{j11}\right),$

${\varphi }_{12}=P_{i11}^{\text{T}}+P_{i22}^{\text{T}}{A}_i+P_{i32}^{\text{T}}-P_{i21}^{\text{T}},$

${\varphi }_{13}=P_{i21}^{\text{T}}{B}_i+P_{i33}^{\text{T}}-P_{i31}^{\text{T}},{\varphi }_{14}=P_{i21}^{\text{T}}{C}_i\text{,}{\varphi }_{15}=P_{i21}^{\text{T}}{D}_i\text{,}{\varphi }_{16}=-P_{i31}^{\text{T}}\text{,}$

${\varphi }_{22}=-P_{i22}^{\text{T}}-P_{i22}+h^{2}S+\tau R,$

${\varphi }_{23}=P_{i22}^{\text{T}}{B}_i-P_{i32}^{\text{T}},{\varphi }_{24}=P_{i22}^{\text{T}}{C}_i\text{,}{\varphi }_{25}=P_{i22}^{\text{T}}{D}_i\text{,}{\varphi }_{26}=-P_{i32}^{\text{T}}\text{,}$

${\varphi }_{33}=-P_{i33}^{\text{T}}-P_{i33}-\left(1-h_d\right)h{\text{e}}^{-\alpha h}Q\text{,}{\varphi }_{36}=-P_{i33}^{\text{T}},$

${\varphi }_{44}=-\left(1-{\tau }_d\right)\tau {\text{e}}^{-\alpha \tau }R\text{,}{\varphi }_{55}=-\frac{\alpha }{{\omega }_m^2}I,{\varphi }_{66}=-{\text{e}}^{-ah}S,$

则系统(1)是稳定的。

证明：构造李雅普诺夫函数

$V\left(t,x_t\right)={\displaystyle \underset{i=1}{\overset{4}{\sum }}{V}_i\left(t,x_t\right),}$ (12)

其中

$V_1=x^{\text{T}}\left(t\right)P_{i11}{x}^{\text{T}}\left(t\right)={\eta }^{\text{T}}\left(t\right)\left[\begin{array}{ccc}I& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{ccc}{P}_{i11}& 0& 0\\ P_{i21}& P_{i22}& 0\\ P_{i31}& P_{i32}& P_{i33}\end{array}\right]\eta \left(t\right),$

其中 ${\eta }^{\text{T}}\left(t\right)=\left[\begin{array}{ccc}{x}^{\text{T}}\left(t\right)& {\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)& x^{\text{T}}\left(t-h\left(t\right)\right)\end{array}\right]$，

$V_2=\tau {\displaystyle {\int }_{t-\tau \left(t\right)}^t{\text{e}}^{a\left(s-t\right)}}{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)R\stackrel{\dot{}}{x}\left(s\right)\text{d}s,$

$V_3=h{\displaystyle {\int }_{t-h\left(t\right)}^t{\text{e}}^{a\left(s-t\right)}}{x}^{\text{T}}\left(s\right)Qx\left(s\right)\text{d}s,$

$V_4=h{\displaystyle {\int }_{-h\left(t\right)}^0{\displaystyle {\int }_{t+\theta }^t{\text{e}}^{a\left(s-t\right)}{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)S\stackrel{\dot{}}{x}\left(s\right)\text{d}s}},$

这里 $t-h\le s\le t$， $0<{\text{e}}^{-\alpha h}<{\text{e}}^{\alpha \left(s-t\right)}<1$。

取沿系统(1)对 $V\left(t,x_t\right)$ 求伊藤算子，根据引理1，可得

$\begin{array}{c}L{V}_1\left(t,x\left(t\right)\right)=\underset{\Delta \to 0}{\lim }\frac{\left[V\left(\eta \left(t+\Delta \right),r_{t+\Delta }\right)|\eta \left(t\right),r_t\right]-V\left(\eta \left(t\right),r_t\right)}{\Delta }\\ =\underset{\Delta \to 0}{\lim }\{{\displaystyle {\sum }_{j=1,j\ne i}^N\mathrm{Pr}\left\{r_{t+\Delta }=j|r_t=i\right\}{\eta }^{\text{T}}\left(t+\Delta \right)P_j\eta \left(t+\Delta \right)}\\ +\mathrm{Pr}\left\{r_{t+\Delta }=j|r_t=i\right\}{\eta }^{\text{T}}\left(t+\Delta \right)P_j\eta \left(t+\Delta \right)-{\eta }^{\text{T}}\left(t\right)P_j\eta \left(t\right)\}\end{array}$

根据模式i中驻留时间分布的无记忆性质，使用条件概率公式可得

$\begin{array}{c}L{V}_1\left(t,x\left(t\right)\right)=\underset{\Delta \to 0}{\lim }\frac{1}{\Delta }\{{\displaystyle {\sum }_{j=1,j\ne i}^N\frac{{\lambda }_{ij}\left(G_i\left(h+\Delta \right)-G_i\left(h\right)\right)}{1-G_i\left(h\right)}}{\eta }^{\text{T}}\left(t+\Delta \right)P_j\eta \left(t+\Delta \right)\\ +\frac{1-G_i\left(h+\Delta \right)}{1-G_i\left(h\right)}{\eta }^{\text{T}}\left(t+\Delta \right)P_j\eta \left(t+\Delta \right)-{\eta }^{\text{T}}\left(t\right)P_j\eta \left(t\right)\}\\ =\underset{\Delta \to 0}{\lim }\{{\displaystyle {\sum }_{j=1,j\ne i}^N\frac{{\lambda }_{ij}\left(G_i\left(h+\Delta \right)-G_i\left(h\right)\right)}{1-G_i\left(h\right)}}{\eta }^{\text{T}}\left(t+\Delta \right)P_j\eta \left(t+\Delta \right)\\ +\frac{1-G_i\left(h+\Delta \right)}{1-G_i\left(h\right)}{\eta }^{\text{T}}\left(t+\Delta \right)P_j\eta \left(t+\Delta \right)-\frac{1-G_i\left(h+\Delta \right)}{1-G_i\left(h\right)}{\eta }^{\text{T}}\left(t\right)P_j\eta \left(t+\Delta \right)\\ +\frac{1-G_i\left(h+\Delta \right)}{1-G_i\left(h\right)}{\eta }^{\text{T}}\left(t\right)P_j\eta \left(t+\Delta \right)-\frac{1-G_i\left(h+\Delta \right)}{1-G_i\left(h\right)}{\eta }^{\text{T}}\left(t\right)P_j\eta \left(t\right)\\ -\frac{G_i\left(h+\Delta \right)-G_i\left(h\right)}{1-G_i\left(h\right)}{\eta }^{\text{T}}\left(t\right)P_j\eta \left(t\right)\}\end{array}$

其中 $G_i\left(t\right)$ 是系统在模式i时驻留时间的累积分布函数。利用积累分布函数的性质，可得

$\underset{\Delta \to 0}{\lim }\frac{G_i\left(h+\Delta \right)-G_i\left(h\right)}{\left(1-G_i\left(h\right)\right)\Delta }={\lambda }_i\left(h\right),\underset{\Delta \to 0}{\lim }\frac{G_i\left(h+\Delta \right)-G_i\left(h\right)}{\left(1-G_i\left(h\right)\right)}=0,\underset{\Delta \to 0}{\lim }\frac{1-G_i\left(h+\Delta \right)}{1-G_i\left(h\right)}=1,$

因此，可以得到，

$\begin{array}{c}L{V}_1\left(t,x\left(t\right)\right)={\eta }^{\text{T}}\left(t\right){\displaystyle {\sum }_{j=1,j\ne i}^N{\lambda }_{ij}{\lambda }_i\left(h\right)P_j\eta \left(t\right)}+2{\eta }^{\text{T}}\left(t\right)P_j\stackrel{\dot{}}{\eta }\left(t\right)-{\lambda }_i\left(h\right){\eta }^{\text{T}}\left(t\right)P_j\eta \left(t\right)\\ =2{\eta }^{\text{T}}\left(t\right)P_j\stackrel{\dot{}}{\eta }\left(t\right)+{\eta }^{\text{T}}\left(t\right)\left({\displaystyle {\sum }_{j=1,j\ne i}^N{\lambda }_{ij}\left(h\right)P_j}\right)\eta (\; t\; )\end{array}$

即

$\begin{array}{c}L{V}_1=x^{\text{T}}\left(t\right)\left({\displaystyle \underset{i=1}{\overset{N}{\sum }}{\lambda }_{ij}\left(h\right)P_j}\right)x^{\text{T}}\left(t\right)+2{\eta }^{\text{T}}\left(t\right)\left[\begin{array}{ccc}{P}_{i11}^{\text{T}}& P_{i21}^{\text{T}}& P_{i31}^{\text{T}}\\ 0& P_{i22}^{\text{T}}& P_{i32}^{\text{T}}\\ 0& 0& P_{i33}^{\text{T}}\end{array}\right]\\ \times \left[\begin{array}{c}\stackrel{\dot{}}{x}\left(t\right)\\ A_{i}x\left(t\right)-\stackrel{\dot{}}{x}\left(t\right)+B_{i}x\left(t-h\left(t\right)\right)+C_{i}x\left(t-h\left(t\right)\right)+D_i\omega \left(t\right)\\ x\left(t\right)-x\left(t-h\left(t\right)\right)-{\displaystyle {\int }_{t-h\left(t\right)}^t\stackrel{\dot{}}{x}\left(s\right)\text{d}s}\end{array}\right]\end{array}$ (13)

考虑到转移概率是部分未知的情况，且 ${\displaystyle {\sum }_{j=1}^N{\lambda }_{ij}\left(h\right)=0}$，则当 $W_i=W_i^{\text{T}}$ 时

$-x^{\text{T}}\left(t\right)\left({\displaystyle \underset{i=1}{\overset{N}{\sum }}{\lambda }_{ij}\left(h\right)W_j}\right)x^{\text{T}}\left(t\right)=0,$ (14)

可得

$\begin{array}{c}L{V}_1\left(t,x_t\right)=x^{\text{T}}\left(t\right)\left[P_{i21}^{\text{T}}{A}_i+A_i^{\text{T}}{P}_{i21}+P_{i31}^{\text{T}}A+A^{\text{T}}{P}_{i31}\right]x\left(t\right)\\ +2x^{\text{T}}\left(t\right)\left[P_{i11}^{\text{T}}+P_{i22}^{\text{T}}{A}_i+P_{i32}^{\text{T}}-P_{i21}^{\text{T}}\right]\stackrel{\dot{}}{x}\left(t\right)\\ +2x^{\text{T}}\left(t\right)\left[P_{i21}^{\text{T}}{B}_i+P_{i33}^{\text{T}}-P_{i31}^{\text{T}}\right]x^{\text{T}}\left(t-h\left(t\right)\right)+2x^{\text{T}}\left(t\right)\left[P_{i21}^{\text{T}}{D}_i\right]\omega \left(t\right)\\ +2x^{\text{T}}\left(t\right)\left[P_{i21}^{\text{T}}{C}_i\right]\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)+2x^{\text{T}}\left(t\right)\left[P_{i31}^{\text{T}}\right]{\displaystyle {\int }_{t-h\left(t\right)}^t\stackrel{\dot{}}{x}\left(s\right)\text{d}s}\end{array}$

$\begin{array}{l}+{\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)\left[-P_{i22}-P_{i22}^{\text{T}}\right]\stackrel{\dot{}}{x}\left(t\right)+2{\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)\left[P_{i22}^{\text{T}}{C}_i\right]\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)\\ +2{\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)\left[P_{i22}^{\text{T}}{B}_i-P_{i32}^{\text{T}}\right]x\left(t-h\left(t\right)\right)+2{\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)\left[P_{i22}^{\text{T}}{D}_i\right]\omega \left(t\right)\\ +2{\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)\left[P_{i32}^{\text{T}}\right]{\displaystyle {\int }_{t-h\left(t\right)}^t\stackrel{\dot{}}{x}\left(s\right)\text{d}s}+x^{\text{T}}\left(t-h\left(t\right)\right)\left[-P_{i33}^{\text{T}}-P_{i31}^{\text{T}}\right]x\left(t-h\left(t\right)\right)\\ +2x^{\text{T}}\left(t-h\left(t\right)\right)\left[-P_{i32}^{\text{T}}\right]{\displaystyle {\int }_{t-h\left(t\right)}^t\stackrel{\dot{}}{x}\left(s\right)\text{d}s}+x^{\text{T}}\left(t\right){\displaystyle \underset{j\in u_k}{\overset{N}{\sum }}{\lambda }_{ij}\left(h\right)}\left(P_j-W_j\right)x\left(t\right)\end{array}$ (15)

$\begin{array}{c}L{V}_2\left(t,x_t\right)={\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)\tau R\stackrel{\dot{}}{x}\left(t\right)-\left(1-\stackrel{\dot{}}{\tau }\left(t\right)\right){\text{e}}^{-\alpha \tau }{\stackrel{\dot{}}{x}}^{\text{T}}\left(t-\tau \left(t\right)\right)\tau R\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)-\alpha V_2\\ \le {\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)\left(\tau R\right)\stackrel{\dot{}}{x}\left(t\right)-\left(1-{\tau }_d\right){\text{e}}^{-\alpha \tau }{\stackrel{\dot{}}{x}}^{\text{T}}\left(t-\tau \left(t\right)\right)\left(\tau R\right)\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)-\alpha V_2\end{array}$ (16)

$\begin{array}{c}L{V}_3\left(t,x_t\right)=x^{\text{T}}\left(t\right)\left(hQ\right)x\left(t\right)-\left(1-\stackrel{\dot{}}{h}\left(t\right)\right)x^{\text{T}}\left(t-h\left(t\right)\right)\left(hQ\right)x\left(t-h\left(t\right)\right)-\alpha V_3\\ \le x^{\text{T}}\left(t\right)\left(hQ\right)x\left(t\right)-\left(1-h_d\right){\text{e}}^{-\alpha h}{x}^{\text{T}}\left(t-h\left(t\right)\right)\left(hQ\right)x\left(t-h\left(t\right)\right)-\alpha V_3\end{array}$ (17)

$\begin{array}{c}L{V}_4\left(t,x_t\right)={\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)\left(hh\left(t\right)S\right)\stackrel{\dot{}}{x}\left(t\right)-h{\text{e}}^{-\alpha h}{\displaystyle {\int }_{t-h\left(t\right)}^t{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)S\stackrel{\dot{}}{x}\left(s\right)\text{d}s}-\alpha V_4\\ \le {\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)\left(h^{2}S\right)\stackrel{\dot{}}{x}\left(t\right)-h{\text{e}}^{-\alpha h}{\displaystyle {\int }_{t-h\left(t\right)}^t{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)S\stackrel{\dot{}}{x}\left(s\right)\text{d}s}-\alpha V_4\end{array}$ (18)

根据引理3，

$\begin{array}{c}-h{\text{e}}^{-\alpha h}{\displaystyle {\int }_{t-h\left(t\right)}^t{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)S\stackrel{\dot{}}{x}\left(s\right)\text{d}s}\le -\frac{h}{h\left(t\right)}{\text{e}}^{-\alpha h}{\left({\displaystyle {\int }_{t-h\left(t\right)}^t\stackrel{\dot{}}{x}\left(s\right)\text{d}s}\right)}^{\text{T}}S\left({\displaystyle {\int }_{t-h\left(t\right)}^t\stackrel{\dot{}}{x}\left(s\right)\text{d}s}\right)\\ \le -{\text{e}}^{-\alpha h}{\left({\displaystyle {\int }_{t-h\left(t\right)}^t\stackrel{\dot{}}{x}\left(s\right)\text{d}s}\right)}^{\text{T}}S\left({\displaystyle {\int }_{t-h\left(t\right)}^t\stackrel{\dot{}}{x}\left(s\right)\text{d}s}\right)\end{array}$ (19)

故有

$L{V}_4\left(t,x_t\right)\le -\alpha V_4+{\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)\left(h^{2}S\right)\stackrel{\dot{}}{x}\left(t\right)-{\text{e}}^{-\alpha h}{\left({\displaystyle {\int }_{t-h\left(t\right)}^t{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)\text{d}s}\right)}^{\text{T}}S\left({\displaystyle {\int }_{t-h\left(t\right)}^t{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)\text{d}s}\right).$ (20)

综合(9)~(20)可得

$LV\left(t,x_t\right)+\alpha V\left(t,x_t\right)-\frac{\alpha }{{\omega }_m^2}{\omega }^{\text{T}}\left(t\right)\omega \left(t\right)\le {\xi }^{\text{T}}\left(t\right)\Phi \xi \left(t\right)+x^{\text{T}}\left(t\right){\displaystyle \underset{j\in u_k}{\overset{N}{\sum }}{\lambda }_{ij}\left(h\right)}\left(P_{j11}-W_{j11}\right)x\left(t\right)<0,$

其中 ${\xi }^{\text{T}}\left(t\right)=\left[x\left(t\right)\stackrel{\dot{}}{x}\left(t\right)x^{\text{T}}\left(t-h\left(t\right)\right){\stackrel{\dot{}}{x}}^{\text{T}}\left(t-\tau \left(t\right)\right)w\left(t\right){\displaystyle {\int }_{t-h\left(t\right)}^t{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)\text{d}s}\right]$。

根据引理1，可知 $V\left(t,x_t\right)\le 1$，而由于 $V_1\left(t,x_t\right)+V_2\left(t,x_t\right)+V_3\left(t,x_t\right)+V_4\left(t,x_t\right)\ge 0$，则

$V_1\left(t,x_t\right)\le 1$。

因此，系统(1)的可达集由(7)中定义的椭球 $\Im \left(P\right)$ 约束边界，这意味在(2)和(3)的约束下，系统(1)的可达集由非椭球边界表示。所以，定理1得证。

当系统(1)中 $\tau \left(t\right)=\tau ,h\left(t\right)=h$ 时，系统(1)则为

$\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)-C_{\left(t,r_t\right)}\stackrel{\dot{}}{x}\left(t-\tau \right)=A_{\left(t,r_t\right)}x\left(t\right)+B_{\left(t,r_t\right)}x\left(t-h\right)+D_{\left(t,r_t\right)}\omega \left(t\right),\\ x\left(t_0+\theta \right)\equiv 0,\forall t\in \left[-h,0\right].\end{array}$ (21)

使用与定理1相同的方法研究系统(2)，得到系统(2)的可达集边界判定条件。

定理2若存在对称矩阵 $P_{11},P_{21},P_{22},P_{31},P_{32},P_{33}>0$，适当维数的矩阵 $R>0$, $Q>0$, $T>0$ 和 $\alpha >0$，满足不等式

$\Phi =\left[\begin{array}{cccccc}{\varphi }_{11}& {\varphi }_{12}& {\varphi }_{13}& {\varphi }_{14}& {\varphi }_{15}& {\varphi }_{16}\\ \ast & {\varphi }_{22}& {\varphi }_{23}& {\varphi }_{24}& {\varphi }_{25}& {\varphi }_{26}\\ \ast & \ast & {\varphi }_{33}& 0& 0& {\varphi }_{36}\\ \ast & \ast & \ast & {\varphi }_{44}& 0& 0\\ \ast & \ast & \ast & \ast & {\varphi }_{55}& 0\\ \ast & \ast & \ast & \ast & \ast & {\varphi }_{66}\end{array}\right]<0$ (22)

$P_{i11}-W_{i11}\le 0,i\in U_{uk},i\ne j,$ (23)

$P_{i11}-W_{i11}\le 0,i\in U_{uk},i=j,$ (24)

其中

${\varphi }_{11}=\alpha P_{i11}+P_{i21}^{\text{T}}{A}_i+A_i^{\text{T}}{P}_{i21}+P_{i31}^{\text{T}}+P_{i31}+hQ+{\displaystyle \underset{j\in u_k}{\overset{N}{\sum }}{\lambda }_{ij}}\left(P_{j11}-W_{j11}\right),$

${\varphi }_{12}=P_{i11}^{\text{T}}+P_{i22}^{\text{T}}{A}_i+P_{i32}^{\text{T}}-P_{i21}^{\text{T}},$

${\varphi }_{13}=P_{i21}^{\text{T}}{B}_i+P_{i33}^{\text{T}}-P_{i31}^{\text{T}},{\varphi }_{14}=P_{i21}^{\text{T}}{C}_i\text{,}{\varphi }_{15}=P_{i21}^{\text{T}}{D}_i\text{,}{\varphi }_{16}=-P_{i31}^{\text{T}}\text{,}$

${\varphi }_{22}=-P_{i22}^{\text{T}}-P_{i22}+h^{2}S+\tau R,{\varphi }_{23}=P_{i22}^{\text{T}}{B}_i-P_{i32}^{\text{T}},{\varphi }_{24}=P_{i22}^{\text{T}}{C}_i\text{,}$

${\varphi }_{25}=P_{i22}^{\text{T}}{D}_i\text{,}{\varphi }_{26}=-P_{i32}^{\text{T}}\text{,}$

${\varphi }_{33}=-P_{i33}^{\text{T}}-P_{i33}-h{\text{e}}^{-\alpha h}Q\text{,}{\varphi }_{36}=-P_{i33}^{\text{T}},$

${\varphi }_{44}=-\tau {\text{e}}^{-\alpha \tau }R\text{,}{\varphi }_{55}=-\frac{\alpha }{{\omega }_m^2}I,{\varphi }_{66}=-{\text{e}}^{-ah}S,$

则系统(2)稳定。由于证明过程与定理1相似，因此此处省略。

注 4.1实际上，如果所有的转换概率都是未知的，相应的系统可以看作是任意切换状态下的中立型半马尔科夫跳跃系统。因此，定理1中得到的条件将涵盖任意切换状态下具有扰动的结果。在这种情况下，对于许多约束，定理1中可达集的边界变得非常保守。然而，在所有中立型半马尔科夫跳跃概率未知的情况下，我们可以利用李雅普诺夫泛函方法分析中立型半马尔科夫跳跃系统的可达集的边界。

注 4.2如果定理1中矩阵不等式的解存在，则不一定是唯一的。由于 $\det {\left(P_{1i}\right)}^{1/2}$ 的值最小时，椭球 $\Im \left(P_{i11}\right)$ 的体积也是最小，所以往往用 $\det {\left(P_{1i}\right)}^{1/2}$ 来衡量 $\Im \left(P_{i11}\right)$ 的体积。然而，寻求 $\det {\left(P_{1i}\right)}^{1/2}$ 的值较为困难，通常以 $I{\delta }_i\le P_{i11}$ 中 ${\delta }_i$ 的最大值来表示 $\det {\left(P_{1i}\right)}^{1/2}$ 的最小值，即

$\begin{array}{l}\text{minimize}\bar{\delta }\left(\bar{\delta }=\frac{1}{\delta }\right)\\ \text{s}\text{.t}\text{.}\{\begin{array}{l}\left(a\right)\left[\begin{array}{l}\bar{\delta }II\\ I{P}_{i11}\end{array}\right],i\in \zeta \\ \left(b\right)满足\left(9-11\right)或者\left(22\text{-}24\right)\end{array}\end{array}$ (25)

注 4.3由于定理1的矩阵不等式均只含有一个非凸的变量a > 0，所以当a为标量时，(9)和(22)为线性不等式。这样可以通过Matlab找到一个局部最优值a，使得矩阵不等式有可行解。

5. 数值算例

本节的数值示例证明了该方法的有效性，系统及状态矩阵如下

例1. $\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)-C_{\left(t,r_t\right)}\stackrel{\dot{}}{x}\left(t-0.01\right)=A_{\left(t,r_t\right)}x\left(t\right)+B_{\left(t,r_t\right)}x\left(t-0.01\right)+D_{\left(t,r_t\right)}\omega \left(t\right),\\ x\left(t_0+\theta \right)=\phi \left(\theta \right),\forall \theta \in \left[-h,0\right],\end{array}$ (26)

$\begin{array}{l}{A}_1=\left[\begin{array}{cc}-2& -1\\ 0& -2\end{array}\right],B_1=\left[\begin{array}{cc}-1& 0\\ -1& -2\end{array}\right],C_1=\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right],D_1=\left[\begin{array}{c}-0.15\\ 0.15\end{array}\right],\\ A_2=\left[\begin{array}{cc}-3& 0\\ 0& -2\end{array}\right],B_2=\left[\begin{array}{cc}-2& 0\\ -1& -1\end{array}\right],C_2=\left[\begin{array}{cc}-0.1& 0\\ 0& -0.1\end{array}\right],D_2=\left[\begin{array}{c}-0.14\\ 0.35\end{array}\right],\\ A_3=\left[\begin{array}{cc}-2& 0\\ -1& -1.5\end{array}\right],B_3=\left[\begin{array}{cc}-2& 0\\ 0& -2\end{array}\right],C_3=\left[\begin{array}{cc}0.15& 0\\ 0& 0.15\end{array}\right],D_3=\left[\begin{array}{c}-0.2\\ 0.3\end{array}\right],\end{array}$

考虑以下三种转移率矩阵，

情况1 所有转移概率已知

$\Lambda =\left[\begin{array}{ccc}-0.6& 0.2& 0.4\\ 0.6& -1& 0.4\\ 0.3& 0.5& -0.8\end{array}\right]$

情况2 部分转移概率已知

$\Lambda =\left[\begin{array}{ccc}-0.6& 0.2& 0.4\\ ?& ?& ?\\ ?& ?& ?\end{array}\right]$

情况3 所有转移概率未知

$\Lambda =\left[\begin{array}{ccc}?& ?& ?\\ ?& ?& ?\\ ?& ?& ?\end{array}\right]$

通过给出不同过渡概率Λ，得出中立型半马尔科夫跳跃系统(1)的模态演化(见图1)。基于图1所示的模态演变，选择干扰 $\omega \left(t\right)$ 作为满足 ${\omega }^{\text{T}}\left(t\right)\omega \left(t\right)\le 1$ 的随机信号，从原点开始的满足系统(1)的所有可达状态(见图2)。进一步得到了系统(1)的状态轨迹及其可达集的椭球形边界(见图3)。

Figure 1. Modal switching diagram of system (1)

图1. 系统(1)的模态切换图

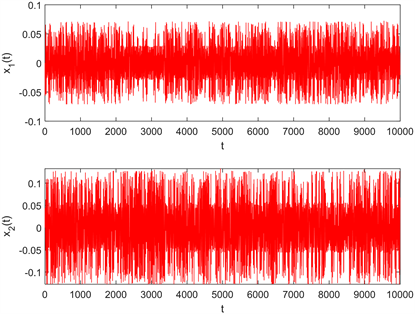
Figure 2. The time responses of state variable x(t) of neutral semi-markov jump system (1)

图2. 中立型半马科夫跳跃系统(1)状态变量x(t)的时间响应图

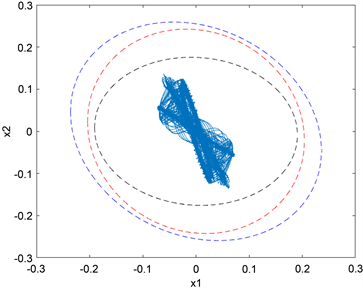
Figure 3. Status track of neutral semi-markov jump system (1)

图3. 中立型半马科夫跳跃系统(1)的状态轨迹图

Figure 4. The bound of reachable set for neutral semi-markov jump system (1) in case 1

图4. 条件1的中立型半马科夫跳跃系统(1)可达集的边界

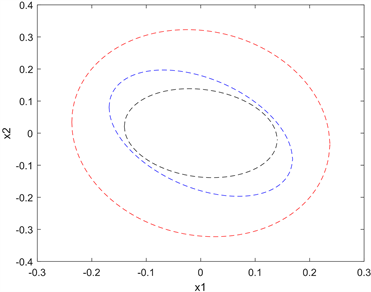
Figure 5. The bound of reachable set for neutral semi-markov jump system (1) in case 2

图5. 条件2的中立型半马科夫跳跃系统(1)可达集的边界

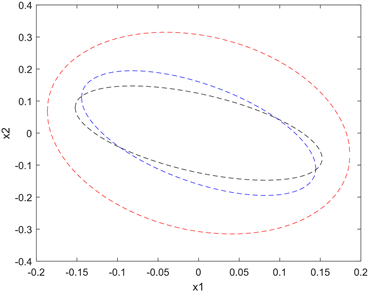
Figure 6. The bound of reachable set for neutral semi-markov jump system (1) in case 3

图6. 条件3的中立型半马科夫跳跃系统(1)可达集的边界

在条件1状态下， $\alpha =0.1$，得到一个较小的可达集的椭球边界(见图4) $\det {\left(P_{1i}\right)}^{1/2}$ 的最小值 $\bar{\delta }=0.1510$，相对应的矩阵：

$P_1=\left[\begin{array}{cc}34.3677& 6.1525\\ 6.1525& 21.6707\end{array}\right],P_2=\left[\begin{array}{cc}68.6858& 20.5980\\ 20.2980& 60.2248\end{array}\right],P_3=\left[\begin{array}{cc}38.6983& 4.4880\\ 4.4880& 43.0517\end{array}\right].$

在条件2状态下， $\alpha =0.1$，得到可达集(见图5)的椭球边界 $\det {\left(P_{1i}\right)}^{1/2}$ 的最小值 $\bar{\delta }=0.2017$，相对应的矩阵：

$P_1=\left[\begin{array}{cc}50.6476& 7.4672\\ 7.4672& 51.8182\end{array}\right],P_2=\left[\begin{array}{cc}17.2620& 1.3054\\ 1.3054& 9.1745\end{array}\right],P_3=\left[\begin{array}{cc}41.2156& 14.1638\\ 14.1638& 30.2139\end{array}\right].$

在条件3状态下， $\alpha =0.1$，得到一个较小的可达集的椭球边界(见图6)，其 $\det {\left(P_{1i}\right)}^{1/2}$ 的最小值 $\bar{\delta }=0.1315$，相对应的矩阵：

$P_1=\left[\begin{array}{cc}59.6393& 31.8783\\ 31.8783& 63.9863\end{array}\right],P_2=\left[\begin{array}{cc}28.8902& 3.5118\\ 3.5118& 10.5077\end{array}\right],P_3=\left[\begin{array}{cc}68.9398& 28.2411\\ 28.2411& 28.6880\end{array}\right].$

6. 总结

本文研究了具有实变时滞的中立型半马尔科夫跳跃系统的可达集边界问题，通过构造李雅普诺夫函数，结合线性矩阵不等式方法，得到了满足可达集的判定条件。使用Matlab的LMI工具包结合数值算例对该结果进行计算，根据不同的过度概率矩阵得到了相对应的表示椭圆体积的最小值，且得到了一个较小的椭球边界。由此，证明了该方法的可行性和有效性。

基金项目

贵州省科技厅科学研究基金(ZK[2021]016)。

NOTES

^*通讯作者。