1. 引言
目前,“碳达峰、碳中和”得到了社会各行业的广泛关注。为了实现“十四五”期间建筑行业全面二氧化碳排放量达峰,需要整个行业共同努力。再生混凝土可以将部分建筑垃圾转化为混凝土的粗细骨料,减少固体废弃物排放,节约资源和能源。因此,发展再生混凝土技术已经得到全行业的重点关注。目前对再生混凝土在复杂应力状态下的力学特性研究较为缺乏。
单轴压缩试验是研究混凝土力学性质最基本的试验,但试验结果受试件的尺寸、形状、加载速率、试件与加载垫板之间的摩擦等影响。其中,端部摩擦会使试件与加载垫板端部之间产生剪应力,从而影响混凝土的力学性能,许多学者对此进行了研究。尤明庆和苏承东 [1] 通过试验发现,将聚四氟乙烯垫片垫在试件与加载端部之间会使大理岩的单轴抗压强度降低。梁正召等 [2] 采用RFPA3D对不同形状岩石在不同端部条件下进行了单轴压缩数值试验。Indelicato F.和Paggi M. [3] 采用有限元分析了不同形状混凝土试件的抗压强度。陈健云等 [4] 采用复合型界面损伤本构模型,进行了数值模拟并分析了单轴压缩试验中不同端部条件对试件变形以及破坏过程的影响。康政等 [5] 利用PFC3D数值模拟了端部摩擦下混凝土标准立方体和标准圆柱体试件的单轴抗压强度和破裂形态特征。金浏等 [6] 选取不同的端部摩擦因数,模拟了中低应变率下的混凝土动态压缩数值试验,分析了端部摩擦因数对动态抗压强度的影响。
由于端部摩擦的存在,在进行试验时,试件与加载垫板之间会产生不同于试件和垫板的力学响应,出现非连续变化现象,按实体结构建立的理论难以分析接触面的力学行为 [7]。对此,本文基于基面力单元法,建立了二维再生混凝土随机骨料细观模型,并引入零厚度界面单元 [8] 模拟试件与加载面之间的摩擦行为,讨论了单轴压缩试验中端部摩擦对再生混凝土试件的峰值强度和破坏模式的影响。
2. 细观模型简介
2.1. 随机骨料生成及网格划分
再生混凝土可视为由天然骨料、老砂浆、天然骨料与老砂浆之间的粘结界面、新砂浆、老砂浆与新砂浆之间的粘结界面组成的五相复合材料。本文骨料假定骨料为球形,参考Walraven公式 [9],利用蒙特卡罗法,建立了随机骨料模型。网格剖分方面,使用Matlab编程,对再生混凝土骨料内外分别布点,采用了与粘结界面对齐的Delaunay三角形剖分,图1为骨料分布及网格剖分示意图。
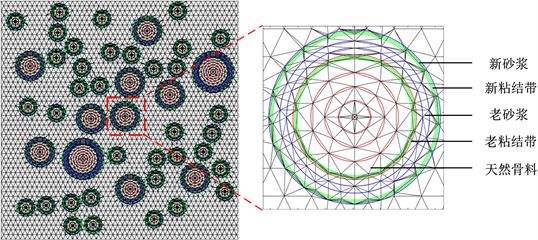
Figure 1. Schematic diagram of random aggregate distribution and meshing of recycled aggregate concrete
图1. 再生混凝土随机骨料分布及网格剖分示意图
2.2. 基面力单元法的单元刚度矩阵
基于Gao [10] 提出的基面力的概念,Peng等 [11] [12] 提出了基面力单元法(BFEM),并推导得到一个三角形单元(如图2)刚度矩阵中任意元素
的表达式如下
(1)
式中,E表示杨氏模量,A表示单元面积,
表示泊松比,
表示单位张量,
,
,其中
(2)
式中,
表示径矢,
为
的共轭向量。
2.3. 零厚度界面单元 [8] 基本原理
零厚度界面单元在建立了应力–节点位移关系的同时,还考虑了结构与接触面之间的单元不连续性,它可以考虑切向与法向的刚度系数,因此能够模拟再生混凝土试件与加载垫板间的摩擦行为。
图3表示一个零厚度界面单元,其长度为l,宽度e为零,坐标原点位于形心。
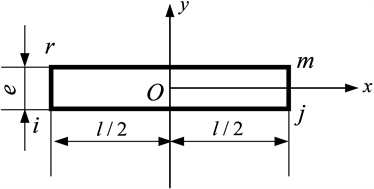
Figure 3. A zero-thickness interface element
图3. 一个零厚度界面单元
在局部坐标系中,零厚度界面单元的应力–节点位移关系为
(3)
式中,
表示切向剪应力,
表示法向正应力;令
(4)
式中,
和
分别表示单元上、下缘的水平位移差和垂直位移差;
表示切向刚度系数,
表示法向刚度系数。
结合文献 [13] 得到零厚度界面单元的单元刚度矩阵如下
(5)
上式即为零厚度界面单元的单元刚度矩阵的表达式。
2.4. 损伤本构模型和强度准则
根据Lemaitre的应变等价原理 [14],损伤后材料的名义应力可用其有效应力在未损伤材料中的应变表示:
(6)
若泊松比不受损伤所影响,损伤后的弹性模量可以用初始弹性模量来表示
(7)
式中,E0为初始弹性模量;E为损伤后的弹性模量;D为损伤因子。
许多学者已经得出再生混凝土在外荷载的作用下宏观应力–应变曲线之所以呈非线性,主要是由微裂缝的扩展引起。本文采用多折线损伤本构模型 [15] 进行计算,综合文献 [16] [17] [18] [19],选取再生混凝土的各相材料参数如表1。
(8)
(9)
式中,
为峰值应变;
为残余应变系数,
;
为极限应变系数,
;
为弹性应变系数,
;
为弹性抗压强度系数,
;
为残余抗压强度系数;
为残余抗拉强度系数;下标t和c代表抗拉和抗压两种状态。

Table 1. Mechanical parameters of each phase material of recycled concrete
表1. 再生混凝土各相材料的力学参数
在考虑端部摩擦的数值试件中,双压区采用Kupfer [20] 双轴强度破坏准则,不考虑端部摩擦的数值试件直接采用最大拉应变准则。Kupfer双轴强度破坏准则表达式为:
(10)
式中:拉应力为正,
为双轴抗压强度,
,
为双轴受压时最小主应力与最大主应力之比;
为混凝土单轴受压极限强度。
3. 模拟方案
对100 mm × 100 mm、100 mm × 150 mm和100 mm × 200 mm三种尺寸的试件分别进行两种模拟方案,即不考虑试件与加载垫板之间的端部摩擦与考虑端部摩擦,对应的数值计算模型分别如图4(a),图4(b)。其中上下加载垫板厚20 mm,采用逐级静态位移加载,加载位移增量
,在加载垫板和试件接触面上设置零厚度界面单元。为防止零厚度界面单元两侧法向单元相互嵌入,法向刚度系数需设一较大值,结合文献 [21],可选取法向刚度
。切向刚度系数
取值越大,代表试件与垫板之间的摩擦越大,结合文献 [13] [22],取
以模拟端部摩擦存在的情况。
4. 计算结果与分析
4.1. 端部摩擦对再生混凝土试件峰值强度的影响
由表2可知,考虑试件与加载垫板之间的端部摩擦时,不同尺寸的再生混凝土试件的峰值强度较不考虑端部摩擦时均有升高。图5的曲线是根据每个尺寸对应的6个随机试件的峰值强度平均值绘制的,其中,高宽比为2时,提高6.73%,高宽比为1.5时,提高11.31%,高宽比为1时,端部摩擦的存在使试件的峰值强度提高23.02%,由此可以得出:与普通混凝土类似,端部摩擦的存在会使再生混凝土试件的峰值强度提高,随着高宽比的减小,提高的幅度呈上升趋势,这与Van Vliet [23] 的试验结论一致,对比情况见表3。

Table 2. Peak strength of recycled concrete specimen
表2. 再生混凝土试件的峰值强度
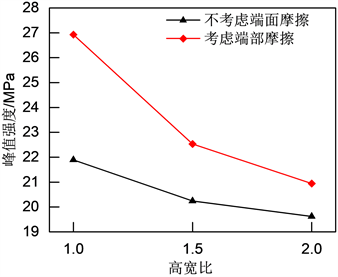
Figure 5. Peak strength of specimens with different slenderness under different end conditions
图5. 不同端部条件下不同高宽比试件的峰值强度

Table 3. Comparison between the simulation results and test result
表3. 计算结果与试验结果对比
4.2. 端部摩擦对再生混凝土试件破坏模式的影响
与普通混凝土相比,再生混凝土的破坏程度更严重 [24]。不考虑试件与加载垫板之间的端部摩擦时,再生混凝土试件破坏图如图6。端部的损伤较为严重;对于高宽比为1的试件,裂缝在试件中分布较为均匀,破裂方向与加载方向大致相同。高宽比增加,裂纹范围逐渐减小,破坏模式有所变化,宏观破裂带倾斜程度有所增加,引起局部剪切破坏,但端部都有较为严重的损伤。
考虑端部摩擦时,再生混凝土试件破坏图如图7,由于试件端部的侧向变形受到限制,阻碍了裂缝平行于加载方向发展,被迫沿斜向扩展。对于高宽比为1的试件,试件最终破坏模式为指向试件四角的X型劈裂,高宽比增大时,试件高度中部受端部摩擦影响较小,破坏较为严重,上下端部因为端部摩擦的存在而少有破坏。
4.3. 结果分析
当试件受到摩擦力和加载力的作用时,试件端部将处于双轴受压状态从而产生应力集中现象,根据圣维南原理,中部区域因远离端部将处于近似单轴受压状态(如图8)。因此,端部摩擦存在时,裂纹只能发生在侧向变形不受限制或受限制较为薄弱的部分,即试件必须在更高的外荷载水平下才能发生破坏,表现为峰值强度提高。高宽比越小,端部约束的影响范围所占整个试件的比例越大,所以高宽比较小时,峰值强度提高的幅度将增加。
 (a) 100 mm × 100 mm
(a) 100 mm × 100 mm  (b) 100 mm × 150 mm
(b) 100 mm × 150 mm  (c) 100 mm × 200 mm
(c) 100 mm × 200 mm
Figure 6. The final failure mode of the specimens without considering the end friction
图6. 不考虑端部摩擦时试件的最终破坏模式
 (a) 100 mm × 100 mm
(a) 100 mm × 100 mm  (b) 100 mm × 150 mm
(b) 100 mm × 150 mm  (c) 100 mm × 200 mm
(c) 100 mm × 200 mm
Figure 7. The final failure mode of the specimens considering the end friction
图7. 考虑端部摩擦时试件的最终破坏模式
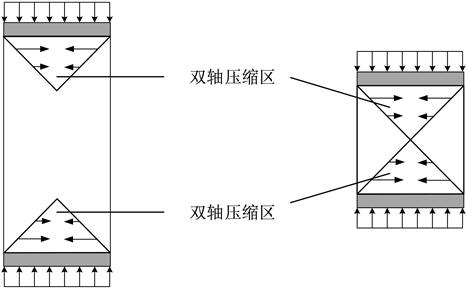
Figure 8. Biaxial compression zones of specimens
图8. 试件双轴压缩区
5. 结论
利用基面力单元法,本文引入零厚度界面单元考虑了再生混凝土试件与加载垫板之间的摩擦,讨论了单轴受压时端部摩擦对再生混凝土试件峰值强度和破坏模式的影响。结果表明:
1) 在基面力单元法中引入零厚度界面单元可较好的用于模拟再生混凝土试件与垫板之间的摩擦,且模拟结果与试验结果一致,证明了本文模型的可靠性。
2) 考虑试件与加载垫板之间的端部摩擦时,再生混凝土试件的高宽比对峰值强度的影响较不考虑端部摩擦时更明显。
3) 端部摩擦会显著影响再生混凝土试件的峰值强度和破坏模式,并且随着高宽比减小,影响程度增大。
端部摩擦的影响范围有限,距离端部越远,受到的影响越小。具体表现为:端部摩擦存在时,试件的高宽比越大,峰值强度的提高程度越小;在破坏模式方面,试件高度中部受端部摩擦影响较小,破坏较为严重,上下端部因为端部摩擦的存在而少有破坏。
基金项目
本文由国家自然科学基金项目(No.10972015, No.11172015),北京市自然科学基金项目(8162008)资助。
参考文献