1. 引言
实体解析(Entity Resolution)是数据清洗的重要部分,对于数据挖掘和数据集成也至关重要 [1] [2] [3] [4] [5]。在实践中,数据集成和数据挖掘常常涉及多个数据源,不同的数据提供方对同一个事物即实体(Entity)可能会有不同的描述。由于拼写错误、缩写方式不同、描述格式不同、属性值缺失、实体的某些属性值随着时间推移发生变化(比如年龄、居住地点、工作单位)等,描述同一实体的不同记录存在差异 [6]。实体解析是从一个或多个数据源中匹配描述同一现实世界实体记录的过程。为了实现高质量的数据集成和数据挖掘,需要对数据进行实体解析。凭借数十年的研究,传统的实体解析拥有高效且有效的算法解决方案 [7] [8] [9] [10]。但传统的实体解析仅针对单一类型的实体解析问题,匹配的记录之间是独立的。
大数据时代,数据呈现多样性和关联性,在实体解析中体现为数据集包含多个实体集,实体集之间具有关联关系,我们称为关联数据集。这种对关联数据集进行的实体解析,即关联实体解析(Relational Entity Resolution)。本文中,我们专注于对一对多关联实体进行实体解析。在关联实体解析中,关联数据集由多个实体集和它们之间的关系组成。在这种数据集中,某些实体的解析可能会影响到其他实体的解析。现有的关联实体解析 [11] [12] [13] [14] [15] [16] 中,很少有人专注于一对多关联实体的实体解析问题。比如Dong等人 [14] 通过关联关系将可能匹配的记录作为节点,构建依赖图来进行关联实体解析;Bhattacharya等人 [11] 利用引文数据中的共同作者关系,进行基于关系的聚类,来实现关联实体解析,这些关联实体解析方法都将实体间的关联关系假定为平等的,这类关联实体解析方法在一对多关联实体的实体解析上效果不是很理想。因此为了高效地解决一对多关联实体的实体解析问题,本文提出一种关联树模型,利用树的层次特性来描述关联实体之间的一对多关联关系。基于关联树模型,我们提出了一种关联树搜索算法,在树中高效有序地搜索相似匹配的节点对,并提出一种相似树索引来表示关联树的匹配结果,以便于后续的关联树合并与节点合并。传统的属性相似度算法无法发掘关联实体的关联关系进行实体解析,因此本文基于属性相似度提出一种关联实体匹配算法,将本节点的属性相似度和关联子节点的部分属性相似度结合起来判断节点是否匹配。本文的主要贡献如下:
1) 以集合划分为基础,基于基本的关联实体解析模型,提出基于一对多关联关系的关联树实体解析模型,并引申出相似节点、相似树、相似性传递等概念。
2) 为了查找相似的关联实体,本文提出一种关联树搜索算法,该算法基于一对多关联实体的相似性传递性质来进行深度优先搜索。为了表示关联树的匹配结果,便于后续的关联树合并,本文提出一种相似树索引,映射关联树中的相似节点。
3) 针对一对多关联实体解析问题,本文提出一种节点匹配算法,将本节点的属性相似度和关联子节点的部分属性相似度结合起来判断节点是否匹配。
4) 在房地产大数据的真实数据集上进行了充分的实验,实验结果表明本文提出的基于关联树模型的实体解析方法与现有的关联实体解析方法相比具有良好效果。
2. 关联树模型
2.1. 关联实体解析模型
实体类型指的是实体的关系模式类型,比如盘是一种实体类型而栋是另一种实体类型。每一个记录r都描述真实世界的一个实体,即都属于一个实体类型。由于数据常常源于多个数据源,因此记录集中可能存在多个记录描述同一真实世界的实体。记录包括多个属性,分为简单属性和引用属性两类:简单属性的值是字符串、整型、浮点型等简单类型;引用属性的值是对另外一个实体类型的记录的引用。图1(c)中,栋名是栋实体的简单属性;盘名是栋实体记录指向盘体的引用,是引用属性。
我们将数据集划分为由一个个簇组成的集合,每个簇都代表一个真实世界的实体。因此我们将簇c定义为一组记录。给定实体集
,实体集R即为簇集
,其中
,
且
,
。
传统实体解析算法解析单个实体集R。实体解析算法接收R的一个划分
作为输入,并返回R的另一个划分
。划分是表示实体解析算法输出的一种通用方法。比如当前只考虑图1(c)中的栋实体集
,B的实体解析问题就是对B的划分问题。输入的实体集B可以看作单个划分
,实体解析算法输出的为划分
。如果我们在R的一个划分
运行实体解析算法产生R的另一个划分
,这一过程称为传统实体解析 [17]。
关联实体解析不同于传统的实体解析,要对多类型的,关联的实体集同时进行实体解析,实体解析过程中要考虑不同类别的记录间的关联关系。接下来举例说明,图1(b)~(d)分别为房地产数据集种的三个实体集,图1(a)为三个实体集的关联关系,用ER图的形式表示,其中包括盘与栋之间的一对多关系,栋与户之间的一对多关系;在已知房地产数据集种各实体集的关联关系(图1(a))情况下,如何判断三种类型实体集的重复记录就是一个关联实体解析问题。关联实体解析利用实体间关联关系优化不同类型实体的实体解析顺序提高实体解析的效率。比如
和
匹配后,因为栋实体集B与户实体集H具有关联关系,则与
匹配的记录可能在
中,应该优先对这些实体子集进行匹配。
2.2. 关联树模型
现实世界的实体联系一般都可以转换为一对多的联系,而这种一对多实体的实例的对应关系可以表示为树结构,比如房地产领域的楼盘、楼栋和户信息之间的关系可以表示为:
定义1:实体:表示为
,其中,
表示实体E的i个属性,
为属性
的定义域。
定义2:记录:表示为
形式的属性和属性值对的集合。
定义3:关联实体:在实体联系(E-R)中的具有一对多联系的实体称为关联实体,实体集
中表现出一对多的实体联系,即为
。
定义4:关联属性:在一对多联系的两个实体的一方的关键字属性或多方实体的外键属性称为关联属性。
定义5:关联子树:给定一个一对多的实体关系
,则关联子树
定义为如图2所示的二层树,表示两类实体的实例之间对应关系,其中根节点为r,子节点集为
,
。
定义6:关联树T由无数个关联数据集D中一对多关系的关联实体构成的关联子树
组成,
。
关联树T为一个有向无环连通图,节点
和边
。实体
为关联数据集D内实体集
的实体,即
,
,则创建节点
,若实体
与实体
为关联实体,其中
为一方,
为多方,则为节点
创建边
,其中,节点v为父节点,节点w为子节点,即
;如果
则x一定是节点v的子节点,v一定是x的父节点。关联树的根节点
为伪节点,无意义(无输入边的节点是根节点)。每个节点v都有一个标签
,它存储着节点的数据;标签不一定是唯一的。
2.3. 关联树的概念与性质
在一对多关联实体数据集D中,我们将数据集D构建为关联树
。因此对数据集D中关联实体的实体解析问题转为对关联树中
中节点的实体解析问题。比如房地产关联数据集D的盘实体集,栋实体集,户实体集可以依据一对多关联关系构建为关联树
,如图3(a)所示。
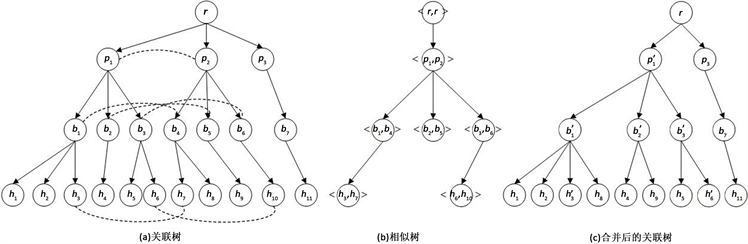
Figure 3. Relevance tree entity resolution
图3. 关联树实体解析
定义7:节点相似度:关联树的任意一个节点都表示为现实世界中的一个具体实体,关联树中任意两个节点v和w的相似度表示为:
,其中
是两个节点的相似度计算函数。
定义8:相似节点:如果两个节点
的相似度
大于规定的阈值
,即
,则认为这两个节点是相似的,记为相似节点对
。相似节点对分为两种情况:
同构相似,指的是两个节点的属性结构相同,属性值的相似度大于给定的阈值;
异构相似,指的是两个节点的属性结构有相交部分,且它们的属性值相似度大于给定的阈值;
引理1:关联树种每层节点都代表一类实体,实体解析中只有实体类别相同才需判断记录是否指向同一实体。因此执行相似度匹配函数的节点
必须为同层节点才有意义,即
。
引理2:关联树中实体间关系为一对多关联关系。在一对多关系中,当且仅当一方为相似节点时,对多方进行相似节点匹配才有意义。比如图1(b)中的房地产数据集D中,只有盘记录集中的
和
相似后,表明两个记录为同一个现实世界中的楼盘实体,因此
关联的子节点集
和
关联的子节点集
才可能包含相似的关联栋节点,有比较的解释意义。即,当两个关联子树的父节点
,若
则比较其子节点集
与
中的节点才有意义(包含相似节点)。
根据引理2,我们可以引申出:
引理3:若关联树
中节点
指向同一现实实体,为相似节点,则其父节点
必然也为相似节点,即
,直至根节点。
由引理3可知,所有相似节点的父节点相似,则关联树中相似节点对具有树形结构,我们将这种具有树形结构的相似节点对集合称为相似树。
定义9:相似子树:如果关联子树对
的根节点对
为相似节点,则我们称关联子树对
为相似子树,其子节点集
可能包含相似节点
,其中
。比如图3(a)中关联子树
与
的根节点
和
相似,依据引理2,关联子树
与
的子节点集可能包含相似节点,即
与
为相似子树。
定义10:相似树:关联树
中相似节点对
具有树型结构,即关联子树对
中相似子节点构成相似树
,相似树中节点表示为相似节点对,边为相似节点对之间的关联关系。相似树
为关联子树对
的子树,分为三种情况:
1) 同构相似,指的是两个根节点及两个根节点下的所有子树的根节点都是同构相似;
2) 异构相似,指的是两个根节点是异构相似,两个根节点下可能存在部分子树的根节点是异构相似;
3) 混合相似,指的是两个根节点存在同构或异构相似,两个根节点下可能部分子树的根节点存在同构或异构相似。
比如图3(a)的关联树
,我们对其中的关联子树进行解析后,组成的似树
如图3(b)所示。
结合引理1、定义6~10可知在一对多关联实体数据集D中,对关联树中
中节点的实体解析问题可以转换为对关联树
进行搜索相似树
的问题。
3. 基于树的一对多关联实体解析方法
本节介绍基于树的一对多关联实体识别方法(Tree-Based Relational Entity Resolution, TB-RER),它借助关联实体间的关联关系实现了关联树模型。TB-RER由两部分组成:关联树搜索算法和节点匹配算法。3.1节介绍关联树搜索算法,3.2节介绍节点匹配算法。
3.1. 关联树搜索算法
一对多关联实体解析不同于传统实体解析,对多类型关联数据进行实体解析。冗余匹配的情况也更为复杂。在一对多关联子树中,我们将匹配可能出现的结果分为以下四种类型:
1) 子节点对相似,根节点对不相似(False Positive)。
2) 子节点对不相似,根节点对不相似(True Negative)。
3) 子节点对相似,根节点对相似(True Positive)。
4) 子节点对不相似,根节点对相似(True Negative)。
其中类型1)、2)和4)为一对多关联实体解析的冗余匹配。
我们提出一个基于深度优先原则的关联树搜索算法
,该算法依据节点的相似性传递(引理2)解决冗余匹配类型1)和2)。
包括三个主要功能模块:节点匹配模块、候选对搜索模块和相似树索引生成模块。涉及两个数据结构:一个相似树索引
和一个候选集Q。
我们对候选集Q中关联子树对
的根节点对
进行相似节点匹配
(第4行),节点匹配模块
将在3.2节中详细说明,如果
,即
,则认为关联子树对
为相似子树,其子节点集
满足引理2,包含的节点对的匹配类型为(3)或(4),即关联子树对
为相似子树。将其子节点集
中的节点对
加入到候选集Q中,其中
满足引理1,
。如果
,即根节点对
不相似,其其子节点集
不满足引理2,包含节点对的匹配类型只包含(1)或(2),不具有匹配意义,阈值
可以通过领域专家给出或者通过实验得到。
我们举例来简单说明这个过程:
以图3(a)的关联树T中的关联子树
为例,其中关联子树对
的根节点
不匹配,则其子节点集
,
不满足引理2,我们对关联子树对
进行剪枝,跳过匹配关联子树对
的子节点集
。虽然
和
的户名都为103但
和
所关联的栋实体不同,
为3号楼103,
为2号楼103,不具备匹配意义,为冗余匹配。关联子树对
的栋节点
匹配,则其子节点集
,
满足引理2,继续对其子节点集的关联子树进行搜索。
若相似节点对
中节点
为非叶子节点,那么相似节点对
的子节点集
中,需要匹配的子节点对有
个,即我们需要执行
次节点匹配函数,这是不现实的。函数LookUp (第6行)输入相似节点对
的子集
,输出节点对
子集
的相似关联子树候选对。我们使用G. Papadakis的分块技术 [5] 对节点对
的子集
中的对象分块,最后生成候选对,加入到候选集Q中。
我们的候选集Q是一个优先队列,用来维持待匹配节点对的解析顺序,Q的每个节点存储一对匹配节点对和相应的优先级。将初始的根节点对输入到LookUp中,将返回的子节点候选匹配对依次插入到候选集Q中,并给予相同的、较低的优先级,节点每深入一层,对LookUp返回的候选匹配节点的优先级提高一级,以便关联树匹配算法能及时的解析出关联树的部分子树,提高解析效率。比如图3(a)的关联树T中的为例,我们先解析候选集Q中的节点对
,优先级为0,
,必相似,我们将节点对
输入到函数LookUp中,将返回的子节点候选对
,加入到候选集Q中,优先级为I,依次匹配
和
,当
相似后,我们基于深度优先原则,将其子集
输入到LookUp中,过滤生成候选节点对
等,加入到候选集Q中,优先级为II,先匹配节点对
,该节点对相似,我们继续深入匹配其子节点集
,
输入到LookUp中过滤生成候选节点对
,
为叶子节点,无子节点,不再深入,匹配其相邻节点,按优先级依次匹配直至候选队列为空。
为了对实体解析顺序的优化,我们在候选集对匹配(第4行)和候选对搜索(第6行)之间对实体解析顺序进行了优化。当节点对
成功匹配后,会搜索候选集中包含
的其他候选对并执行匹配操作。当搜索完所有与
相关的候选对后,我们再添加相似节点对至相似树索引中并对其子节点集进行候选对搜索。比如,当
匹配成功后,在搜索其子节点前先匹配
,若
也成功匹配,则将
整体作为相似节点索引插入到相似索引树中,作为根节点
的子节点,再去搜索
的子节点集的候选对。
相似索引树生成:若候选集Q中节点对
相似节点匹配(第4行)匹配成功后,我们对匹配成功的节点对进行相似树索引构建(第5行),若关联树匹配基于深度优先原则遍历节点对进行匹配,则相似树也基于深度优先顺序进行构建。若关联树匹配基于广度优先原则遍历节点对进行匹配,则相似树也基于广度优先顺序进行构建。
3.2. 节点匹配算法
3.2.1. 传统的基于属性相似度计算
属性相似度计算
设
和
是两个实体,具有n个对齐属性集合
和
,
,我们假定两个实体之间的属性已对齐并作为输入提供。当然,我们的方法也适用于同一实体。让
为
中的记录,并且
和
是属性
和
的值。
相似函数
计算相似度分数,分数的取值范围为[0,1],比如编辑距离和Jaccard相似度。分数越接近1越意味着
和
具有更高的相似性。
属性匹配规则是一个三元组
表示为
的布尔值,其中
是一个属性索引,f是一个相似度函数,
是相似度阈值。属性匹配规则
返回为true意味着
与
相对于特定相似函数f和阈值
匹配。
我们将
作为相似函数f和阈值
的属性匹配规则。在下文中,我们将其简写成
。
记录相似度计算:
记录相似度计算是一组对不同属性的属性相似度计算的结合。我们通常根据属性的重要程度不同为不同的属性
分配不同的权重
,以综合的角度判断记录是否匹配,为了减少其求解的搜索空间,记录相似度计算时,通常将每个属性都采用相同的相似度算法和阈值来进行比较。
当节点为同构节点时,节点与节点同为一类实体,属性一致。当节点为异构节点时,节点与节点为不同实体,属性不一致。将属性对齐后为:
(1)
其中
与
为对齐后的属性。
3.2.2. 基于关联属性的相似度算法
在我们进行传统的属性相似度方法进行相似度计算时,仅计算当前节点属性的相似度判断该节点是否相似,但在关联数据集中,多个实体集之间的具有关联关系,其关联关系由外键属性构成,如图1(a)所示,栋实体集具有盘实体集的共同属性,盘名;户实体集具有栋实体集的共同属性,栋名;在关联实体集中,不仅有当前实体集的属性可以判断是否为同一实体,其关联实体的部分属性也可以判断其是否为同一实体。因此我们将本节点的属性相似度和关联子节点的部分属性相似度结合起来判断当前节点是否匹配。
定义一个关联属性相似度算法
,其中
:
(2)
(3)
其中,
是节点
自身的基于属性的相似度,采用已有的基于属性的相似度算法 [18],
是节点
的关联节点部分属性的相似度,
是自身属性相似度和关联节点属性相似度的权值分配系数,可由用户根据关联节点属性相似度的重要性进行设定。
采用关联属性进行相似度匹配。K为关联节点属性选取个数,由领域专家给出或者通过实验得到。
算法2描述了基于关联属性的相似度算法,该算法输入节点
和权值
,通过计算关联节点的部分属性和自身属性的相似度来计算节点
的综合节点相似度sim,并将综合相似度sim作为输出返回,权值
用于判断关联节点属性相似度与自身节点属性相似度的比重。我们循环搜索节点
的关联节点(第2行)并计算关联节点的部分属性的关联相似度
(第3行),遍历
的属性(第4行),计算节点
的节点相似度
(第5行),最终返回综合相似度sim。
4. 实验与分析
4.1. 实验设置
本文实验采用真实数据来对算法性能进行评测。其中真实数据采用房地产数据集,其数据来源于“面向房地产领域的Web数据抽取”项目所抽取的多个数据源的5个不同时段的房地产关联数据信息,共含有约80万个记录,每个时段的房地产数据集中都包含盘记录表、栋记录表、户信息表。其中盘记录表中约含有3千个记录,包含地址、项目名称、容积率等60余种属性。栋记录表中约含有2万个记录,包含栋名称、楼型等30余种属性。户信息表中约含有15万个记录,包含门牌号、楼层、建筑面积等四十余种属性。我们分别将这五个房地产数据集{d1, d2, d3, d4, d5}分为五个不同大小数据集D1,D2,D3,D4,D5,D1 = {d1},D2 = {d1, d2}……D5 = {d1, d2, ..., d5}。我们将使用数据集D1用于对比实验,再从D1逐渐增加到D5用作可扩展评估。
本文实验代码采用Java编写,运行在配置3.7 GHz AMD Ryzen7 2700X处理器,16 GB内存的64位Windows10操作系统中。
我们使用F1-Score来比较其性能,F1-Score是准确率和召回率的调和均值,其中准确率是所有匹配实体中正确匹配的实体所占比例;召回率是所有应该匹配的实体中正确匹配的实例所占比例;我们使用算法运行时间来测试该算法的可扩展性。
4.2. 方法比较
本文采用基于关联属性的相似度算法来进行节点匹配,该算法基于属性相似度,为了减小其求解的搜索空间,我们对每个属性都采用相同的相似度算法和阈值来进行比较。对于不同的相似度算法,我们经实验选择Jaccard相似度算法来进行实验,经实验测得,我们将3个关联栋实体的属性加入盘实体的匹配中;将2个关联户实体的属性加入栋实体的匹配中,根据实验测得相似度阈值
为0.80,经实验测得权值分配系数
为0.83。
利用房地产数据集,采用上述有效性评测标准,我们将本文提出的关联树搜索算法、传统属性匹配算法和DepGraph算法进行性能比较。如图4所示,分别表示数据集总记录条数在18万,盘实体集3000条,栋实体集2万条,户实体集16万条时,两算法在房地产数据集中的3类实体集的准确性上,仅在盘实体集上与传统方法持平,比DepGraph算法略低,随着关联树的加深,栋实体集和户实体集的解析准确性也优于传统方法和DepGraph算法。
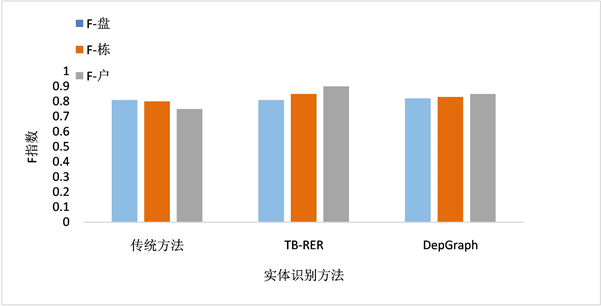
Figure 4. Comparison of TB-RER method and existing methods
图4. TB-RER方法与已有方法对比
4.3. 可扩展评估
为了测试关联树搜索算法的可扩展性,将TB-RER算法分别在规模D1逐渐增加到D5的房地产数据集上进行实验,相邻数据集规模相差大约20 w。观察图5,TB-RER随着数据集规模的增长,其时间开销的增长接近于线性,这得益于关联树模型的相似度传递,使树的匹配层数加深,所需要匹配的节点集远远少于其层的总节点集,并使用分块技术生成候选匹配对,引导实体解析在数据集减少的情况下又以高效的匹配顺序进行,避免了平方级的增长。
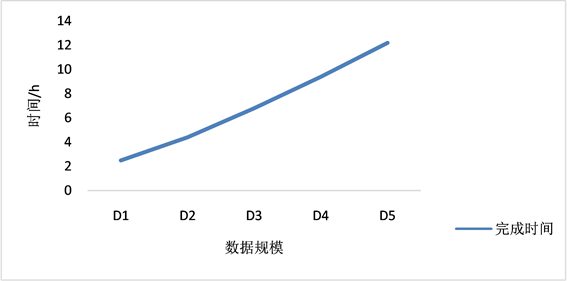
Figure 5. TB-RER scalable evaluation
图5. TB-RER可扩展评估
5. 结论
本文提出了一种基于关联树模型的关联实体解析方法。依据一对多关联实体的相似性传递性质,随着关联树层数加深,实体集的实体数也随之增大,但关联树中搜索的节点的量并没有随之增多,以此提高实体识别的效率。关联树匹配算法可以更快速、准确地查找潜在相似关联实体对;节点匹配算法可以更加精确地匹配相似节点对。实验结果验证了基于关联树模型的关联实体解析方法的有效性,随着树层数加深,效率逐渐远超传统方法,并且可以和现在主流的方法相媲美,甚至更好。
6. 结束语
实体解析是数据挖掘和数据集成的重要组成部分。大数据时代,数据呈现多样性,关联性以及时效性。如何对多类型的、不同时间抓取的、一对多关联关系的对象进行高效、准确的关联实体解析成为一个重要问题。针对已有的关联实体解析方法的不足,本文提出一种基于树模型的关联实体解析方法——TB-RER,该方法适合于一对多关联关系的数据。下一步工作将研究如何对一对多关联实体的解析结果进行实体生成。