具有脉冲的混合时滞Hopfield神经网络的全局渐近稳定性

Global Asymptotic Stability of Hopfield Neural Networks with Mixed Delays and Impulses

摘要: 本文研究一类具有脉冲的混合时滞Hopfield神经网络的全局渐近稳定性，首先利用Brouwer不动点定理和矩阵谱半径证明系统平衡点的存在性和唯一性，再利用Barbalat引理以及构造合适的Lyapunov函数，讨论系统的全局渐近稳定性，最后利用数值仿真验证结论的有效性。

Abstract: This paper studies the global asymptotic stability of a class of Hopfield neural networks with impulsive mixed delays. Firstly, the Brouwer fixed point theorem and the matrix spectral radius are used to prove the existence and uniqueness of the equilibrium point of the system, and then use Barbalat’s lemma and construct a suitable Lyapunov function to discuss the global asymptotic stability of the system. Finally use numerical simulation to verify the validity of the conclusions.

1. 引言

近些年来，由于Hopfield神经网络具有广泛的研究前景，它吸引许多学者的关注。如在文献 [1] 中关于联想记忆方面的应用，在文献 [2] 中针对由物理化学引起线性逆不适定问题的应用，在文献 [3] 中针对环境波动对疾病传播影响的应用，在文献 [4] 中针对改进医疗专家诊断系统的应用。这些应用本质上依赖于系统的动态行为，因此关于Hopfield神经网络的动态行为的研究就具有重要的理论意义和实际意义。

在现有的工作中，多数的模型都涉及到时间延迟和脉冲现象，这里时间延迟有比例时滞 [5]、时变时滞 [6]、分布时滞 [7]、常时滞 [8] 和泄露时滞 [9] 等，这些现象在神经网络中是普遍的且不可避免，它们是发散、振荡、混乱、不稳定和性能不佳的根源，因此，对具有时滞神经网络的研究不仅具有理论意义，而且更具有现实意义。文献 [5] 研究了具有比例时滞Hopfield神经网络的全局渐近稳定性，文献 [6] 利用迭代和不等式技巧，得到具有脉冲的时变时滞的Hopfield神经网络周期解的存在性与一致稳定性的判据，文献 [10] 通过线性矩阵不等式的方法研究了具有时变时滞的Hopfield神经网络的全局渐近稳定性，文献 [7] 通过迭代分析，考虑了具有分布延迟的脉冲Hopfield神经网络的周期解的存在性和平衡点的一致稳定性。

论文基于具有单个时滞或具有脉冲与时滞模型的相关文献启发，将脉冲、时变时滞和分布时滞引入到Hopfield神经网络模型中，利用不动点定理及构造合适的Lyapunov泛函，研究具有脉冲混合时滞的Hopfield神经网络的全局渐近稳定性。

2. 模型与预备知识

考虑如下具有脉冲的混合时滞Hopfield神经网络模型：

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_i\left(t\right)=-c_i{x}_i\left(t\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{a}_{ij}{f}_j\left(x_j\left(t\right)\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{b}_{ij}{f}_j\left(x_j\left(t-{\tau }_{ij}\left(t\right)\right)\right)\\ +\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{d}_{ij}{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)f_j\left(x_j\left(t-s\right)\right)\text{d}s}+I_i,t\ge 0,t\ne t_k\\ \Delta x_i=x_i\left(t_k^{+}\right)-x_i\left(t_k^{-}\right)=I_{ik}\left(x_i\left(t_k\right)\right),t=t_k\\ x_i\left(s\right)={\phi }_i\left(s\right),s\in \left(-\infty ,0\right]\end{array}$ (1)

其中 $i=1,2,\cdots ,n$，n表示神经元的个数； $x_i\left(t\right)$ 表示第i个神经元在t时刻是状态； $c_i>0$ 是自反馈连接权重； $a_{ij}$ 、 $b_{ij}$ 和 $d_{ij}$ 分别表示第j个神经元到第i个神经元的连接权重； ${\tau }_{ij}\left(t\right)$ 表示时变时滞； $f_j$ 表示激活函数； $I_i$ 表示第i个神经元的外部输入； $\Delta x_i\left(t_k\right)$ 是 $t_k$ 时刻的脉冲， $t_1<t_2<\cdots$ 是严格单调递增的数列，并且满足 ${\lim }_{k\to +\infty }{t}_k=+\infty$，这里初始条件 ${\phi }_i\left(s\right)\in \text{C}\left(-\infty ,0\right]$。

现做如下假设：

(H₁) 激活函数 $f_j(\cdot )$ 和 $g_j(\cdot )$ 在R上有界且满足Lipschitz条件，即存在常数 $L_j>0$， $F_j>0$， $H_j>0$， $G_j>0$，使得

$\left|f_j(\cdot )\right|<L_j;\left|f_j\left(u\right)-f_j\left(v\right)\right|\le F_j\left|u-v\right|$

$\left|g_j(\cdot )\right|<H_j;\left|g_j\left(u\right)-g_j\left(v\right)\right|\le G_j\left|u-v\right|$

(H₂) 对于任意 $i,j=1,2,\cdots ,n$， $t>0$， ${\tau }_{ij}\left(t\right):R^{+}\to 0\cup R^{+}$，这里 ${\tau }_{ij}\left(t\right)$ 是连续可微函数，并且 $\left|{{\tau }^{\prime }}_{ij}\left(t\right)\right|<{\alpha }_{ij}$，这里 $0\le {\alpha }_{ij}<1$。

(H₃) 核 $k_{ij}$ 是定义在 $\left[0,+\infty \right)$ 上的实值非负连续函数，其中 $i=1,2,\cdots ,n$， $j=1,2,\cdots ,n$，它满足

${\displaystyle {\int }_0^{+\infty }{k}_{ij}\left(s\right)\text{d}s}=1,{\displaystyle {\int }_0^{+\infty }s{k}_{ij}\left(s\right)\text{d}s}<+\infty .$

定义1 [5] 若对系统(1)的任何初始值 ${\phi }_i\left(s\right)$，都满足

$\underset{t\to \infty }{\lim }\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\left|x_i\left(t\right)-x_i^{*}\right|=0,$

则称系统(1)的平衡点 $x_i^{*}$ 是全局渐近稳定的。

引理1 [11] (Brouwer不动点定理)设D是 $R^n$ 中有界凸闭集， $\Phi :D\to D$ 连续，则 $\Phi$ 在D上必有不动点。

引理2 [11] 设M是非负n阶矩阵，X是非负n维向量，若 $X\ne 0$，存在实数 $\alpha$，使得 $MX\ge \alpha X$，则谱半径 $\rho \left(M\right)\ge \alpha$。

引理3 [12] (Barbalat引理)设 $z\left(t\right)$ 是定义在 $\left[0,+\infty \right)$ 上的非负可积的一致连续函数，则 ${\lim }_{t\to \infty }z\left(t\right)=0$。

注1 $\rho \left(M\right)$ 的谱半径是指矩阵M的最大特征值。

3. 主要结果

3.1. 平衡点的存在性和唯一性

定理1若条件(H₁)和(H₃)成立，且 $\rho \left(M\right)<1$， $c={\min }_{1\le i\le n}{c}_i$， ${\sigma }_i=\inf {{\phi }^{\prime }}_i\left(x_i\right)$ 其中 $M={\left(m_{ij}\right)}_{n\times n}$， $m_{ij}=\frac{\left(\left|a_{ij}\right|+\left|b_{ij}\right|+\left|d_{ij}\right|\right)F_j}{c{\sigma }_i}$，则系统(1)的平衡点存在且唯一。

证明：设 $x^{*}={\left(x_1^{*},x_2^{*},\cdots ,x_n^{*}\right)}^{\text{T}}$ 为系统(1)的平衡点，则有

$-c_i{x}_i^{*}+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{a}_{ij}{f}_j\left(x_j^{*}\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{b}_{ij}{f}_j\left(x_j^{*}\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{d}_{ij}{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)f_j\left(x_j^{*}\right)\text{d}s}+I_i=0,$

由假设条件(H₃)可知 ${\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)\text{d}s}=1$，故上式可写为

$c_i{x}_i^{*}=\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{a}_{ij}{f}_j\left(x_j^{*}\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{b}_{ij}{f}_j\left(x_j^{*}\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{d}_{ij}{f}_j\left(x_j^{*}\right)+I_i$

$x_i^{*}=\frac{1}{c_i}\left[\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{a}_{ij}{f}_j\left(x_j^{*}\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{b}_{ij}{f}_j\left(x_j^{*}\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{d}_{ij}{f}_j\left(x_j^{*}\right)+I_i\right]$

先证系统(1)平衡点的存在性，由假设(H₁)有

$\begin{array}{l}\left|\frac{1}{c_i}\left[\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{a}_{ij}{f}_j\left(x_j^{*}\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{b}_{ij}{f}_j\left(x_j^{*}\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{d}_{ij}{f}_j\left(x_j^{*}\right)+I_i\right]\right|\\ \le \frac{1}{c_i}\left[\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|a_{ij}\right|L_j+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ij}\right|L_j+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ij}\right|L_j+I_i\right]=P_i\end{array}$

令 ${\phi }_i\left(x^{*}\right)=x_i^{*}=\frac{1}{c_i}\left[{\displaystyle {\sum }_{j=1}^n{a}_{ij}{f}_j\left(x_j^{*}\right)}+{\displaystyle {\sum }_{j=1}^n{b}_{ij}{f}_j\left(x_j^{*}\right)}+{\displaystyle {\sum }_{j=1}^n{d}_{ij}{f}_j\left(x_j^{*}\right)}+I_i\right]$，则有 ${\phi }_i\in \left[-P_i,P_i\right]=D_i$，

$i=1,2,\cdots ,n$，令 $\phi ={\left({\phi }_1,{\phi }_2,\cdots ,{\phi }_n\right)}^{\text{T}}={\left(x_1^{*},x_2^{*},\cdots ,x_n^{*}\right)}^{\text{T}}$，易知 $\phi :D\to D$ 连续有界，由引理1可知， $\phi$ 在D上必有不动点，因此系统(1)的平衡点存在。

下证平衡点的唯一性。设 $x^{*}=\left(x_1^{*},x_2^{*},\cdots ,x_n^{*}\right)$ 和 $y^{*}=\left(y_1^{*},y_2^{*},\cdots ,y_n^{*}\right)$ 是系统(1)的平衡点， $\eta =x^{*}-y^{*}\ne 0$， ${\eta }_i=x_i^{*}-y_i^{*}$， $i=1,2,\cdots ,n$。

$c_i{\phi }_i\left(x_i^{*}\right)-c_i{\phi }_i\left(y_i^{*}\right)=c_i{{\phi }^{\prime }}_i\left({\xi }_i\right)\left(x_i^{*}-y_i^{*}\right)=\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left(a_{ij}+b_{ij}+d_{ij}\right)\left(f_j\left(x_j^{*}\right)-f_j\left(y_j^{*}\right)\right),$

其中 ${\xi }_i$ 是介于 $x_i^{*}$ 和 $y_i^{*}$ 之间，故有

$\begin{array}{c}\left|{\eta }_i\right|=\left|\frac{1}{c_i{{\phi }^{\prime }}_i\left({\xi }_i\right)}\left(\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left(a_{ij}+b_{ij}+d_{ij}\right)\left(f_j\left(x_j^{*}\right)-f_j\left(y_j^{*}\right)\right)\right)\right|\\ \le \frac{1}{c_i{{\phi }^{\prime }}_i\left({\xi }_i\right)}\left(\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left(\left|a_{ij}\right|+\left|b_{ij}\right|+\left|d_{ij}\right|\right)F_j\left|x_j^{*}-y_j^{*}\right|\right)\\ =\frac{1}{c_i{{\phi }^{\prime }}_i\left({\xi }_i\right)}\left(\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left(\left|a_{ij}\right|+\left|b_{ij}\right|+\left|d_{ij}\right|\right)F_j\left|{\eta }_j\right|\right)\\ \le \frac{1}{c{\sigma }_i}\left(\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left(\left|a_{ij}\right|+\left|b_{ij}\right|+\left|d_{ij}\right|\right)F_j\left|{\eta }_j\right|\right)\\ =\frac{{{\displaystyle \sum }}_{j=1}^n\left(\left|a_{ij}\right|+\left|b_{ij}\right|+\left|d_{ij}\right|\right)F_j}{c{\sigma }_i}\left|{\eta }_j\right|\end{array}$

其中 $c={\min }_{1\le i\le n}{c}_i$， ${\sigma }_i=\inf {{\phi }^{\prime }}_i\left(x_i\right)$， $m_{ij}=\frac{\left(\left|a_{ij}\right|+\left|b_{ij}\right|+\left|d_{ij}\right|\right)F_j}{c{\sigma }_i}$，即 $\left|\eta \right|\le M\left|\eta \right|$，这里 $\left|\eta \right|$ 表示n列向量， $\left|\eta \right|={\left(\left|{\eta }_1\right|,\left|{\eta }_2\right|,\cdots ,\left|{\eta }_n\right|\right)}^{\text{T}}$，由引理2知，若 $\eta \ne 0$，则 $\rho \left(M\right)\ge 1$，这与定理 $\rho \left(M\right)<1$ 矛盾，因此 $\eta =0$，即 $x^{*}=y^{*}$，故该系统存在唯一平衡点。

3.2. 平衡点的全局渐近稳定性

定理2设 $z_i\left(t_k\right)={\lambda }_{ik}{z}_i\left(t_k^{-}\right)$， $\left|{\lambda }_{ik}\right|\le 1$，若条件(H₁)~(H₃)成立，且

$\lambda =\underset{1\le i\le n}{\min }\left\{c_i-H_i\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left(\left|a_{ji}\right|+\frac{\left|b_{ji}\right|}{1-{\alpha }_{ji}}+\left|d_{ji}\right|\right)\right\}\ge 0$

则系统(1)的平衡点是全局渐近稳定的。

证明：设 $x^{*}=\left(x_1^{*},x_2^{*},\cdots ,x_n^{*}\right)$ 是系统(1)的平衡点， $x\left(t\right)=\left(x_1\left(t\right),x_2\left(t\right),\cdots ,x_n\left(t\right)\right)$ 是系统任意解，令 $z\left(t\right)=x\left(t\right)-x^{*}$，

$\begin{array}{c}\stackrel{\dot{}}{z}\left(t\right)=-c_i{x}_i\left(t\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{a}_{ij}{f}_j\left(x_j\left(t\right)\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{b}_{ij}{f}_j\left(x_j\left(t-{\tau }_{ij}\left(t\right)\right)\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{d}_{ij}{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)f_j\left(x_j\left(t-s\right)\right)\text{d}s}\\ -c_i{x}_i^{*}-\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{a}_{ij}{f}_j\left(x_j^{*}\right)-\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{b}_{ij}{f}_j\left(x_j^{*}\right)-\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{d}_{ij}{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)f_j\left(x_j^{*}\right)\text{d}s}\\ =-c_i{z}_i\left(t\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{a}_{ij}\left[f_j\left(x_j\left(t\right)\right)-f_j\left(x_j^{*}\right)\right]+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{b}_{ij}\left[f_j\left(x_j\left(t-{\tau }_{ij}\left(t\right)\right)\right)-f_j\left(x_j^{*}\right)\right]\\ +\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{d}_{ij}\left[{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)f_j\left(x_j\left(t-s\right)\right)\text{d}s}-{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)f_j\left(x_j^{*}\right)\text{d}s}\right]\\ =-c_i{z}_i\left(t\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{a}_{ij}{g}_j\left(z_j\left(t\right)\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{b}_{ij}{g}_j\left(z_j\left(t-{\tau }_{ij}\left(t\right)\right)\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{d}_{ij}{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)g_j\left(z_j\left(t-s\right)\right)\text{d}s}\end{array}$

因此有

$\{\begin{array}{l}\stackrel{\dot{}}{z}\left(t\right)=-c_i{z}_i\left(t\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{a}_{ij}{g}_j\left(z_j\left(t\right)\right)+\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{b}_{ij}{g}_j\left(z_j\left(t-{\tau }_{ij}\left(t\right)\right)\right)\\ +\underset{j=1}{\overset{n}{{\displaystyle \sum }}}{d}_{ij}{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)g_j\left(z_j\left(t-s\right)\right)\text{d}s},t\ge 0,t\ne t_k\\ \Delta z_i\left(t_k\right)=z_i\left(t_k^{+}\right)-z_i\left(t_k^{-}\right)=H_{ik}\left(y_i\left(t_k\right)\right),t=t_k\\ z_i\left(s\right)={\phi }_i\left(s\right)-x_i^{*},s\in \left(-\infty ,0\right]\end{array}$ (2)

其中 $g_j\left(z_j\left(t\right)\right)=f_j\left(x_j^{*}+z_j\left(t\right)\right)-f_j\left(x_j^{*}\right)$， $g_j\left(z_j\left(t-{\tau }_{ij}\left(t\right)\right)\right)=f_j\left(x_j^{*}+z_j\left(t-{\tau }_{ij}\left(t\right)\right)\right)-f_j\left(x_j^{*}\right)$，要研究系统(1)平衡点的稳定性，只需研究系统(2)零解的稳定性即可。

故构造如下正定的Lyapunov函数

$v\left(t\right)=\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\left|z_i\left(t\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ij}\right|H_j{\displaystyle {\int }_{t-{\tau }_{ij}\left(t\right)}^t\frac{\left|z_j\left(s\right)\right|}{1-{\alpha }_{ij}}\text{d}s}+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ij}\right|H_j{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)}{\displaystyle {\int }_{t-s}^t\left|z_j\left(r\right)\right|\text{d}r\text{d}s},$ (3)

沿系统(2)对上述Lyapunov函数求导，可得

$\begin{array}{c}\stackrel{\dot{}}{v}\left(t\right)=\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\left|{\stackrel{\dot{}}{z}}_i\left(t\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ij}\right|H_j\left[\frac{\left|z_j\left(t\right)\right|}{1-{\alpha }_{ij}}-\frac{\left|z_j\left(t-{\tau }_{ij}\left(t\right)\right)\left(1-{\stackrel{\dot{}}{\tau }}_{ij}\left(t\right)\right)\right|}{1-{\alpha }_{ij}}\right]\\ +\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ij}\right|H_j{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)\left(\left|z_j\left(t\right)\right|-\left|z_j\left(t-s\right)\right|\right)\text{d}s}\\ \le -\underset{i=1}{\overset{n}{{\displaystyle \sum }}}{c}_i\left|z_i\left(t\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|a_{ij}\right|\left|g_j\left(z_j\left(t\right)\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ij}\right|\left|g_j\left(z_j\left(t-{\tau }_{ij}\left(t\right)\right)\right)\right|\\ +\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ij}\right|{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)g_j\left(z_j\left(t-s\right)\right)\text{d}s}+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ij}\right|H_j\frac{\left|z_j\left(t\right)\right|}{1-{\alpha }_{ij}}\\ -\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ij}\right|H_j\frac{\left|z_j\left(t-{\tau }_{ij}\left(t\right)\right)\left(1-{\stackrel{\dot{}}{\tau }}_{ij}\left(t\right)\right)\right|}{1-{\alpha }_{ij}}+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ij}\right|H_j{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)\left|z_j\left(t\right)\right|\text{d}s}\end{array}$

$\begin{array}{l}-\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ij}\right|H_j{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)\left|z_j\left(t-s\right)\right|\text{d}s}\\ \le -\underset{i=1}{\overset{n}{{\displaystyle \sum }}}{c}_i\left|z_i\left(t\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|a_{ij}\right|H_j\left|z_j\left(t\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ij}\right|H_j\left|z_j\left(t-{\tau }_{ij}\left(t\right)\right)\right|\\ +\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ij}\right|{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)H_j\left|z_j\left(t-s\right)\right|\text{d}s}+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ij}\right|H_j\frac{\left|z_j\left(t\right)\right|}{1-{\alpha }_{ij}}\\ -\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ij}\right|H_j\left|z_j\left(t-{\tau }_{ij}\left(t\right)\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ij}\right|H_j{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)\left|z_j\left(t\right)\right|\text{d}s}\\ -\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ij}\right|H_j{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)\left|z_j\left(t-s\right)\right|\text{d}s}\end{array}$

$\begin{array}{l}=-\underset{i=1}{\overset{n}{{\displaystyle \sum }}}{c}_i\left|z_i\left(t\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|a_{ij}\right|H_j\left|z_j\left(t\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ij}\right|H_j\frac{\left|z_j\left(t\right)\right|}{1-{\alpha }_{ij}}+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ij}\right|H_j\left|z_j\left(t\right)\right|\\ =-\underset{i=1}{\overset{n}{{\displaystyle \sum }}}{c}_i\left|z_i\left(t\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|a_{ji}\right|H_i\left|z_i\left(t\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ji}\right|H_i\frac{\left|z_i\left(t\right)\right|}{1-{\alpha }_{ji}}+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ji}\right|H_i\left|z_i\left(t\right)\right|\\ =-\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\left(c_i-H_i\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left(\left|a_{ji}\right|+\frac{\left|b_{ji}\right|}{1-{\alpha }_{ji}}+\left|d_{ji}\right|\right)\right)\left|z_i\left(t\right)\right|\\ \le -\lambda \underset{i=1}{\overset{n}{{\displaystyle \sum }}}\left|z_i\left(t\right)\right|,\end{array}$ (4)

其中 $\lambda ={\min }_{1\le i\le n}\left\{c_i-H_i{\displaystyle {\sum }_{j=1}^n\left(\left|a_{ji}\right|+\frac{\left|b_{ji}\right|}{1-{\alpha }_{ji}}+\left|d_{ji}\right|\right)}\right\}\ge 0$，由定理2和(3)式可知 $\stackrel{\dot{}}{v}\left(t\right)\le 0$，这里 $t>0$ 且 $t\ne t_k$。

当 $t=t_k$ 时，由(3)式和 $\left|{\lambda }_{ik}\right|\le 1$ 有

$\begin{array}{c}v\left(t_k\right)=\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\left|z_i\left(t_k\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ij}\right|H_j{\displaystyle {\int }_{t_k-{\tau }_{ij}\left(t_k\right)}^{t_k}\frac{\left|z_j\left(s\right)\right|}{1-{\alpha }_{ij}}\text{d}s}+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ij}\right|H_j{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)}{\displaystyle {\int }_{t_k-s}^{t_k}\left|z_j\left(r\right)\right|\text{d}r\text{d}s}\\ =\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\left|{\lambda }_{ik}{z}_i\left(t_k^{-}\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ij}\right|H_j{\displaystyle {\int }_{t_k^{-}-{\tau }_{ij}\left(t_k^{-}\right)}^{t_k^{-}}\frac{\left|z_j\left(s\right)\right|}{1-{\alpha }_{ij}}\text{d}s}+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ij}\right|H_j{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)}{\displaystyle {\int }_{t_k^{-}-s}^{t_k^{-}}\left|z_j\left(r\right)\right|\text{d}r\text{d}s}\\ \le \underset{i=1}{\overset{n}{{\displaystyle \sum }}}\left|z_i\left(t_k^{-}\right)\right|+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|b_{ij}\right|H_j{\displaystyle {\int }_{t_k^{-}-{\tau }_{ij}\left(t_k^{-}\right)}^{t_k^{-}}\frac{\left|z_j\left(s\right)\right|}{1-{\alpha }_{ij}}\text{d}s}+\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|d_{ij}\right|H_j{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)}{\displaystyle {\int }_{t_k^{-}-s}^{t_k^{-}}\left|z_j\left(r\right)\right|\text{d}r\text{d}s}\\ =v\left(t_k^{-}\right)\end{array}$

综上可得当 $t\in \left[0,+\infty \right)\cup \left\{t_k\right\}$ 时， $\stackrel{\dot{}}{v}\left(t\right)\le 0$，现对(4)式两边积分可得

$z\left(t\right)+\lambda {\displaystyle {\int }_0^t\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\left|z_i\left(s\right)\right|\text{d}s}\le z\left(0\right),$

所以 $\left|z_i\left(t\right)\right|$ 是有界的，即存在常数 $N>0$，使 $\left|z_i\left(t\right)\right|\le N$，再由(4)式可知 $\left|{\stackrel{\dot{}}{z}}_i\left(t\right)\right|$ 在 $\left[0,+\infty \right)\cup \left\{t_k\right\}$ 上有上界，从而 ${\displaystyle {\sum }_{i=1}^n\left|z_i\left(t\right)\right|}$ 在 $\left[0,+\infty \right)\cup \left\{t_k\right\}$ 上一致连续由引理3知 ${\lim }_{t\to +\infty }\left|z_i\left(t\right)\right|=0$，即 ${\lim }_{t\to +\infty }\left|x_i\left(t\right)-x_i^{*}\right|=0$，因此系统(2)的零解是全局渐近稳定的，从而系统(1)的平衡点是全局渐近稳定的。

推论1 若条件(H₁)~(H₃)成立，且 $z_i\left(t_k\right)={\lambda }_{ik}{z}_i\left(t_k^{-}\right)$， $\left|{\lambda }_{ik}\right|\le 1$

1) 当 $d_{ij}=0$ 时，不等式 ${\min }_{1\le i\le n}\left\{c_i-H_i{\displaystyle {\sum }_{j=1}^n\left(\left|a_{ji}\right|+\left|d_{ji}\right|\right)}\right\}\ge 0$ 成立；

2) 当 $b_{ij}=0$ 时，不等式 ${\min }_{1\le i\le n}\left\{c_i-H_i{\displaystyle {\sum }_{j=1}^n\left(\left|a_{ji}\right|+\frac{\left|b_{ji}\right|}{1-{\alpha }_{ji}}\right)}\right\}\ge 0$ 成立，

则系统(1)的平衡点是全局渐近稳定的。

注2 当 $d_{ij}=0$ 时，系统(1)变成具有脉冲的时变时滞Hopfield神经网络模型，此模型与文献 [6] 和 [10] 模型一致，故用本文方法亦可得到文献 [6] 和 [10] 模型中平衡点的全局渐近稳定，与文献 [10] 线性矩阵不等式的方法相比本文所用的方法得到的判据更容易验证。

注3 当 $b_{ij}=0$ 时，系统(1)变成文献 [7] 模型中的特殊形式，故可用此方法得到文献 [7] 中模型的全局渐近稳定。

4. 数据仿真

考虑如下具有脉冲的二维混合时滞Hopfield神经网络，

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_i\left(t\right)=-c_i{x}_i\left(t\right)+\underset{j=1}{\overset{2}{{\displaystyle \sum }}}{a}_{ij}{f}_j\left(x_j\left(t\right)\right)+\underset{j=1}{\overset{2}{{\displaystyle \sum }}}{b}_{ij}{f}_j\left(x_j\left(t-{\tau }_{ij}\left(t\right)\right)\right)\\ +\underset{j=1}{\overset{2}{{\displaystyle \sum }}}{d}_{ij}{\displaystyle {\int }_0^{\infty }{k}_{ij}\left(s\right)f_j\left(x_j\left(t-s\right)\right)\text{d}s}+I_i,t\ge 0,t\ne t_k\\ \Delta x_i=x_i\left(t_k^{+}\right)-x_i\left(t_k^{-}\right)=I_{ik}\left(x_i\left(t_k\right)\right),t=t_k\\ x_i\left(s\right)={\phi }_i\left(s\right),s\in \left(-\infty ,0\right]\end{array}$

其中 $A=\left(\begin{array}{cc}0.2& -0.1\\ 0.1& 0.5\end{array}\right)$， $B=\left(\begin{array}{cc}-0.5& 0.5\\ 0.1& -0.3\end{array}\right)$， $C=\left(\begin{array}{cc}2& 0\\ 0& 3\end{array}\right)$， $D=\left(\begin{array}{cc}0.2& 0.5\\ 0.2& -0.3\end{array}\right)$， $I={\left(0,0\right)}^{\text{T}}$，变时滞 ${\tau }_{11}\left(t\right)=1+\frac{1}{2}\sin t$， ${\tau }_{12}\left(t\right)=1-\frac{1}{2}\sin t$， ${\tau }_{21}\left(t\right)=1+\frac{1}{2}\cos t$， ${\tau }_{22}\left(t\right)=1-\frac{1}{2}\cos t$，取激活函数 $f_j\left(x_j\left(t\right)\right)=\frac{1}{4}\left(\left|x_j\left(t\right)-1\right|+\left|x_j\left(t\right)+1\right|\right)$，函数 ${\phi }_i\left(x_i\left(t\right)\right)=x_i\left(t\right)$，其中 $i,j=1,2$，显然 ${\sigma }_i=\inf {{\phi }^{\prime }}_i\left(x_i\left(t\right)\right)=1$，Lipschitz常数 $H_i=L_i=1$，经计算

$M=\left(\begin{array}{cc}0.45& 0.55\\ 0.2& 0.55\end{array}\right),\rho \left(M\right)\approx 0.8354<1;$

$\lambda =\underset{1\le i\le 2}{\min }\left\{c_i-H_i\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left(\left|a_{ji}\right|+\frac{\left|b_{ji}\right|}{1-{\alpha }_{ji}}+\left|d_{ji}\right|\right)\right\}=\underset{1\le i\le 2}{\min }\left\{0.3417,0.475\right\}=0.3417>0$

这里 ${\left({\alpha }_{ij}\right)}_{2\times 2}=\left(\begin{array}{cc}0.2& 0.7\\ 0.2& 0.4\end{array}\right)$，满足定理1和定理2的条件，由定理1和定理2知系统(1)的平衡点是全

局渐近稳定的，如图1和图2在外部输入为零的情况下不带脉冲和带脉冲的时间响应图。

5. 结论

本文利用不动点定理及构造合适的Lyapunov泛函，研究了具有脉冲的混合时滞Hopfield神经网络平衡点的存在性和唯一性，最后利用数值仿真验证结论的有效性。得到与时滞无关的全局渐近稳定的判据，对不确定的时变时滞仍然可以很好地利用此结论。

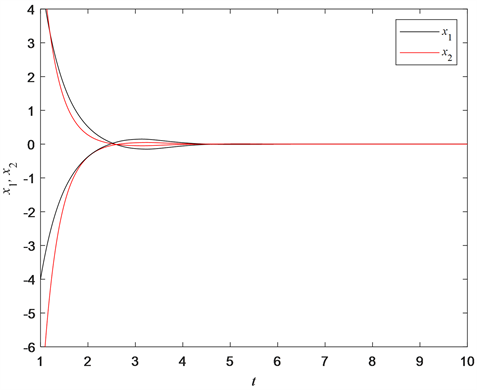
Figure 1. State curve of $x\left(t\right)$ without pulse in system (1)

图1. 系统(1)中 $x\left(t\right)$ 不带脉冲的状态曲线图

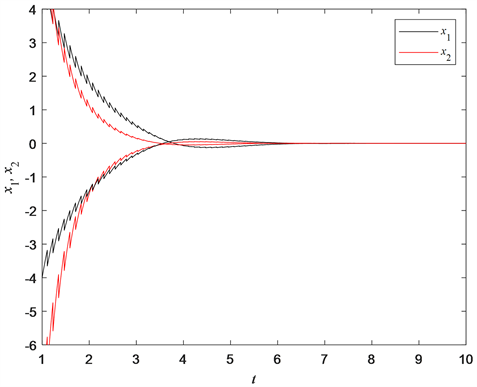
Figure 2. State curve of $x\left(t\right)$ pulse in system (1)

图2. 系统(1)中 $x\left(t\right)$ 带脉冲的状态曲线图

致谢

本论文在陈展衡老师的悉心指导下完成的，老师严谨的教学态度和系统的科研思路给予我写作的想法和思路，同时他平易近人、和蔼可亲的生活作风也给我留下深刻的印象，在此，谨向导师表示崇高的敬意和衷心的感谢。其次感谢伊犁师范大学提供的学习环境，感谢数学与统计学院的领导和授课老师在生活和学习上提供的帮助和指导，感谢同学和朋友在学习和生活上对我的帮助，因为有你们，我才更坚定我的选择。最后感谢汉斯出版社提供的平台。

基金项目

国家自然科学基金项目(61663045)。

NOTES

^*第一作者。

^#通讯作者。