目标检测的损失函数研究进展

Research Progress of Loss Function in Object Detection

摘要: 损失函数是目标检测中的一个研究热点。在深度学习飞速发展的过程中，目标检测算法取得众多研究成果，并广泛应用于人脸检测、门禁识别、自动驾驶等领域。为了进一步了解目标检测的发展细节，本文从目标检测的损失函数优化出发，梳理概括近年来目标检测中分类损失和回归损失的发展进程，并对其进行归类、分析。首先介绍分类损失的发展历程，然后介绍回归损失的两大发展方向：基于L_n范数与基于交并比(IoU)的损失函数，并分析这些损失函数的优缺点以及相互之间的关联性。最后，对基于目标检测的损失函数的未来发展方向进行展望。

Abstract: Loss function is a research hotspot in object detection. With the rapid development of deep learning, object detection algorithms have achieved many research results, and are widely used in face detection, access control recognition, and automatic driving and so forth. In order to further understand the development details of object detection, this article starts from the optimization of the loss function of object detection, combs and summarizes the development process of classification loss and regression loss in object detection in recent years, and classifies and analyzes them. First introduce the development history of classification loss, and then introduce the two major development directions of regression loss: loss function based on L_n norm and based on Intersection over Union (IoU), and analyze the advantages and disadvantages of these loss functions and the correlation between them. Finally, the future development direction of the loss function based on object detection is prospected.

1. 引言

目标检测是计算机视觉的三大任务之一，同时也是其他视觉任务的基石，因此目标检测的发展对计算机视觉具有重要意义。近年来，随着深度学习的快速发展，目标检测在数据预处理、网络结构、损失函数以及后处理等方面取得了丰硕的成果。

损失函数用于指导网络的训练，决定网络的优化方向，因此在目标检测算法中具有重要的地位。目标检测的损失函数分为分类损失和回归损失，其中分类损失用于指导网络对目标预测正确的类别，回归损失用于指导网络生成定位准确的回归框。在检测网络如R-CNN系列 [1] - [7]、Yolo系列 [8] [9] [10] [11]、SSD系列 [12] [13]、以及Transformer系列 [14] 中，常用的分类损失有Cross Entroy Loss [15]、Focal Loss [16] 等，常用的回归损失有L₁ Loss [7]、L₂ Loss [1]、Smooth L₁ Loss [2]、Balanced L₁ Loss [6]、IoU系列损失函数 [17] [18] [19] [20] 等。

本文将分别从分类损失与回归损失介绍目标检测损失函数的研究进展。

2. 分类损失的研究现状

2.1. Cross Entroy Loss

网络预测的分类结果并不是0~1之间的概率值，因此在计算样本分类损失之前，需要通过Softmax或Sigmoid函数得到样本属于各个类别的概率，此处以Softmax为例进行介绍。

令向量V表示一个样本预测的多个类别的预测结果，V_i表示该样本属于第i类的预测结果，为了将预测结果映射到0~1之间保证概率的非负性与归一化，同时保证样本属于所有类别的概率之和为1。通过Softmax对预测结果进行映射，则样本属于第i类的概率为：

$p=S_i=\frac{{\text{e}}^{V_i}}{{\displaystyle {\sum }_i{\text{e}}^{V_j}}}$

交叉熵是用来衡量预测结果与标签概率分布的差异的参数，交叉熵越大，说明预测结果越差，此时交叉熵损失对网络的惩罚也就越大。以二分类任务为例，类别y的取值为 $\left\{+1,-1\right\}$，其中+1代表正类，−1代表负类。假设p是该样本属于正类的概率，则交叉熵损失函数如公式(1)所示：

$L_{CE}=-\log \left(p_t\right)$ (1)

其中：

$p_t=\{\begin{array}{l}p,\text{if}y=1\\ 1-p,\text{otherwise}\end{array}$

2.2. Focal Loss

一阶段算法中，难易样本分类难度差异与正负样本数量不平衡是导致分类效果差的原因：难分类样本与正样本对损失函数贡献少且所占比例低。因此为了提高模型的精度，平衡一阶段算法中难易样本以及正负样本对损失函数的贡献，Focal Loss在交叉熵损失函数的基础上进行改进：通过引入调制系数 ${\left(1-p_t\right)}^{\gamma }$，赋予难分类样本较大的权重，易分类样本较小的权重；通过引入权重系数 $\alpha \in \left[0,1\right]$ 增加正样本的权重，减小负样本的权重，具体计算如公式(2)所示：

$L_{FL}=-{\alpha }_t{\left(1-p_t\right)}^{\gamma }\log \left(p_t\right)$ (2)

其中 ${\alpha }_t$ 的定义与 $p_t$ 类似：

${\alpha }_t=\{\begin{array}{l}\alpha ,\text{if}y=1\\ 1-\alpha ,\text{otherwise}\end{array}$

其中 $\alpha =0.25$， $\gamma =2$。

3. 回归损失研究现状

3.1. L_n Loss

L_n Loss是计算候选框与真实框相应参数的L_n范数。真实框的坐标为 $\left(G_x,G_y,G_w,G_h\right)$，候选框的坐标为 $\left(P_x,P_y,P_w,P_h\right)$，网络要学习一个线性映射 $\phi$，使得对候选框进行映射之后的坐标与真实框的坐标无限接近，即 $\phi \left(P_x,P_y,P_w,P_h\right)=\left(\widehat{G_x},\widehat{G_y},\widehat{G_w},\widehat{G_h}\right)\approx \left(G_x,G_y,G_w,G_h\right)$。对于线性映射的训练，优化项为：

则此时对应的L_n Loss为 $L_n=\sqrt[n]{{\displaystyle \sum {\left(t\right)}^n}}$，其中 $t=t_i-t_i^{\star }$， $i\in \left\{x,y,w,h\right\}$。

3.1.1. L₁ Loss

L₁ Loss又被称为最小绝对误差函数，可以用来度量两个向量之间的差异，损失函数形式如公式(3)所示。

$L_1\left(t\right)={\displaystyle \sum \left|t\right|}$ (3)

$\frac{\text{d}{L}_1\left(t\right)}{\text{d}t}=\{\begin{array}{l}1,t\ge 0\\ -1,t<0\end{array}$ (4)

L₁ Loss图像如图1蓝色曲线所示，其导数形式如公式(4)所示。由于其梯度是常数，因此在训练过程中可以保持稳定的梯度使得模型得以收敛。也正因为梯度为常数，对于收敛之后的模型，较小的误差也采用同样的梯度，因此在极值点附近容易发生震荡，导致模型难以达到更高的精度。

3.1.2. L₂ Loss

L₂ Loss又被称为均方误差函数，也是用来度量两个向量之间的差异，与L₁ Loss略有不同，损失函数形式如公式(5)所示。

$L_2\left(t\right)={\displaystyle \sum {\left(t\right)}^2}$ (5)

$\frac{\text{d}{L}_2\left(t\right)}{\text{d}t}=2t$ (6)

L₂范数函数图像如图1橙色曲线所示，其导数形式如公式(6)所示。函数连续且处处可导，并且随着误差值的减小，梯度也减小，有利于收敛到最小值，但同时训练初期误差值较大，梯度也大，容易产生梯度爆炸导致模型无法收敛，因此使用L₂范数作为损失函数时，往往使用较小的学习率从而避免训练初期梯度爆炸。

Figure 1. L_n Loss function curve

图1. L_n Loss函数曲线

3.1.3. Smooth L₁ Loss

Smooth L₁ Loss函数形式如公式(7)所示：

$\text{Smooth}{L}_1\left(t\right)=\{\begin{array}{l}0.5t^2\left|t\right|<1\\ \left|t\right|-0.5\text{otherwise}\end{array}$ (7)

$\frac{\text{dSmooth}{L}_1\left(t\right)}{\text{d}t}=\{\begin{array}{l}t\left|t\right|<1\\ \pm 1\text{otherwise}\end{array}$ (8)

Smooth L₁ Loss函数图像如图1绿色曲线所示，其导数形式如公式(8)所示。由求导过程可知，Smooth L₁ Loss在损失较大时，按照一个恒定的速率梯度下降，损失较小时，不再按照一个恒定的梯度下降，而是按照变量自身进行动态调整。Smooth L₁ Loss结合了L₁ Loss与L₂ Loss的优点：模型开始训练时，损失较大，采用L₁ Loss的形式，使网络保持稳健的梯度；模型收敛时，当损失较小时采用L₂ Loss的形式，使模型可以收敛到更高的精度。

3.1.4. Balanced L₁ Loss

受Smooth L₁ Loss的启发，为了平衡难易样本对梯度的影响，Balanced L₁ Loss在Smooth L₁ Loss的梯度公式上进行改进，设计L_b的梯度如公式(9)所示：

$\frac{\text{d}{L}_b\left(t\right)}{\text{d}t}=\{\begin{array}{l}\alpha \ln \left(b\left|t\right|+1\right)\left|t\right|<1\\ \gamma \text{otherwise}\end{array}$ (9)

其中， $\alpha$ 控制简单样本的梯度， $\gamma$ 控制调整回归误差的上界，能够使不同任务间更加平衡。 $\alpha$， $\gamma$ 分别从样本和任务层面控制平衡，使网络得到更加平衡的训练。

对梯度公式(9)进行积分，得到L_b的表达式如公式(10)所示：

$L_b\left(t\right)=\{\begin{array}{l}\frac{\alpha }{b}\left(b\left|t\right|+1\right)\ln \left(b\left|t\right|+1\right)-\alpha \left|t\right|\text{if}\left|t\right|<1\\ \gamma \left|t\right|+C\text{otherwise}\end{array}$ (10)

其中 $\alpha =0.5$， $\gamma =1.5$， $\alpha \ln \left(b+1\right)=\gamma$。

3.2. IoU-Based Loss

由于L_n Loss是将候选框的中心点坐标以及长宽四个参数视为互不相关的变量分别进行优化，但实际上这些变量是相关的，因此会导致回归框定位不准确；此外，L_n Loss对尺度敏感，无法做到尺度归一化，并且L_n Loss并不能很好地反映候选框的回归情况。由此开启了IoU (Intersection over Union)-based Loss的研究，IoU是评价候选框回归情况质量的度量函数，优化度量函数本身要比优化代理损失函数更加直观，并且IoU将候选框作为整体进行优化，同时具有尺度不变性，避开了L_n Loss的缺点。

3.2.1. IoU Loss

在目标检测中，IoU是两个框的交并比，定义如公式(11)所示：

$\text{IoU}\left(P,G\right)=\frac{P\cap G}{P\cup G}$ (11)

其中P、G分别表示预测框与真实框，IoU的直观表示如图2所示：

Figure 2. IoU schematic diagram

图2. IoU示意图

IoU Loss的损失函数如公式(12)所示，易知IoU的取值范围是[0, 1]，IoU的值越接近1，说明候选框与真实框越接近，定位越准确，此时损失函数值越小，惩罚也就越小，反之惩罚越大。但同时也可看出IoU Loss的缺点是当候选框与真实框不相交时，IoU为0，L_IoU为常数1，梯度无法回传。

$L_{\text{IoU}}=1-\text{IoU}\left(P,G\right)$ (12)

3.2.2. GIoU Loss

由上述分析可知，IoU Loss只关注重叠部分，无法回归候选框与真实框不相交的情况。为了克服这

一缺点，GIoU Loss在IoU Loss的基础上引入惩罚项 $R=\frac{\left|C-P\cup G\right|}{\left|C\right|}$，其中C是两框的最小闭包，GIoU Loss

由公式(13)定义：

$L_{\text{GIoU}}=1-\text{IoU}+\frac{\left|C-P\cup G\right|}{\left|C\right|}$ (13)

惩罚项R如图3所示，左图是两框相交的情况，右图是两框不相交的情况，可以直观看出GIoU Loss不仅关注两框重叠部分，还关注非重叠部分，对于非重叠部分大的样本加以更大的权重。

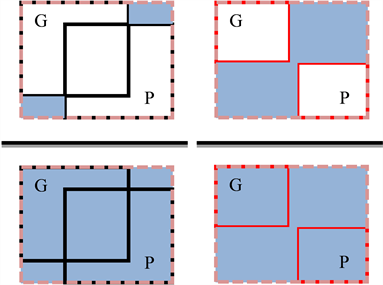
Figure 3. GIoU schematic diagram of penalty items

图3. GIoU惩罚项示意图

3.2.3. DIoU Loss

虽然GIoU Loss解决了两框不相交无法回归的情况，但是当两框处于包含关系时，GIoU Loss退化为IoU Loss，无法反映不同位置下回归情况的好坏，如图4所示，被包含的框处于不同的位置时，得到的GIoU Loss与IoU Loss是一样的，无法进一步反映回归情况。且GIOU Loss在优化过程中，先减小两框之间的闭包，再增大两框之间的IoU，收敛过程较慢。

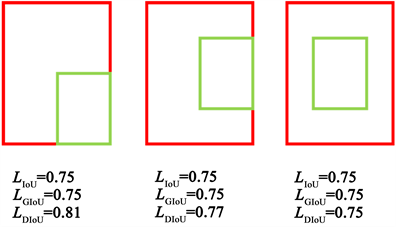
Figure 4. The instances of GIoU unable to regression

图4. GIoU无法回归示例

为了解决上述问题，DIoU Loss提出将GIoU Loss中的惩罚项改为 $R=\frac{{\rho }^2}{c^2}$，如图5所示：

Figure 5. DIoU schematic diagram of penalty items

图5. DIoU惩罚项示意图

其中 ${\rho }^2$ 表示两个矩形框的中心点的欧氏距离， $c^2$ 表示两个矩形框的最小闭包的对角线平方。DIoU Loss由公式(14)定义：

$L_{\text{DIoU}}=1-\text{IoU}+\frac{{\rho }^2}{c^2}$ (14)

由图3可知，DIoU能够反映两框之间的位置关系，并且DIoU loss可以直接拉进两个目标框的距离，同时增大两框之间的IoU，加快收敛速度。

3.2.4. CIoU Loss

CIoU Loss认为候选框与真实框进行匹配的几何要素包括面积、中心点距离、长宽比例，这三部分决定了候选框的定位精确度。DIoU Loss已经包含了面积与中心点距离，因此CIoU Loss将两框的长宽比也作为惩罚项加入损失函数中，如公式(15)所示：

$L_{\text{CIoU}}=1-\text{IoU}+\frac{{\rho }^2}{c^2}+\alpha v$ (15)

其中权衡参数 $\alpha =\frac{v}{1-\text{IoU}+v}$ 用于控制长宽比的系数，而 $v=\frac{4}{{\pi }^2}{\left({\tan }^{-1}\frac{w^G}{h^G}-{\tan }^{-1}\frac{w^P}{h^P}\right)}^2$ 则用于描述两框的比例一致性。

3.2.5. Focal EIoU Loss

当两个矩形框的长度和宽度呈倍数关系时，长宽比相等但大小不等，此时CIoU Loss中 $\alpha v$ 失效。并

且通过求导发现 $\frac{\partial v}{\partial w}=-\frac{h}{w}\cdot \frac{\partial v}{\partial h}$，宽和高的梯度方向相反，即当宽和高其中一个变量增大时，另一个变量

必然减小，不能做到同增同减。因此设计EIoU Loss，将长和宽分别进行优化，函数定义如公式(16)所示：

$L_{\text{EIoU}}=1-\text{IoU}+\frac{{\rho }^2}{c^2}+\frac{{\rho }^2\left(w,w^{gt}\right)}{C_w^2}+\frac{{\rho }^2\left(h,h^{gt}\right)}{C_h^2}$ (16)

其中 $C_w^2$ 和 $C_h^2$ 分别为两个矩形框最小闭包的宽和高。

分类任务提高难分类样本有助于模型收敛，回归任务则是提高易分类样本有助于模型收敛。因此为了提高候选框回归的准确度，EIoU Loss借鉴Focal Loss的思想，提高易分类样本在损失函数中所占比重，提出Focal EIoU Loss，函数定义如公式(17)所示：

$L_{\text{FocalEIoU}}={\text{IoU}}^{\gamma }{L}_{\text{EIoU}}$ (17)

4. 总结与展望

本文对目标检测中的损失函数从分类损失与回归损失两方面进行了详尽的介绍，并分析了各个损失函数的优缺点。尽管目标检测已经得到了快速发展发展地较为成熟，但是仍旧不能满足现实中的应用需求，因此仍需从各个模块进行改进。其中损失函数的优化是必不可少的，现有IoU损失函数仍有可优化的内容。此外，在目标遮挡问题、小目标检测等领域中，损失函数亟需更大的优化。

基金项目

国家自然科学基金(No. 62072024)；北京建筑大学北京未来城市设计高精尖创新中心资助项目(UDC2017033322，UDC2019033324)；北京建筑大学市属高校基本科研业务费专项资金资助(NO. X20084，ZF17061)。