量子电池中量子失协的作用

The Role of Quantum Discord in Quantum Battery

摘要: 在本文中，我们用一个两量子比特系统模拟了量子电池–充电器模型，通过精确求解两个全同二能级原子共处于一个单模腔场系统中，讨论了在不同平均光子数下量子失协对量子电池中能量转换和最大功的影响。研究表明：量子失协提供了量子电池系统中低能量向高能量传输的动力，并且最大功会随着光子数的增加而变化。当光子数较小时，系统内的演化受量子失协影响较大，随着光子数的增加，光子数在演化中所占权重越来越大，导致系统的演化更加复杂。

Abstract: In this paper, we use a two-qubit system to simulate the quantum battery charger model. By accu-rately solving that two identical two-level atoms are in a single-mode cavity field system, the effects of quantum discord on energy conversion and ergotropy in the quantum battery under different average photon numbers are discussed. The results show that the quantum discord provides the power for the transmission of low energy to high energy in the quantum battery system, and the ergotropy will change with the increase of the number of photons. When the number of photons is small, the evolution of the system is greatly affected by quantum discord. With the increase of the number of photons, the weight of the number of photons in the evolution becomes larger and larger, resulting in a more complex evolution of the system.

1. 引言

量子关联 [1] 作为量子信息中的重要资源，直接影响量子信息处理的效率与可靠性，它被广泛地应用于量子通信和量子计算。量子纠缠 [2] [3] 作为量子关联的一种，是量子力学特有的一个重要性质，描述了存在于量子系统之间的超越经典的关联。在很长一段时间里，人们一直认为纠缠是唯一一种量子关联，因此量子关联一度只停留在对纠缠问题的研究上。但实验和理论证实了量子纠缠不包括所有的量子关联，为更加全面描述量子关联，Ollivier和Zurek在2001年提出量子失协(quantum discord，简记为QD) [4]，并发现量子失协对量子关联的描述比量子纠缠更具有普遍性和优越性。研究发现，量子失协除了能够提高计算速度 [5] [6]，还能够应用于远程态制备 [7] [8]、量子密钥分配 [9] 及量子密码 [10] 等量子信息处理任务 [11]。量子失协不仅是一种信息资源，也是一种物理资源，这是由于量子关联发生变化必然伴随着系统和环境的熵的产生。

在量子热力学领域内，量子电池 [12] 系统作为用于临时储能并从充电器转移到电池的量子系统，近些年引起了人们的广泛关注。Tabesh等 [13] 研究了普通耗散玻色子环境中量子电池的最大功，考虑了非马尔可夫和马尔可夫环境下随时间演化的共同环境介导的双量子位动力学。结果表明，欠阻尼状态和/或强外场可以在马尔可夫环境下开放量子电池最佳充电过程中发挥重要作用。Kamin等 [14] 的研究表明由非马尔可夫环境引起的记忆效应有利于量子电池的充电过程，并且，记忆效应可以显著提高量子电池的性能。Caravelli等 [15] 研究了相干性在封闭环境下和开放环境下对量子电池中的作用，得到了关于相干性的封闭环境中量子电池和开放环境中量子电池的最大功和能量交换的上界。具体地说，证明了量子电池演化的中的能量存储可以被相干性所限制。在上述研究的启发下，本文主要讨论了在不同平均光子数下量子失协对量子电池中能量转换和最大功的影响。

2. 理论描述

为清楚起见，首先我们对投影测量下的量子失协和理论模型进行简要介绍。

2.1. 量子失协

在经典信息论中，如果对一个系统a的某个随机变量进行测量，测得的概率分布为 $p_j^a$，j为被测量

的随机变量，那么这个随机变量的平均信息量可以由Shannon熵 $H\left(a\right)=-{\displaystyle \underset{j}{\sum }{p}_j^a\log p_j^a}$ 来表示，两个经典

系统a和b之间的全关联可以表示为：

$I\left(a:b\right)=H\left(a\right)+H\left(b\right)-H\left(a,b\right)$ (1)

其中对系统a和b进行同时测量获得的概率分布用一个联合分布函数 $p_{jk}^{ab}$ 表示，利用Bayes公式可以得到其等价表达：

$J\left(a,b\right)=H\left(a\right)-H\left(a|b\right)=H\left(b\right)-H\left(b|a\right)$ (2)

其中 $H\left(a|b\right)={\displaystyle \underset{jk}{\sum }{p}_{jk}^{ab}\log p_{j|k}^{a|b}}$ 称为条件熵， $p_{j|k}^{a|b}=\frac{p_{jk}^{ab}}{p_k^b}$ 表示在给定系统b测量结果下，系统a的测量概率

分布，被称为条件概率。

将经典互信息的概念推广到量子系统中，即用Von Neumann熵代替Shannon熵，则：

$I\left({\rho }_{ab}\right)=S\left({\rho }_a\right)+S\left({\rho }_b\right)-S\left({\rho }_{ab}\right)=S\left({\rho }_a\right)-S\left(a|b\right)$ (3)

其中， $S\left({\rho }_j\right)=-Tr\left({\rho }_j{\log }_2{\rho }_j\right)=-{\displaystyle {\sum }_i{\lambda }_j^i{\log }_2{\lambda }_j^i}$ 为Von Neumann熵，下标j表示子系统a(b)或者整个系统ab， ${\rho }_a$ 和 ${\rho }_b$ 是 ${\rho }_{ab}$ 的约化密度矩阵， $\left\{{\lambda }_j^i\right\}$ 是量子态 ${\rho }_j$ 的非零本征值； $S\left(a|b\right)=S\left({\rho }_{ab}\right)-S\left({\rho }_b\right)$ 表示测量第二个子系统时第一个子系统的条件熵。

给定一个具有简化系统状态的二量子比特态，标准量子失协被定义为互信息和经典关联之间的差，如下式所示：

$D\left({\rho }_{ab}\right)=I\left({\rho }_{ab}\right)-C^{\prime }\left({\rho }_{ab}\right)$ (4)

其中 $C^{\prime }\left({\rho }_{ab}\right)$ 是经典关联，被定义为：

$C^{\prime }\left({\rho }_{ab}\right)=S\left({\rho }_a\right)-\underset{\left\{{\Pi }_k\right\}}{\min }\left[S\left({\rho }_{ab}|\left\{{\Pi }_k\right\}\right)\right]$ (5)

其中最小值取自投影测量的完备集 $\left\{{\Pi }_k\right\}$， $S\left({\rho }_{ab}|\left\{{\Pi }_k\right\}\right)={\displaystyle {\sum }_k{p}_{k}S\left({\rho }_k\right)}$ 是子系统a在给定子系统b上完备集的量子条件熵，并且有 ${\rho }_k=T{r}_b\left({\Pi }_k{\rho }_{ab}{\Pi }_k\right)/p_k$， $p_k=T{r}_{ab}\left({\rho }_{ab}{\Pi }_k\right)$。因此，量子失协 [16] 可以表示为：

$D\left({\rho }_{ab}\right)=S\left({\rho }_b\right)-S\left({\rho }_{ab}\right)+\underset{\left\{{\Pi }_k\right\}}{\min }S\left({\rho }_{ab}|\left\{{\Pi }_k\right\}\right)$ (6)

2.2. 理论模型

我们用一个两量子比特系统模拟了量子电池–充电器模型：两个全同二能级原子共处于一个单模腔场内，并且忽略两个原子之间的相互作用，而只考虑两个原子和腔场的各自的相互作用。每个电池单元被建模为一个具有激发态 $|1\rangle$ 和基态 $|0\rangle$ 的两能级系统，我们假设两个量子位具有相同的跃迁频率， ${\omega }_A={\omega }_B=\omega$，并且光场的频率等于原子的跃迁频率 $\omega =\nu$。在旋波近似(RWA)下，系统的总哈密顿量描述如下(其中为 $\hslash =1$ )：

$H=H_0+H_1$ (7)

$H_0=\frac{1}{2}\omega {\sigma }_z^A+\frac{1}{2}\omega {\sigma }_z^B+\nu a^{+}a$ (8)

$H_1=g{\mu }_1\left(a^{+}{\sigma }_{-}^A+a{\sigma }_{+}^A\right)+g{\mu }_2\left(a^{+}{\sigma }_{-}^B+a{\sigma }_{+}^B\right)$ (9)

其中 ${\sigma }_z^A$ 和 ${\sigma }_z^B$ 分别是原子A和B的反转算符， $a^{+}$ 和a分别是储层中相应腔场光子的产生(湮灭)算符。 $H_1$ 描述的是系统与储层之间的相互作用， ${\sigma }_{-}^A$ 和 ${\sigma }_{+}^A$ 分别为原子A的下降算符、上升算符， ${\sigma }_{-}^B$ 和 ${\sigma }_{+}^B$ 分别为原子B的下降算符、上升算符。g为原子与腔场间的耦合常数， ${\mu }_1$ 和 ${\mu }_2$ 是无量纲实参数。

如果 $\rho \left(t\right)$ 是原子–场系统在t时刻的密度算符，那么系统演化由量子刘维方程给出：

$\frac{\text{d}\rho \left(t\right)}{\text{d}t}=-\frac{i}{\hslash }\left[H_I,\rho \left(t\right)\right]$ (10)

其中 $H_I$ 是相互作用哈密顿量，上述方程的等价表示可以写为：

$\rho \left(t\right)=U\rho \left(0\right)U^{+}$ (11)

其中总系统的幺正时间演化算符可以写为：

$\begin{array}{c}U=\exp \left(-i{H}_{I}t/\hslash \right)\\ =\exp \left[-i\lambda t\left(a{\sigma }_{+}^A+a^{+}{\sigma }_{-}^A\right)\right]\otimes \exp \left[-i\lambda t\left(a{\sigma }_{+}^B+a^{+}{\sigma }_{-}^B\right)\right]\\ =U_A\otimes U_B\end{array}$ (12)

其中 $U_A=\exp \left[-i\lambda t\left(a{\sigma }_{+}^A+a^{+}{\sigma }_{-}^A\right)\right]$， $U_B=\exp \left[-i\lambda t\left(a{\sigma }_{+}^B+a^{+}{\sigma }_{-}^B\right)\right]$ 分别是子系统A、B的幺正时间演化算符，总系统的幺正时间演化算符的转置共轭为：

$U^{+}=U_B^{+}\otimes U_A^{+}$ (13)

若选择初始态 $\rho \left(0\right)=r|{\psi }_0\rangle \langle {\psi }_0|+\frac{1-r}{4}I$， $|{\psi }_0\rangle =\cos \theta |e_A{g}_B\rangle +\sin \theta |g_A{e}_B\rangle$ 代入量子刘维方程，解得：

$\rho \left(t\right)=\left(\begin{array}{cccc}{\rho }_{11}& 0& 0& {\rho }_{14}\\ 0& {\rho }_{22}& {\rho }_{23}& 0\\ 0& {\rho }_{32}& {\rho }_{33}& 0\\ {\rho }_{41}& 0& 0& {\rho }_{44}\end{array}\right)$ (14)

使用此密度矩阵，可以直接获得量子电池系统中充电器和电池的内能，即 $E_{A/B}\left(t\right)=tr\left[\rho {\left(t\right)}_{A/B}{H}_{A/B}\right]$，使用以上密度矩阵，我们有 $E_A\left(t\right)={\omega }_0\left({\rho }_{11}+{\rho }_{22}\right)$， $E_B\left(t\right)={\omega }_0\left({\rho }_{11}+{\rho }_{33}\right)$。

为了表征在循环幺正操作下，在充电过程结束时可以从量子电池中提取的最大能量，引入最大功 [17] [18]：

$W\left(\tau \right)=Tr\left({\rho }_B\left(\tau \right)H_B\right)-Tr\left({\sigma }_{\rho B}{H}_B\right)$ (15)

其中 $H_B$ 和 ${\rho }_B$ 分别为电池的哈密顿量和状态。循环幺正演化操作中 ${\rho }_B$ 的可提取能量为零时，此时， ${\sigma }_{\rho B}$ 被称为 ${\rho }_B$ 的被动态。

根据公式(14)和(15)，最大功变为

$W\left(\tau \right)={\omega }_0\left(2\left({\rho }_{11}+{\rho }_{33}\right)-1\right)\Theta \left(\left({\rho }_{11}+{\rho }_{33}\right)-\frac{1}{2}\right)$ (16)

其中 $\Theta \left(x-x_0\right)$ 是Heaviside函数。在这里我们有 $W_{\max }={\omega }_0$。

将公式(14)代入量子失协公式(6)，通过改变平均光子数，可以得出量子电池中量子失协的动力学演化图像。

3. 分析与讨论

为了研究量子失协在量子电池中对能量转换和最大功的影响，我们将通过改变平均光子数绘制成标度时间 $\gamma t$ 的函数进行分析：

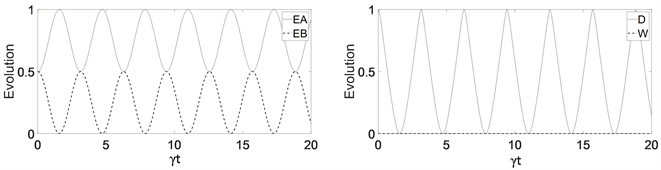
图1(a)是平均光子数 $n={10}^{-5}$ 时充电器能量(E_a)和电池能量(E_b)随 $\gamma t$ 的动力学演化图像，图1(b)是量子失协(QD)和最大功(W)随 $\gamma t$ 的动力学演化图像。我们可以看出光子数很小时， $W=0$，这是因为电池E_b的能量一直小于充电器E_a的能量，量子电池系统几乎没有对外做功的能力，所以最大功 $W=0$。而之所以电量较低电池可以给电量较高的充电器进行充电，这是因为当光子数很小时，量子电池系统的动力学演化只与量子关联有关。由于初始时刻 $E_a=E_b$，电量相等，不存在电势差，此时的E_a与E_b之间的能量交换完全由量子关联(本文研究的量子关联为量子失协)作为动力。根据图1可以看出，随着较小的E_b给较大的E_a充电的进行，D不断减小，而当E_a达到最大值1，E_b达到最小值0， $D=0$，这说明当量子关联完全耗尽时，系统有低电量向高电量充电的能力也不复存在。此时，由于充电器与电池之间电势差的存在，高电量的E_a自发地向低电量的E_b进行充电，而随着充电的进行，量子电池系统内的量子关联也逐渐回复，D不断上升。

(a) (b)

Figure 1. Average photon number $n={10}^{-5}$ : (a) Evolution curve of charger energy (solid line) and battery energy (dotted line); (b) Evolution curves of quantum discord D (solid line) and ergotropy W (dotted line)

图1. 平均光子数 $n={10}^{-5}$ 时：(a) 充电器能量(实线)、电池能量(虚线)演化曲线；(b) 量子失协D (实线)、最大功W (虚线)的演化曲线

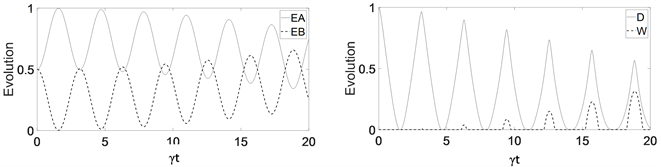
图2(a)是平均光子数 $n={10}^{-3}$ 的充电器能量(E_a)和电池能量(E_b)随 $\gamma t$ 的动力学演化图像，图2(b)是量子失协(QD)和最大功(W)随 $\gamma t$ 的动力学演化图像。随着平均光子数的增加，在 $E_b>E_a$ 的区间内，存在W，这是因为最大功W是量子电池系统可以输出的最大能量；当 $E_a>E_b$ 时，量子电池系统并不能对外做功。可以看出，随着演化的进行，D可以取得的最大值越来越小，这是因为当光子数增大时，系统的演化不仅由量子关联和电势差决定，还应考虑光子的作用。当系统刚开始演化时， $E_a-E_b=0$， $D=1$，此时系统的演化如同图1，但随着演化的进行，由于光子数的增多，电池具有了对外做功的能力，导致可供D与E_a、E_b间的转化的能量越来越少，所以D可取得的最大值越来越小，E_a与E_b的交集越来越大，上限越来越低，W可取得的最大值越来越大。

(a) (b)

Figure 2. Average photon number $n={10}^{-3}$ : (a) Evolution curve of charger energy (solid line) and battery energy (dotted line); (b) Evolution curves of quantum discord D (solid line) and ergotropy W (dotted line)

图2. 平均光子数 $n={10}^{-3}$ 时：(a) 充电器能量(实线)、电池能量(虚线)演化曲线；(b) 量子失协D (实线)、最大功W (虚线)的演化曲线

图3(a)是平均光子数 $n=0.1$ 的充电器能量(E_a)和电池能量(E_b)随 $\gamma t$ 的动力学演化图像，图3(b)是量子失协(QD)和最大功(W)随 $\gamma t$ 的动力学演化图像。当光子数进一步增大时，可以看出，从初始时刻的演化，E_a与E_b在第一个波峰已经不能达到它们可以取得的最大值，这是因为此时光子数的作用在演化中的权重进一步上升，在第一个波峰内就已经使D与E_a、E_b间的转化中的相当一部分能量变为W。

(a) (b)

Figure 3. Average photon number n = 0.1: (a) Evolution curve of charger energy (solid line) and battery energy (dotted line); (b) Evolution curves of quantum discord D (solid line) and ergotropy W (dotted line)

图3. 平均光子数n = 0.1时：(a) 充电器能量(实线)、电池能量(虚线)演化曲线。(b) 量子失协D (实线)、最大功W (虚线)的演化曲线。

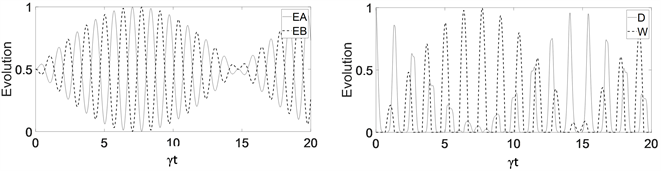
图4(a)是平均光子数 $n=5$ 的充电器能量(E_a)和电池能量(E_b)随 $\gamma t$ 的动力学演化图像，图4(b)是量子失协(QD)和最大功(W)随 $\gamma t$ 的动力学演化图像。当光子数很大时，在系统刚开始演化时，就有很多的光子参与其中，导致E_a、E_b可以恢复的是周期内的最小值，这是因为，量子失协所提供的由低能量向高能量传输的动力几乎都变成了系统对外做功的能力。而由于转化回的量子失协越来越少，参与其中的光子数作用也越来越低，导致可供恢复的E_a、E_b越来越大，此时( $t=8$ 左右)系统的演化以E_a、E_b、W之间的转化为主。但由于参与其中的光子数减少，量子失协恢复的能力增强，此时系统的演化开始向可恢复的失协越来越多，E_a、E_b、W的最大值越来越小的方向变化。

(a) (b)

Figure 4. Average photon number $n=5$ : (a) Evolution curve of charger energy (solid line) and battery energy (dotted line); (b) Evolution curves of quantum discord D (solid line) and ergotropy W (dotted line)

图4. 平均光子数 $n=5$ 时：(a) 充电器能量(实线)、电池能量(虚线)演化曲线；(b) 量子失协D (实线)、最大功W (虚线)的演化曲线

4. 结论

在本文中，我们将量子电池模型描述为双量子位系统，研究了在不同平均光子数下量子失协对量子电池中能量转换和最大功的影响。从结果可以看出，量子失协是低能力量向高能量充电的动力。光子数很小时，系统几乎没有对外做功的能力，随着平均光子数的增加，电池对外做功的能力越来越强，但是对外做功的能力越强，量子失协对电池电量之间转化的影响就越弱。

NOTES

^*通讯作者。