一个(2 + 1)-维KdV方程的lump解与lump-stripe 混合解

Lump Solutions and Mixed Lump-Stripe Solutions of a (2 + 1)-Dimensional KdV Equation

摘要: 本文通过利用Hirota双线性形式，并借助Maple符号计算，得到了(2 + 1)-维KdV方程的lump解、lump-stripe混合解。通过选取不同的参数，并结合图像研究了这些解的动力学特征，特别是讨论了lump解和stripe解之间的相互作用现象。这些解及其相关的性质将有助于研究(2 + 1)-维KdV方程所描述的物理学现象。

Abstract: In this paper, by using Hirota bilinear form, the lumped solution and lump strip mixed solution of (2 + 1)-dimensional KdV equation are obtained with the help of Maple symbolic calculation in this paper. By choosing different parameters, the dynamic characteristics of these solutions are studied combined with images, especially the interaction between lumps and stripe solutions. These solutions and their related properties will help to study the dynamic characteristics described by physical phenomena of the (2 + 1)-dimensional KdV equation.

1. 引言

众所周知，非线性发展方程的精确解在孤立子理论的发展中起着举足轻重的作用。在寻求孤子方程精确解的过程中，Horita双线性方法 [1] 是一个重要而直接的方法。Hirota双线性算子定义为

$D_t^m{D}_x^n\left(f\cdot f\right)=D_t^m{D}_x^n\left(f\left(t,x,y\right)f\left(t,x,y\right)\right)=\frac{{\partial }^m}{\partial T^n}\frac{{\partial }^n}{\partial T^n}\times {\left[f\left(t+T,x+X,y\right)f\left(t-T,x-X,y\right)\right]|}_{T=0,X=0}.$。

对于(2 + 1)-维KdV方程 [2]

$u_t+3u{u}_y+u_{xxy}+3u_x{\displaystyle {\int }_{-\infty }^x{u}_y\left(t,x,y\right)\text{d}x}=0$ (1)

张玉峰教授利用Hirota方法给出方程(1)的精确双孤子解，并利用适当的代数变换和Riccati方程，将Riccati方程中的变量作为自变量，得到了方程(1)的一类钟形孤子解。冯滨鲁 [3] 则利用Pfaffianization方法推导出方程(1)的耦合系统及其Gramm型的pfaffian解。

近年来，lump解的研究受到众多国内外学者的关注。2015年，马文秀教授 [4] 利用双线性方法并通过Maple进行符号计算，得到了(2 + 1)维Kadomtsev-Petviashvili (KP)方程的一类在各个方向上合理局部化的lump解，并分析了其动力学行为。2017年，赵等 [5] 利用(2 + 1)维非对称Nizhnik-Novikov-Veselov方程的双线性形式，得到了该方程的lump解、stripe解以及lump周期解，并讨论了lump解与stripe解之间的相互作用，证明了两个孤立波之间的相互作用是非弹性的。2018年，陈守婷等 [6] [7] 利用双线性方法并借助Maple符号计算研究了广义Bogoyavlensky-Konopelchenko方程及广义(2 + 1)-维Calogero-Bogoyavlenskii-Schiff方程的lump解，并通过图像分析了lump解的动力学特征。2020年，张玉峰教授等 [8] 利用双线性方法和符号计算研究了广义(2 + 1)-维Hirota-Satsuma-Ito方程的lump解，并分析了解的动力学特征。

本文在前面学者研究的基础上，利用Horita双线性方法，利用符号计算，讨论张玉峰教授所构造的(2 + 1)-维KdV方程(1)的lump解与lump-stripe混合解，并分析其动力学特征。

2. (2 + 1)-维KdV方程的lump解与lump-stripe解

首先假设 $f=f\left(x,y,t\right)$ 是关于变量 $x,y,t$ 的可微函数，作变量代换 $u=u_0+2{\left(\ln f\right)}_{xx}$ 代入方程(1)，可得

$2{\left(\ln f\right)}_{xxt}+6\left[u_0+2{\left(\ln f\right)}_{xx}\right]{\left(\ln f\right)}_{xxy}+2{\left(\ln f\right)}_{xxxxy}+12{\left(\ln f\right)}_{xxx}{\left(\ln f\right)}_{xy}=0.$ (2)

对变量x进行一次积分，可得方程(1)的双线性导数方程为

$D_x\left(D_t+3u_0{D}_y+D_x^2{D}_y\right)\left(f\cdot f\right)=0.$ (3)

为得到方程(1)的lump-stripe解，可设

$f=g^2+h^2+k_1{\text{e}}^{\left(k_{2}x+k_{3}y+k_{4}t\right)}+a_9$ (4)

上式中， $g=a_{1}x+a_{2}y+a_{3}t+a_4$， $h=a_{5}x+a_{6}y+a_{7}t+a_8$，其中 $a_j\left(1\le j\le 9\right)$ 和 $k_j\left(1\le j\le 4\right)$ 均是待定的实数参数。将式(4)代入式(3)，借助符号计算软件Maple，搜集关于变量 $x,y,t$ 及 ${\text{e}}^{\left(k_{2}x+k_{3}y+k_{4}t\right)}$ 的系数，就会得到关于待定系数 $a_j$ 和 $k_j$ 的多项式方程。通过求解这些方程， $a_j\left(1\le j\le 9\right)$ 和 $k_j\left(1\le j\le 4\right)$ 就会被随之确定。我们讨论下面两种情形：

(1) 当 $k_1=0$ 时，可以得到方程(1)的若干种不同形式的lump解。在此，只讨论其中的一种：

$a_1=a_1,a_2=0,a_3=0,a_4=a_4,a_5=0,a_6=a_6,a_7=a_7,a_8=a_8,a_9=a_9,u_0=-\frac{a_7}{3a_6}.$ (5)

这样得到双线性导数方程(3)的解为

$f={\left(a_{1}x+a_4\right)}^2+{\left(a_{6}y+a_{7}t+a_8\right)}^2+a_9.$ (6)

式中 $a_1,a_4,a_7,a_8,a_9$ 为任意实数，且 $a_6$ 是非零实数。通过变换 $u=u_0+2{\left(\ln f\right)}_{xx}$ 可得方程(1)的lump解为

$u=u_0+\frac{4a_1^{2}f-8a_1^2{g}^2}{f^2}.$ (7)

上式中， $g=a_{1}x+a_4$， $u_0$，f与上述表示形式相同。

下面讨论解(7)的相关性质。首先假设时间t是常量，取 $\{\begin{array}{l}{u}_x=0\\ u_y=0\end{array}$ 可得到一个驻点

$\left(x_1,y_1\right)=\left(-\frac{a_4}{a_1},-\frac{a_{7}t+a_8}{a_6}\right)$。

经过计算，在驻点 $\left(x_1,y_1\right)$ 处的Hessian矩阵

$\Delta ={\left|\begin{array}{cc}\frac{{\partial }^{2}u}{\partial x^2}& \frac{{\partial }^{2}u}{\partial x\partial y}\\ \frac{{\partial }^{2}u}{\partial x\partial y}& \frac{{\partial }^{2}u}{\partial y^2}\end{array}\right|}_{\left(-\frac{a_4}{a_1},-\frac{a_{7}t+a_8}{a_6}\right)}=\frac{192a_1^6{a}_6^2}{a_9^4}>0.$ (8)

且 $u_{xx}\left(x_1,y_1\right)=-\frac{24a_1^4}{a_9^2}<0$，因此式(7)在 $\left(x_1,y_1\right)$ 处得到最大值，且最大值为 $-\frac{a_7}{3a_6}+\frac{4a_1^2}{a_9}$。当参数

$a_1=1,a_4=1,a_6=-1,a_7=2,a_8=1,a_9=2$ 时，式(7)的lump解的在 $t=-3,t=0,t=3$ 三个不同时刻的三维图和密度图如图所示：

从图1可以看出，在不同时刻，lump孤子的结构没有发生改变，只是位置发生了移动。

(2) 当 $k_1\ne 0$ 时，下面讨论双线性方程(3)的四种lump-stripe解。

解一：

$\begin{array}{l}{k}_1=k_1,k_2=0,k_3=k_3,k_4=0,a_1=0,a_2=a_2,a_3=0,\\ a_4=a_4,a_5=a_5,a_6=0,a_7=0,a_8=a_8,a_9=a_9,u_0=0.\end{array}$

Figure 1. Three dimensional diagrams and density diagrams of equation (7) at different times

图1. 式(7)在不同时刻的三维图和密度图

这样，我们可以得到双线性方程(3)的含有二次函数及指数函数形式的解为

$f={\left(a_{2}y+a_4\right)}^2+{\left(a_{5}x+a_8\right)}^2+k_1{\text{e}}^{k_{3}y}+a_9.$ (9)

上式中 $k_1,k_3,a_2,a_4,a_5,a_8,a_9$ 为任意常数。将(9)代入 $u=u_0+2{\left(\ln f\right)}_{xx}$ 可得方程(1)的lump-stripe混合解。如果取

$k_1=1,k_3=1,a_2=1,a_4=2,a_5=1,a_8=1,a_9=2,u_0=0$

可以得到(1)的lump-stripe混合解

$u=\frac{4}{{\left(y+2\right)}^2+{\left(x+1\right)}^2+{\text{e}}^y+2}-\frac{8{\left(x+1\right)}^2}{{\left({\left(y+2\right)}^2+{\left(x+1\right)}^2+{\text{e}}^y+2\right)}^2}.$ (10)

式(10)的三维图与密度图如图2所示。因为上式中不显含时间t，故从图2中可以看出，本次得到的孤子作用结构，随时间变化不会发生变化。

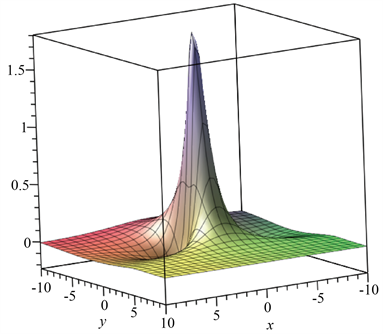
Figure 2. Three dimensional diagrams and density diagrams of equation (10)

图2. 式(10)的三维图和密度图

解二：

$\begin{array}{l}{k}_1=k_1,k_2=0,k_3=k_3,k_4=k_4,a_1=0,a_2=\frac{k_3{a}_3}{k_4},a_3=a_3,\\ a_4=a_4,a_5=a_5,a_6=0,a_7=0,a_8=a_8,a_9=a_9,u_0=-\frac{k_4}{3k_3}.\end{array}$

这样，我们可以得到双线性方程(3)的含有二次函数及指数函数形式的解为

$f={\left(\frac{k_3{a}_3}{k_4}y+a_{3}t+a_4\right)}^2+{\left(a_{5}x+a_8\right)}^2+k_1{\text{e}}^{k_{3}y+k_{4}t}+a_9.$ (11)

上式中 $k_1,k_3,k_4,a_3,a_4,a_5,a_8,a_9$ 为任意常数。将(11)代入 $u=u_0+2{\left(\ln f\right)}_{xx}$ 可得到方程(1)的lump-stripe混合解。如果取

$k_1=1,k_3=1,k_4=2,a_3=1,a_4=2,a_5=1,a_8=1,a_9=2$

可以得到(1)的lump-stripe混合解

$u=-\frac{2}{3}+\frac{4}{{\left(0.5y+t+2\right)}^2+{\left(x+1\right)}^2+{\text{e}}^{y+2t}+2}-\frac{8{\left(x+1\right)}^2}{{\left({\left(0.5y+t+2\right)}^2+{\left(x+1\right)}^2+{\text{e}}^{y+2t}+2\right)}^2}.$ (12)

式(12)的lump-stripe解在 $t=-2,t=0,t=2$ 三个不同时刻的三维图和密度图如图3所示。在式(12)中，当 $t\to \infty$， $u\to 0$。也就是说，随着时间的变化增大，lump-stripe对应的水波会消失。并且从图3中可以看出，lump与stripe孤子发生弹性碰撞时，lump孤子吞噬了stripe孤子，使lump孤子形状发生了改变。

解三：

$\begin{array}{l}{k}_1=k_1,k_2=0,k_3=k_3,k_4=k_4,a_1=a_1,a_2=-\frac{a_5{a}_6}{a_1},a_3=-\frac{k_4{a}_5{a}_6}{k_3{a}_1},\\ a_4=a_4,a_5=a_5,a_6=a_6,a_7=\frac{k_4{a}_6}{k_3},a_8=a_8,a_9=a_9,u_0=-\frac{k_4}{3k_3}.\end{array}$

Figure 3. Three dimensional diagrams and density diagrams of equation (12) at different times

图3. 式(12)在不同时刻的三维图和密度图

这样，我们可以得到双线性方程(3)的含有二次函数及指数函数形式的解为

$f={\left(a_{1}x--\frac{a_5{a}_6}{a_1}y-\frac{k_4{a}_5{a}_6}{k_3{a}_1}t+a_4\right)}^2+{\left(a_{5}x+a_{6}y+\frac{k_4{a}_6}{k_3}t+a_8\right)}^2+k_1{\text{e}}^{k_{3}y+k_{4}t}+a_9.$ (13)

上式中 $k_1,k_3,k_4,a_1,a_4,a_5,a_6,a_8,a_9$ 为任意常数。将(13)代入 $u=u_0+2{\left(\ln f\right)}_{xx}$ 可得到方程(1)的lump-stripe混合解。如果取

$k_1=1,k_3=2,k_4=-1,a_1=2,a_4=1,a_5=1,a_6=2,a_8=1,a_9=1$

可以得到(1)的lump-stripe混合解

$\begin{array}{c}u=\frac{1}{6}+\frac{20}{{\left(2x-y+0.5t+1\right)}^2+{\left(x+2y-t+1\right)}^2+{\text{e}}^{2y-t}+1}\\ -\frac{8{\left(5x+3\right)}^2}{{\left({\left(2x-y+0.5t+1\right)}^2+{\left(x+2y-t+1\right)}^2+{\text{e}}^{2y-t}+1\right)}^2}.\end{array}$ (14)

式(14)的lump-stripe解在 $t=-4,t=0,t=4$ 三个不同时刻的三维图和密度图如图4所示。在式(12)中，当 ${\left(2x-y+0.5t+1\right)}^2+{\left(x+2y-t+1\right)}^2\to \infty$， $u\to 0$。并且从图4中可以看出，lump与stripe孤子发生弹性碰撞时，lump孤子吞噬了stripe孤子，使lump孤子形状发生了改变。

解四：

$\begin{array}{l}{a}_1=0,a_2=0,a_3=0,a_4=a_4,a_5=0,a_6=a_6,a_7=a_7,a_8=a_8,\\ a_9=a_9,k_1=k_1,k_2=k_2,k_3=k_3,k_4=\frac{a_7{k}_3}{a_6},u_0=-\frac{a_6{k}_2^2+a_7}{3a_6}.\end{array}$

这样，我们可以得到双线性方程(3)的含有二次函数及指数函数形式的解为

$f=a_4^2+{\left(a_{6}y+a_{7}t+a_8\right)}^2+k_1{\text{e}}^{k_{2}x+k_{3}y+\frac{a_7{k}_3}{a_6}t}+a_9.$ (15)

Figure 4. Three dimensional diagrams and density diagrams of equation (14) at different times

图4. 式(14)在不同时刻的三维图和密度图

上式中 $a_4,a_6,a_7,a_8,a_9,k_1,k_2,k_3$ 为任意常数。将(15)代入 $u=u_0+2{\left(\ln f\right)}_{xx}$ 可得到方程(1)的lump-stripe混合解。如果取

$a_4=1,a_6=1,a_7=2,a_8=2,a_9=1,k_1=1,k_2=2,k_3=-1$

可以得到(1)的lump-stripe混合解

$u=-1+\frac{8{\text{e}}^{2x-y-2t}}{{\left(y+2t+2\right)}^2+{\text{e}}^{2x-y-2t}+2}-\frac{8{\left({\text{e}}^{2x-y-2t}\right)}^2}{{\left({\left(y+2t+2\right)}^2+{\text{e}}^{2x-y-2t}+2\right)}^2}.$ (16)

式(16)的lump-stripe解在 $t=-3,t=0,t=3$ 三个不同时刻的三维图和密度图如图5所示。在式(12)中，当 ${\left(2x-y+0.5t+1\right)}^2+{\left(x+2y-t+1\right)}^2\to \infty$， $u\to 0$。从图5中可以看出，lump与stripe孤子发生弹性碰撞时，无论时间怎么变化，lump与stripe孤子不会发生分离，并且这种作用结构随时间变化不会发生变化。

Figure 5. Three dimensional diagrams and density diagrams of equation (16) at different times

图5. 式(16)在不同时刻的三维图和密度图

此时所得解的结构与文献 [5] 中的现象不同，lump孤子与stripe孤子一直结合在一块，形状没有发生改变，只是随时间变化位置发生移动，这是一种很有趣的现象。

3. 结束语

Hirota双线性方法是求可积方程孤子解的一种非常有效的方法。本文直接利用双线性方法，借助Maple符号计算软件，得到了(2 + 1)维KdV方程的lump解及lump-stripe混合解。并且借助符号计算软件Maple将本文中获得的所有解都代入方程(1)中进行了检验。本文所得到的四种lump-stripe混合解各有特点：第一种混合解不显含时间t；第二种与第三种混合解中lump孤子与stripe孤子发生的是弹性碰撞，并且lump孤子吞噬了stripe孤子；第四种混合解中lump孤子与stripe孤子发生的是非弹性碰撞，并且lump孤子与stripe孤子一直结合在一块，形状不随时间发生改变。这些结果对于理解(2 + 1)维KdV方程所描述的物理现象具有一定的理论参考价值。另外，本文求非线性演化方程lump解及lump-stripe混合解的方法简单有效，可以推广到其它一系列的非线性偏微分方程的求解。

基金项目

河南省自然科学基金(编号：162300410075)资助项目。