传感器故障下的多四旋翼编队协同容错控制

Fault Cooperative Tolerant Control for Multiple Quadrotor Systems with Sensor Faults

摘要: 当多四旋翼直升机编队中有个体突发传感器故障时，由于个体之间的信息交互，导致故障个体及能接收到故障个体信息的无故障个体偏离理想的飞行轨迹，从而使整个编队无法保持设定的轨迹飞行。故设计一种基于动态面控制技术的分布式四旋翼直升机飞控系统，使主从式编队系统在故障未知的情况下，仍能保持预设的队形飞行，且主机能跟踪上外界参考信号。最后以Qball-X4四旋翼直升机为例，验证了所提算法的有效性。

Abstract: Due to the local communication among individuals in multiple quadrotor systems, once some quadrotors in the formation have sensor faults, the faulty quadrotors and the ones which can receive the information from them may deviate from the desired path such that the predesigned formation shape cannot be maintained. Thus, a distributed control scheme based on the dynamic surface control is proposed for multiple quadrotor systems with unknown senor faults to maintain a leader-follower formation. Moreover, the leader can always follow the external reference signals under the designed controllers. By doing simulation studies on Qball-X4 quadrotors, the results show the effectiveness of the proposed method.

1. 引言

四旋翼直升机是一种小型无人机，由于它较其他无人机有成本低廉、结构简单等优点 [1]，故广泛地运用于高危任务中，如环境监测、侦查、目标跟踪等。而多四旋翼直升机编队，即由多个相互之间有信息交互的相同或不同的四旋翼组成的群组，无疑是完成上述任务的更好的选择，因为编队能实现合理的任务分配，进而提高系统的工作效率 [2]，同时多个微小四旋翼组成的编队比一个结构复杂的大型无人机更经济。

为了使这样的多四旋翼直升机编队正常运行，需要引入协同控制的方法，其旨在利用个体间信息的局部交互设计满足系统要求的控制策略，例如使多四旋翼直升机系统同时达到目标点，跟踪外界参考信号或者在飞行过程中保持设定的队形 [3]。

关于多智能体系统的协同控制一直是近年来的研究热点，针对该问题主要有基于图论 [4] [5] [6]、基于矩阵理论及最优控制 [7] [8] 等的方法。文献 [9] 利用图论和Lyapunov函数分析了具有变拓扑结构的非线性多智能体系统的稳定性问题。而文献 [10] 则讨论了基于极限集的非线性多智能体系统的协同控制。在文献 [11] 中，利用模型预测控制方法来设计协同控制策略。

但针对故障情况下多智能体系统协同控制的研究较少。文献 [8] 分析了在有个体发生执行器故障的情况下一类线性多智能体系统的协同行为，而文献 [11] 与 [12] 则针对一类非线性智能体系统，设计了协同容错策略来处理执行器故障的情况，使得系统在故障情况下仍满足性能要求。需要特别指出的是，文献 [13] 与 [14] 则研究了存在个体传感器故障的多智能体系统容错控制问题。具体地，文献 [13] 针对一类同时存在个体传感器故障和个体执行器故障的线性多智能体系统，提出了一种基于自适应补偿和𝐻∞控制的容错控制方法，通过设计局部自适应传感器和执行器补偿器消除传感器及执行器故障对系统性能的影响。而文献 [14] 则考虑了一类存在随机干扰、传感器及执行器故障的线性主从式多智能体系统，也利用自适应控制技术解决了故障情况下的目标跟踪问题。

本文考虑主从式四旋翼直升机编队发生个体传感器故障情况下的编队队形保持问题。在此种情况下，故障四旋翼直升机会偏离理想的飞行轨迹，从而偏离其在编队中的理想相对位置点，又由于尚有其他个体会接收到故障直升机的信息，这些个体也会随之偏离理想轨迹，最后导致整个系统无法保持预先设定的理想队形。因此，本文将设计一种基于动态面控制方法的分布式协同容错控制系统，使得整个四旋翼编队在有未知传感器故障的情况下，仍能保持预设的队形飞行，且确保在整个飞行过程中，主机始终能跟踪上外界参考信号。

Figure 1. Schematic diagram for the topology of the considered leader- follower formation

图1. 主从队形的拓扑结构示意图

本文的主要结构为：第2与第3节分别介绍编队拓扑结构的基础知识与文章的问题描述，第4节具体阐述协同容错控制策略的设计，第5节着重分析系统的稳定性，最后第6节给出仿真实例，第7节总结本文的结论。

2. 基础知识

本文利用图论的基本概念来描述编队系统的拓扑结构。首先给出有向图的定义：假设有一个有向图

$\mathcal{G}\triangleq \left(\mathcal{V},\mathcal{E},\mathcal{A}\right)$，它由n个节点和m条有向弧组成，所有节点和有向弧分别组成节点集 $\mathcal{V}=\left\{1,2,\cdots ,n\right\}$ 和有向弧集 $\mathcal{E}=\left\{{\mathcal{E}}^1,\cdots ,{\mathcal{E}}^m\right\}$。其中每条有向弧都代表着2个节点之间的有向连接，例如有向弧 $\left(i,j\right)\in \mathcal{E}$ 表明节

点j能直接接收到来自节点i的信息 [6]。

接着针对节点i，定义如下形式的邻集 ${\mathcal{N}}_i$ ：

${\mathcal{N}}_i\triangleq \left\{j\in \mathcal{V}|\left(j,i\right)\in \mathcal{E}\right\}$。

同时，定义能直接接收节点i信息的节点集合 $R_i$ ：

$R_i\triangleq \left\{j\in \mathcal{V}|\left(i,j\right)\in \mathcal{E}\right\}$。

对于上述有向图 $\mathcal{G}$，有邻接矩阵 $\mathcal{A}\in R^{n\times n}$，满足如下条件：

${\mathcal{A}}_{ij}=\{\begin{array}{l}1,若\left(j,i\right)\in \mathcal{E}\hfill \\ 0,否则\hfill \end{array}$

至此，有向图的拉普拉斯矩阵L定义如下：

$L\triangleq D-\mathcal{A}$

其中， $D\triangleq diag\left\{d_i\right\},\left(i=1,\cdots ,n\right)$， $d_i$ 表示节点i的度，其表达式为 $d_i={\displaystyle {\sum }_{j=1}^N{\mathcal{A}}_{ij}}$。

根据本文研究的编队构形，即主从队形，采用有向树来描述编队的拓扑结构。有向树可以表述成一种分层的有向图，即有向图中所有节点分多层排布。在有向树中，后一层中能接收到前一层某一节点i信息的所有节点组成节点i的子节点集，反之，节点i则为这些子节点的父节点。

主从队形的编队生成的有向树有如下特点：

该有向树的第一层仅有一个节点，该节点则是整个树的主节点。同时，它也是第二层节点的父节点；

第二层包含多个节点，它们也是主节点的子节点，以此层层类推；

该有向树中，除主节点之外的所有节点有且仅有一个父节点；

为尽可能减少节点之间连接的数量，降低通讯冗余，仅父节点与子节点之间存在直接的有向连接；且同层节点之间不存在连接。

在此，以图1为例来说明以上定义的主从队形的拓扑结构。

3. 问题描述

考虑由n架四旋翼直升机组成的主从式四旋翼编队，该编队的拓扑结构可描述成小节2中定义的有向图，且系统需满足如下性能要求：

1) 每个节点i ( $i\in \mathcal{V}$ )需跟随其父节点，而主节点则需跟踪参考信号；

2) 每个节点i ( $i\in \mathcal{V}$ )需与其邻集中的每个节点j ( $j\in {\mathcal{N}}_i$ )保持预设的相对距离，该相对距离分解到惯性坐标系后，定义为 $d_{ij}\triangleq {\left[d_{ijx},d_{ijy},d_{ijz}\right]}^{\text{T}}$，如图2所示。

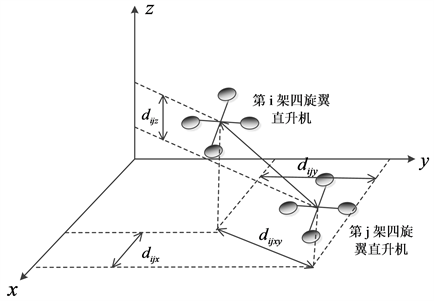
Figure 2. The relative distance between node i and node j in the inertial frame

图2. 在惯性坐标系下节点i与节点j之间的相对距离

在本文中，所有节点，即编队中的所有四旋翼直升机考虑成完全相同的个体，而节点i ( $i\in \mathcal{V}$ )的模型可建立为：

$\{\begin{array}{l}{\ddot{x}}_i=u_{i1}\left(\cos {\varphi }_i\sin {\theta }_{i}cos{\psi }_i+\sin {\varphi }_i\sin {\psi }_i\right)\\ {\ddot{y}}_i=u_{i1}\left(\cos {\varphi }_i\sin {\theta }_i\sin {\psi }_i-\sin {\varphi }_i\cos {\psi }_i\right)\\ {\ddot{z}}_i=u_{i1}\cos {\varphi }_i\cos {\theta }_i-g\\ {\ddot{\theta }}_i=u_{i2}+\frac{J_{\varphi }-J_{\psi }}{J_{\theta }}{\stackrel{\dot{}}{\psi }}_i{\stackrel{\dot{}}{\varphi }}_i\\ {\ddot{\varphi }}_i=u_{i3}+\frac{J_{\psi }-J_{\theta }}{J_{\varphi }}{\stackrel{\dot{}}{\psi }}_i{\stackrel{\dot{}}{\theta }}_i\\ {\ddot{\psi }}_i=u_{i4}+\frac{J_{\theta }-J_{\varphi }}{J_{\psi }}{\stackrel{\dot{}}{\varphi }}_i{\stackrel{\dot{}}{\theta }}_i\end{array}$ (1)

其中， $x_i,y_i,z_i$ 分别表示四旋翼重心在惯性坐标系下 $x,y,z$ 三轴上的坐标。 ${\theta }_i,{\varphi }_i,{\psi }_i$ 则分别为机体坐标系下的俯仰角、滚转角及偏航角。 $u_{i1},u_{i2},u_{i3},u_{i4}$ 为控制输入，分别代表机体坐标系下z轴上的线加速度及俯仰、滚转、偏航通道的角加速度。

为简化后续控制的设计过程，参考文献 [15]，将上述模型表述成状态空间的形式，并把该系统分解为2个子系统，如下：

一个欠驱动子系统：

$\{\begin{array}{l}{\stackrel{\dot{}}{w}}_{i1}=w_{i2}\\ {\stackrel{\dot{}}{w}}_{i2}=u_{i1}{g}_1\left(w_{i5}\right)\tau \left(w_{i3}\right)\\ {\stackrel{\dot{}}{w}}_{i3}=w_{i4}\\ {\stackrel{\dot{}}{w}}_{i4}=v_{i1}+f_{i1}\end{array}$ (2)

一个全驱动子系统：

$\{\begin{array}{l}{\stackrel{\dot{}}{w}}_{i5}=w_{i6}\\ {\stackrel{\dot{}}{w}}_{i6}=g_2\left(w_{i3}\right)v_{i2}+f_{i2}\end{array}$ (3)

其中，状态量 $w_{ik},\left(k=1,\cdots ,6\right)$ 和控制输入 $v_{ik},\left(k=1,2\right)$ 分别定义为： $w_{i1}\triangleq {\left[x_i,y_i\right]}^{\text{T}}$， $w_{i2}\triangleq {\stackrel{\dot{}}{w}}_{i1}$， $w_{i3}\triangleq {\left[{\theta }_i,{\varphi }_i\right]}^{\text{T}}$， $w_{i4}\triangleq {\stackrel{\dot{}}{w}}_{i3}$， $w_{i5}\triangleq {\left[z_i,{\psi }_i\right]}^{\text{T}}$， $w_{i6}\triangleq {\stackrel{\dot{}}{w}}_{i5}$ ； $v_{i1}\triangleq {\left[u_{i2},u_{i3}\right]}^{\text{T}}$， $v_{i2}\triangleq {\left[u_{i1},u_{i4}\right]}^{\text{T}}$。此外，根据式(1)，矩阵 $g_1,g_2$ 与向量 $f_{i1},f_{i2},\tau \left(w_{i3}\right)$ 分别为

$g_1=\frac{1}{m}\left[\begin{array}{cc}\sin {\psi }_i& \cos {\psi }_i\\ -\cos {\psi }_i& \sin {\psi }_i\end{array}\right],g_2=\left[\begin{array}{cc}\frac{\cos {\varphi }_i\cos {\theta }_i}{m}& 0\\ 0& 1\end{array}\right]$

$f_{i1}=\left[\begin{array}{c}\frac{J_{\varphi }-J_{\psi }}{J_{\theta }}{\stackrel{\dot{}}{\psi }}_i{\stackrel{\dot{}}{\varphi }}_i\\ \frac{J_{\psi }-J_{\theta }}{J_{\varphi }}{\stackrel{\dot{}}{\psi }}_i{\stackrel{\dot{}}{\theta }}_i\end{array}\right],f_{i2}=\left[\begin{array}{c}-g\\ \frac{J_{\theta }-J_{\varphi }}{J_{\psi }}{\stackrel{\dot{}}{\varphi }}_i{\stackrel{\dot{}}{\theta }}_i\end{array}\right]$

$\tau \left(w_{i3}\right)=\left[\begin{array}{c}\sin {\varphi }_i\\ \cos {\varphi }_i\sin {\theta }_i\end{array}\right]$

系统的输出 $y_{oi}\triangleq {\left[y_{oi\_1},y_{oi\_2}\right]}^{\text{T}}$ 定义为：

$\{\begin{array}{l}{y}_{oi\_1}=x_{i1}\\ y_{oi\_2}=x_{i2}\end{array}$

其中 $x_{i1}\triangleq {\left[w_{i1},w_{i3},w_{i5}\right]}^{\text{T}}$， $x_{i2}\triangleq {\left[{\stackrel{\dot{}}{w}}_{i1},{\stackrel{\dot{}}{w}}_{i3},{\stackrel{\dot{}}{w}}_{i5}\right]}^{\text{T}}$。

值得注意的是，整个编队系统中只有主机(被标记为节点1)能接收到来自外界的参考信号

$r\triangleq {\left[x_r,y_r,z_r,{\psi }_r\right]}^{\text{T}}$，其余所有僚机都无法直接获知参考信号r的信息，因此如果系统中缺少协同控制，则

所有僚机都无法沿理想轨迹飞行，从而使得整个编队系统均无法保持预设的队形飞行。

在本文中，我们考虑编队系统中有四旋翼个体的速度传感器(例如陀螺)发生故障的情况，此时将系统

中所有节点分为三部分：所有故障节点组成节点集 ${\mathcal{V}}_f$，所有直接接收故障节点信息的节点组成节点集 ${\mathcal{V}}_r$，所有剩余节点组成节点集 ${\mathcal{V}}_h$，故有 $\mathcal{V}\triangleq \left\{{\mathcal{V}}_f,{\mathcal{V}}_r,{\mathcal{V}}_h\right\}$。假设发生故障的是编队中的第i个节点，则有：

$\{\begin{array}{l}{y}_{oi\_1}=x_{i1}\\ y_{oi\_2}=x_{i2}+f_{si}\end{array}$ (4)

其中 $f_{si}=\left(k_i\left(t\right)-1\right)x_{i2}+b_i\left(t\right)$， $k_i\left(t\right)=diag\left\{k_{ij}\left(t\right)\right\}$， $b_i={\left[b_{ij}\right]}^{\text{T}}$， $j=1,\cdots ,6$。 $f_{si}$ 包含了多种传感器故障类型，当 $0<k_{ij}\left(t\right)<1$，代表第i个节点的第j个传感器发生了失效故障，表现为该传感器的读数相较于真实值成比例损失，而 $b_i\left(t\right)$ 项有

$b_i\left(t\right)=\{\begin{array}{l}{b}_i,{\stackrel{\dot{}}{b}}_i\left(t\right)\equiv 0,偏移故障\hfill \\ b_i\left(t\right),\left|b_i\left(t\right)\right|={\lambda }_{i}t,漂移故障\hfill \\ b_i\left(t\right),\left|b_i\left(t\right)\right|<{\bar{b}}_i,{\stackrel{\dot{}}{b}}_i\left(t\right)\to 0,精度损失\hfill \end{array}$

其中 $0<{\lambda }_i\le 1$， ${\bar{b}}_i>0$。偏移故障表现为传感器读数与真实值之间存在恒定偏差，漂移故障表现为两者之间的偏差随时间成比例缓慢增大，精度损失表现为两者之间的偏差在某恒定值内随时间变化，且最终趋于恒定。

对于节点i的子系统(2)与子系统(3)而言，考虑故障(4)后，其动态可等效为

$\{\begin{array}{l}{\stackrel{\dot{}}{w}}_{i1}=w_{i2}-f_{si1}\\ {\stackrel{\dot{}}{w}}_{i2}=u_{i1}{g}_1\left(w_{i5}\right)\tau \left(w_{i3}\right)\\ {\stackrel{\dot{}}{w}}_{i3}=w_{i4}-f_{si2}\\ {\stackrel{\dot{}}{w}}_{i4}=v_{i1}+f_{i1}+\delta f_{i1}\end{array}$ (5)

$\{\begin{array}{l}{\stackrel{\dot{}}{w}}_{i5}=w_{i6}-f_{si3}\\ {\stackrel{\dot{}}{w}}_{i6}=g_2\left(w_{i3}\right)v_{i2}+f_{i2}+\delta f_{i2}\end{array}$ (6)

其中 $f_{si}\triangleq {\left[f_{si1},f_{si2},f_{si3}\right]}^{\text{T}}$， $\delta f_{i1}=\delta f_{i1}\left(w_{i4},w_{i6},f_{si2},f_{si3},{\stackrel{\dot{}}{f}}_{si2}\right)$ 与 $\delta f_{i2}=\delta f_{i2}\left(w_{i4},f_{si2},{\stackrel{\dot{}}{f}}_{si3}\right)$ 为因故障导致的系统模型未知项。此时， $w_{ik}$ 可视为状态量的实际测量值。

至此，本文所要解决的问题是：针对(5)~(6)所描述的四旋翼编队，设计一种分布式协同控制策略，使得整个编队在有个体发生传感器故障的情况下仍能保持编队队形，且主机仍能跟踪上参考信号，即

${\left[x_1,y_1,z_1,{\psi }_1\right]}^{\text{T}}\to r$， ${\left[x_i-x_j,y_i-y_j,z_i-z_j\right]}^{\text{T}}\to d_{ij}$， ${\psi }_i-{\psi }_j\to 0$，其中 $j\in {\mathcal{N}}_i$。

4. 协同容错控制设计

根据四旋翼的模型特征，采用自适应动态面控制方法来实现编队系统的容错控制设计。动态面控制方法能有效地解决backstepping方法中“微分爆炸”的问题。

首先针对故障节点i (模型满足(5)~(6))设计如下形式动态面：

${\sigma }_{i1}\triangleq w_{i2}-b_i{w}_{r2}+b_i\left(w_{i1}-w_{r1}\right)+{\displaystyle \underset{j\in {\mathcal{N}}_i}{\sum }{a}_{ij}}\left(w_{i1}-w_{j1}-d_{ijxy}\right)$ (7)

${\sigma }_{i2}\triangleq w_{i3}-w_{i3d}$ (8)

${\sigma }_{i3}\triangleq w_{i4}-w_{i4d}$ (9)

${\sigma }_{i4}\triangleq w_{i6}-b_i{w}_{r6}+b_i\left(w_{i5}-w_{r5}\right)+{\displaystyle \underset{j\in {\mathcal{N}}_i}{\sum }{a}_{ij}}\left(w_{i5}-w_{j5}-h_{ij}\right)$ (10)

其中参考信号 $r\triangleq {\left[w_{r1},w_{r5}\right]}^{\text{T}}$，即 $w_{r1}\triangleq {\left[x_r,y_r\right]}^{\text{T}}$， $w_{r5}\triangleq {\left[z_r,{\psi }_r\right]}^{\text{T}}$，且 $w_{r2}\triangleq {\stackrel{\dot{}}{w}}_{r1},w_{r6}\triangleq {\stackrel{\dot{}}{w}}_{r5}$。此外， $d_{ijxy}\triangleq {\left[d_{ijx},d_{ijy}\right]}^{\text{T}},h_{ij}\triangleq {\left[d_{ijz},0\right]}^{\text{T}}$ 分别代表节点i与其邻集中的节点j之间的距离在x-y平面与z轴上的分量。

值得一提的是， $b_i$ 代表从参考信号到主机的连接权重增益，有

$b_i=\{\begin{array}{l}1,i=1,即i为主机\hfill \\ 0,i\in \mathcal{V}-\left\{1\right\},即i为僚机\hfill \end{array}$ (11)

式(9)与(10)中的 $w_{i3d},w_{i4d}$ 代表理想的俯仰角、滚转角及其角速度，其表达式通过外环信息获得，具体形式为：

$\begin{array}{c}{\stackrel{\dot{}}{w}}_{i3d}=\frac{J^{-1}\left(w_{i3d}\right)}{{\epsilon }_1}\{\frac{g_1^{-1}}{u_{i1}}\times [-k_1{\sigma }_{i1}-b_i\left(w_{i2}-{\hat{f}}_{si1}-w_{r2}\right)-{\displaystyle \underset{j\in {\mathcal{N}}_i}{\sum }{a}_{ij}}\left(w_{i2}-{\hat{f}}_{si1}-w_{j2}\right)\\ +b_i{\stackrel{\dot{}}{w}}_{r2}-{\epsilon }_1\frac{\text{d}{u}_{i1}{g}_1}{\text{d}t}\tau \left(w_{i3d}\right)]-\tau \left(w_{i3d}\right)\}\end{array}$ (12)

${\stackrel{\dot{}}{w}}_{i4d}=\frac{1}{{\epsilon }_2}\left(-k_2{\sigma }_{i3}+{\stackrel{\dot{}}{w}}_{i3d}+{\hat{f}}_{si2}-w_{i4d}\right)$ (13)

其中 $J\left(w_{i3}\right)\triangleq \frac{\partial \tau \left(w_{i3}\right)}{\partial w_{i3}}$， $k_1,k_2,{\epsilon }_1,{\epsilon }_2$ 均为正常数， ${\hat{f}}_{si},{\hat{f}}_{si2}$ 是故障项 $f_{si},f_{si2}$ 的估计值。

而 $v_{i1},v_{i2}$ 设计成如下形式：

$v_{i1}=-k_3{\sigma }_{i3}+{\stackrel{\dot{}}{w}}_{i4d}-f_{i1}-\delta {\hat{f}}_{i1}$ (14)

$v_{i2}=g_2^{-1}\left[-k_4{\sigma }_{i4}-f_{i2}-\delta {\hat{f}}_{i2}-{\displaystyle \underset{j\in {\mathcal{N}}_i}{\sum }{a}_{ij}}\left(w_{i6}-{\hat{f}}_{si3}-w_{j6}\right)-b_i\left(w_{i6}-{\hat{f}}_{si3}-w_{r6}\right)+b_i{\stackrel{\dot{}}{w}}_{r6}\right]$ (15)

其中 $k_3,k_4$ 也为正常数， $\delta {\hat{f}}_{i1},\delta {\hat{f}}_{i2},{\hat{f}}_{si3}$ 分别为 $\delta f_{i1},\delta f_{i2},f_{si3}$ 的估计值。

以上所有估计值分别满足如下更新律：

${\stackrel{\dot{}}{\hat{f}}}_{si1}=-k_1\left[\left({\displaystyle \underset{j\in {\mathcal{N}}_i}{\sum }{a}_{ij}}+b_i\right)e_{i1}-{\displaystyle \underset{k\in ch\left(i\right)}{\sum }{a}_{ki}{e}_{k1}}\right]+{\beta }_1{\tilde{f}}_{si1}$ (16)

${\stackrel{\dot{}}{\hat{f}}}_{si2}=-{\sigma }_{i2}+{\beta }_2{\tilde{f}}_{si2}$ (17)

${\stackrel{\dot{}}{\hat{f}}}_{si3}=-\left({\displaystyle \underset{j\in {\mathcal{N}}_i}{\sum }{a}_{ij}}+b_i\right){\sigma }_{i4}+{\displaystyle \underset{k\in ch\left(i\right)}{\sum }{a}_{ki}{\sigma }_{k4}}+{\beta }_3{\tilde{f}}_{si3}$ (18)

$\delta {\stackrel{\dot{}}{\cancel{\hat{f}}}}_{i1}={\sigma }_{i3}+{\beta }_4\delta {\tilde{f}}_{i1}$ (19)

$\delta {\stackrel{\dot{}}{\cancel{\hat{f}}}}_{i2}={\sigma }_{i4}+{\beta }_5\delta {\tilde{f}}_{i2}$ (20)

其中 $e_{i1}\triangleq u_{i1}{g}_1\left(\tau \left(w_{i3d}\right)-\tau \left({\bar{w}}_{i3}\right)\right)$，估计误差定义为 ${\tilde{f}}_{sij}\triangleq f_{sij}-{\hat{f}}_{sij}$ ( $j=1,2,3$ )， $\delta {\tilde{f}}_{ik}\triangleq \delta f_{ik}-\delta {\hat{f}}_{ik}$ ( $k=1,2$ )， ${\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4,{\beta }_5$ 均为正常数。

接着，针对所有能直接接收故障节点i信息的节点j ( $j\in R_i$ )设计与(7)~(10)相同形式的动态面，因为所有j均无故障，故模型满足(2)~(3)，相应的有：

$\begin{array}{c}{\stackrel{\dot{}}{w}}_{j3d}=\frac{J^{-1}\left(w_{j3d}\right)}{{\epsilon }_1}\{\frac{g_1^{-1}}{u_{j1}}\times [-k_1{\sigma }_{j1}-b_j\left(w_{j2}-w_{r2}\right)-{\displaystyle \underset{k\in {\mathcal{N}}_j}{\sum }{a}_{jk}}\left(w_{j2}-w_{k2}\right)\\ +b_j{\stackrel{\dot{}}{w}}_{r2}-a_{ji}{\hat{f}}_{si1}-{\epsilon }_1\frac{\text{d}{u}_{j1}{g}_1}{\text{d}t}\tau \left(w_{j3d}\right)]-\tau \left(w_{j3d}\right)\}\end{array}$ (21)

${\stackrel{\dot{}}{w}}_{j4d}=\frac{1}{{\epsilon }_2}\left(-k_2{\sigma }_{j3}+{\stackrel{\dot{}}{w}}_{j3d}-w_{j4d}\right)$ (22)

${\stackrel{\dot{}}{v}}_{j1}=-k_3{\sigma }_{j3}+{\stackrel{\dot{}}{w}}_{j4d}-f_{j1}$ (23)

$v_{j2}=g_2^{-1}\left[-k_4{\sigma }_{j4}-f_{j2}-{\displaystyle \underset{k\in {\mathcal{N}}_j}{\sum }{a}_{jk}}\left(w_{j6}-w_{j6}\right)-a_{ji}{\hat{f}}_{si3}-b_j\left(w_{j6}-w_{r6}\right)+b_j{\stackrel{\dot{}}{w}}_{r6}\right]$ (24)

最后，针对所有剩余的无故障节点k ( $k\in {\mathcal{V}}_h$ )，设计如下形式的控制律：

$\begin{array}{c}{\stackrel{\dot{}}{w}}_{k3d}=\frac{J^{-1}\left(w_{k3d}\right)}{{\epsilon }_1}\{\frac{g_1^{-1}}{u_{k1}}\times [-k_1{\sigma }_{k1}-b_k\left(w_{k2}-w_{r2}\right)-{\displaystyle \underset{i\in {\mathcal{N}}_k}{\sum }{a}_{ki}}\left(w_{k2}-w_{i2}\right)\\ +b_k{\stackrel{\dot{}}{w}}_{r2}-{\epsilon }_1\frac{\text{d}{u}_{k1}{g}_1}{\text{d}t}\tau \left(w_{k3d}\right)]-\tau \left(w_{k3d}\right)\}\end{array}$ (25)

${\stackrel{\dot{}}{w}}_{k4d}=\frac{1}{{\epsilon }_2}\left(-k_2{\sigma }_{k3}+{\stackrel{\dot{}}{w}}_{k3d}-w_{k4d}\right)$ (26)

${\stackrel{\dot{}}{v}}_{k1}=-k_3{\sigma }_{k3}+{\stackrel{\dot{}}{w}}_{k4d}-f_{k1}$ (27)

$v_{k2}=g_2^{-1}\left[-k_4{\sigma }_{k4}-f_{k2}-{\displaystyle \underset{i\in {\mathcal{N}}_k}{\sum }{a}_{ki}}\left(w_{k6}-w_{i6}\right)-b_k\left(w_{k6}-w_{r6}\right)+b_k{\stackrel{\dot{}}{w}}_{r6}\right]$ (28)

5. 稳定性分析

至此，我们可以得到定理1：

定理1考虑一个有n架相同四旋翼直升机的编队系统，其拓扑结构满足条件1且系统可分解为 $\mathcal{V}\triangleq \left\{{\mathcal{V}}_f,{\mathcal{V}}_r,{\mathcal{V}}_h\right\}$，其中 ${\mathcal{V}}_r,{\mathcal{V}}_h$ 中所有个体模型满足式(2)~(3)， ${\mathcal{V}}_f$ 中所有个体模型满足式(5)~(6)。 ${\mathcal{V}}_f,{\mathcal{V}}_r,{\mathcal{V}}_h$ 中所有个体分别在控制律(12)~(15)，(21)~(24)，(25)~(28)的作用下，能使整个编队系统保持预设的队形，且

主机能跟踪上外界参考信号，即 ${\psi }_i-{\psi }_j\to 0$， ${\left[x_i-x_j,y_i-y_j,z_i-z_j\right]}^{\text{T}}\to d_{ij}$， ${\left[x_1,y_1,z_1,{\psi }_1\right]}^{\text{T}}\to r$，当 $t\to \infty$，其中 $j\in {\mathcal{N}}_i$。

证明：将编队中所有四旋翼的动态面增广成列栈向量的形式，如下：

${\sigma }_1\triangleq \left[w_2-\left(B\otimes I_2\right)\left(w_{r2}\otimes I\right)\right]+\left[\left(L+B\right)\otimes I_2\right]\left(w_1-w_{r1}\otimes I\right)-\left(\mathcal{A}\otimes I_2\right)\times C$

${\sigma }_2\triangleq w_3-w_{3d},{\sigma }_3\triangleq w_4-w_{4d}$

${\sigma }_4\triangleq \left[w_6-\left(B\otimes I_2\right)\left(w_{r6}\otimes I\right)\right]+\left[\left(L+B\right)\otimes I_2\right]\left(w_5-w_{r5}\otimes I\right)-\left(\mathcal{A}\otimes I_2\right)\times H$

其中 $w_p^{\text{T}}={\left[w_{1p},\cdots ,w_{np}\right]}^{\text{T}}$，( $p=1,\cdots ,6$ )， $C\triangleq {\left[d_{ijxy}\right]}^{\text{T}}$， $H\triangleq {\left[h_{ij}\right]}^{\text{T}}$，( $i=1,\cdots ,n$ )， $I\triangleq {\left[1,\underset{n-1}{\underset{︸}{0,\dots ,0}}\right]}^{\text{T}}$， $B=b_{1}I$。

求 ${\sigma }_1$ 的导数，得到：

${\stackrel{\dot{}}{\sigma }}_1=\left(U_1\otimes I_2\right)G_1\tau \left(w_3\right)-\left(B\otimes I_2\right)\left({\stackrel{\dot{}}{w}}_{r2}\otimes I\right)+\left[\left(L+B\right)\otimes I_2\right]\left(w_2-f_{s1}-w_{r2}\otimes I\right)$ (29)

其中 $U_1\triangleq diag\left(u_{11},\cdots ,u_{n1}\right)$， $\tau \left(w_3\right)$ 是 $\tau \left(w_{i3}\right)$ 增广成的列栈向量， $G_1\triangleq diag\left(g_1\left(w_{15}\right),\cdots ,g_1\left(w_{n5}\right)\right)$， $f_{s1}$ 是 $f_{si1}$ 增广成的列栈向量，即 $f_{s1}\triangleq \underset{n}{\underset{︸}{{\left[0,\cdots ,0,f_{si1},0,\cdots ,0\right]}^{\text{T}}}}$。

故将虚拟输入 ${\bar{w}}_3$ 设计成满足如下条件：

$\tau \left({\bar{w}}_3\right)={\left[\left(U_1\otimes I_2\right)G_1\right]}^{-1}\left\{-k_1{\sigma }_1-\left[\left(L+B\right)\otimes I_2\right]\left(w_2-{\hat{f}}_{s1}-w_{r2}\otimes I\right)+\left(B\otimes I_2\right)\left({\stackrel{\dot{}}{w}}_{r2}\otimes I\right)\right\}$ (30)

其中 ${\hat{f}}_{s1}$ 是 $f_{s1}$ 的估计值。

根据动态面控制方法的设计思路，使 $\left(U_1\otimes I_2\right)G_1\tau \left({\bar{w}}_3\right)$ 通过如下的一阶滤波器：

$\begin{array}{c}\left(U_1\otimes I_2\right)G_1\tau \left({\bar{w}}_3\right)\triangleq {\epsilon }_1\frac{\text{d}\left(U_1\otimes I_2\right)G_1\tau \left(w_{3d}\right)}{\text{d}t}+\left(U_1\otimes I_2\right)G_1\tau \left(w_{3d}\right)\\ =\left(U_1\otimes I_2\right)G_1\left[{\epsilon }_{1}J\left(w_{3d}\right){\stackrel{\dot{}}{w}}_{3d}+\tau \left(w_{3d}\right)\right]+{\epsilon }_1\frac{\text{d}\left(U_1\otimes I_2\right)G}{\text{d}t}\tau \left(w_{3d}\right)\end{array}$ (31)

其中 $J\left(w_{3d}\right)\triangleq diag\left(J\left(w_{13d}\right),\cdots ,J\left(w_{n3d}\right)\right)$， ${\epsilon }_1$ 是滤波器的时间常数，且 $w_{3d}\left(0\right)={\bar{w}}_3\left(0\right)$。

由此我们可以得到：

$\begin{array}{c}{\stackrel{\dot{}}{w}}_{3d}=\frac{J^{-1}\left(w_{3d}\right)}{{\epsilon }_1}{\left[\left(U_1\otimes I_2\right)G_1\right]}^{-1}\{-k_1{\sigma }_1-\left[\left(L+B\right)\otimes I_2\right]\left(w_2-{\hat{f}}_{s1}-w_{r2}\otimes I\right)\begin{array}{c}\\ \end{array}\\ +\left(B\otimes I_2\right)\left({\stackrel{\dot{}}{w}}_{r2}\otimes I\right)-{\epsilon }_1\frac{\text{d}\left(U_1\otimes I_2\right)G}{\text{d}t}\tau \left(w_{3d}\right)-\left(U_1\otimes I_2\right)G_1\tau \left(w_{3d}\right)\}\end{array}$ (32)

同理，求 ${\sigma }_2$ 的导数可以求出另一虚拟输入 ${\bar{w}}_4$，如下：

${\bar{w}}_4=-k_2{\sigma }_2+{\stackrel{\dot{}}{w}}_{3d}+{\hat{f}}_{s2}$ (33)

其中 ${\hat{f}}_{s2}$ 是 $f_{s2}$ 的估计值， $f_{s2}\triangleq {\underset{n}{\underset{︸}{\left[0,\cdots ,0,f_{si2},0,\cdots ,0\right]}}}^{\text{T}}$。

同样使 ${\bar{w}}_4$ 通过与式(31)形式相同的一阶滤波器：

${\bar{w}}_4\triangleq {\epsilon }_2{\stackrel{\dot{}}{w}}_{4d}+w_{4d}$ (34)

可以得到：

${\stackrel{\dot{}}{w}}_{4d}=\frac{1}{{\epsilon }_2}\left(-k_2{\sigma }_2+{\stackrel{\dot{}}{w}}_{3d}+{\hat{f}}_{s2}-w_{4d}\right)$ (35)

接下来，通过求 ${\sigma }_3,{\sigma }_4$ 的导数，得到系统的控制输入 $v_1,v_2$，形式如下：

$v_1=-k_3{\sigma }_3+{\stackrel{\dot{}}{w}}_{4d}-f_1-\delta {\hat{f}}_1$ (36)

$v_2=G_2^{-1}\left\{-k_4{\sigma }_4-f_2-\delta {\hat{f}}_2-\left[\left(L+B\right)\otimes I_2\right]\left(w_6-{\hat{f}}_{s3}-w_{r6}\otimes I\right)+\left(B\otimes I_2\right)\left({\stackrel{\dot{}}{w}}_{r6}\otimes I\right)\right\}$ (37)

其中 $G_2\triangleq diag\left(g_2\left(w_{13}\right),\cdots ,g_2\left(w_{n3}\right)\right)$， $\delta {\hat{f}}_1,\delta {\hat{f}}_2,{\hat{f}}_{s3}$ 分别为 $\delta f_1,\delta f_2,f_{s3}$ 的估计值，且 $\delta f_1,\delta f_2,f_{s3}$ 是为 $\delta f_{i1},\delta f_{i2},f_{si3}$ 的增广，有 $\delta f_1\triangleq {\underset{n}{\underset{︸}{\left[0,\cdots ,0,\delta f_{i1},0,\cdots ,0\right]}}}^{\text{T}}$， $\delta f_2\triangleq {\underset{n}{\underset{︸}{\left[0,\cdots ,0,\delta f_{i2},0,\cdots ,0\right]}}}^{\text{T}}$， $f_{s3}\triangleq {\underset{n}{\underset{︸}{\left[0,\cdots ,0,f_{si3},0,\cdots ,0\right]}}}^{\text{T}}$。

然后，定义如下形式的滤波器误差：

$e_1\triangleq \left(U_1\otimes I_2\right)G_1\left(\tau \left(w_{3d}\right)-\tau \left({\bar{w}}_3\right)\right)$ (38)

$e_2\triangleq w_{4d}-{\bar{w}}_4$ (39)

同样需要定义故障及不确定量的估计误差，如下：

${\tilde{f}}_{si}=f_{si}-{\hat{f}}_{si},i=1,2,3$ (40)

$\delta {\tilde{f}}_i=\delta f_i-\delta {\hat{f}}_i,i=1,2$ (41)

根据式(29)，(30)及(38)，(40)可得到如下形式的 ${\stackrel{\dot{}}{\sigma }}_1$ ：

${\stackrel{\dot{}}{\sigma }}_1=e_1-k_1{\sigma }_1-\left[\left(L+B\right)\otimes I_2\right]{\tilde{f}}_{s1}+\left(U_1\otimes I_2\right)G_1\left[\tau \left(w_3\right)-\tau \left(w_{3d}\right)\right]$

同理，根据式(39)，(40)，可得：

${\stackrel{\dot{}}{\sigma }}_2\text{=}{\sigma }_3+e_2-k_2{\sigma }_2-{\tilde{f}}_{s2}$

考虑式(36)，(37)可得：

${\stackrel{\dot{}}{\sigma }}_3=-k_3{\sigma }_3+\delta {\tilde{f}}_1$

${\stackrel{\dot{}}{\sigma }}_4=-k_4{\sigma }_4+\delta {\tilde{f}}_2-\left[\left(L+B\right)\otimes I_2\right]{\tilde{f}}_{s3}$

此外，根据式(32)与(35)可得：

$\begin{array}{c}{\stackrel{\dot{}}{e}}_1=-\frac{e_1}{{\epsilon }_1}+k_1{e}_1-k_1^2{\sigma }_1+k_1\left(U_1\otimes I_2\right)G_1\left[\tau \left(w_3\right)-\tau \left(w_{3d}\right)\right]\\ +\left[\left(L+B\right)\otimes I_2\right]\left[\left(U_1\otimes I_2\right)G_1\tau \left(w_3\right)-{\stackrel{\dot{}}{\hat{f}}}_{s1}-{\stackrel{\dot{}}{w}}_{r2}\otimes I_2-k_1{\tilde{f}}_{s1}\right]\\ -\left(B\otimes I_2\right)\left({\ddot{w}}_{r2}\otimes I_2\right)\end{array}$

${\stackrel{\dot{}}{e}}_2=-\frac{e_2}{{\epsilon }_2}+k_2\left({\sigma }_3-k_2{\sigma }_2+e_2-{\tilde{f}}_{s2}\right)-{\ddot{w}}_{3d}-{\stackrel{\dot{}}{\hat{f}}}_{s2}$

至此，定义如下形式的Lyapunov函数：

$V=\frac{1}{2}\left({\displaystyle \underset{i=1}{\overset{4}{\sum }}{\sigma }_i^{\text{T}}}{\sigma }_i+{\displaystyle \underset{i=1}{\overset{2}{\sum }}{e}_i^{\text{T}}}{e}_i+{\displaystyle \underset{i=1}{\overset{2}{\sum }}{\left(\delta {\tilde{f}}_i\right)}^{\text{T}}}\delta {\tilde{f}}_i+{\displaystyle \underset{i=1}{\overset{3}{\sum }}{\tilde{f}}_{si}^{\text{T}}}{\tilde{f}}_{si}\right)$

对该Lyapunov函数求导，可得：

$\begin{array}{c}\stackrel{\dot{}}{V}\le -k_4{\Vert {\sigma }_4\Vert }^2+\frac{1}{2}\left(1+{\epsilon }_3\left|1-k_1^2\right|-2k_1\right){\Vert {\sigma }_1\Vert }^2\text{+}\frac{1}{2}\left(1-2k_2+{\epsilon }_4\left|1-k_2^2\right|\right){\Vert {\sigma }_2\Vert }^2\\ +\frac{1}{2}\left(-2k_3+k_2+1\right){\Vert {\sigma }_3\Vert }^2+\left(-\frac{1}{{\epsilon }_1}+k_1+\frac{\left|1-k_1^2\right|}{2{\epsilon }_3}+\frac{k_1+1}{2}\right){\Vert e_1\Vert }^2\\ +\left(-\frac{1}{{\epsilon }_2}+\frac{\left|1-k_2^2\right|}{2{\epsilon }_4}+\frac{3k_2+1}{2}\right){\Vert e_2\Vert }^2+\frac{k_2+1}{2}{a}_1^2+\frac{1}{2}{a}_2^2+\frac{1}{2}{a}_3^2-{\displaystyle \underset{i=1}{\overset{3}{\sum }}{\beta }_i}{\Vert f_{si}\Vert }^2\\ -{\sigma }_1^{\text{T}}\left[\left(L+B\right)\otimes I_2\right]{\tilde{f}}_{s1}-e_1^{\text{T}}\left[\left(L+B\right)\otimes I_2\right]{\stackrel{\dot{}}{\hat{f}}}_{s1}+{\tilde{f}}_{s1}^{\text{T}}{\stackrel{\dot{}}{f}}_{s1}\\ -e_2^{\text{T}}{\stackrel{\dot{}}{\hat{f}}}_{s2}+{\tilde{f}}_{s2}^{\text{T}}{\stackrel{\dot{}}{f}}_{s2}-{\sigma }_4^{\text{T}}\left[\left(L+B\right)\otimes I_2\right]{\tilde{f}}_{s3}+{\tilde{f}}_{s3}^{\text{T}}{\stackrel{\dot{}}{f}}_{s3}\end{array}$

其中 $a_1\ge \Vert \left(U_1\otimes I_2\right)G_1\left[\tau \left(w_3\right)-\tau \left(w_{3d}\right)\right]\Vert$， $a_3\ge \Vert {\stackrel{\dot{}}{w}}_{3d}\Vert$， $a_2\ge \Vert -\left(B\otimes I_2\right)\left({\ddot{w}}_{r2}\otimes I_2\right)+\left[\left(L+B\right)\otimes I_2\right]\left[\left(U_1\otimes I_2\right)G_1\tau \left(w_3\right)-{\stackrel{\dot{}}{w}}_{r2}\otimes I_2\right]\Vert$， $a_4\ge \Vert \left(L+B\right)\otimes I_2\Vert$。

进而，有

$\begin{array}{c}\stackrel{\dot{}}{V}\le \left(-k_4+\frac{a_4}{2}\right){\Vert {\sigma }_4\Vert }^2+\frac{1}{2}\left(1+a_4+{\epsilon }_3\left|1-k_1^2\right|-2k_1\right){\Vert {\sigma }_1\Vert }^2\\ +\frac{1}{2}\left(1-2k_2+{\epsilon }_4\left|1-k_2^2\right|\right){\Vert {\sigma }_2\Vert }^2+\frac{1}{2}\left(-2k_3+k_2+1\right){\Vert {\sigma }_3\Vert }^2\\ +\frac{1}{2}\left(-\frac{2}{{\epsilon }_1}+2k_1+\frac{\left|1-k_1^2\right|}{{\epsilon }_3}+k_1+1+a_4\right){\Vert e_1\Vert }^2\\ +\frac{1}{2}\left(-\frac{2}{{\epsilon }_2}+\frac{\left|1-k_2^2\right|}{{\epsilon }_4}+3k_2+2\right){\Vert e_2\Vert }^2+\left(\frac{a_4+1}{2}-{\beta }_1\right){\Vert {\tilde{f}}_{s1}\Vert }^2\\ +\left(\frac{a_4+1}{2}-{\beta }_3\right){\Vert {\tilde{f}}_{s3}\Vert }^2+\left(\frac{1}{2}-{\beta }_2\right){\Vert {\tilde{f}}_{s2}\Vert }^2+\eta \end{array}$

其中 $\eta =\frac{k_2+1}{2}{a}_1^2+\frac{1}{2}{a}_2^2+\frac{1}{2}{a}_3^2+\frac{a_4}{2}{\Vert {\stackrel{\dot{}}{\hat{f}}}_{s1}\Vert }^2+\frac{1}{2}\left({\Vert {\stackrel{\dot{}}{\hat{f}}}_{s2}\Vert }^2+{\displaystyle \underset{i=1}{\overset{3}{\sum }}{\Vert {\stackrel{\dot{}}{f}}_{si}\Vert }^2}\right)$。

若以下不等式全部成立

$1+a_4+{\epsilon }_3\left|1-k_1^2\right|-2k_1<0,1-2k_2+{\epsilon }_4\left|1-k_2^2\right|<0$

$-2k_3+k_2+1<0,-\frac{2}{{\epsilon }_1}+2k_1+\frac{\left|1-k_1^2\right|}{{\epsilon }_3}+k_1+1+a_4<0$

$-k_4+\frac{a_4}{2}<0,-\frac{2}{{\epsilon }_2}+\frac{\left|1-k_2^2\right|}{{\epsilon }_4}+3k_2+2<0$

$\frac{a_4+1}{2}-{\beta }_1<0,\frac{1}{2}<{\beta }_2$

则根据文献 [16] 可证 $V\to 0$ 当 $t\to \infty$，即可证 $w_{i1}-w_{j1}\to d_{ijxy}$， $z_{ij}\to d_{ijz}$， ${\left[w_{11},w_{15}\right]}^{\text{T}}\to {\left[w_{r1},w_{r5}\right]}^{\text{T}}$， ${\psi }_i\to {\psi }_j$。

6. 仿真实例

本文以加拿大Quanser公司研制的一款名为Qball-X4的四旋翼半物理仿真平台为仿真对象。该平台示意图如图3所示：

Figure 3. Qball-X4

图3. Qball-X4

参考该平台的用户手册 [17]，得到系统参数如下：

$\begin{array}{l}{J}_{\theta }=0.03\text{kg}\cdot {\text{m}}^2,J_{\varphi }=0.03\text{kg}\cdot {\text{m}}^2,\\ J_{\psi }=0.04\text{kg}\cdot {\text{m}}^2,J_r=0.06\text{kg}\cdot {\text{m}}^2,\\ m=1.4\text{kg},l=0.2\text{m}\end{array}$

仿真中，考虑由4架四旋翼直升机(1架主机、3架僚机)组成的主从式编队，其拓扑结构如图4所示。其中节点1是主机，各架直升机之间的连接均为单向的，即信息只从父节点传到子节点，子节点到父节点没有信息的传播。

假设整个编队飞行在同一理想高度，即1 m，而各直升机之间在x-y平面上的理想相对距离设置为：

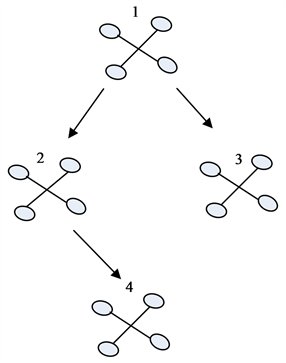
Figure 4. The graph topology of the considered multi-quadrotor systems in simulation

图4. 仿真中四旋翼直升机编队的拓扑结构

$x_1-x_2=1\text{m},y_1-y_2=1\text{m}$，

$x_1-x_3=-1\text{m},y_1-y_3=1\text{m}$，

$x_2-x_4=-1\text{m},y_2-y_4=1\text{m}$。

此外，主机需跟踪的外界参考信号设定为： $r={\left[t\text{m},0.5t\text{m},1\text{m},5^{\circ }\right]}^{\text{T}}$。

各四旋翼直升机的初始位置设定如下：

${\left[x_1\left(0\right),y_1\left(0\right),z_1\left(0\right)\right]}^{\text{T}}={\left[0\text{m},0\text{m},0.8\text{m}\right]}^{\text{T}}$，

${\left[x_2\left(0\right),y_2\left(0\right),z_2\left(0\right)\right]}^{\text{T}}={\left[0\text{m},0.6\text{m},0\text{m}\right]}^{\text{T}}$，

${\left[x_3\left(0\right),y_3\left(0\right),z_3\left(0\right)\right]}^{\text{T}}={\left[0.4\text{m},-0.8\text{m},1.2\text{m}\right]}^{\text{T}}$，

${\left[x_4\left(0\right),y_4\left(0\right),z_4\left(0\right)\right]}^{\text{T}}={\left[-1.1\text{m},-1\text{m},0.9\text{m}\right]}^{\text{T}}$。

初始偏航角设定为： ${\psi }_i\left(0\right)=0^{\circ }$。其他参数设定为： ${\epsilon }_1={\epsilon }_2=0.1$， $k_i=2,\left(i=1,\cdots ,4\right)$， ${\beta }_i=1,\left(i=1,\cdots ,5\right)$。

假设在第8 s后，1号四旋翼直升机的偏航角速度编码器(传感器)发生了偏移故障，偏移量为 $5\sin \left(2t\right){}^{\circ }/\text{s}$。在本文所设计的协同容错控制策略的作用下，仿真结果如图5、图6所示。

仿真结果显示，虽然当发生传感器故障后，1号四旋翼直升机连带其他四旋翼直升机的偏航通道均会出现不同程度的波动，但在所设计的控制策略的作用下，经过较短时间后，它们又重新达到良好的跟踪状态。此外在故障情况下，各四旋翼直升机仍能保持预先设定的队形飞行，且主机始终能在x-y-z空间内跟踪上参考信号。

7. 结论

本文以非线性主从式结构的四旋翼直升机编队系统为研究对象，针对编队中有个体发生传感器故障的情况，设计了一种基于动态面控制的分布式协同容错控制策略，使得整个编队系统在故障情况下仍能保持预设的队形飞行，且主机始终能跟踪上参考信号。本文所提的算法能确保多四旋翼直升机编队系统在飞行中保持队形的能力及良好的跟踪性能。

Figure 5. Position trajectory of each quadrotor in x-y-z space

图5. 各四旋翼直升机在x-y-z空间内的位置轨迹

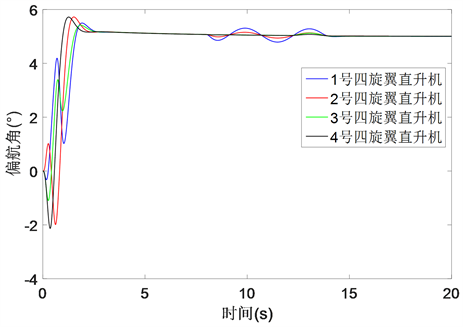
Figure 6. Yaw angle trajectory of each quadrotor

图6. 各四旋翼直升机偏航角轨迹

基金项目

中央高校基本科研业务费(B200201047)。

NOTES

^*通讯作者。