1. 引言
断裂力学经历百年的持续发展已构成完善的理论体系和工程应用方法,并在机械工程、船舶工程、航空航天工程等不同领域的复杂承载结构设计与安全评估中发挥重要作用。断裂力学的理论基础是裂纹尖端奇异应力场及变形场,对于一般各向同性材料建立了工程结构实用断裂准则(应力强度因子K,能量释放率G,J积分,裂纹张开位移COD等) [1] [2] [3]。运用复变函数法求解微积分方程及其线弹性断裂力学边值问题具有特殊效果,克洛索夫–穆斯赫利什维利将复变函数理论用于解决含孔板弹性力学问题取得了卓越成就,尤其是推导出裂纹板的经典解答很完美,利用复变函数求解弹性力学典型问题十分有效,且理论研究热潮方兴未艾 [4] [5] [6]。随着复杂结构材料的不断涌现,断裂力学增添了许多新课题,尤其是先进复合材料的工程应用日益扩张,各向异性材料断裂力学的理论发展显得更加突出。列赫尼茨基推广复变函数法解决各向异性板弹性力学边值问题,并为复合材料断裂力学奠定了理论基础,推动了国际复合材料力学研究和断裂理论新进展 [7] [8] [9]。近年来利用泛复变函数方法解决复合材料应力边值问题方面已取得成效,作者报导了裂纹尖端应力场的研究结果 [10] [11] [12] [13]。由于复合材料力学性能具有各向异性特征,力学理论研究难度大,有待于继续创新和拓展研究思路。本文主要运用泛复变函数及坐标变换方法分析复合材料裂纹板的应力和变形,为进一步发展应用泛复函理论并为有效解决复合材料断裂力学问题提供参考。
2. 弹性力学基本方程及复变函数方法
2.1. 弹性力学基本方程
复合材料的力学性能具有方向性,例如层合板是按工程需要而设计的各向异性材料,其板内的弹性力学分析可按照平面应力状态处理。在薄板面内建立x-y坐标系,则可将各向异性材料在平面应力状态下的本构关系表示为:
(1)
式中常系数
是各向异性材料的柔度系数。一般平面内常用u和v分别表示沿x和y方向的位移,在小变形下应变与位移的关系可用几何方程表示为:
(2)
求解弹性力学平面应力问题的惯用方法就是将应力分量作为基本变量,满足平衡微分方程和应变协调方程,并根据应力边界条件选择合理的应力函数进行求解。为了满足静力平衡微分方程(忽略体力),一般利用应力函数
表示应力如下:
(3)
将式(2)和式(3)代入式(1),就可用应力函数F把变形表达为:
(4)
这是利用一个连续函数表达面内变形,进一步可由式(4)确定出位移函数。显然,由上列方程亦可导得用应力函数表示的变形协调方程,即为:
(5)
式中:
。
上式(5)是一个常系数齐次线性偏微分方程,应力函数F为实函数,可根据给定边值问题选择合适的函数类型,以便求得具体问题的解答。
对于含裂纹复合材料板状结构承受面内加载,可归化为中心裂纹平板在拉伸与剪切混合加载下(如图1所示)的各向异性材料应力边值问题进行求解。各向异性板裂纹问题解决也可借鉴常规材料断裂力学理论与方法。因此需要寻求合理的应力函数满足边界条件和基本方程,下面利用泛复变函数方法也是解决该问题的有效途径。
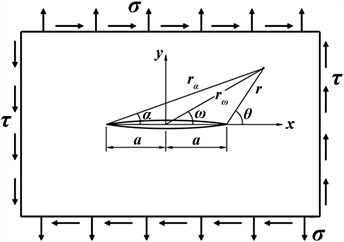
Figure 1. The centre crackplate with mixed-mode loading
图1. 中心裂纹板承受混合型加载
2.2. 复变函数方法
在解决弹性力学某些边值问题时,利用复变函数及其坐标变换法得到了一些经典的结果,若采用实函数求解就十分困难。为了求解复合材料中的弹性力学问题,需要扩展复变函数的理论与方法。先引入泛复变量w及其共轭泛复变量
如下:
(6)
式中复常数为:
(
,且规定
)。具有下列关系:
因此可定义泛复变量的模数或长度为:
(7)
设
是全纯泛复函,
,其共轭复函为:
。关于泛复变函数对坐标变量
的偏导数确定如下:
。
为了解决图1所示的各向异性材料中心裂纹板混合型加载边值问题,可利用泛复函将应力函数
表示为:
(8)
可求得函数对参考坐标轴的偏导数为:
由此可将应力分量表示成复函数形式如下:
(9)
四阶偏微分方程(5)可转化为:
由此确定出参数q所要满足的特征方程:
(10)
根据四次方程的求解方法可确定出四个根(
)。
现在将
记为:
,且选取
,可根据方程(10)的四个根来确定。由此就确定了泛复变量
,即有:
(11)
为求解各向异性材料裂纹体问题,可利用上列两个泛复变量将应力函数表示为:
(12)
可求得偏导数为:
则可把应力分量表示成如下形式:
(13)
再根据式(4),可将各向异性体平面弹性变形用复函数形式表达如下:
(14a)
(14b)
式中常数为:
(14c)
按式(14a)可确定出平面内的位移分量为:
(15)
再根据式(14b)和(14c)可知各个常数必须满足以下关系:
。
3. 含裂纹各向异性板的应力与变形解法
3.1. 全场解答及坐标变换
为便于求解图1所示的中心裂纹板问题,先确定两个复函数如下:
(16)
式中:
对于裂纹长为2a的中心裂纹板(如图1所示),根据断裂力学弹性理论,构造应力函数可选用下列的复变函数:
(17)
则可导得:
则应力表达式(13)可转变为:
(18)
可把位移表达式(15)转变为:
(19)
应力和位移表达式中都包含待定常数,需要根据具体边界条件而确定。
各向异性材料中心裂纹板承受混合型加载(见图1),在距离裂纹面较远区域的应力边界条件是:
则由应力表达式(18)可得:
对于自由裂纹表面
,
,将裂纹处应力边界条件代入式(18)可确定出:
通过以上应力边界条件五个方程组合求解,可得出:
对复数展开化简,经推导后可得:
(20-a)
式中实常数为:
(20-b)
再引入两个实常数
和
在后面使用,具有以下关系式:
(21)
由此可导出下列组合复常数:
式中的实常数确定为:
(22)
由此可导出以下结果:
容易得到虚部和实部如下:
(23)
再列出几个复常数推导结果如下:
(24)
式中实常数表示为:
从图1中的直角坐标与极坐标符号表示可以得出下列关系式:
由此可得:
(25)
上式中采用坐标变换如下:
并规定
都取正值,由此容易确定出下列关系式:
对于泛复变量
可采用如下表达式:
则可将复函数
表达为:
(26)
将以上表达式代入式(18),可使应力分量转化为:
(27)
式中引入了角度参数
,表示如下:
把式(26)代入式(19),可将位移分量转化为:
(28)
将以上各式中的复数展开,经实部与虚部分解,再化简后可得以下结果:
(29-a)
(29-b)
(29-c)
这就是应力分量在整个裂纹板的分布表达式,即为应力全场解。用位移分量表示整个裂纹板的变形状态,位移全场解的表达式为:
(30-a)
(30-b)
3.2. 裂纹端部应力场
前面已经确定出各向异性材料中心裂纹板的应力分量全场解,显然三个应力表达式相当复杂,从式(29)看出裂纹尖端具有应力奇异性。因此在下面就讨论裂纹端部的应力场,以裂纹右端点为应力分析对象,可简化的参数如下:
裂纹右端点附近区域应力分布的表达式可化为:
(31-a)
(31-b)
(31-c)
对于裂纹尖端前沿
的截面(
),应力分量简化为:
(32)
由此可见,应力强度因子
与材料性质无关。
3.3. 裂纹变形分析
各向异性材料中心裂纹板的位移全场解答由式(30)所确定,而裂纹面的相对位移是变形分析的关键。下面利用式(30)给出裂纹面位移表达式。对于裂纹面的边界条件,根据图1可列出以下关系式:
(裂纹上面)
(裂纹下面)
由此通过简化式(30)可将裂纹面位移(上面
,下面
)表示为:
为了表示方便引入记号:
(33)
因此,上下两裂纹面的相对位移为:
(34)
由此可确定出裂纹面的相对位移方程如下:
(35)
显而易见,裂纹面两方向位移状态(滑移型,张开型)呈现为椭圆型方程。在裂纹尖端附近区域(
),
,裂纹面位移表达式(34)简化为:
(36)
即在裂纹尖端处的相对位移方程具有抛物线特征。
4. 计算举例
由于以上公式中出现的参数较多,尤其是基本方程求解需要复数表示,解答也相当复杂。为了更好理解以上公式中各个参数的特点及确定方法,下面举例说明计算过程。现选取各向异性板的柔度系数为:
则可求得:
将以上数据代入式(10)可得:
对四次方程求解,可得四个根为:
由此可得:
利用这些数据计算实常数,计算结果如下:
裂纹端部上下裂纹面相对位移表达为:
裂纹尖端附近区域应力分量表达式转化为:
式中:
以上就是各个参数计算方法,并给出裂纹端部位移和应力场表达式。