1. 引言
聚乙烯(Polyethylene, PE)材料具有耐腐蚀、抗震性好、重量轻、连接方便等优点,作为能源运输管道材料广泛地在国内外被使用,目前在国内城镇燃气管道中的使用比例已达到70% [1]。PE作为一种典型的高聚物材料,具有明显的黏弹性力学行为,其力学响应具有明显的时间相关性。大量实验表明PE材料内部时钟或者特征时间的存在,同时这个特征时间受到诸多因素的影响,例如温度 [2]、应力、和物理老化等等的影响。在对于这些因素的考察过程中,Williams [3] 等提出半经验WLF方程,通过数学方法描述了温度变化与时间之间的等效关系,这种原理即为时间–温度等效原理,并可以通过自由体积理论推导得到 [4]。类比于时间–温度等效原理,Luo [5] 假设应力水平与自由体积分数之间,存在着类似温度与自由体积分数的线性关系,从而推导出一种时间–温度–应力等效原理的表述方式。使用时间、温度、应力三者之间的等效关系,对PE材料长期黏弹性力学行为进行建模和预测已经是较为常用的手段之一 [6] [7]。Lainéa [8] 通过改变温度的方式加速表征PE材料的长期黏弹性力学性能,从而达到预测结构使用寿命的目的。张毅 [9] 基于时间和应变率的新叠加原理,使用一系列松弛测试的结果构建PE长期行为主曲线,这种方法构建的主曲线显示了松弛模量下降具有两个转变。
除应力应变水平、温度对特征时间的影响显著,老化所能造成的影响也经过了大量的研究 [10] [11]。经过老化后PE材料的力学性能发生了一定的变化,其原因在于老化过程中材料结晶度增加,自由体积减少,分子链的活动受到了影响 [12]。老化温度越高,老化时间越长,材料老化程度就越高,造成PE材料的拉伸强度,断裂伸长率减小 [13]。Al-Hadidy [14] 进行了一系列试验确定了老化对于PE和聚丙烯改性沥青混凝土的力学性能的影响。郑健龙参考上述时间与应力、温度之间的等效关系,推导出了一种时间–温度–老化时间等效原理 [15],对沥青材料进行蠕变试验得到了主曲线,并给出了温度变化与老化时间变化之间的关系 [16]。本文考虑老化过程中,老化温度的升高对于材料黏弹性能的影响与延长老化时间的影响类似,对材料特征时间产生类似的改变,推导了一种关于时间–老化温度等效的类似WLF方程的移位因子方程,研究老化后PE材料的室温蠕变行为。
2. 等效理论
2.1. 时间–温度等效原理
根据自由体积理论,材料的黏度
和自由体积分数f的关系是 [4]
(1)
其中,A、B分别是材料常数。同时,有被广泛使用的自由体积分数与温度变化的线性关系:
(2)
式中,
是自由体积分数关于温度的膨胀系数。定义温度移位因子为
,其中
和
分别为参考温度
下的材料黏度和松弛时间,
和
分别为温度T下的材料黏度和松弛时间,就得到了描述时间–温度等效原理的WTL方程 [3]:
(3)
式中,
,
。
类比时间–温度等效的思想,假设自由体积分数与应力水平的线性关系 [17]:
(4)
式中
为自由体积分数的应力膨胀率。假定一个温度–应力联合移位因子
满足
(5)
那么就有关于时间–温度–应力水平三者之间的相互等效的方式 [17]:
(6)
式中,
。
2.2. 时间–温度–老化时间等效原理
考虑到很多高聚物材料,包括PE材料,其特征时间也会受到老化的影响,故而也可以假定老化时间与自由体积分数存在着线性关系。其在忽略应力的影响时可以表达为 [15]:
(7)
式中,h是老化时间,
为参考老化时间,
是自由体积分数关于老化时间的膨胀系数。同样地,定义温度–老化时间联合移位因子满足
,就可以得到时间–温度–老化时间等效关系的一种表现形式 [15]:
(8)
式中,
。
2.3. 时间–老化温度等效原理
经过老化后,PE材料结晶度升高,导致自由体积分数降低 [12]。无论是延长老化时间,或者是提高老化温度,都会造成类似的效果 [18]。所以参考时间–温度–老化时间等效原理的表达方式,我们假定老化温度与自由体积分数之间也存在着一定的线性关系:
(9)
式中,k表示老化温度,
表示自由体积分数关于老化温度的膨胀系数。定义温度–老化温度联合移位因子满足
,则:
(10)
式中,
。
若保持温度恒定,即
,式 将简化为:
(11)
为老化温度移位因子。上式表明了时间与老化温度之间的等效关系,以蠕变柔量D为例,可具体表示为:
(12)
3. 试验设置
试验试样为矩形高密度PE材料(图1),试验设备为Care IPBF-300原位双轴疲劳试验系统,该系统可实现双轴独立控制加载,配有同步非接触式视频引伸计,可完成单轴或双轴拉伸、压缩、蠕变、循环试验。将试样分别放置在环境温度为60℃、80℃、100℃、130℃的老化试验箱内进行老化,保温时间均为36小时,定期取出后在常温(22℃)下存放4小时以上。
取部分试样首先进行常温下单轴简单拉伸试验,加载速率恒为0.1 mm/s。
另取部分试样进行常温下单轴拉伸蠕变试验。加载条件为在拉应力为10.5 MPa保持5000 s,初始加载过程保证匀速增加应力,且不超过11 s。

Figure 1. Schematic diagram of PE material sample
图1. PE材料试样示意图
4. 试验结果与分析
4.1. 简单拉伸试验结果与讨论
单轴简单拉伸试验结果如图2所示,对相同的老化时间(36小时),随着老化温度的升高,PE材料的弹性模量随之增加,屈服极限应力增加,但相应的屈服应变降低。其中在较高温度130℃老化后的试样,很快出现颈缩现象。其原因在于老化过程中,材料结晶度提高,分子链的活动受到影响,故而材料变硬 [12]。
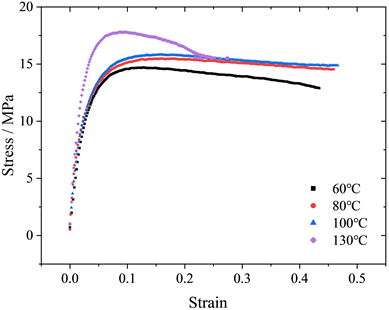
Figure 2. Stress-strain curves of simple tensile tests of sample aged for 36 hours at different temperatures
图2. 不同温度下老化36小时试样的简单拉伸应力–应变曲线
4.2. 拉伸蠕变试验结果与讨论
如图3所示,经过不同温度老化处理后,随着老化温度的升高,PE材料的在蠕变开始时的初始应变逐步降低,蠕变也随之减小,这种变化和一个确定温度下更长时间的蠕变表现相似。符合自由体积理论所阐述的,老化温度越高,自由体积分数越小。这意味着老化时的温度,与应力、试验温度、老化时间都有着类似的对于材料特征时间的影响,可能存在的一种等效关系。其中经过60℃老化和80℃老化后的蠕变曲线相差不大,其主要是因为在36小时老化时间的前提下,在这两个温度下老化的程度较为近似。
对比图4所示各试验的蠕变柔量曲线,尤其是在双对数坐标轴下观察所有蠕变柔量曲线发现,各曲线近乎平行,即老化温度与时间存在一定的等效关系,故视老化温度60℃为参考老化温度,对其余蠕变曲线沿时间对数坐标轴做移位,得到一条如图5所示相较光滑的主曲线,各曲线移位因子见表1。从移位得到的主曲线中,可以看出曲线经过移位后互相重合度较高,且时间轴的尺度变化了大约两个数量级,表明升高老化环境温度的过程中,降低了材料的黏弹力学性能,延长了特征松弛时间。

Figure 3. Creep curves of PE sample aged for 36 hours at different temperatures
图3. 不同温度下老化36小时试样的拉伸蠕变曲线
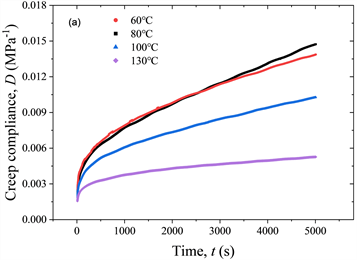
Figure 4. Creep compliance curves of sample aged for 36 hours at different temperatures. (a) Linear coordinates; (b) Double logarithmic coordinates
图4. 不同温度下老化36小时试样的拉伸蠕变柔量。(a) 线性坐标;(b) 双对数坐标
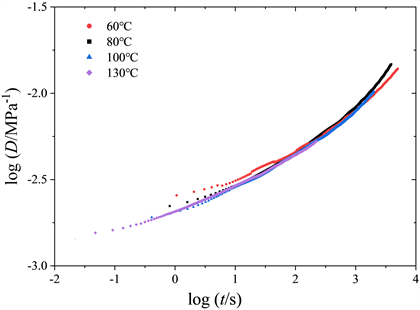
Figure 5. Master creep compliance curve of sample aged for 36 hours at different temperatures
图5. 不同温度下老化36小时试样的蠕变柔量主曲线

Table 1. Shift factors for master creep compliance curve of PE samples aged for 36 hours at different temperatures
表1. 不同温度老化36小时PE试样蠕变柔量主曲线的移位因子
将关于老化温度的移位因子方程(式(11))左右两边做倒数运算,可以得到一个线性关系式:
(13)
将移位结果按照上式进行线性拟合分析,得到如图6所示的结果,数据与模型拟合良好。表示试验中老化温度的改变与材料特征松弛时间之间的关系,符合式(13)所描述的等效关系。
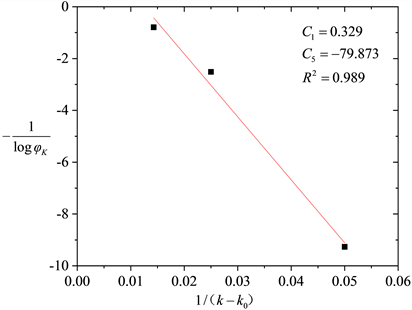
Figure 6. Variation of shift factor with ageing temperature
图6. 移位因子随老化温度的变化
5. 结论
老化使得PE材料弹性模量提高,屈服强度应力变大的同时,对黏弹性能也产生相应的影响,即材料蠕变性能随着老化温度的提高逐渐减小,表现出了类似与温度、应力、老化时间对于特征时间的影响效果。依据自由体积理论,老化温度的提高使得自由体积分数减小,假定其具有一定的线性关系,推导出一种时间–老化温度等效的表达形式。通过不同温度老化处理的试样进行蠕变试验,试验得到的蠕变曲线之间显示出互相近似平行的特点,且可以沿对数坐标轴移位得到相对光滑的主曲线。移位结果表明曲线之间重合度较高,移位因子与老化温度之间的关系符合所推导得到的时间–老化温度等效叠加的移位因子方程,证明了PE材料满足时间–老化温度之间的等效关系。这种等效关系说明当材料老化温度提高,材料特征松弛时间延长,黏弹性能降低。
基金项目
本文由国家市场监督管理总局科技计划项目(2019MK159),湖南省大学生创新创业训练计划项目(S202110530071)资助。