1. 引言
浮筏隔振技术最开始应用于船体舰艇上,我国第一次应用浮筏隔振技术是用于测量船上,进行噪声隔离,并且取得了良好的隔振效果 [1]。随着绿色船舶技术的发展,船用设备的振动噪声控制越来越受到重视,隔振是减小舰船动力设备振动的重要手段。舰船浮筏隔振系统由于特殊要求,朝大型化、轻型化方向发展。将系统各部件视为刚体与实际系统存在很大误差,须将筏体与基础作为柔性体考虑。舰船浮筏隔振系统由于特殊要求,朝大型化、轻型化方向发展。现代舰船多为钢板焊接结构,机械设备质量和功率相对较大,设备振动能量向基础的传递问题比较严重,直接影响机械设备的正常运转和舰船的隐身性能,所以有必要考虑到基础的柔性,由于功率流分析是从振动的能量传递角度来评估隔振效果,比只基于力或振动位移传递率的标准更为直观。因此功率流方法已成为分析柔性基础隔振问题的重要工具 [2]。
振动功率流作为设备振动的评价指标,是描述振动能量在结构中传递的重要物理量,其空间分布可以确定振源、振动的主要传播途径等振动能量信息,对振动分析和噪声控制具有重要的指导意义。采用功率流作为浮筏系统隔振能力的评估指标这一方法,功率流也被验证是比单一速度(加速度、位移)响应更为有效的评价指标 [3]。结构振动中的功率流方法由于其自身的优越性,被越来越广泛地应用于工程实践中如破损诊断及噪声源识别、振动及噪声控制等方面 [4]。
20世纪90年代初,国内开始研究浮筏隔振系统,提出了很多方法并发表了相关论文。江国和等 [5] 以系统固有频率和筏架振动响应为依据,研究隔振器刚度和筏架质量对隔振性能的影响;Sun等 [6] 研究了具有弹性基础的浮筏隔振系统半有源、有源隔振问题;张树桢等 [7] 采用子结构分析法进行柔性浮筏隔振系统的理论建模和隔振性能研究;李增光 [8] 采用阻抗导纳法研究了激励间相位差对输入基座功率流的影响。本文在柔性基础隔振理论研究基础上,建立了柔性浮筏隔振系统模型,利用ABAQUS及其二次开发功能对其进行稳态振动功率流分析,揭示了振动能量在系统中传递的一般特性,并分析了基础刚度、隔振器刚度、机器质量、隔振器安装位置以及隔振器和柔性基础阻尼对隔振效果的影响。
2. 板壳的功率流理论
通过该点的力向量值和速度向量值可以得到某点的功率流。在结构体内部各点的应力和速度都可以通过公式来计算得出。在稳态振动中位移值和速度值都是成正弦变化,并且通过对位移值求导就可以得出速度值,所以,必要时可以使用复位移向量值的导数来代替复速度向量值。在板结构中,可以将流过某一截面的功率流视为一种强度,就像应力一样。这样就能将应力代入到功率流进行求解,得到的即为上章中提到的功率流密度。
由板壳的基本假设,并结合弹性力学中的基本方程,得到用挠度表示的应力方程如下:
(1)
式中:u——沿x方向上的变形;
v——沿y方向上的变形;
w——沿z方向上的变形;
——泊松比;
E——抗拉弹性模量。
为了研究板壳的受力,取微小单元的板壳来研究,微小单元析壳的长宽分别为dx和dy,厚度为t,在微小单元的横截面上三个方向上的作用的应力分别为
、
、
,作用剪力分别为
、
、
,如下图1所示,并且横截面内力作用如图2所示:
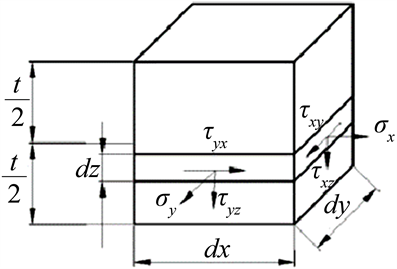
Figure 1. Micro-element stress of plate and shell
图1. 板壳微元应力
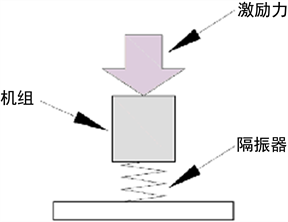 (a) 单层
(a) 单层  (b) 双层
(b) 双层
Figure 2. Schematic diagram of vibration isolation system
图2. 隔振系统示意图
对于弯曲型的板壳问题,截面内力以弯矩、扭矩、侧向力、轴向力和剪力的形式表示,分别为:Mx、My、Mxy、Myx、Qx、Qy、Nx、Ny和Nxy。通过力的平衡方程和积分运算,得到截面各内力表示公式,截面内膜力表达式分别为:
(2)
(3)
(4)
截面弯矩和扭矩表达式分别为:
(5)
(6)
(7)
截面剪力表达式分别为:
(8)
(9)
通过上述公式,我们可以将板壳上的所有内力通过板壳内的应力来求得,这样一来,通过这种简化,将板壳的三维受力化成了板壳中面二维受力,将复杂板壳的三维分析问题简化为了二维分析问题,改变了功率流的计算形式。对于板壳结构,由应力和位移参数表示功率流为:
(10)
(11)
3. 浮筏隔振系统功率流分析
3.1. 浮筏隔振系统介绍
隔振系统有单层隔振系统和双层隔振系统如图2所示。为了改进双层隔振系统中的不足,借鉴了建筑工程领域中的浮动地板的设计,在双层隔振系统的基础上做出了改进,多个主机设备共用一个中间平台,也就是常说的筏架 [9]。浮筏隔振系统不但能够降低动力机械产生的振动和噪声,而且还能使系统更加稳定。在某种程度上来讲,浮筏隔振系统可以看作是复杂了化了的双层隔振系统。
浮筏隔振系统是一个复杂的耦合动力系统,设备和设备之间,设备和筏体之间相互耦合和影响,一部分能量在系统内部发生抵消现象,使整个系统的隔振效果变好。浮筏隔振系统的振动隔离不是将振动源减少,而是改变振动的传播途径来得到减振降噪的目的 [10] [11] [12],这也是浮筏隔振系统的优势所在。筏架的设备可以是弹性连接或者是刚性固定,整个筏架是一个复杂的,多扰动源的混合动力系统。
浮筏隔振系统与一般的隔振系统相比有许多的优点。第一,筏体是非刚性的,因为现在筏体尺寸越来越大,并且其质量原来越小,结构也越来越复杂多样;第二,因为机械设备振动冲击具有多样性,所有需要考虑到各个方向上的隔性能;第三,在实际的工程应用中,基础的机械阻抗是一定的,所有应该看作弹性基础进行计算和设计,这样才能达到设计的隔振效果;第四,筏体具有梁或板乃至结构的特性,连接方式可以设置为弹性或者是刚性。
3.2. 浮筏结构的有限元模型
对浮筏隔振系统建立有限元模型如图3所示,模型做了简化:1) 把振源(一般为电机或机组)简化成一个方形物块,并在物块上施加一个正弦压力作为激励力;2) 因为浮筏隔振系统主要应用在船舶上,所有把把筏架和地板均简化成均质平板结构。在振动过程中,对筏架限制其平动,只允许其上下垂直振动,地板的四边为固支约束。3) 把振动物块和筏架之间及筏架和地板之间的连接隔振器简化成理想的弹簧阻尼系统,其间的连接个数都为四个。
模型尺寸及参数:振动物块,长 × 宽 × 高为1.2 × 0.8 × 0.4 m,弹性模量为210 GPa,泊松比为0.3,密度为7800 kg/m,结构阻尼系数为0.001 Ns/m。筏架是边长为1.6 m的方形板,厚度为0.04 m,弹性模量为210 GPa,泊松比为0.3,密度为7850 kg/m,结构阻尼系数为0.01 Ns/m,其前五阶弹性模态的固有频率为3.35 Hz、20.95 Hz、31.4 Hz、48.41 Hz、63.64 Hz。地板边长3.2 m的方形板,厚度为0.04 m,弹性模量为210 GPa,泊松比为0.3,密度为7800 kg/m,结构阻尼系数为0.01 Ns/m。其上层和下层的隔振器刚度均为1 × 107 N/m,阻尼器系数均为2000 Ns/m。上层隔振器的分布为一个长方形,长方形长a = 1.2 m,宽b = 0.8 m;下层隔振器的分布为一个边长c = 1.6 m的正方形。
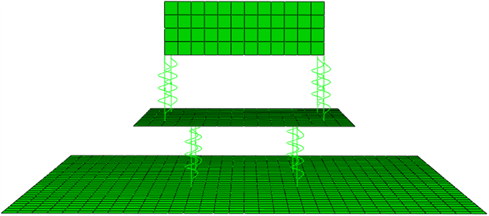
Figure 3. Finite element model of floating raft system
图3. 浮筏隔振系统有限元模型
模型中振动物块采用8节点线性单元C3D8R,筏架和地板均使用4节点线性单元S4R,此单元为4节点四边形有限薄膜应变线性完全积分通用的壳单元。使用直接稳态动力学分析方法来对其振动功率流进行计算,激振力为物块上平面的正弦压力。电动机的的激振力的频率范围取0~150 Hz。建好后的有限元模型如图3所示,其中包括节点1963个,单元1664个。
3.3. 浮筏结构功率流
电机旋转磁场的极对数为1时,此时电机的振动频率为50 Hz,图4给出了50 Hz时地板中的功率流云图和功率流矢量图。

Figure 4. Power flow diagram and power flow vector of floor
图4. 地板功率流云图及矢量图
在地板的功率流云图和矢量图中可以看出,功率流云图和功率流矢量图中存在四个能量比较密集并且矢量为发散形状的点,这四个点是地板与筏架使用隔振器相连接的点,能量从筏架传入到地板上,然后在地板上发散到各个位置处。从图4中还可以看出,能量在地板上的发散过程中,能量会在能量的边缘处发生反射,能量传递到边缘处的过程中会逐渐衰减。
图5是不同频率下物块、地板与筏架包含的功率变化曲线,从图中可以明显看出物块总功率大于筏架总功率,筏架的总功率大于地板总功率。从整体趋势上看频率越大传递到筏架和地板的功率越小,也就是说,激励力的激振频率越大其隔振效果越好。
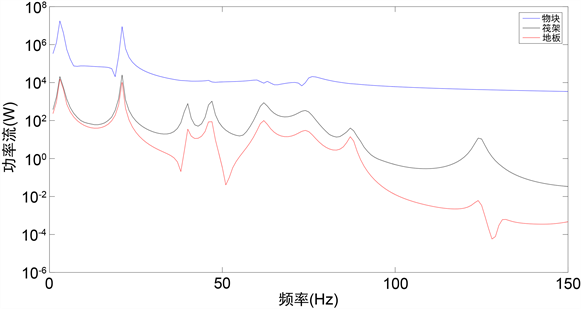
Figure 5. The amount of power contained in each component at different frequencies
图5. 不同频率下各部件所含功率的大小
4. 浮筏隔振系统振动传递特性分析
4.1. 激励力大小对隔振效果的影响
由于在物块上平面施加向下的分布力系,只改变其载荷集度大小为5000 Pa,10,000 Pa,20,000 Pa,传递到基础上的功率流如图6所示。
如图6所示,随着平面的载荷集度减小,功率流的曲线下移,共振峰频率不变。从图6可以看出,改变激励力大小并没有改变共振频率和功率流的变化趋势,仅是功率流的大小发生了变化。
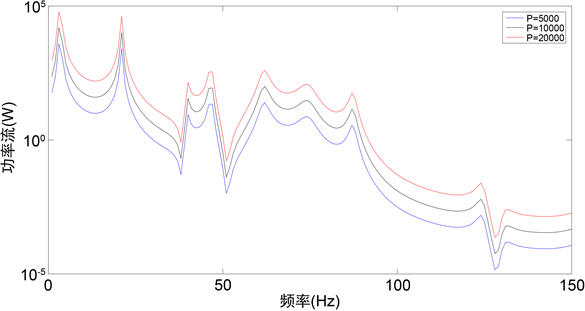
Figure 6. The effect of the incentive force on the power flow
图6. 激励力大小对功率流的影响
4.2. 系统结构参数对隔振效果的影响
研究隔振系统的上层隔振器刚度变化对隔振的影响。令
,
,
,
,改变上层隔振器刚度后传递到基础上的功率流如图7所示。从图中可以看出,随着上层隔振刚度的减小,低频段的共振峰会前移,在高频段对共振频率影响较小。说明在上层隔振器刚度减小到一定程度之后,再减小隔振器刚度,在高频段隔振效果会明显变好,但系统刚度的减小会影响系统的稳定性和抗冲击性能;调整上层隔振器的刚度,使共振峰值前后移动,可以使机器工作频率远离共振频率。
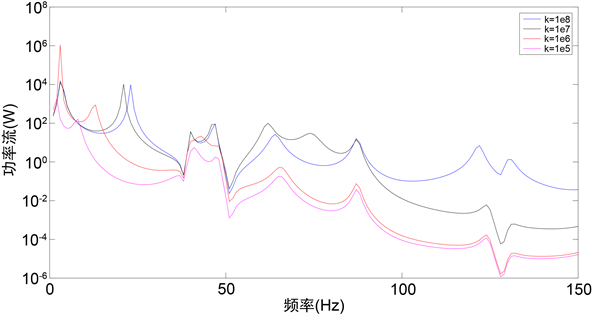
Figure 7. Influence of the upper stiffness on the power flow
图7. 上层隔振器刚度对功率流影响
保持隔振器布置方式不变,改变下层隔振器刚度,令
,
,
,
,
,其传递到基础上的功率流如图8所示,可以看出,随着上层隔振刚度的减小,低频段的共振峰会前移,在高频段对共振频率影响较小。说明在上层隔振器刚度减小到一定程度之后,再减小隔振器刚度,在高频段隔振效果会明显变好,但系统刚度的减小会影响系统的稳定性和抗冲击性能;调整上层隔振器的刚度,使共振峰值前后移动,可以使机器工作频率远离共振频率。
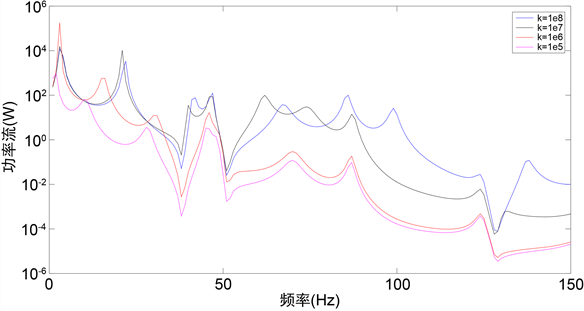
Figure 8. Influence of stiffness of lower isolator on power flow of input base
图8. 下层隔振器刚度对输入基础的功率流影响
保持隔振器布置方式不变,改变上层隔振器阻尼系数,令c = 1000 Ns/m,c = 2000 Ns/m,c = 3000 Ns/m。改变上层隔振器阻尼系数后传递到基础上的功率流如下图9所示。可以看出,增大上层隔振器的阻尼,除了在个别共振点处使得输入到基础的功率流曲线降低外,对功率流曲线影响不明显。这说明:在满足隔振系统稳定性的约束条件及其他限制条件的前提下,增大上层隔振器阻尼系数能减小由系统整体模态共振引起的传递到基础上功率流的峰值,减小共振处的功率流,降低机器通过共振频率时的振动。
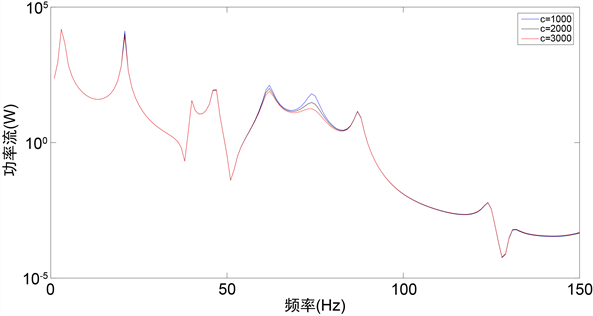
Figure 9. Influence of damping coefficient of upper isolator on power flow of input base
图9. 上层隔振器阻尼系数对输入基础的功率流影响
保持隔振器布置方式不变,改变下层隔振器阻尼系数,令c = 1000 Ns/m,c = 2000 Ns/m,c = 3000 Ns/m,改变下层隔振器阻尼系数后传递到基础上的功率流如图10所示。
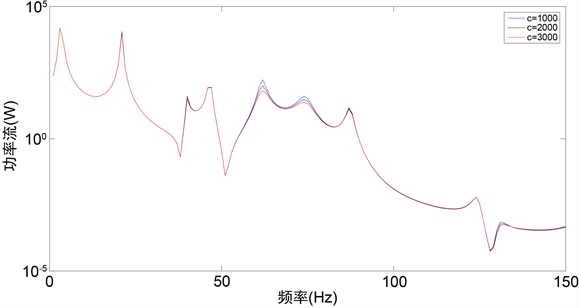
Figure 10. Influence of damping coefficient of lower vibration isolator on power flow of input base
图10. 下层隔振器阻尼系数对输入基础的功率流影响
从图10可以看出,增大下层隔振器的阻尼,除了在个别共振点处使得输入到基础的功率流曲线降低外,对功率流曲线影响不明显。这说明:在满足隔振系统稳定性的约束条件及其他限制条件的前提下,增大下层隔振器阻尼系数能减小由系统整体模态共振引起的传递到基础上功率流的峰值,减小共振处的功率流,降低机器通过共振频率时的振动。
保持系统其他结构参数不变,改变物块质量,令其为2 m,增大物块质量后传递到基础的功率流如图11所示。可以看出,增大物块的质量为2 m后,功率流的曲线整体下移;各共振峰频率除了前两阶略微增大,其余各阶共振频率基本不变。这说明:在满足隔振系统稳定性的约束条件及其他限制条件的前提下,适当增大设备的质量能够减小传递到地板上的功率流。
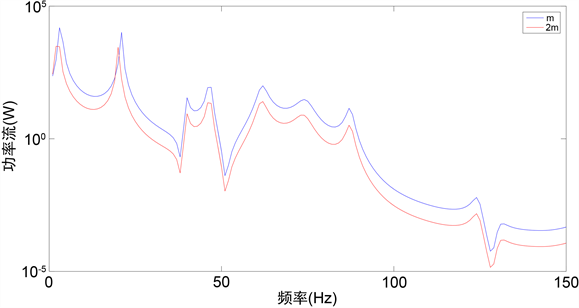
Figure 11. Impact of device quality on the power flow of the input base
图11. 设备质量对输入基础的功率流影响
5. 总结
通过对浮筏隔振系统的软件仿真计算,从振动功率流的方面研究了系统的动态特性,讨论了隔振器刚度、隔振器阻尼、隔振器安装位置以及设备质量等对隔振效果的影响。通过仿真分析,得到以下结论:
1) 在浮筏隔振系统中,物块、筏架、地板的总功率依次减小,也就是通过隔振器后能量越来越少。从整体趋势上看频率越大传递到筏架和地板的功率越小,激励力的激振频率越大其隔振效果越好。
2) 在保证隔振系统稳定性以及其他限制条件的前提下,调整隔振器的安装位置、减小隔振器刚度,增加机器的质量可以减小传递到基础的功率流,从而提高浮筏隔振系统的隔振效果。
3) 增大隔振器的阻尼可以减小共振峰处的功率流大小,使机器通过共振峰的振动不至于太过强烈,但是增大阻尼不能提高浮筏隔振系统的隔振效果。