1. 引言
随着我国基础建设的不断推进,在公路以及铁路修建过程中,隧道工程建设项目越来越多。而在隧道施工建设过程中,由于地形地质条件复杂,导致前期勘察准确度较低,施工过程中的塌方、大变形事故频发。所以采用准确、快速的方法进行超前预报,获得隧道开挖前方的围岩情况,对隧道的安全施工具有重要意义。现阶段,常用的隧道超前预报方法有弹性波法(包括TSP、TRT、TST以及TGP)以及电磁法(GPR和TEM)两大类 [1]。弹性波法探测距离较大(一般大于100 m),且对断层、裂隙等构造反映灵敏,其中TSP法数据处理和解释相对其他方法更加成熟,应用更加广泛。袁永才等利用TSP法准确预报了尚家湾隧道突水突泥等灾害源的规模与空间位置 [2];贾金晓等在千枚岩隧道地区探讨了TSP法超前预报的特征以及解释标志 [3];张杨等对TSP法在隧道超前预报过程中常见的干扰进行研究,并分析总结不同干扰因素在成果中的反映特征 [4];李俊杰等分析了TSP法的探测精度,随后将其用于千岛湖配水工程灰岩地区隧洞超前预报中 [5];吴小川采用TSP法和地质雷达相结合的超前预报技术成功地对万寿山隧道右线出口围岩等级进行划分 [6];蔡盛分别在张吉怀铁路新华山隧道以及张吉怀铁路永顺隧道利用TSP法开展超前预报工作 [7],以上研究工作和成果都为我国隧道施工安全提供了有力的保障。
尽管该方法已经广泛应用到全国范围内的隧道超前预报中,但实际上在隧道地质预报过程中,仍然存在一部分技术人员在为如何提高TSP法的准确性而大费周折,有时会出现数据处理解释准确性较差的问题,这就导致行业内认为TSP法的准确性距离要求还有差距,究其原因是多方面的 [8]。首先,从TSP法的理论入手分析,大部分非专业人员对TSP法原理掌握的不够透彻,所以会盲目地提出一些较为苛刻的要求,比如要求探测岩溶的形状以及探测富水区含水量的大小等。但是由于方法局限性以及解释的多解性,TSP法对于异常体的富水性探测能力较弱,所以需要用正确的理论去指导超前预报工作。本文详细介绍了TSP法的基本原理,对于隧道前方存在低速异常体时,开展了有限差分数值模拟,结合波场快照以及地震记录分析了其地震波场响应特征,为TSP法超前预报实际工作中岩溶等异常体的识别提供了理论依据。在其基础上总结归纳了波速的影响因素,并以山西某隧道超前预报为例进行工程实例研究,以期能够对今后TSP法隧道超前预报工作提供一定的参考价值。
2. TSP法的基本原理
TSP法实质上就是地震反射波法,其与普通的地震方法主要区别在于施工空间 [9]。普通地震方法在地面施工,是均匀的半空间模型,目标体在测线的下方,其主要反射信号来自地下;TSP法在隧道中施工,是不完全的均匀全空间模型,这导致反射信号来自四面八方,TSP法的目标体在测线的正前方,在处理过程中要拾取掌子面前方的有用信号,排除其他方向的干扰信号,增加了处理与解释的难度。在实际TSP法施工过程中,需要在掌子面后方隧道侧帮上布置一系列激发孔(一般是24个),在隧道后方50~55 m范围内侧帮上对称布置接收孔。当在激发孔人工激发地震波后,地震波会在隧道全空间地层中以球面波的形式传播,当传播过程中遇到断层、陷落柱或者岩性分界面时,介质的波阻抗会发生改变,地震波会发生反射 [10]。此时,在接收孔中利用接收器就可以接收到由此产生的地震反射波,如图1所示。
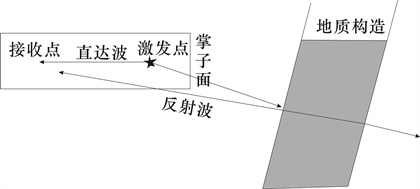
Figure 1. Operating principle of TSP system
图1. TSP系统工作原理
3. Tsp法超前预报数值模拟
3.1. 弹性波有限差分方程
地震波场常用的数值模拟方法有射线追踪法、积分方程法、有限单元法以及有限差分法。其中有限差分法具有计算速度快、精度高、适合复杂模型等优点,被广泛应用于求解波动方程 [11]。因此,本文采用有限差分法开展TSP法超前预报数值模拟,该方法是利用差分近似的代替微分,对波动方程进行离散处理,得到任意时刻不同节点处的波场。对于二维情况,速度–应力弹性波方程为 [12]:
(1)
其中,
和
分别为x方向和z方向上的速度分量,
为岩体的密度,
和
为拉梅系数,t为采集时间,
、
和
分别为应力分量。
采用交错网格有限差分对上式进行离散,计算时分别将速度和应力放在交错网格的节点上,在分析了频散和稳定性条件之后,在边界出采用吸收边界条件,最终得到有限差分迭代公式 [13]。
3.2. 数值模型及模拟结果分析
建立隧道前方存在低速异常体模型,二维模型尺寸为200 m × 200 m,隧道底板位于105 m位置处,高度为10 m,即顶板在95 m位置处;隧道长度为80 m,以模型边界为起点,掌子面位于横向80 m处。垂直低速异常体与掌子面的距离为40 m,该异常在二维剖面的横向位置为120~140 m、纵向位置为60~140 m,即低速异常体的宽为20 m,高80 m,如图2所示。围岩的具体物性参数如下:纵波速度为4000 m/s,横波速度为2000 m/s,密度为1800 kg/m3;隧道的物性参数如下:纵波速度为340 m/s,横波速度为0 m/s,密度为1 kg/m3;垂直低速异常体的物性参数如下:纵波速度为1500 m/s,横波速度为600 m/s,密度为540 kg/m3。观测系统为:震源采用300 Hz雷克子波,采样长度为0.02 s,采样点数为4000,采样间隔为0.05 ms。检波器和震源埋深在底板2 m深度处,偏移距为15 m,道间距1.5 m,检波器个数24个。
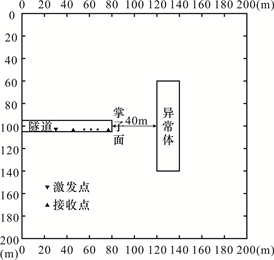
Figure 2. Schematic diagram of advanced forecast model
图2. 超前预报模型示意图
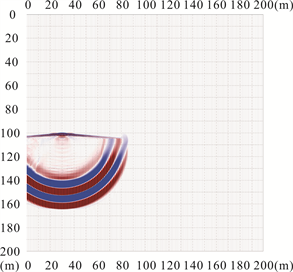
通过数值模拟可以得到不同时刻波场快照(t = 0.01 s、0.026 s、0.05 s和0.08 s),如图3所示。从图中可以看出,当地震波没有传播到异常体时(图3(a)),不会产生反射波,而随着地震波的传播到异常体时(图3(b)),在异常体处会出现反射波、透射波以及绕射波,且随着波的传播,会出现多次反射波(图3(c)、图3(d))。图4所示为地震单炮记录,与波场快照显示一致,从地震记录中可以看到在0.026 s之前没有发现发射波,即地震波没有传播到异常体位置,随着采样时间增加,出现反射波以及多次波。对于隧道前方存在异常时的地震波场传播特征,可以为实际超前预报工作提供理论依据。
 (a)
(a)  (b)
(b) 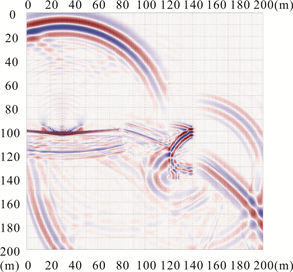 (a)
(a) 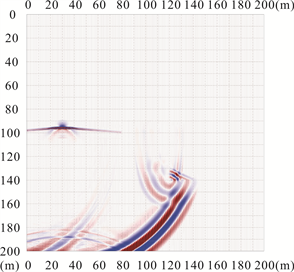 (b)
(b)
Figure 3. Wave field snapshot. (a) Wave field snapshot at 0.01 s; (b) Wave field snapshot at 0.026 s; (c) Wave field snapshot at 0.05 s; (d) Wave field snapshot at 0.08 s
图3. 波场快照。(a) 0.01 s时刻波场快照;(b) 0.026 s时刻波场快照;(c) 0.05 s时刻波场快照;(d) 0.08 s时刻波场快照
4. TSP法超前预报影响参数分析
从上文数值模拟中可以发现,TSP法最直观的参数就是波速,包括纵波速度和横波速度,如果定义纵横波波速比为
,根据TSP法之间参数之间的关系,可以得到 [14]:
(2)
式中,E为杨氏模量,
为岩体的密度,
和
分别是纵波速度和横波速度,
为泊松比,k为弹性模量,
为剪切模量,
为拉梅系数。
从上式中可以发现其它参数包括泊松比、密度、动态杨氏模量等都是通过纵、横波速换算过来的,所以波速准确与否非常重要,如果波速不准确,其他的参数也不准确了,因此解释的基础参数应该还是纵波和横波的波速。而影响波速的因素较多,本文从岩性、孔隙度、岩石的密度、岩石的地质年代、地层的埋深以及初至波波速六个方面对地震波波速的影响进行总结归纳,为后续TSP法的数据解释提供理论依据,具体见表1。

Table 1. Summary of factors affecting seismic wave velocity
表1. 影响地震波波速的因素总结
5. 工程实例
5.1. 工程概况
山西某隧道2斜11+94.0~2斜10+58.0段主要地层为黑云角闪斜长片麻岩,局部花岗岩脉,弱风化,节理裂隙很发育,岩体破碎,呈碎石状压碎结构,设计围岩级别为IV级。在隧道施工过程中,发现掌子面局部呈雨滴状出水,围岩稳定性差,易掉块、坍塌,所以采用TSP法对其进行超前预报工作,查明该段范围内的工程地质及水文地质情况,提供隧道施工建议,保证本段工程合理顺利的施工。
5.2. 观测系统设计
在布设激发孔时,只需要根据隧道内岩层的走向选择掌子面后方的左侧帮或者右侧帮一侧即可,激发孔的布设角度为斜向底板方向10˚~20˚,孔位高度为底板以上1.5 m,布置孔深为1.5 m,激发孔孔距为1.5 m,共24个。在距离掌子面最外侧的一个激发孔后方15~20 m位置处,分别在左、右两侧帮对称布置一个接收孔,孔位高度与激发孔一致,布置孔深为2 m,观测系统布置如图5和图6所示。

Figure 5. Layout of receiving hole and excitation hole
图5. 接收孔和激发孔平面布置图

Figure 6. Section diagram of receiving and excitation holes
图6. 接收孔和激发孔的截面图
5.3. 数据采集
在隧道2斜12+53.76的左、右边墙位置分别布置一个地震波信息接收孔,孔径约为50 mm,孔深均为1.92 m,孔高分别为1.05 m、0.95 m。在2斜12+04.40~2斜12+39.56段的左边墙,按约1.53 m的间距布置24个激发孔分别激发地震波,孔径约40 mm,孔深约为0.75~1.90 m;孔高约为1.05 m,每个激发孔装填的药量约150 g。
5.4. TSP法超前预报成果
图7所示为Z分量地震原始记录,图8所示为TSP超前预报结果,从图中可以看到:1) 2斜11+94~2斜11+52段纵波速度和泊松比呈上升趋势,横波速度和动态杨氏模量呈下降趋势。推测该段围岩岩体破碎,局部较破碎,节理裂隙发育,围岩稳定性差。2) 2斜11+52~2斜11+07段纵波速度和泊松比呈下降–上升–下降趋势,横波速度和动态杨氏模量呈上升–下降–上升趋势。推测该段围岩岩体破碎,节理裂隙发育,围岩稳定性差。3) 2斜11+07~2斜10+58段纵横波速度和泊松比及动态杨氏模量均呈下降趋势。推测该段围岩岩体破碎,节理裂隙发育,局部节理裂隙很发育,围岩稳定性差。
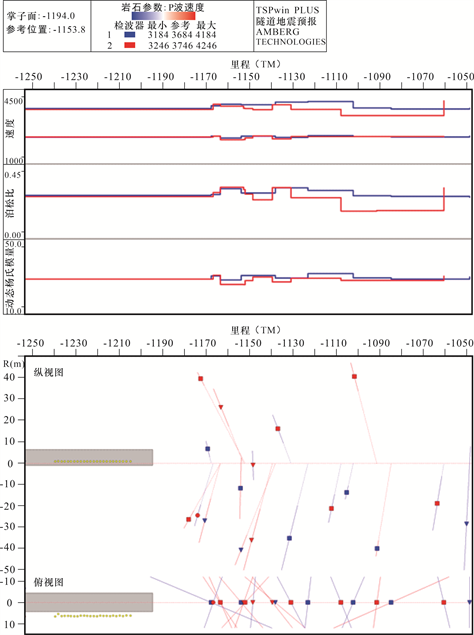
Figure 8. The forecast results of TSP
图8. TSP法超前预报成果图
5.5. 现场开挖验证情况
对于2斜11+94~2斜11+52段,开挖揭示围岩为黑云角闪斜长片麻岩,节理裂隙发育~很发育,岩体破碎;2斜11+52~2斜11+07段,开挖揭示围岩为黑云角闪斜长片麻岩,节理裂隙很发育,岩体破碎;2斜11+07~2斜10+58段,当前开挖段落为黑云角闪斜长片麻岩,节理裂隙很发育,岩体破碎,其中2斜11+02出现塌方。现场验证情况与解释成果基本一致,表明本次超前预报结果准确。
6. 结论
通过介绍TSP法的基本原理和数值模拟,总结了影响波速的因素,结合工程实例可以得到以下结论。
1) 对比不同时刻的波场快照可以看到地震波在空间的传播特征,以及由异常体引起的反射波和绕射波,为TSP法在超前预报实际工作中的异常识别提供了理论依据。
2) 由于其他弹性参数包括泊松比、密度、动态杨氏模量等都是通过纵、横波速换算过来的,所以解释的最基础的参数是纵波和横波的波速。而由于地域及岩性的差异,同样的信号可能导致不同的解释结果。所以需要结合现场实际地质情况进行分析推断,只有不断地将地震波的岩石力学参数与地质知识有机地结合起来,才能更好地提高TSP探测的准确性。
3) 利用TSP法预报了山西某隧道2斜11+94.0~2斜10+58.0段的围岩情况,并通过了现场开挖证明,说明该方法可以准确预报出掌子面前方围岩破碎以及含水异常体,对于类似隧道超前预报工作具有重要的借鉴意义。