一维双曲守恒律方程的基于指数多项式逼近的间断Petrov-Galerkin方法

A Discontinuous Petrov-Galerkin Method Based on Exponential Polynomial Approximation Spaces for One-Dimensional Hyperbolic Conservation Laws

摘要: 本文利用间断Petrov-Galerkin方法求解双曲守恒律方程，使用非代数多项式有限元空间(指数多项式基函数)来构造逼近函数进行空间离散，用SSP Runge-Kutta方法进行时间离散，TVB型minmod限制器用来抑制间断解数值计算时的数值振荡。通过对典型数值算例的计算，并与代数多项式间断Petrov-Galerkin方法的对比，结果显示本文的数值方法有良好的数值计算效果和数值稳定性。

Abstract: In this paper, a discontinuous Petrov-Galerkin method is used to solve the hyperbolic conservation laws. A non-algebraic polynomial finite element space, based on exponential polynomials, is used to construct the approximation function for spatial discretization. The SSP Runge-Kutta method is used for time discretization. The TVB minmod limiter is used to suppress the numerical oscillation in the numerical calculation of discontinuous solutions. Through the calculation of typical numerical examples and the comparison with algebraic polynomial discontinuous Petrov-Galerkin method, the results show that the numerical method in this paper has good numerical effect and numerical stability.

1. 引言

双曲守恒律方程是流体力学中重要的数学模型，在航空航天、气象、海洋等科学工程领域都有广泛的应用，该方程的研究对于揭示自然界及工程技术中存在的基本规律具有重要意义。一般来说，非线性双曲守恒律方程(组)无论初值多么光滑，随着时间推进，方程的解有可能会发生间断。因此，构造合适的数值方法来求解双曲守恒律方程是必要且有意义的。

具有间断解处理能力的数值格式是双曲守恒律数值求解的主流方法。1973年Reed和Hill首次提出间断Galerkin (Discontinuous Galerkin, DG)方法，对中子输送方程进行数值模拟 [1]。此后，Cockburn和Shu将此方法推广应用到求解双曲守恒律方程及方程组，提出了Runge-Kutta间断Galerkin (RKDG)有限元方法 [2] - [7]，此种方法选取的空间允许函数在剖分后的单元边界处出现间断。DG方法具有诸多优点，如数值解具有高精度，多项式次数的选取比较灵活，易于处理复杂区域等。随后，受文献 [8] 的启发，Cockburn和Shu提出了求解对流扩散方程局部间断Galerkin (Local Discontinuous Galerkin, LDG)方法 [9]。LDG方法的基本思路是将一个方程改写为一个一阶的方程组，然后用DG方法求解。此后，LDG方法也被用来求解椭圆方程 [10]、五阶色散方程 [11] 等。陈大伟和蔚喜军在RKDG方法和广义差分的基础上给出一种新的高阶、高分辨率的方法，即控制体积间断有限元方法(RKCVDFEM) [12]。在LDG和RKCVDFEM方法的基础上，文献 [13] [14] [15] 提出了局部间断Petrov-Galerkin (LDPG)方法，LDPG保留了LDG和DPG方法的优点，不仅算式简单，还具有保持物理量局部守恒的特征。Shu提出了基于非代数多项式近似空间的DG方法 [16]，用于数值求解含时双曲型和抛物型以及稳态双曲型和椭圆型偏微分方程。该算法基于由非代数多项式基函数(如指数函数、三角函数等)张成的逼近空间，对特定类型的偏微分方程以及初始和边界条件，相较于基于相同精度阶的多项式近似空间的DG方法，通常可以提供更精确的结果。

本文利用DPG方法对双曲守恒律方程进行数值求解，使用非代数多项式基的有限元空间(指数多项式基)来构造逼近函数进行空间离散。第二部分构造一维双曲守恒律方程间断Petrov-Galerkin方法以进行空间离散；第三部分对几种双曲守恒律方程经典算例，分别使用代数多项式基和指数多项式基进行数值运算，并对运算结果进行比较分析；第四部分为结论。

2. 基于指数多项式逼近的间断Petrov-Galerkin方法

2.1. 空间离散

考虑双曲守恒律方程

$\{\begin{array}{l}{u}_t+f{\left(u\right)}_x=0,a\le x\le b,0\le t\le T\\ u\left(x,0\right)=u_0\left(x\right)\end{array}$ (2.1.1)

其中f是流通量函数。

首先对求解区间进行剖分。将求解区间 $\left[a,b\right]$ 剖分成N个单元格， $a=x_{\frac{1}{2}}\le x_{\frac{3}{2}}\le \cdots \le x_{N+\frac{1}{2}}=b$，记 $x_{j-\frac{1}{2}}\left(j=1,\cdots ,N\right)$ 为剖分节点，第j个单元为 $I_j=\left(x_{j-\frac{1}{2}},x_{j+\frac{1}{2}}\right)$，单元长度 $\Delta x_j=x_{j+\frac{1}{2}}-x_{j-\frac{1}{2}}$， $h={\max }_{1\le j\le N}\Delta x_j$。

选取对偶剖分单元 $I_j^l\left(l=0,\cdots ,k\right)$， $I_j^l=\left(x_j^l,x_j^{l+1}\right)$， $x_j^0=x_{j-\frac{1}{2}}$， $x_j^{k+1}=x_{j+\frac{1}{2}}$，如图1所示

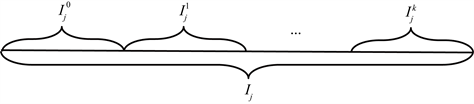
Figure 1. Subdivision of control cell $I_j$

图1. $I_j$ 上的对偶剖分

定义试探函数空间 $U_h=U_h^k=\left\{v:{v|}_{I_j}\in P^k\left(I_j\right),j=1,\cdots ,N\right\}$，其中 $P^k\left(I_j\right)$ 为定义在 $I_j$ 上的k次代数多

项式或其它类型的逼近多项式，每个单元格 $I_j$ 上的基函数为 ${\phi }_j^l\left(x\right)\left(l=0,1,\cdots ,k\right)$。 $I_j$ 上的单元形状函数

$u_h\left(x,t\right)=\underset{l=0}{\overset{k}{{\displaystyle \sum }}}{c}_l\left(t\right){\phi }_j^l\left(x\right),x\in I_j$ (2.1.2)

其中 $c_l\left(t\right)$ 为单元自由度。基于 $I_j$ 上的检验函数空间 $V_h$ 取分片常数空间，相应的基函数为

${\psi }_j^l=\{\begin{array}{l}1,\forall x\in I_j^l\\ 0,\text{otherwise}\end{array}$ (2.1.3)

将原方程两边同时乘以检验函数v，在 $I_j$ 上积分得

${\displaystyle {\int }_{I_j}{u}_{t}v\text{d}x}+{\displaystyle {\int }_{I_j}{u}_{t}v\text{d}x}=0$ (2.1.4)

u用 $u_h$ 代替，检验函数用相应基函数 ${\psi }_j^l$ 代替，并在 $I_j^l$ 上积分得

$\{\begin{array}{l}{\displaystyle {\int }_{I_j^0}{\left(u_h\right)}_{t}v\text{d}x}+{\displaystyle {\int }_{I_j^0}{\left(u_h\right)}_{t}v\text{d}x}=0\\ {\displaystyle {\int }_{I_j^1}{\left(u_h\right)}_{t}v\text{d}x}+{\displaystyle {\int }_{I_j^1}{\left(u_h\right)}_{t}v\text{d}x}=0\\ ⋮\\ {\displaystyle {\int }_{I_j^k}{\left(u_h\right)}_{t}v\text{d}x}+{\displaystyle {\int }_{I_j^k}{\left(u_h\right)}_{t}v\text{d}x}=0\end{array}$ (2.1.5)

分部积分可得

$\{\begin{array}{l}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{I_j^0}{u}_h\text{d}x}=-{f|}_{I_j^0}\\ \frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{I_j^1}{u}_h\text{d}x}=-{f|}_{I_j^1}\\ ⋮\\ \frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{I_j^k}{u}_h\text{d}x}=-{f|}_{I_j^k}\end{array}$ (2.1.6)

将 $u_h$ 表达式代入上式得

$\{\begin{array}{l}\frac{\text{d}{c}_0}{\text{d}t}{\displaystyle {\int }_{I_j^0}{\phi }_j^0\text{d}x}+\frac{\text{d}{c}_1}{\text{d}t}{\displaystyle {\int }_{I_j^0}{\phi }_j^1\text{d}x}+\cdots +\frac{\text{d}{c}_k}{\text{d}t}{\displaystyle {\int }_{I_j^0}{\phi }_j^k\text{d}x}=-{f|}_{I_j^0}\\ \frac{\text{d}{c}_0}{\text{d}t}{\displaystyle {\int }_{I_j^1}{\phi }_j^0\text{d}x}+\frac{\text{d}{c}_1}{\text{d}t}{\displaystyle {\int }_{I_j^1}{\phi }_j^1\text{d}x}+\cdots +\frac{\text{d}{c}_k}{\text{d}t}{\displaystyle {\int }_{I_j^1}{\phi }_j^k\text{d}x}=-{f|}_{I_j^1}\\ ⋮\\ \frac{\text{d}{c}_0}{\text{d}t}{\displaystyle {\int }_{I_j^k}{\phi }_j^0\text{d}x}+\frac{\text{d}{c}_1}{\text{d}t}{\displaystyle {\int }_{I_j^k}{\phi }_j^1\text{d}x}+\cdots +\frac{\text{d}{c}_k}{\text{d}t}{\displaystyle {\int }_{I_j^k}{\phi }_j^k\text{d}x}=-{f|}_{I_j^k}\end{array}$ (2.1.7)

整理得

$\left(\begin{array}{c}\begin{array}{c}\frac{\text{d}{c}_0}{\text{d}t}\\ \frac{\text{d}{c}_1}{\text{d}t}\end{array}\\ \begin{array}{c}⋮\\ \frac{\text{d}{c}_k}{\text{d}t}\end{array}\end{array}\right)=A^{-1}\left(\begin{array}{c}\begin{array}{c}-\left(f\left(u_h\left(x_j^1,t\right)\right)-f_{j-\frac{1}{2}}\right)\\ -\left(f\left(u_h\left(x_j^2,t\right)\right)-f\left(u_h\left(x_j^1,t\right)\right)\right)\end{array}\\ \begin{array}{c}⋮\\ -\left(f_{j+\frac{1}{2}}-f\left(u_h\left(x_j^k,t\right)\right)\right)\end{array}\end{array}\right)$ (2.1.8)

其中

$A=\left(\begin{array}{cc}\begin{array}{cc}{\displaystyle {\int }_{I_j^0}{\phi }_j^0\text{d}x}& {\displaystyle {\int }_{I_j^0}{\phi }_j^1\text{d}x}\\ {\displaystyle {\int }_{I_j^1}{\phi }_j^0\text{d}x}& {\displaystyle {\int }_{I_j^1}{\phi }_j^1\text{d}x}\end{array}& \begin{array}{cc}\cdots & {\displaystyle {\int }_{I_j^0}{\phi }_j^k\text{d}x}\\ \cdots & {\displaystyle {\int }_{I_j^1}{\phi }_j^k\text{d}x}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ {\displaystyle {\int }_{I_j^k}{\phi }_j^0\text{d}x}& {\displaystyle {\int }_{I_j^k}{\phi }_j^1\text{d}x}\end{array}& \begin{array}{cc}\ddots & ⋮\\ \cdots & {\displaystyle {\int }_{I_j^k}{\phi }_j^k\text{d}x}\end{array}\end{array}\right)$ (2.1.9)

在单元交界处允许解间断，由于 $f_{j\pm \frac{1}{2}}$ 无定义，故用相容单调的Lipschitz连续数值流

${\hat{f}}_{j\pm \frac{1}{2}}=\hat{f}\left(u_{j\pm \frac{1}{2}}^{-},u_{j\pm \frac{1}{2}}^{+}\right)$ (2.1.10)

来代替 $f_{j\pm \frac{1}{2}}$，其中

$u_{j-\frac{1}{2}}^{+}=u_h\left(x_{j-\frac{1}{2}},t\right),u_{j+\frac{1}{2}}^{-}=u_h\left(x_{j+\frac{1}{2}},t\right)$ (2.1.11)

本文采用局部Lax-Friedrichs数值流通量，

${\hat{f}}_{j\pm \frac{1}{2}}=\hat{f}\left(u_{j\pm \frac{1}{2}}^{-},u_{j\pm \frac{1}{2}}^{+}\right)=\frac{1}{2}\left[f\left(u_{j\pm \frac{1}{2}}^{+}\right)+f\left(u_{j\pm \frac{1}{2}}^{-}\right)-C\left(u_{j\pm \frac{1}{2}}^{+}-u_{j\pm \frac{1}{2}}^{-}\right)\right]$ (2.1.12)

其中

$C=\underset{\min \left(u_{j\pm \frac{1}{2}}^{-},u_{j\pm \frac{1}{2}}^{+}\right)\le u\le \max \left(u_{j\pm \frac{1}{2}}^{-},u_{j\pm \frac{1}{2}}^{+}\right)}{\max }\left|f^{\prime }\left(u\right)\right|$ (2.1.13)

至此，空间离散完毕，得到常微分方程组

$\frac{\text{d}{U}_h}{\text{d}t}=L_h\left(U_h,t\right)$ (2.1.14)

其中 $U_h$ 为单元自由度构成的向量。

2.1.1. 基于代数多项式的试探函数空间

令 $k=1$，控制单元 $I_j^0=\left(x_{j-\frac{1}{2}},x_j\right)$， $I_j^1=\left(x_j,x_{j+\frac{1}{2}}\right)$， $x_j=\frac{1}{2}\left(x_{j-\frac{1}{2}}+x_{j+\frac{1}{2}}\right)$，常常选取正交代数多项式基函数

${\phi }_j^0\left(x\right)=1,{\phi }_j^1\left(x\right)=\frac{x-x_j}{\Delta x_j}$ (2.1.15)

则

$u_h\left(x,t\right)=c_0\left(t\right){\phi }_j^0\left(x\right)+c_0\left(t\right){\phi }_j^1\left(x\right)$ (2.1.16)

可以算出

$A=\frac{1}{\Delta x_j}\left(\begin{array}{cc}1& 1\\ -4& 4\end{array}\right)$ (2.1.17)

2.1.2. 基于指数多项式的试探函数空间

令 $k=1$，控制单元 $I_j^0=\left(x_{j-\frac{1}{2}},x_j\right)$， $I_j^1=\left(x_j,x_{j+\frac{1}{2}}\right)$，选取指数多项式基

${\phi }_j^0\left(x\right)={\text{e}}^{\left(x-x_j\right)},{\phi }_j^1\left(x\right)=\left(x-x_j\right){\text{e}}^{\left(x-x_j\right)}$ (2.1.18)

则

$u_h\left(x,t\right)=c_0\left(t\right){\phi }_j^0\left(x\right)+c_1\left(t\right){\phi }_j^1$ (2.1.19)

可以算出

$A^{-1}=\frac{1}{\left|A\right|}\left(\begin{array}{cc}\left(\frac{\Delta x_j}{2}-1\right){\text{e}}^{\frac{\Delta x_j}{2}}+1& 1-\left(\frac{\Delta x_j}{2}+1\right){\text{e}}^{-\frac{\Delta x_j}{2}}\\ 1-{\text{e}}^{\frac{\Delta x_j}{2}}& 1-{\text{e}}^{-\frac{\Delta x_j}{2}}\end{array}\right)$ (2.1.20)

其中

$\left|A\right|=\frac{\Delta x_j}{2}\left({\text{e}}^{\frac{\Delta x_j}{2}}+{\text{e}}^{-\frac{\Delta x_j}{2}}\right)-\Delta x_j$ (2.1.21)

2.2. 时间离散

经过空间离散后的常微分方程组(2.1.14)，选用SSP Runge-Kutta方法进行时间离散。令 $t_n\left(n=0,\cdots ,nt\right)$

为 $\left[0,T\right]$ 的剖分，记 $\Delta t=t_{n+1}-t_n$，并且定义 $CFL={\Vert f^{\prime }\Vert }_{L_{\infty }}\frac{\Delta t}{\Delta x}$

$\{\begin{array}{l}{u}^{\left(1\right)}=u^n+\Delta xL\left(u^n,t_n\right)\\ u^{\left(2\right)}=\frac{3}{4}{u}^n+\frac{1}{4}\left(u^{\left(1\right)}+\Delta tL\left(u^{\left(1\right)},t_n+\Delta t\right)\right)\\ u^{n+1}=\frac{1}{3}+\frac{2}{3}\left(u^{\left(2\right)}+\Delta tL\left(u^{\left(2\right)},t_n+\Delta t\right)\right)\end{array}$ (2.2.1)

2.3. 限制器

为提高方法的稳定性，抑制间断附近产生的非物理振荡，在时间方向的步进过程中需引入斜率限制器。本文选用TVB型minmod限制器。单元 $I_j$ 上的积分平均值定义为

${\bar{u}}_j=\frac{1}{\Delta x_j}{\displaystyle {\int }_{I_j}{u}_h\text{d}x}$ (2.3.1)

记

${\tilde{u}}_j=u_{j+\frac{1}{2}}^{-}-{\bar{u}}_j,{\widetilde{\stackrel{˜}{u}}}_j={\bar{u}}_j-u_{j-\frac{1}{2}}^{+}$ (2.3.2)

限制器作用后的 ${\tilde{u}}_i,{\widetilde{\stackrel{˜}{u}}}_i$ 为

${\tilde{u}}_j^{\left(mod\right)}=\tilde{m}\left({\tilde{u}}_j,{\Delta }_{+}{\bar{u}}_j,{\Delta }_{-}{\bar{u}}_j\right),{\widetilde{\stackrel{˜}{u}}}_j^{\left(mod\right)}=\tilde{m}\left({\widetilde{\stackrel{˜}{u}}}_j,{\Delta }_{+}{\bar{u}}_j,{\Delta }_{-}{\bar{u}}_j\right)$ (2.3.3)

其中函数 $\tilde{m}$ 为满足TVB性质的minmod限制器

$\tilde{m}\left(a_1,a_2,a_3\right)=\{\begin{array}{l}{a}_1,\left|a_1\right|\le M{h}^2\\ m\left(a_1,a_2,a_3\right),\text{otherwise}\end{array}$ (2.3.4)

其中 $M>0$ 为常数，M的选取依赖于问题，方式详见文献 [17]。

另外， $m\left(a_1,a_2,a_3\right)$ 为minmod函数

$m\left(a_1,a_2,a_3\right)=\{\begin{array}{l}s\min \left(\left|a_1\right|,\left|a_2\right|,\left|a_3\right|\right),s=\text{sign}\left(a_1\right)=\text{sign}\left(a_2\right)=\text{sign}\left(a_3\right)\\ 0,\text{otherwise}\end{array}$ (2.3.5)

则有

$u_{j+\frac{1}{2}}^{-\left(mod\right)}={\bar{u}}_j+{\tilde{u}}_j^{\left(mod\right)},u_{j-\frac{1}{2}}^{+\left(mod\right)}={\bar{u}}_j-{\widetilde{\stackrel{˜}{u}}}_j^{\left(mod\right)}$ (2.3.6)

则数值流通量 ${\hat{f}}_{j\pm \frac{1}{2}}=\hat{f}\left(u_{j\pm \frac{1}{2}}^{-\left(mod\right)},u_{j\pm \frac{1}{2}}^{+\left(mod\right)}\right)$。

3. 数值算例

3.1. 线性对流方程

令(2.1.1)中 $f\left(u\right)=u$，即线性对流方程

$\{\begin{array}{l}{u}_t+u_x=0\\ u\left(x,0\right)=u_0\left(x\right)\end{array}$ (3.1.1)

令 $CFL=0.1$。

算例1

$u_0\left(x\right)=\sin \left(2\pi x\right)$ (3.1.2)

求解区域为 $\left[-1,1\right]$， $T=0.1$， $N=80$。

表1和表2的计算结果证明了基于指数多项式的间断Petrov-Galerkin方法是具有二阶精度的，而且限制器的使用未出现光滑极值点处降阶现象。

Table 1. Algebraic polynomial approximation spaces

表1. 代数多项式基

Table 2. Exponential polynomial approximation spaces

表2. 指数多项式基

算例2

$u_0\left(x\right)=\{\begin{array}{l}1,x\in \left[-0.2,0.2\right]\\ 0,\text{otherwise}\end{array}$ (3.1.3)

求解区域为 $\left[-1,1\right]$， $T=0.1$， $N=80$。

算例3

$u_0\left(x\right)=\{\begin{array}{l}\sin \left(2\pi x\right),x\in \left[0.3,0.8\right]\\ \cos \left(2\pi x\right)-0.5,\text{otherwise}\end{array}$ (3.1.4)

求解区域为 $\left[0,1\right]$， $T=0.1$， $N=80$。

算例4

$u_o\left(x\right)=\{\begin{array}{l}\frac{1}{6}\left(G\left(x,\beta ,z-\beta \right)+G\left(x,\beta ,z+\beta \right)+4G\left(x,\beta ,z\right)\right),x\in \left[-0.8,-0.6\right]\\ 1,x\in \left[-0.4,-0.2\right]\\ 1-\left|10\left(x-0.1\right)\right|,x\in \left[0,0.2\right]\\ \frac{1}{6}\left(F\left(x,\alpha ,a-\delta \right)+F\left(x,\alpha ,a+\delta \right)+4F\left(x,\alpha ,a\right)\right),x\in \left[0.4,0.6\right]\\ 0,\text{otherwise}\end{array}$ (3.1.5)

求解区域为 $\left[-1,1\right]$， $T=0.1$， $N=80$。

边界条件为周期边界条件，T时刻的精确解为初值沿x轴方向左移T个单位，图2~4给出了不同初值下T时刻时数值解和精确解的对比图，可以看出该格式可以很好地计算间断初值问题，数值解与精确解吻合情况较好且间断附近没有出现任何非物理振荡。

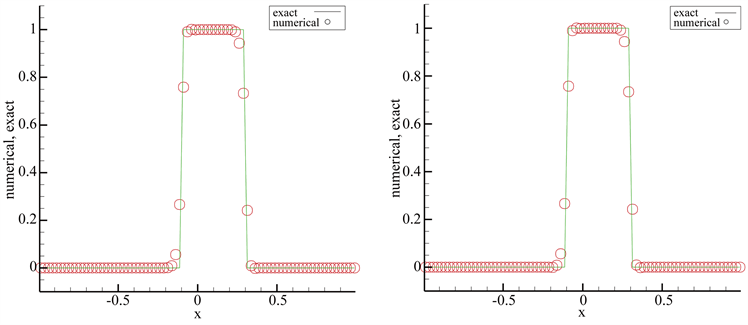
Figure 2. Algebraic polynomial and exponential polynomial approximation spaces

图2. 代数多项式基(左)、指数多项式基(右)

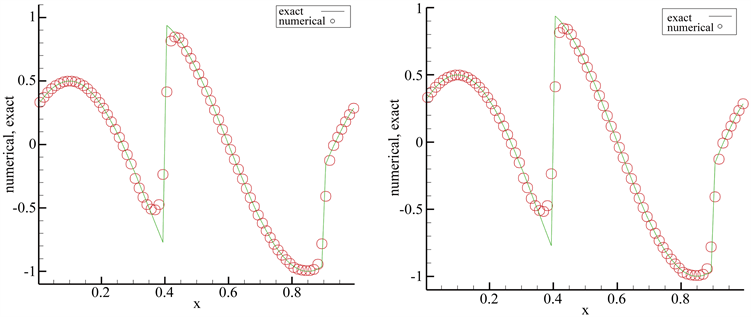
Figure 3. Algebraic polynomial and exponential polynomial approximation spaces

图3. 代数多项式基(左)、指数多项式基(右)

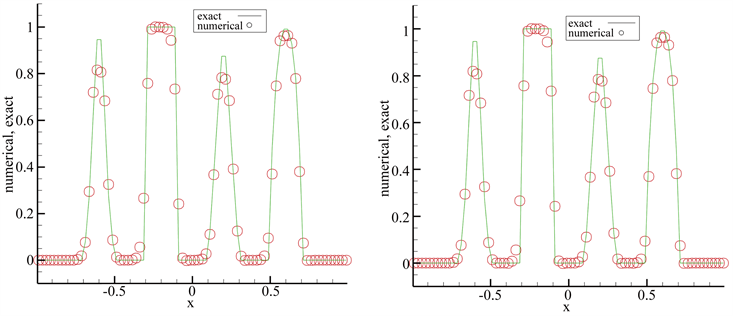
Figure 4. Algebraic polynomial and exponential polynomial approximation spaces

图4. 代数多项式基(左)、指数多项式基(右)

3.2. 无粘Burgers方程

令(2.1.1)中 $f\left(u\right)=\frac{u^2}{2}$，即无粘Burgers方程

$\{\begin{array}{l}{u}_t+{\left(\frac{u^2}{2}\right)}_x=0\\ u\left(x,0\right)=\frac{1}{4}+\frac{1}{2}\sin \left(\pi x\right)\end{array}$ (3.2.1)

令 $CFL=0.1$，求解区域为 $\left[-1,1\right]$， $N=80$。

图5、图6表明，格式对间断有很好的分辨率，在间断附近没有出现任何非物理振荡。

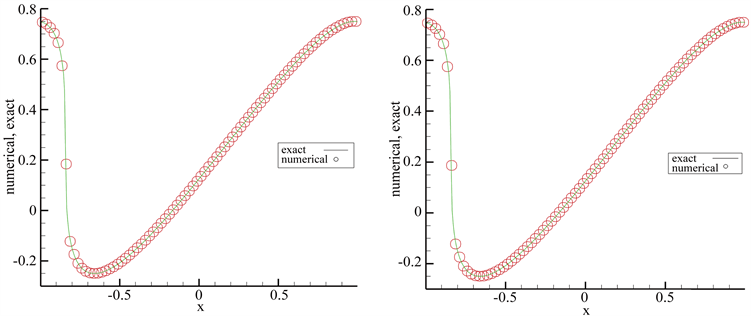
Figure 5. $T=\frac{2}{\pi }$, algebraic polynomial and exponential polynomial approximation spaces

图5. $T=\frac{2}{\pi }$，代数多项式基(左)、指数多项式基(右)

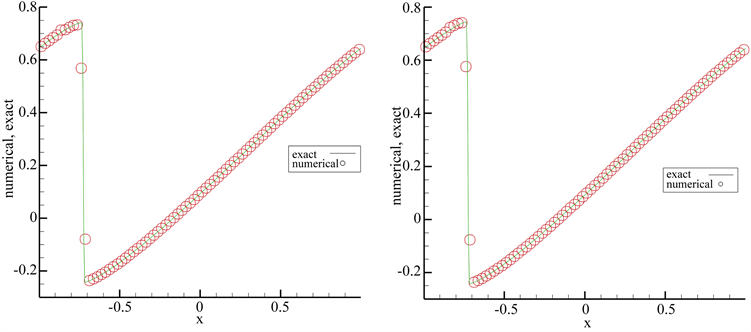
Figure 6. $T=1.1$, algebraic polynomial and exponential polynomial approximation spaces

图6. $T=1.1$，代数多项式基(左)、指数多项式基(右)

3.3. Buckley-Leverett方程

令(2.1.1)中 $f\left(u\right)=\frac{4u^2}{4u^2+{\left(1-u\right)}^2}$，即非凸流通量函数Buckley-Leverett方程

$\{\begin{array}{l}{u}_t+{\left(\frac{4u^2}{4u^2+{\left(1-u\right)}^2}\right)}_x=0\\ u\left(x,0\right)=\{\begin{array}{l}1,x\in \left[-0.5,0\right]\\ 0,\text{otherwise}\end{array}\end{array}$ (3.3.1)

令 $CFL=0.5$，求解区域为 $\left[-1,1\right]$， $T=0.4$， $N=160$。

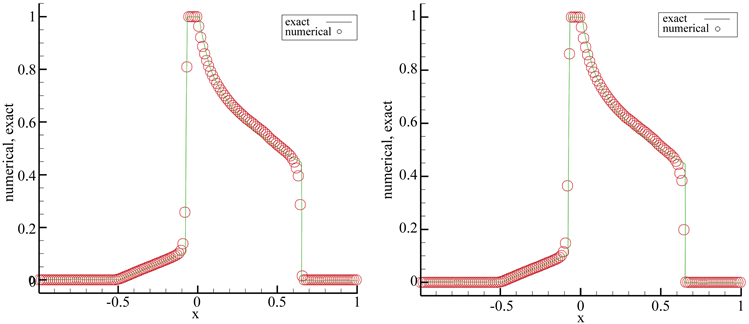
Figure 7. Algebraic and exponential polynomial approximation spaces

图7. 代数多项式基(左)、指数多项基(右)

由图7可知，通过比较数值解与五阶WENO格式下的参考解 [18] [19] 可以发现，该格式计算出的数值解在大梯度处无振荡，可以很好地捕捉间断，而且与参考解在极值处的逼近情况比较好，可以较好地模拟解的形态。

4. 结论

针对双曲守恒律方程，本文结合非代数多项式基(指数多项式基)和间断Petrov-Galerkin方法进行求解，不仅计算公式简单，而且通过对典型数值算例的计算，并与基于代数多项式的间断Petrov-Galerkin方法进行对比，结果显示，基于指数多项式逼近的间断Petrov-Galerkin方法精度阶理想且可以很好地捕捉间断，具有良好的数值计算效果和数值稳定性。

基金项目

内蒙古大学科研发展基金(21100-5187133)；内蒙古自治区人才开发基金项目(12000-1300020240)。