贵州局地T_m模型的建立及时空变化特征分析

Establishment of the Local T_m Model in Guizhou and Its Spatio-Temporal Variation

摘要: 加权平均温度(T_m)作为GNSS反演大气可降水量(PWV)的关键参量，具有较强的区域差异性和时域周期性。针对贵州地形起伏大和气候多变的特点，为提升贵州地区GNSS PWV的探测精度，本文基于欧洲中期天气预报中心发布的ERA5气象数据集，在揭示贵州局域Tm时域周期性的基础上，构建了一种适宜于贵州的高时空分辨率局域Tm格网模型(GZTm)，并基于无线电探空站气象资料计算的Tm，对GZTm的精度进行了评价。结果表明：相比于Bevis模型和GPT2w模型，GZTm在贵阳站的精度分别提高了24.8%和1.0%，在威宁站则分别提高了10.4%和8.1%。此外，基于选定的15个ERA5格网点，本文还对贵州Tm的时空变化特征进行了初步分析，结果显示贵州Tm的季节差异明显，且与站点高程间密切相关，呈现出较强的区域差异性。

Abstract: As a key parameter for GNSS inversion of precipitable water vapour (PWV), the weighted mean temperature (T_m) has strong regional differences and time-domain periodicity. In view of the characteristics of large topographic fluctuation and changeable climate in Guizhou, and in order to improve the precision of GNSS PWV within the Guizhou province, based on the ERA5 meteorological data set released by the European Centre for Medium-Range Weather Forecasts, a high spatio-temporal resolution Tm grid model (GZTm) suitable for Guizhou province was established on the basis of the revealing of the time domain periodicity for Guizhou Tm. Also, the precision of GZTm was evaluated by the Tm computed by the radiosonde dataset. Compared with the Bevis model and the GPT2w model, the results show that the precision of GZTm at Guiyang Station was increased by 24.8% and 1%, and 10.4% and 8.1% for Weining station, respectively. In addition, based on the selected 15 ERA5 grid points, this paper also conducts a preliminary analysis of the temporal and spatial characteristics of Guizhou Tm. The results show that Guizhou Tm owns obvious seasonal differences and is closely related to site elevation, showing strong regional differences.

1. 前言

基于地基GNSS技术的可降水量(precipitable water vapor, PWV)探测，由于具备连续性、全天候、低成本及高精度等优势，已发展成为传统PWV观测手段的强有力补充 [1]。加权平均温度(T_m)作为GNSS技术探测PWV的关键参量，其精度将直接影响PWV反演的准确性 [2]。然而，加权平均温度与季节、测站位置(主要是纬度)及高程密切相关 [3] [4]，导致基于局域气象资料建立的T_m模型用于其它区域时势必引入较大的误差。为此，学者们分别基于本地化气象资料建立了大量的局域T_m模型 [5] [6] [7] [8] [9]。

贵州地貌属于中国西南部高原山地，受大气环流及地形等的影响，省内气候多样性明显，素有“一山分四季，十里不同天”之说。高时空分辨率贵州局地T_m模型的建立，对于采用地基GNSS技术精确获取贵州山地气候条件下的PWV具有重要意义。为此，本文基于欧洲中期天气预报中心(European Centre for Medium-range Weather Forecasts, ECMWF)提供的高时空分辨率ERA5数据集，构建了贵州局地格网T_m模型，并对模型的精度及时空变化特征进行了评价与分析。

2. 数据源及研究区

2.1. ERA5大气再分析产品

ERA5是ECMWF提供的第五代大气再分析产品，具有高空间分辨率(31 km × 31 km，亦即0.25˚ × 0.25˚)和高时间分辨率(1 h) [10]。为采用数值积分法 [11] 计算贵州省境内各格网点的T_m，本文使用了2011~2018年共8年的ERA5 37个压力层的逐小时温度、相对湿度、大气压及位势数据 (https://cds.climate.copernicus.eu/cdsapp#!/search?type=dataset)。其中，相对湿度和大气压用于计算水汽压；位势用于计算测站点的位势高。

2.2. 无线电探空站数据

贵州省内仅有两个无线电探空站(radiosonde station, RS)，分别为贵阳(Guiyang) (26.48˚N, 106.65˚E)和威宁(Weining) (26.86˚N, 104.26˚E)。试验所用RS数据源于怀俄明大学 (https://weather.uwyo.edu/upperair/seasia.html)发布的2019年整年Guiyang和Weining的气象资料，用以计算各自的加权平均温度，并据此评价基于ERA5气象资料所建T_m模型的精度。

2.3. 研究区

以ECMWF ERA5大气再分析产品所覆盖的整个贵州省作为研究区域，区域范围为北纬24˚37'~29˚13'，东经103˚36'~109˚35'，其中选取了15个ERA5格网点和2个RS站(同时也为ERA5格网点)。格网点和RS站的空间分布如图1所示。

Figure 1. The distribution of grid points and radiosonde stations selected in the study area

图1. 研究区内选取的格网点及无线电探空站分布

3. 加权平均温度模型的建立

ERA5和RS的气象数据分别按位势和位势高对不同等压面进行记录，为实现二者积分高度的统一，首先需将ERA5的位势转换为位势高，然后基于ERA5气象数据采用数值积分法计算各格网点的逐小时T_m。大量研究表明，T_m具有时域周期特性 [12] [13] [14]。为确定T_m各时间尺度上的周期，将RS Guiyang站处ERA5格网点2011~2018年的逐小时T_m分别按月和各年对应时刻取平均，得图2所示的T_m时间序列。

Figure 2. T_m time series of ERA5 grid points from 2011 to 2018

图2. 2011~2018年ERA5格网点T_m时间序列

由图2可看出，T_m时间序列均具有明显的周期特性。为确定贵州本地化T_m的频率特征，本文采用Lomb-Scargle对T_m时间序列进行周期诊断，得图3(a)、图3(b)所示T_m的日周期和年周期特性。

Figure 3. Periodic characteristics of grid point T_m

图3. 格网点T_m的周期特性

由图3可知，PSD (Power Spectral Density)表现出12 h、24 h、0.5 a和1 a的周期特性，且日周期比半日周期、年周期比半年周期更为明显；此外，图3(b)中的PSD明显大于图3(a)中的PSD，说明T_m的年际变化较日间变化更为显著。因此，顾及T_m的周期特性，采用(1)式刻画贵州本地化T_m的变化趋势。

$\begin{array}{c}{T}_m=A_0+A_1\cos \left(\frac{doy}{365.25}2\text{π}\right)+A_2\sin \left(\frac{doy}{365.25}2\text{π}\right)+B_1\cos \left(\frac{doy}{365.25}4\text{π}\right)+B_2\cos \left(\frac{doy}{365.25}4\text{π}\right)\\ +C_1\cos \left(\frac{hod}{24}2\text{π}\right)+C_2\sin \left(\frac{hod}{24}2\text{π}\right)+D_1\cos \left(\frac{hod}{24}4\text{π}\right)+D_1\sin \left(\frac{hod}{24}4\text{π}\right)\end{array}$ (1)

(1)式中，hod (hour of day)表示一天中的时间(小时)；doy (day of year)表示年积日；A₀、A₁、A₂、B₁、B₂、C₁、C₂、D₁及D₂为模型待求系数。

以hod、doy和基于2011~2018 ERA5气象资料求得的逐小时T_m为已知值，以3倍中误差为极限误差，在剔除T_m异常值的情况下，采用最小二乘平差即可求得(1)式中的模型系数，从而构建起贵州本地化的高时空分辨率格网加权平均温度模型(以下简称为GZTm)。

4. GZTm模型精度评价

RS提供的大气剖面资料均为实测值，具有较高的精度和可靠性。由于探空站中的Guiyang站和Weining站同时为ERA5格网点，本文视贵州省境内两个仅有的RS站2019年全年气象资料所求得的T_m为参考值，以平均偏差(Bias)和均方根误差(RMSE)作为精度指标，对GZTm模型的精度进行评价。

$\begin{array}{c}\text{Bias}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(X_i-X_{ref}\right)}\\ \text{RMSE}=\sqrt{\frac{1}{n}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(X_i-X_{ref}\right)}}^2}\end{array}\}$ (2)

(2)式中，n为T_m个数，由于RS每天观测2次，故此处 $n=730$ ； $X_i$ 为模型计算所得T_m值； $X_{ref}$ 为T_m参考值。

以hod及doy；测站温度(由探空站气象元素得到)；测站位置及时间分别作为GZTm模型、Bevis公式 [11] 和GPT2w模型 [13] 的输入参量，得表1所示的精度统计信息。

由表1知，GZTm模型在各个精度指标上较其它两个模型皆有一定程度的改善。相较于Bevis公式，Guiyang站和Weining站GZTm模型的Bias分别减少了1.489 K和0.176 K；而对于GPT2w模型，则分别减少了0.107 K和1.468 K。此外，无论是Guiyang站还是Weining站，GZTm模型均获得了更小的RMSE，说明GZTm模型具有更高的可靠性和稳定性。相较于Guiyang站(海拔为1222 m)，基于GPT2w所得Weining (海拔为2236 m)站的T_m具有较大的Bias和RMSE，这可能与Weining站海拔相对较高，而GPT2w却忽略了T_m的垂向改正有关。

Table 1. Accuracy evaluation of GZTm model

表1. GZTm模型精度评价

由Bias绝对值的区间统计图(图4)可知，无论是Guiyang站还是Weining站，GZTm模型和GPT2w模型的Bias绝对值位于0~4 K间的个数相当，Bevis公式则相对较少；位于4~8 K间的个数由多到少分别为Bevis公式、GZTm模型和GPT2w模型；Bias绝对值大于12 K的个数以GZTm模型为最少；随着海拔的增加，GPT2w模型Bias绝对值大于12 K的个数较Bevis公式有所增加。

因此，综合Bias、RMSE及Bias绝对值区间统计可知，三个模型的整体性能按高到低顺序排列分别为GZTm、GPT2w及Bevis公式。

Figure 4. Average deviation statistics

图4. 平均偏差统计

5. 贵州T_m时空变化特征分析

为分析贵州T_m的时空变化特征，对15个格网点2019年的逐小时T_m按春、夏、秋、冬分别求取均值，得图6所示的T_m时空分布图。图6中高程源于地理空间数据云(https://www.gscloud.cn/)提供的30 m × 30 m分辨率DEM数据。

由图6可看出，受贵州地形起伏大的影响，四个季节贵州T_m均呈现出明显的地域差异性，总体表现为贵州东部和南部区域高，而西部和北部区域低。春季、夏季、秋季、东季T_m的最大均值与最小均值间的差值分别为13.62 K、14.33 K、12.36 K和12.86 K。为更好地分析贵州T_m随高程和季节的变化，绘制图5所示的折线图。

由图6可看出，15个格网点各季节T_m均值序列与格网点高程密切相关，随高程的增加总体呈下降趋势。春季、夏季、秋季T_m均值序列与高程间的相关系数分别为−0.82、−0.95和−0.84，统计学上表现为极强相关，而冬季T_m均值序列与高程间表现为中等程度相关，相关系数为−0.46。此外，各格网点T_m均值季节上也表现出明显的差异性，T_m均值由高到低排列分别为夏季、春季、秋季和冬季。

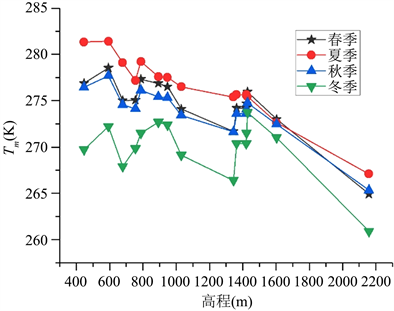
Figure 5. The relationship between T_m and elevation

图5. T_m与高程间的关系

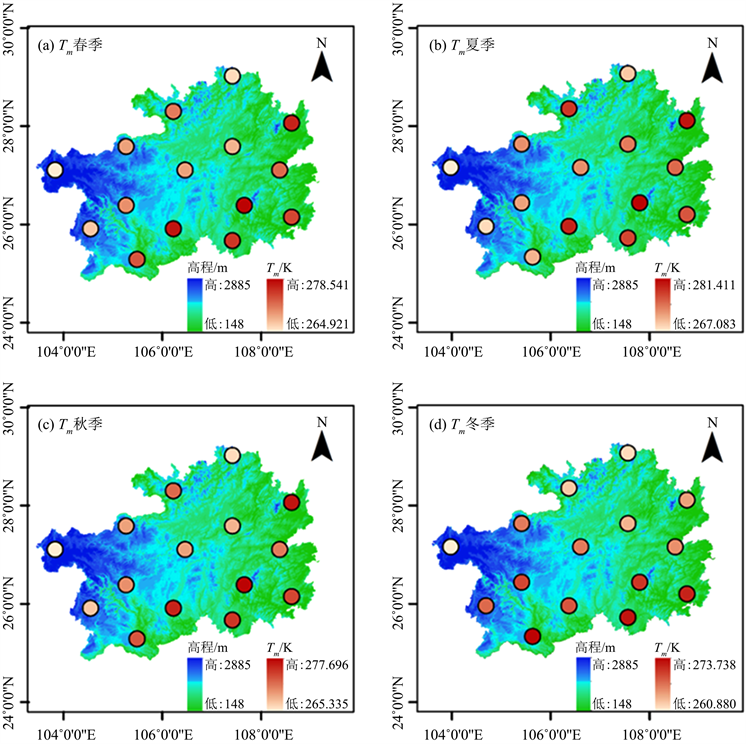
Figure 6. Temporal and spatial changes of T_m in Guizhou

图6. 贵州T_m时空变化

6. 结语

针对贵州地形起伏大、区域气候差异明显的特征，本文基于2011年~2018年共8年的高时空分辨率ERA5气象资料，在顾及T_m周期特性的基础上，建立了一种贵州本地化加权平均温度格网模型(GZTm)。通过对GZTm的精度评价和贵州T_m的时空变化特征分析，得出以下结论：1) 基于ERA5本地化气象资料所构建的GZTm模型，精度较Bevis公式和GPTm模型均得到了不同程度的改善，且GZTm具有更高的可靠性和稳定性；2) 贵州T_m季节差异性明显，15个格网点夏季与冬季T_m的最大差值和最小差值分别为11.60 K和1.61 K；3) 受贵州地形起伏大和区域性气候的影响，贵州T_m呈现出较强的区域差异性，四个季节不同格网点处T_m的最大差值均达到了12 K以上；4) 不同季节T_m与高程间的相关程度存在差异，相关系数由大到小排列依次为夏季 > 秋季 > 春季 > 冬季。

基金项目

国家自然科学基金项目(41901225、52064005)；贵州大学测绘科学与技术研究生创新实践基地建设项目(贵大研CXJD [2014] 002)。

NOTES

^*通讯作者。