非线性梁振动偏微分方程求解的L-稳定方法

L-Stable Method for Solving Partial Differential Equations of Nonlinear Beam Vibration

摘要: 基于高阶非线性梁振动偏微分方程的一般形式，构造了数值求解的L-稳定格式。首先，选取三角插值基函数，基于插值定理进行空间离散，将带有初边值条件的偏微分方程求解问题转化为微分–代数方程求解。然后在时间区间上构造L-稳定求解格式进行求解。以无轴向运动简支梁在外部激励下的强迫振动方程为例进行数值仿真，对梁的位移轨迹、边界条件及系统能量进行探究，并与龙格–库塔法、微分求积法进行对比，结果表明，L-稳定方法可以在较大步长下满足边界，位移轨迹与模型方程一致，在计算精度和稳定性上都有较好的体现。

Abstract: The general form of higher order nonlinear partial differential equation of beam vibration was given, and the solution method based on L-stable scheme was studied. Firstly, the triangular interpolation basis function was selected to discretize the space based on the interpolation theorem, and the problem of solving partial differential equations with initial boundary conditions was transformed into solving differential-algebraic equation. Then the L-stable solution scheme was constructed in the time interval. The forced vibration equation of a simply supported beam without axial motion subject to external excitation was taken as an example; the displacement trajectory, boundary conditions and system energy of the beam were studied, and compared with Runge-Kutta method and differential quadrature method. The results show that the L-stable method can satisfy the boundary conditions in large step size, the displacement trajectory is consistent with the model equation, and it has good performance in calculation accuracy and stability.

1. 引言

梁结构作为一种常见的工程结构，被广泛应用于房屋建设、桥梁工程、航空航天等领域。在实际生活中，梁自身容易受到外界因素的干扰而引起结构的振动，影响整体的稳定性，所以对梁振动问题的研究一直是人们关注的焦点。18世纪，文献 [1] 就简化线性弹性理论研究了梁的受力和变形问题，得到了Euler-Bernoulli梁方程。文献 [2] 研究了一维区间上非线性屈曲梁方程的初边值问题；文献 [3] 考虑刚体和柔性体运动相互作用的平移梁模型，推导出梁横向振动下的解析解，并在不同边界条件下验证了解析解的有效性；文献 [4] 针对轴向运动系统提出了一种简单的粘滞阻尼机制，研究了超临界转速范围内简支梁在横向激励下的动力学响应；文献 [5] 研究了两端固定轴向运动梁的横向振动，得到了固有频率和模态函数；文献 [6] 就弯曲和扭转联合作用下薄壁梁振动问题，研究了Sobolve空间中的一类非线性梁方程组的初边值问题；文献 [7] 考虑材料的不同拉压弹性模量，研究了铁木辛柯梁自由振动问题。上述研究中的模型方程多是一些高阶、非线性偏微分方程，在数值求解的精确性上研究较多，但在稳定性方面的研究还比较少。

L-稳定方法是一种基于Taylor展开研究数值稳定性的方法。文献 [8] 通过具有A-稳定的数值方法求解了刚性微分方程；文献 [9] 在此基础上进一步发展并将其应用到非线性模型方程；文献 [10] 构造了一类求解Stiff方程组的L-稳定高精度显示单步法；文献 [11] 针对刚性常微分方程组构造了L-稳定方法，该方法是二阶显式单步法；文献 [12] 通过W-变换构造了一类具有L-稳定和B-稳定的数值方法；文献 [13] 基于L-稳定的数值方法有效地抑制了求解过程中出现的高频振荡问题；文献 [14] 针对结构力学和多体系统动力学方程构造了L-稳定的块格式，分析了L-稳定块格式的精度；文献 [15] 提出了L-稳定实时协调算法的等效力控制方法并验证了其可行性。上述研究中，L-稳定方法多用于常微分方程与微分–代数方程稳定性问题的求解，尚未应用于求解梁振动这类高阶非线性偏微分方程。

文献 [16] [17] [18] 是求解梁振动方程的三种常见数值方法：有限差分法、有限元法、微分求积法(Differential Quadrature, DQ)，具有求解格式简单或精度较高等优点。本文基于微分求积法进行改进，将偏微分方程的初边值问题转化为微分–代数方程求解，并应用L-稳定求解格式，以简支梁振动方程为例进行数值仿真。

2. 数学模型

高阶非线性梁振动偏微分方程的一般形式可以表示为

$G\left(x,t,\mu ,D\mu ,\cdots ,D^k\mu ,\cdots \right)=0$ (1)

式(1)中， $\mu \left(x,t\right)$ 是2维的未知函数，其关于时间t的偏导数的最高阶为二阶，G是关于函数 $\mu$ 及其偏导数 $D\mu ,\cdots ,D^k\mu ,\cdots$ 的一个已知非线性函数， $D^k\mu$ 是 $\mu$ 的k阶偏导数： $D^k\mu ={\partial }^k\mu /\partial x^{k_1}\partial t^{k_2}$， $k_1+k_2=k$， $k_1,k_2\ge 0$ 是整数， $k_2=0,1,2$。

由文献 [19]，根据梁两端连接情况，可以将边界条件大致分为四类，分别为

两端固支：

$\mu \left(x,t\right)=0,\frac{\partial \mu }{\partial x}\left(x,t\right)=0,x=0,l$ (2)

两端简支：

$\mu \left(x,t\right)=0,\frac{{\partial }^2\mu }{\partial x^2}\left(x,t\right)=0,x=0,l$ (3)

两端滑支：

$\frac{{\partial }^3\mu }{\partial x^3}\left(x,t\right)=0,\frac{\partial \mu }{\partial x}\left(x,t\right)=0,x=0,l$ (4)

两端自由：

$\frac{{\partial }^3\mu }{\partial x^3}\left(x,t\right)=0,\frac{{\partial }^2\mu }{\partial x^2}\left(x,t\right)=0,x=0,l$ (5)

将边界条件看作约束函数 $\Phi ={\left[{\Phi }_1,\cdots ,{\Phi }_s\right]}^{\text{T}}\in R^{s\times 1}$，引入拉格朗日乘子 $\lambda ={\left[{\lambda }_1,\cdots ,{\lambda }_s\right]}^{\text{T}}\in R^s$，可以将带有简支边界条件的梁振动偏微分方程转化为指标-3微分–代数方程组：

$\{\begin{array}{l}G\left(x,t,\mu ,D\mu ,\cdots ,D^k\mu ,\cdots \right)+{\Phi }_{\mu }^{\text{T}}\lambda =0\\ \Phi ={\left(\begin{array}{cccc}\mu \left(0,t\right)& \mu \left(l,t\right)& \frac{{\partial }^2\mu }{\partial x^2}\left(0,t\right)& \frac{{\partial }^2\mu }{\partial x^2}\left(l,t\right)\end{array}\right)}^{\text{T}}=0\end{array}$ (6)

其中， ${\Phi }_{\mu }^{\text{T}}$ 是 $\Phi$ 关于 $\mu$ 的偏导数的转置，对 $\Phi$ 分别关于时间t求一、二阶导数得速度级约束 $\stackrel{\dot{}}{\Phi }$，加速度级约束 $\ddot{\Phi }$，令 $\stackrel{\dot{}}{\mu }=\partial \mu /\partial t$， $\ddot{\mu }={\partial }^2\mu /\partial t^2$，可以得到指标-2、指标-1的微分–代数方程组：

$\{\begin{array}{l}G\left(x,t,\mu ,D\mu ,\cdots ,D^k\mu ,\cdots \right)+{\Phi }_{\mu }^{\text{T}}\lambda =0\\ \stackrel{\dot{}}{\Phi }={\Phi }_{\mu }\left(\mu ,t\right)\stackrel{\dot{}}{\mu }+{\Phi }_t\left(\mu ,t\right)=0\end{array}$ (7)

$\{\begin{array}{l}G\left(x,t,\mu ,D\mu ,\cdots ,D^k\mu ,\cdots \right)+{\Phi }_{\mu }^{\text{T}}\lambda =0\\ \ddot{\Phi }={\Phi }_{\mu }\left(\mu ,t\right)\ddot{\mu }+{\left[{\Phi }_{\mu }\left(\mu ,t\right)\stackrel{\dot{}}{\mu }\right]}_{\mu }\stackrel{\dot{}}{\mu }+2{\Phi }_{\mu t}\left(\mu ,t\right)\stackrel{\dot{}}{\mu }+{\Phi }_{tt}\left(\mu ,t\right)=0\end{array}$ (8)

3. L-稳定方法

将区间 $\left[0,l\right]$ 离散为： $0=x_1<\cdots <x_{n+1}=l$。设函数 $\mu \left(x,t\right)$ 在 $\left[0,l\right]$ 上k阶可导，选取三角插值基函数，根据插值定理，通过求导运算，则函数 $\mu \left(x,t\right)$ 的k阶偏导数 $D^k\mu$ 可以表示为

$\left(\begin{array}{c}{D}^k\mu \left(x_1,t\right)\\ D^k\mu \left(x_2,t\right)\\ ⋮\\ D^k\mu \left(x_{n+1},t\right)\end{array}\right)=\left(\begin{array}{cccc}{A}_{1,1}^{\left(k_1\right)}& A_{1,2}^{\left(k_1\right)}& \cdots & A_{1,n\text{+}1}^{\left(k_1\right)}\\ A_{2,1}^{\left(k_1\right)}& A_{2,2}^{\left(k_1\right)}& \cdots & A_{2,n+1}^{\left(k_1\right)}\\ ⋮& ⋮& \ddots & ⋮\\ A_{n+1,1}^{\left(k_1\right)}& A_{n+1,2}^{\left(k_1\right)}& \cdots & A_{n+1,n+1}^{\left(k_1\right)}\end{array}\right)\left(\begin{array}{c}\frac{{\partial }^{\left(k_2\right)}\mu }{\partial t^{\left(k_2\right)}}\left(x_1,t\right)\\ ⋮\\ \frac{{\partial }^{\left(k_2\right)}\mu }{\partial t^{\left(k_2\right)}}\left(x_{n+1},t\right)\end{array}\right)$ (9)

这里， $A^{\left(k_1\right)}\in R^{\left(n+1\right)\times \left(n+1\right)}$ 是 $\mu \left(x,t\right)$ 关于 $x$ 的 $k_1$ 阶权系数矩阵，不同阶权系数矩阵之间满足递推公式：

$A_{i,j}^{\left(k_1\right)}={\displaystyle \underset{k=1}{\overset{n+1}{\sum }}{A}_{i,k}^{\left(1\right)}{A}_{k,j}^{\left(k_1-1\right)}}={\displaystyle \underset{k=1}{\overset{n+1}{\sum }}{A}_{i,k}^{\left(2\right)}{A}_{k,j}^{\left(k_1-2\right)}}=\cdots ={\displaystyle \underset{k=1}{\overset{n+1}{\sum }}{A}_{i,k}^{\left(k_1-1\right)}{A}_{k,j}^{\left(1\right)}},k_1>0,i,j=1,\cdots ,n+1$ (10)

在区间 $\left[0,T\right]$ 上取等分节点： $0=t_1<t_2\cdots <t_{m+1}=T$，步长设为 $h=t_{k+1}-t_k$， $k=1,\cdots ,m$。将式(9)、(10)代入式(7)，再进行降阶可得

$\{\begin{array}{l}\stackrel{\dot{}}{\mu }\left(x_i,t\right)=z\left(x_i,t\right)\\ G\left(x,t,\mu ,D\mu ,\cdots ,D^k\mu ,\cdots \right)+{\Phi }_{\mu }^{\text{T}}\lambda =0\\ \stackrel{\dot{}}{\Phi }={\Phi }_{\mu }\left(\mu \left(x_i,t\right),t\right)z\left(x_i,t\right)+{\Phi }_t\left(\mu \left(x_i,t\right),t\right)=0,i=1,\cdots ,n+1\end{array}$ (11)

在区间 $\left[t_k,t_{k+1}\right]$ 上取等分节点： $t_k<v_1<\cdots <v_r=t_{k+1}$，则有 $\mu \left(x,c_i\right)={\left[\mu \left(x_1,v_i\right),\cdots ,\mu \left(x_{n+1},v_i\right)\right]}^{\text{T}}\in R^{\left(n+1\right)\times 1}$， $z\left(x,c_i\right)={\left[z\left(x_1,v_i\right),\cdots ,z\left(x_{n+1},v_i\right)\right]}^{\text{T}}\in R^{\left(n+1\right)\times 1}$。设 $f\left(x,t\right)={\left[\mu {\left(x,t\right)}^{\text{T}},z{\left(x,t\right)}^{\text{T}},{\lambda }^{\text{T}}\right]}^{\text{T}}\in R^{\left(2n+s\text{+}2\right)\times 1}$， $f_i=f\left(x,v_i\right)\in R^{\left(2n+s\text{+}2\right)\times 1}$， $i=1,\cdots ,r$， $F={\left[f_1^{\text{T}},f_2^{\text{T}},\cdots ,f_r^{\text{T}}\right]}^{\text{T}}\in R^{r\left(2n+s\text{+}2\right)\times 1}$。由文献 [20]，根据Ehle定理及猜想，通过有理逼近构造L-稳定求解格式：

$F=a\otimes f_k+hb\otimes {\stackrel{\dot{}}{f}}_k+h\left(d\otimes I\right)\stackrel{\dot{}}{F}$ (12)

其中， $b\in R^{s\times 1}$， $d\in R^{s\times s}$， $a\in R^{s\times 1}$ 是全1矩阵， $I\in R^{\left(2n+s+2\right)\times \left(2n+s+2\right)}$ 是单位矩阵， $f_k=f\left(x,t_k\right)$， ${\stackrel{\dot{}}{f}}_k=\text{d}f/\text{d}t$， $\stackrel{\dot{}}{F}=\text{d}F/\text{d}t$， $\otimes$ 为Kronecker积。将式(12)代入式(11)，通过牛顿迭代得到 $\stackrel{\dot{}}{F}$，代入式(12)可得 $F$。

特别地，r = 4时，可得

$d=\frac{1}{4}\left(\begin{array}{cccc}\frac{431}{360}& -\frac{49}{60}& \frac{162}{360}& -\frac{73}{720}\\ \frac{46}{45}& \frac{4}{5}& -\frac{14}{45}& \frac{7}{90}\\ \frac{123}{120}& \frac{23}{20}& \frac{43}{120}& \frac{1}{240}\\ \frac{64}{45}& \frac{8}{15}& \frac{64}{45}& \frac{14}{45}\end{array}\right),b=\left(\begin{array}{c}\frac{197}{720}\\ \frac{37}{90}\\ \frac{91}{240}\\ \frac{14}{45}\end{array}\right)$ (13)

4. 数值算例

无轴向运动简支梁在外力作用下的振动方程为

$EI\frac{{\partial }^4\mu }{\partial x^4}+\rho A\frac{{\partial }^2\mu }{\partial t^2}=P\sin \left(\varpi t\right),0<x<l$ (14)

其中， $EI$ 为弯曲刚度， $\rho$ 为梁的质量密度，A为梁的横截面积， $P\sin \left(\varpi t\right)$ 为梁外载荷，l为梁的横长度。假定相关参数为

$\rho =1000\text{kg}/{\text{m}}^{\text{3}},A={10}^{-4}{\text{m}}^2,E=1.5\times {10}^8\text{N}/{\text{m}}^2,J=\frac{1}{6}\times {10}^8,P=100\text{N},\varpi =35\text{Hz},l=1\text{m}$

初始条件为

$\mu \left(x,0\right)=0,\frac{\partial \mu }{\partial t}\left(x,0\right)=0$

4.1. 梁振动方程时间历程图分析

图1是仿真时间为30 s，时间步长h = 0.01，空间节点选取7个切比雪夫节点，对指标-2方程求解得到的梁中点位移时程图；图2是对应的约束函数、速度级约束、加速度级约束误差时程图。可以看出，图1展示了简支梁在外激励作用下的来回往复运动轨迹，位移图像的不规则变化也体现了梁振动方程的非线性特征；图2的约束函数中的四个约束分量的误差量级都在10~12，这表示边界条件得到了较好地满足，其余约束的误差也很小，说明L-稳定方法在仿真过程中保持了良好的稳定性。

Figure 1. Time history diagram of beam midpoint displacement

图1. 梁中点位移时程图

Figure 2. Time history diagrams of constraint function and velocity level constraint and acceleration level constraint error

图2. 约束函数、速度级约束、加速度级约束误差时程图

4.2. L-稳定方法在不同参数下的结果比较

表1是仿真时间为30 s，空间节点选取7个切比雪夫节点，时间步长h = 0.01，不同指标方程下的对比结果。可以看出，指标-1方程在加速度级约束上误差最小，指标-2方程在速度级约束上误差最小，指标-3在约束函数上误差最小，这体现了不同代数约束对指标方程约束误差的影响；综合三种约束误差，指标-2方程对约束的满足程度更高。

Table 1. Comparison of indexes-1, -2, -3 solutions to differential algebraic equations with L-stable method

表1. L-稳定方法求解指标-1、-2、-3的微分–代数方程组的结果比较

表2是仿真时间30 s，空间节点为切比雪夫节点，时间步长h = 0.01，针对指标-2方程关于空间节点数目的结果比较：节点数取5时，无法求解，节点数从7开始，随着节点数增多，约束误差逐渐增大，运行时间延长，故而节点选取7时，求解时间最短，约束保持更好。

Table 2. Comparison of results of L-stable method with different space node numbers

表2. L-稳定方法在不同的空间节点数下的结果比较

表3是仿真时间30 s，空间节点选取7个切比雪夫节点，针对指标-2方程在不同时间步长下的结果比较：h = 0.1时，稳定性最好，运行时间最短，随着时间步长变小，各级约束误差虽然增大，但变化幅度较小，仍保持良好的稳定性。

Table 3. Comparison of results of L-stable method with different time steps

表3. L-稳定方法在不同时间步长下的结果比较

4.3. L-稳定方法与龙格–库塔法、微分求积法的结果比较

图3是仿真时间30 s，空间节点选取7个切比雪夫节点，时间步长h = 0.1，L-稳定方法与四阶龙格–库塔法(RK4)、DQ法的梁中点位移时程图，DQ法采用权系数修正处理边界条件。可以看出h = 0.1时，L-稳定方法仍能求得梁中点位移近似解，而另两种方法求解的结果发散，这体现了L-稳定方法在大步长下仍具有很好的求解精度，求解效果更好。

图4是时间步长为h = 0.01，空间节点选取7个切比雪夫节点，L-稳定方法与RK4法、DQ法(T = 1000 s)时仿真结果对比图。图5是相应条件下L-稳定方法的约束时间历程图。可以看出，L-稳定方法与DQ法求解结果较为接近，而RK4法求解结果差异稍大；在1000 s时，其约束误差较小，长时间仿真精度高，稳定性好。

Figure 3. Time history diagram of beam midpoint displacement of L-stable method, RK4 method and DQ method (h = 0.1)

图3. L-稳定方法与RK4法、DQ法的梁中点位移时间历程图

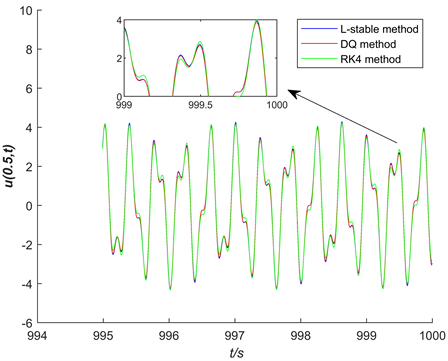
Figure 4. Comparison time history diagrams of beam midpoint displacement of L-stable method, RK4 method and DQ method (T = 1000 s)

图4. L-稳定方法与RK4法、DQ法的梁中点位移时间历程图(T = 1000 s)

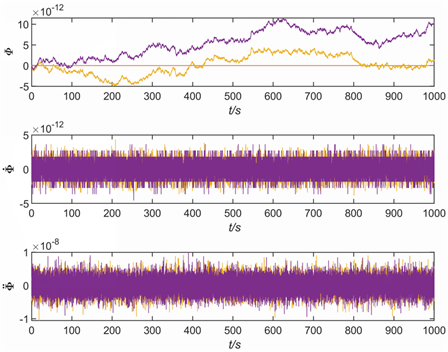
Figure 5. L-stable method constraint time history diagram (T = 1000 s)

图5. L-稳定方法约束时间历程图(T = 1000 s)

4.4. L-稳定方法与RK4法能量图分析

考虑去除外部激励，给定一个初始扰动：

$\mu \left(x,0\right)=0,\frac{\partial \mu }{\partial t}\left(x,0\right)=0.01x\left(1-x\right)$

图6是仿真时间30 s，空间节点选取7个切比雪夫节点，时间步长h = 0.01，L-稳定方法与RK4法总能量对比图。可以看出，L-稳定方法能量总体保持在一个较小的范围内，而RK4法的总能量随时间延长而逐渐增大，误差累积较大。

Figure 6. Comparison diagrams of total energy between L-stable method and RK4 method

图6. L-稳定方法与RK4法总能量对比图

5. 结论

本文针对高阶非线性梁振动偏微分方程的一般形式，基于插值定理进行空间离散，给出了偏微分方程求解的L-稳定格式。数值结果表明，L-稳定方法求解结果较好地展示了梁中点振动的非线性特征；针对指标-2方程，L-稳定方法的约束保持整体最优；时间步长对约束误差的影响较小，可以在大步长下满足各级约束；空间节点数目取7时稳定性最好；与RK4法、DQ法相比，在大步长下L-稳定方法求解精度更高，约束误差更小，同时长时间求解也能保持较高的计算精度和数值稳定性；忽略外部激励，给定初始扰动，L-稳定方法求解的系统总能量保持在一个较小的范围内，而RK4法的能量无法保持，误差累计较大。此方法构造原理简单，特别在边界处理上能更好地满足约束条件，后续可进一步加以改进，提高求解效率。

基金项目

国家自然科学基金(11772166, 12172186)。

NOTES

^*第一作者。

^#通讯作者。