高阶梁振动偏微分方程离散变分方法

Discrete Variational Method for Higher Order Beam Vibration Partial Differential Equation

摘要: 针对高阶梁振动偏微分方程这类求解问题，研究了离散变分方法。首先运用微分求积法离散空间，在时间区间上构造离散变分方法，对离散后的欧拉–拉格朗日方程进行变分。仿真实验运用MATLAB进行数值计算。以无轴向运动简支梁在外部激励下的强迫振动方程为例研究了插值基函数的种类、时间步长、插值节点类型与仿真时间等对求解的影响。数值结果表明，短时间内离散变分法的约束和能量稳定性优于经典龙格–库塔法；长时间仿真下，离散变分法的结果精度高于龙格–库塔法，并且可以很好地保持约束的稳定性。

Abstract: The discrete variational method is studied for the solution of high-order beam vibration partial differential equations. Firstly, the differential quadrature method is used to discretize the space, the discrete variational method is constructed on the time interval, and the Euler-Lagrange equation is variational. The simulation experiment uses MATLAB for numerical calculation. Taking the forced vibration equation of a simply supported beam without axial motion under external excitation as an example, the effects of the type of interpolation basis function, time step, interpolation node type and simulation time on the solution are studied. The numerical results show that the constraint and energy stability of the discrete variational method in a short time are better than those of the classical Runge-Kutta method; under long-time simulation, the accuracy of the discrete variational method is higher than that of Runge-Kutta method, and can maintain the stability of constraints.

1. 引言

梁振动方程在土木工程、电子、桥梁建设等领域有着广泛的应用 [1] [2]，该方程属于高阶偏微分方程，对梁振动方程精确稳定的数值求解具有重要意义 [3]。求解梁振动方程的数值方法有有限差分法、伽辽金方法、微分求积法等 [4]。微分求积法具有数学原理简单、易于实现和计算高效性等优点 [5] [6] [7]。王波和陈立群等 [8] 用微分求积法分析了在复杂边界下轴向变速黏弹性梁的稳态幅频响应，并和解析近似解进行对比。唐媛 [9] 应用微分求积研究在不同边界条件下梁的力学响应问题，分析了功能梯度参数对梁力学响应的影响。传统微分求积法在处理约束时对约束单独处理，约束的稳定性不能得到很好的保持。

为了提高精度和稳定性，在处理约束时把约束看作代数方程组，将偏微分方程转化为微分代数方程组，本文采用课题组的离散变分方法加以求解。近年来，离散变分方法已经在多体系统动力学中得到了广泛应用。其中，张冰冰和丁洁玉 [10] 对多体系统动力学的离散变分的数值方法进行了研究，以平面双连杆为例进行求解。于文洁 [11] 对经典的微分代数方程数值积分方法和现代几何数值积分方法进行了系统地调研，分析了不同方法的优缺点。离散变分方法尚未在偏微分方程中得到应用，因此对梁振动方程这类偏微分方程运用离散变分方法求解具有创新性和必要性。

本文主要介绍了梁振动方程的离散变分方法，通过观察长时间仿真下的时程图、约束变化，意在说明离散变分方法在长时间仿真下可以保持约束的稳定性。

2. 数学模型

2.1. 梁振动方程

考虑到梁的横向剪力与转动惯量时，由哈密顿原理得到梁振动方程 [12] 为

$\begin{array}{l}\rho A\ddot{u}-kGA\left(u_{xx}-{\psi }_x\right)-f=0\\ \rho I\ddot{\psi }-kGA\left(u_x-\psi \right)-EI{\psi }_{xx}=0\end{array}$ (1)

式(1)中空间坐标x和时间坐标t的范围是 $\left[0,l\right]$ 和 $\left[0,T\right]$，u为横向位移函数， $\psi$ 是转角函数，f是外部激励，并且都是关于x和t的函数，l为梁的长度，T表示运动总时间， $kA$ 是有效剪切面积，G是剪切模量， $\rho A$ 是线密度， $EI$ 是弯曲刚度， $\rho I$ 是转动惯量。

由(1)可得到在外部激励下梁振动方程 [12] 为

$EI\frac{{\partial }^{4}u}{\partial x^4}+\rho A\frac{{\partial }^{2}u}{\partial t^2}-\rho I\left(1+\frac{E}{kG}\right)\frac{{\partial }^{4}u}{\partial t^2\partial x^2}+\frac{{\rho }^{2}I}{kG}\frac{{\partial }^{4}u}{\partial t^4}=f+\frac{\rho I}{kGA}\frac{{\partial }^{2}f}{\partial t^2}-\frac{EI}{kGA}\frac{{\partial }^{2}f}{\partial x^2}$ (2)

式(2)中是梁振动方程的一般模型，时间和空间的最高偏导数为四阶，具有时间空间的二阶混合偏导数，梁的截面参数G，A和I关于x发生变化，u为横向位移函数，f是外部激励，并且都是关于x和t的函数。

在工程应用中梁的边界约束形式有简支、铰支连续、悬臂嵌固、两端嵌固 [13] 等情况，两端简支时为

${u|}_{x=0}=0,{\frac{{\partial }^{2}u}{\partial x^2}|}_{x=0}=0,{u|}_{x=l}=0,{\frac{{\partial }^{2}u}{\partial x^2}|}_{x=l}=0$ (3)

实际工程计算中，初始条件一般假设如下

${u|}_{t=0}=0,{\frac{\partial u}{\partial t}|}_{t=0}=0$ (4)

将边界约束写作代数方程组，把偏微分方程转化为微分代数方程组来求解，将x的区间 $\left[0,l\right]$ 离散成n个节点， $A_{i,j}$ 表示微分求积法的权系数矩阵 [14] [15]，约束方程组为

$\varphi =\left(\begin{array}{l}u\left(0,t\right)=0\\ u\left(l,t\right)=0\\ \frac{{\partial }^{2}u}{\partial x^{\text{2}}}\left(0,t\right)=0\\ \frac{{\partial }^{2}u}{\partial x^{\text{2}}}\left(l,t\right)=0\end{array}\right)=\left(\begin{array}{l}u\left(x_1,t\right)=0\\ u\left(x_n,t\right)=0\\ {\displaystyle \underset{j=1}{\overset{n}{\sum }}{A}_{1,j}^{\left(2\right)}u\left(x_j,t\right)}=0\\ {\displaystyle \underset{j=1}{\overset{n}{\sum }}{A}_{n,j}^{\left(2\right)}u\left(x_j,t\right)}=0\end{array}\right)$ (5)

3. 离散变分方法

3.1. 微分求积法离散

梁振动方程的动能、势能为

$T=\frac{1}{2}{\displaystyle \underset{0}{\overset{l}{\int }}\left(\rho I{\left(\frac{\partial \psi }{\partial t}\right)}^2+\rho A{\left(\frac{\partial u}{\partial t}\right)}^2\right)\text{d}x}$ (6)

$V={\displaystyle \underset{0}{\overset{l}{\int }}\left(\frac{EI}{2}{\left(\frac{\partial \psi }{\partial x}\right)}^2-\frac{kGA}{2}{\left(\frac{\partial u}{\partial x}-\psi \right)}^2-fu\right)\text{d}x}$ (7)

通过微分求积法离散后，带约束的拉格朗日函数为

$\begin{array}{c}L={\displaystyle {\int }_{t_i}^{t_{i+1}}\left(T-V+{\lambda }^{\prime }\varphi \right)\text{d}t}\\ ={\displaystyle \underset{t_i}{\overset{t_{i+1}}{\int }}(\frac{1}{2}\left(\rho I{\left(\frac{\partial \psi }{\partial t}\right)}^2+\rho A{\left(\frac{\partial u}{\partial t}\right)}^2\right)\text{d}t}-{\displaystyle {\int }_{t_i}^{t_{i+1}}\left(\frac{EI}{2}\left({\displaystyle \underset{j=1}{\overset{n}{\sum }}{A}_{i,j}}\psi \right)-\frac{kGA}{2}{\left({\displaystyle \underset{j=1}{\overset{n}{\sum }}{A}_{i,j}}u-\psi \right)}^2-fu\right)}+{\lambda }^{\prime }\varphi )\text{d}t\end{array}$ (8)

3.2. 离散变分方法

对约束方程组 $\varphi ={\left[{\varphi }_1,\cdots ,{\varphi }_s\right]}^{\prime }\in R^s$ 关于时间求二阶导，可得加速度约束函数 $\ddot{\varphi }$，对带约束的拉格朗日函数式(8)运用欧拉–拉格朗日方程组求变分，联立约束方程组式(5)，进而得到指标1的微分代数方程组 [16] 为

$\{\begin{array}{l}\rho A{\ddot{u}}_i=kGA\left({\left({\displaystyle \underset{j=1}{\overset{n}{\sum }}{A}_{i,j}}\right)}^2{u}_i-{\displaystyle \underset{j=1}{\overset{n}{\sum }}{A}_{i,j}}{\psi }_i\right)+f\\ \rho I{\ddot{\psi }}_i=kGA\left({\displaystyle \underset{j=1}{\overset{n}{\sum }}{A}_{i,j}}{u}_i-{\psi }_i\right)+EI{\left({\displaystyle \underset{j=1}{\overset{n}{\sum }}{A}_{i,j}}\right)}^2{\psi }_i\\ {\varphi }_q\ddot{q}=\eta ,\eta =-\left({\left({\varphi }_q\stackrel{\dot{}}{q}\right)}_q\stackrel{\dot{}}{q}+2{\varphi }_{qt}\stackrel{\dot{}}{q}+{\varphi }_{tt}\right)\left(i=1,2,\cdots ,n\right)\end{array}$ (9)

4. 数值算例

方程(2)中不考虑梁的横向剪力与转动惯量，外部激励f取为 $P\sin \left(\omega t\right)$ 。本文求解算例方程如下

$EI\frac{{\partial }^{4}u}{\partial x^4}+\rho {\rm A}\frac{{\partial }^{2}u}{\partial t^2}=P\sin \left(\omega t\right)$ (10)

式(10)中参数为 $E=1.5\times {10}^8\text{N}/{\text{m}}^{\text{2}}$， $I=1/6\times {10}^{-8}N/m^2$， $P=100\text{N}$， $\omega =35\text{Hz}$， $l=1m$， $\rho =1000kg/m^3$， $A={10}^{-4}{\text{m}}^2$，u为横向位移函数，是关于x和t的函数。微分求积法中空间插值节点数目为7，离散变分法中插值节点和高斯点数目均为2。边界条件和初始条件如下

$u\left(0,t\right)=0,\frac{{\partial }^{2}u}{\partial x^2}\left(0,t\right)=0,u\left(l,t\right)=0,\frac{{\partial }^{2}u}{\partial x^2}\left(l,t\right)=0,u\left(x,0\right)=0,\frac{\partial u}{\partial t}\left(x,0\right)=0$ (11)

4.1. 梁振动方程时间历程图

图1、图2是梁振动方程在步长 $h=0.001\text{m}$ 时龙格库塔法、离散变分法两种方法的运动轨迹时程图，龙格库塔法(Runge-Kutta method)简记为RK，离散变分法(Discrete variational method)简记为DV，图中的振动位置选为梁的中点，微分求积法中权系数矩阵分别选取三角插值基函数和拉格朗日插值基函数。仿真时间为0~30 s，选取图像在25~30 s进行对比。

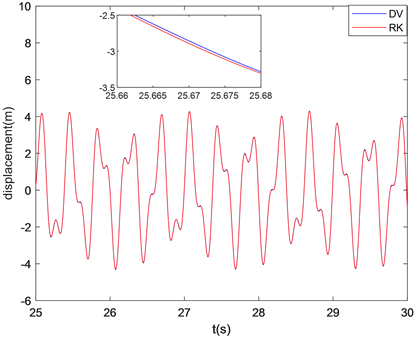
Figure 1. Time history diagram of vibration equation of beam with triangular interpolation

图1. 三角插值时梁振动方程的时程图

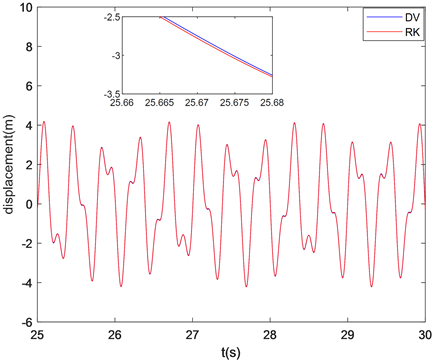
Figure 2. Time history diagram of vibration equation of beam with Lagrange interpolation

图2. 拉格朗日插值时梁振动方程的时程图

龙格库塔法作为一种求解常微分方程及微分代数方程组的经典方法，具有精度高，运行时间短的优点。图1、图2说明了在两种插值基函数下离散变分法和龙格库塔法的时程图像吻合程度高。这说明了离散变分法的时程图像精确程度高，证明了离散变分法在求解梁振动方程这类偏微分方程时的可行性。

图3、图4是梁振动方程在步长 $h=0.001\text{m}$ 时龙格库塔法、离散变分法、微分求积法(Differential quadrature method)，简记为DQ，三种方法的运动轨迹时程图，图中的振动位置选为梁的中点，微分求积法中权系数矩阵选取三角插值基函数，仿真时间为30 s和1000 s。30 s仿真时选取图像在25~30 s进行对比，1000 s仿真时选取图像在995~1000 s进行对比。

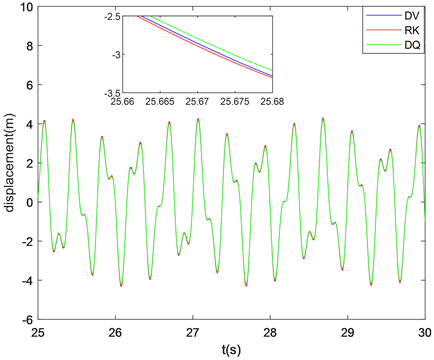
Figure 3. Time history diagram of beam vibration equation in 30 s simulation

图3. 30 s仿真时梁振动方程的时程图

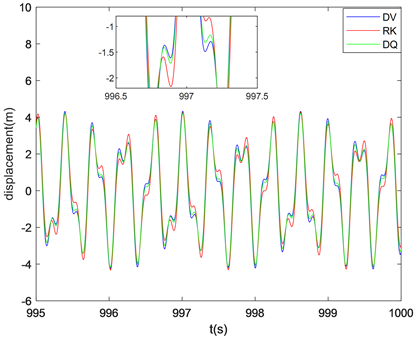
Figure 4. Time history diagram of beam vibration equation in 1000 s simulation

图4. 1000 s仿真时梁振动方程的时程图

从图3、图4可以看出，在步长及插值函数相同时，随着时间的增加三种方法的时程图结果相差变大，可以看出龙格库塔法长时间仿真的时程图精度更低，而离散变分法在长时间仿真下可以保持高精度，这是离散变分法的优越性。

4.2. 梁振动方程约束图

图5、图6是梁振动方程在步长 $h=0.001\text{m}$ 时龙格库塔法、离散变分法的4个约束方程的位移约束、速度约束、加速度约束变化图像，位移约束(Displacement Constraint)、速度约束(Speed Constraint)、加速度约束(Acceleration Constraint)分别用DC，SC，AC表示，微分求积法中权系数矩阵分别选取三角插值基函数，仿真时间为30 s进行对比。

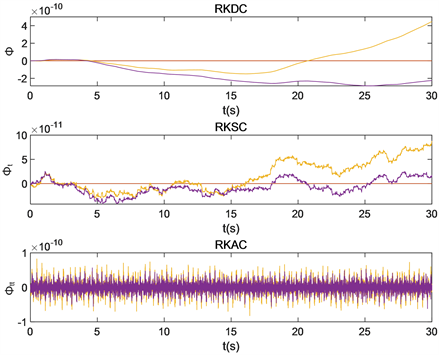
Figure 5. Constraint graph of Runge-Kutta method

图5. 龙格库塔法的约束图

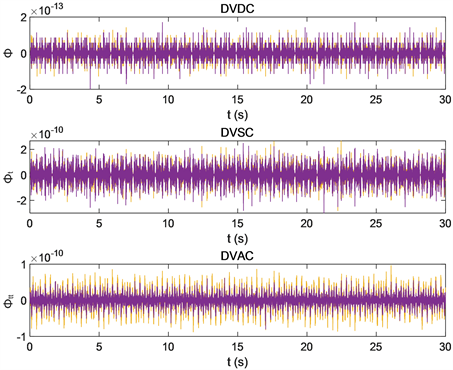
Figure 6. Constraint graph of discrete variational method

图6. 离散变分法的约束图

从上述图像可以看出，在插值函数相同时，龙格库塔法的位移约束、速度约束这两种约束违约，而加速度约束可以保持稳定。而离散变分法的三种约束均可以保持很好的稳定性，且位移约束量级上相比于龙格库塔法有明显的下降，这说明了离散变分法在保持约束方面的优越性。在插值函数不同时，三角函数插值的约束小于拉格朗日函数插值的约束。

表1是离散变分法在不同步长下的结果比较，仿真时间为30s，插值函数选为三角函数和拉格朗日函数。可以看出，随着步长减小，程序运行时间增大，三种约束均有所增大，因此可以看出离散变分方法适用于大步长。在插值函数不同时，三角函数插值的运行时间和约束要小于拉格朗日函数插值。

Table 1. Comparison of results of discrete variational method under asynchronous length

表1. 离散变分法在不同步长下的结果比较

从表2、表3可以看出龙格库塔法随步长的减小最大位移约束违约，最大速度约束、加速度约束保持稳定。离散变分法随步长的减小，三种约束均保持稳定，只有在 $h=0.001\text{m}$ 时最大速度约束有所增大。两种方法的速度约束、加速度约束相差不大，而离散变分法大幅度降低了梁振动方程的位移约束，可以看出离散变分方法在保持约束方面的优越性。

Table 2. Comparison of trigonometric interpolation results under different methods

表2. 三角函数插值下在不同方法下的结果比较

Table 3. Comparison of Lagrange interpolation results under different methods

表3. 拉格朗日函数插值下在不同方法下的结果比较

表4是三角函数插值下离散变分法取等距节点与非等距节点的结果比较。取 $h=0.01\text{m}$，仿真时间为30 s。可以看出，当离散变分法选择非等距节点时约束要小于取等距节点时的约束，其中切比雪夫节点综合精度较高。

Table 4. Comparison of results of different nodes under trigonometric function interpolation

表4. 三角函数插值下不同节点的结果比较

表5是离散变分法与龙格库塔法在不同时间下的结果比较。取步长 $h=0.01\text{m}$，微分求积法中权系数矩阵选取三角插值基函数，仿真时间选为30 s、100 s和500 s。可以看出随着时间的增加，离散变分法的三种约束均可很好的保持，而龙格库塔法的位移约束违约，这说明了离散变分法在长时间仿真下的优越性。

Table 5. Comparison of results of discrete variational method and Runge-Kutta method in different time

表5. 离散变分法与龙格库塔法在不同时间下的结果比较

4.3. 梁振动方程长时间仿真图

图7、图8是梁振动方程在运行时间 $t=10,000\text{s}$ 时龙格库塔法、离散变分法的4个约束方程的位移约束、速度约束、加速度约束的约束变化图像，微分求积法中权系数矩阵选取为三角插值基函数，选取 $h=0.01\text{m}$ 进行对比。

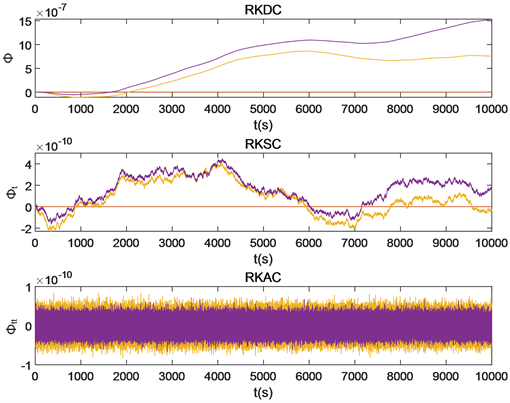
Figure 7. Long time simulation diagram of Runge-Kutta method

图7. 龙格库塔法求解的长时间仿真图

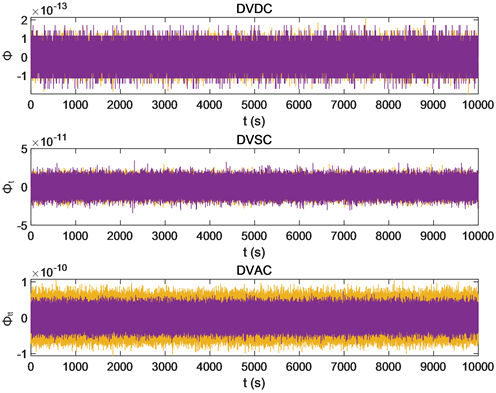
Figure 8. Long time simulation diagram of discrete variational method

图8. 离散变分法求解的长时间仿真图

从上述图像可以看出，龙格库塔法在长时间仿真下位移约束、速度约束违约，最大位移约束量级可达到10⁻⁶，只有加速度约束能够保持很好的稳定性。而离散变分法不但可以在长时间仿真下保持三种约束的稳定性，而且位移约束、速度约束的量级上也有下降，时间越长这种趋势越明显，这充分说明离散变分法在求解梁振动方程这类问题时的优越性。

5. 结论

本文针对高阶梁振动偏微分方程的一般形式，使用微分–代数方程求解方法，构造离散变分方法进行求解。数值结果表明，短时间内离散变分法与龙格库塔法的时程图结果接近，离散变分法的约束和能量稳定性高于龙格库塔法，长时间下离散变分法的时程图精度高于龙格库塔法，这说明了离散变分法的可行性和高效性。插值函数相同时，不同步长下的离散变分法的三种约束均能很好地保持，龙格库塔法的约束违约。步长固定时，三角插值的约束要低于拉格朗日插值。与经典Runge-Kutta法相比较，离散变分法数值精度更高，约束违约现象减弱，长时间仿真情况下三种约束保持效果更好。如何在保证约束的情况下应用到其他类型的偏微分方程，将是今后需要继续研究的内容。

基金项目

国家自然科学基金(11772166, 12172186)。

NOTES

第一作者。

^#通讯作者。