雅可比乘积公式在整数划分上的一个应用

An Application of Jacobi Triple Product Identity in Integer Partition Theory

摘要: 利用雅可比三重积公式和和欧拉公式，计算了五边形数和六边形数相关的一些无穷乘积和无穷级数。给出了一个关于两种整数划分具有相同个数的结果。

Abstract: Using Jacobi triple product identity and an Euler identity, some infinite products and series about pentagonal and hexagonal numbers are given. A result about two kinds of partition numbers is given.

1. 引言

欧拉的五边形数定理是整数划分理论中的一个经典定理，我们利用雅可比三重积恒等式和拉马努金乘积公式考虑把五边形数定理扩展到一般的n边形数并给出了一个新的整数划分公式。

2. 预备知识

对于正整数n与实数q，定义q-位移乘积：

${\left(a+x\right)}_q^n:=\left(a+x\right)\left(a+xq\right)\cdots \left(a+x{q}^{n-1}\right).$

以及无穷乘积

${\left(a+x\right)}_q^{\infty }:={\displaystyle {\prod }_{j=0}^{\infty }\left(a+x{q}^j\right)}.$

欧拉证明了以下两个著名公式：

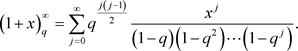(1)

$\frac{1}{{\left(1-x\right)}_q^{\infty }}=\underset{j=0}{\overset{\infty }{{\displaystyle \sum }}}\frac{x^j}{\left(1-q\right)\left(1-q^2\right)\cdots \left(1-q^j\right)}.$ (2)

在文献 [1] 中，G. E. Andrews使用上述两式和一些简单的代换，简洁地证明了Jacobi三重积恒等式：对于 $\left|q\right|<1$

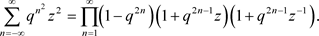(3)

在上式中做替换 $q\leftarrow q^{3/2}$ 以及 $z\leftarrow -q^{-1/2}$ 我们得到经典的欧拉五边形数定理：

$\underset{n\in Z}{{\displaystyle \sum }}{\left(-1\right)}^n{q}^{\frac{3n^2-n}{2}}=\underset{n=1}{\overset{\infty }{{\displaystyle \prod }}}\left(1-q^{3n}\right)\left(1-q^{3n-2}\right)\left(1-q^{3n-1}\right)=\underset{n=1}{\overset{\infty }{{\displaystyle \prod }}}\left(1-q^n\right).$ (4)

基本超几何函数 ${\Phi }_{\left(s,r\right)}$ 有如下定义：

${\Phi }_{\left(s,r\right)}\left[\begin{array}{llll}{a}_1\hfill & a_2\hfill & \cdots \hfill & a_r\hfill \\ b_1\hfill & b_2\hfill & \cdots \hfill & b_s\hfill \end{array};q,x\right]={\displaystyle {\sum }_{n=0}^{\infty }{\left({\left(-1\right)}^n{q}^{\frac{n\left(n-1\right)}{2}}\right)}^{s-r+1}}\frac{{\left(1-a_1\right)}_q^n{\left(1-a_2\right)}_q^n\cdots {\left(1-a_r\right)}_q^n}{{\left(1-b_1\right)}_q^n{\left(1-b_2\right)}_q^n\cdots {\left(1-b_s\right)}_q^n}\frac{x^n}{{\left(1-q\right)}_q^n}.$

当 $s=r=1$ 时，我们有拉马努金公式：对于固定的 $\left|q\right|<1,\left|a\right|>\left|q\right|,\left|b\right|<1,\left|b/a\right|<\left|x\right|<1$，

${}_1\Psi {}_1\left(a,b,;q;x\right)=\underset{-\infty }{\overset{\infty }{{\displaystyle \sum }}}\frac{{\left(1-a\right)}_q^n}{{\left(1-b\right)}_q^n}{x}^n=\underset{n=0}{\overset{\infty }{{\displaystyle \prod }}}\frac{\left(1-\frac{b{y}^n}{a}\right)\left(1-q^{n+1}\right)\left(1-\frac{q^{n+1}}{ax}\right)\left(1-ax{q}^n\right)}{\left(1-b{q}^n\right)\left(1-\frac{q^{n+1}}{a}\right)\left(1-\frac{b{y}^n}{ax}\right)\left(1-x{q}^n\right)}.$ (5)

在上式中令 $a=y,b=qy$，并且令 $x=y=z$，得到

${\displaystyle {\sum }_{m,n=0}^{\infty }{q}^{mn}{z}^{m+n}}-{\displaystyle {\sum }_{m,n=1}^{\infty }{q}^{mn}{z}^{-m-n}}={\displaystyle {\prod }_{n=1}^{\infty }\frac{{\left(1-q^n\right)}^2\left(1-z^{-2}{q}^n\right)\left(1-z^2{q}^{n-1}\right)}{{\left(1-z{q}^{n-1}\right)}^2{\left(1-z^{-1}{q}^n\right)}^2}}.$ (6)

文献 [2] 中，Farkas和Kra利用k-阶 $\theta$ 函数证明了五重积公式。文献 [3] 用统一的思路考虑了三重，五重，七重乘积公式，文献 [4] 使用基本的复变函数理论证明了上面的拉马努金公式，文献 [5] 利用西尔韦斯特的“伪几何论证”方法给出了三重积公式在有限情况下更加一般的结果，文献 [6] 考虑了雅可比乘积公式在数论中的解释，对于q-微积分一般的介绍可以参见文献 [7]。

3. 主要结果

我们的主要结果之一是如下公式：

定理一：

$\underset{n=1}{\overset{\infty }{{\displaystyle \prod }}}\frac{1-q^{4n-2}}{1-q^{2n-1}}=\underset{n=1}{\overset{\infty }{{\displaystyle \prod }}}\left(1+q^{4n-3}\right)\left(1+q^{4n-1}\right).$ (7)

定义序列

$P\left(m,n\right):=\frac{\left(m-2\right)n^2-\left(m-4\right)n}{2},m\ge 3,n\in Z.$

或者

$P\left(m,n\right)=\left(m-2\right)\frac{n\left(n-1\right)}{2}+n.$

当 $m=3$ 时，得到三角形数 $P\left(3,n\right)=\left\{10,6,3,1,0,0,1,3,6,10,\cdots \right\}$。

当 $m=4$ 时，得到平方数 $P\left(4,n\right)=\left\{25,16,9,4,1,0,1,4,9,16,25,\cdots \right\}$。

当 $m=5$ 时，得到五边形数 $P\left(5,n\right)=\frac{3n^2-n}{2}=\left\{40,26,15,7,2,0,1,5,12,22,35,\cdots \right\}$。

当 $m=6$ 时，得到六边数 $P\left(6,n\right)=2n^2-n=\left\{55,36,21,10,3,0,1,6,15,28,\cdots \right\}$。

当 $m=7$ 时，得到七边数 $P\left(7,n\right)=\frac{5n^2-3n}{2}=\left\{70,46,27,13,4,0,1,7,18,\cdots \right\}$。

当 $m=8$ 时，得到八边形数 $P\left(8,n\right)=\frac{n^2-4n}{2}=\left\{85,56,33,16,5,0,1,8,21,\cdots \right\}$。等等。

文献 [7] 已经讨论过三角形数和平方数的情况。

对于五边形数，我们考虑式(3)并做替换 $q\leftarrow q^{3/2},z\leftarrow q^{-1/2}$，得到：

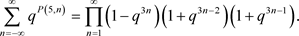(8)

把上式与式子(4)相比较，我们得到

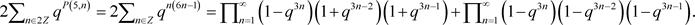(9)

以及

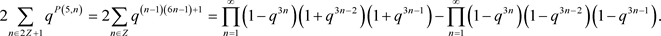
若我们在雅可比乘积中直接做替换 $q\leftarrow q^6,z\leftarrow q^{-1}$，可以得到

${\displaystyle {\sum }_{n\in Z}{q}^{n\left(6n-1\right)}}={\displaystyle {\prod }_{n\ge 1}\left(1-q^{12n}\right)\left(1+q^{12n-7}\right)}\left(1+q^{12n-5}\right).$ (10)

在雅可比乘积中，做替换 $q\leftarrow q^6,z\leftarrow q^{-7}$，可以得到

${\displaystyle {\sum }_{n\in Z}{q}^{6n^2-7n}}={\displaystyle {\prod }_{n\ge 1}\left(1-q^{12n}\right)}\left(1+q^{12n-13}\right)\left(1+q^{12n+1}\right).$ (11)

或者等价地

${\displaystyle {\sum }_{n\in Z}{q}^{\left(n-1\right)\left(6n-1\right)+1}}=q\left(q+1\right){\displaystyle {\prod }_{n\ge 1}\left(1-q^{12n}\right)}\left(1+q^{12n-1}\right)\left(1+q^{12n+1}\right).$ (12)

从而对于奇数项的或者偶数项的五边形数，我们总是可以将其展开成三种类型因子的无穷乘积或者这个这样的无穷乘积的和。

考虑在式子(6)中做替换 $q\leftarrow q^3,z\leftarrow q$，我们得到

${\displaystyle {\sum }_{m,n=0}^{\infty }{q}^{3mn+m+n}}-{\displaystyle {\sum }_{m,n=1}^{\infty }{q}^{3mn-m-n}}={\displaystyle {\prod }_{n=1}^{\infty }\frac{{\left(1-q^{3n}\right)}^2\left(1-q^{3n-2}\right)\left(1-q^{3n-1}\right)}{{\left(1-q^{3n-2}\right)}^2{\left(1-q^{3n-1}\right)}^2}}.$ (13)

在式子(8)中，考虑到

$\begin{array}{c}\underset{n\ge 1}{{\displaystyle \prod }}\left(1+q^{3n-2}\right)\left(1+q^{3n-1}\right)=\underset{n\ge 1}{{\displaystyle \prod }}\frac{\left(1-q^{6n-4}\right)\left(1-q^{6n-2}\right)}{\left(1-q^{3n-2}\right)\left(1-q^{3n-1}\right)}\\ =\underset{n\ge 1}{{\displaystyle \prod }}\frac{1-q^{6n-2}}{1-q^{3n-2}}\cdot \frac{\left(1-q^2\right)\left(1-q^8\right)\left(1-q^{14}\right)\left(1-q^{20}\right)\left(1-q^{26}\right)\cdots }{\left(1-q^2\right)\left(1-q^5\right)\left(1-q^8\right)\left(1-q^{11}\right)\left(1-q^{14}\right)\cdots }\\ =\underset{n\ge 1}{{\displaystyle \prod }}\frac{1}{1-q^{6n-1}}\underset{n\ge 1}{{\displaystyle \prod }}\frac{1-q^{6n-2}}{1-q^{3n-2}}\\ =\underset{n\ge 1}{{\displaystyle \prod }}\frac{1}{\left(1-q^{6n-1}\right)\left(1-q^{6n-5}\right)}.\end{array}$

从而可以得到五边形数另外一个无穷乘积：

(14)

下面我们考虑六边形数的幂次生成函数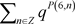，在雅可比乘积中做代换 $q\leftarrow q^2,z\leftarrow q^{-1}$ ：

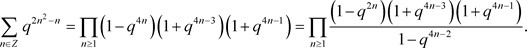
注意到对于三角形数，我们有，于是上式可以写成

${\displaystyle {\sum }_{n\in Z}{q}^{2n^2-n}}={\displaystyle {\sum }_{n\ge 0}{q}^{P\left(3,n\right)}}{\displaystyle {\prod }_{n\ge 1}\frac{\left(1-q^{2n-1}\right)\left(1+q^{4n-3}\right)\left(1+q^{4n-1}\right)}{1-q^{4n-2}}}.$

注意到任何一个六边形数都是三角形数，即对于 $n\ge 0$， $P\left(6,n\right)=P\left(3,2n-1\right)$， $P\left(6,-n\right)=P\left(3,2n\right)$，从而我们可以在两边消去公共因子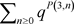得到

${\displaystyle {\prod }_{n\ge 1}\left(1-q^{4n-2}\right)}={\displaystyle {\prod }_{n\ge 1}\left(1-q^{2n-1}\right)}\left(1+q^{4n-3}\right)\left(1+q^{4n-1}\right).$ (15)

从而定理一得证。

定义：对于正整数n，假如有

$n=j+{\displaystyle {\sum }_{i=1}^j{m}_i},j\ge 1,m_i\ge 0,2i|m_i.$

则称 $\left(j,m_1,m_2,\cdots ,m_j\right)$ 属于n的第一类划分。

定义：对于正整数n，假如有有限个六元组 $\left(i,j,{\delta }_{ij},s,t,{\eta }_{st}\right)$ 满足关系

$n={\displaystyle {\sum }_{i,j}{2}^j}\left(4i-3\right){\delta }_{ij}+{\displaystyle {\sum }_{s,t}{2}^t}\left(4s-1\right){\eta }_{st},i,s\ge 1,j,t\ge 0,{\delta }_{ij},{\eta }_{st}\in \left\{0,1\right\}.$

则称这些六元组属于n的第二类划分。

定理二：对于任何正整数n，n的第一类划分的数目与第二类划分的数目相同。

证明：改写式子(15)成

$\underset{n\ge 1}{{\displaystyle \prod }}\frac{1}{1-q^{2n-1}}=\underset{n\ge 1}{{\displaystyle \prod }}\frac{\left(1+q^{4n-3}\right)\left(1+q^{4n-1}\right)}{1-q^{4n-2}}.$ (16)

应用替换 $q\leftarrow q^2$，可以得到

${\displaystyle {\prod }_{n\ge 1}\frac{1}{1-q^{4n-2}}}={\displaystyle {\prod }_{n\ge 1}\frac{\left(1+q^{sn-6}\right)\left(1+q^{8n-2}\right)}{1-q^{sn-4}}}.$

应用替换 $q\leftarrow q^4$，可以得到

${\displaystyle {\prod }_{n\ge 1}\frac{1}{1-q^{3n-4}}}={\displaystyle {\prod }_{n\ge 1}\frac{\left(1+q^{16n-12}\right)\left(1+q^{16n-4}\right)}{1-q^{16-8}}}.$

如此继续替换，把 ${{{\displaystyle \prod }}^{\text{}}}_{n\ge 1}\frac{1}{1-q^{4-2}},{{{\displaystyle \prod }}^{\text{}}}_{n\ge 1}\frac{1}{1-q^{2n-1}},{{{\displaystyle \prod }}^{\text{}}}_{n\ge 1}\frac{1}{1-q^{16n-8}},\cdots$ 全部代入式子(16)，我们得到

$\underset{n\ge 1}{{\displaystyle \prod }}\frac{1}{1-q^{2n-1}}=\underset{n\ge 1}{{\displaystyle \prod }}\left(1+q^{4n-3}\right)\left(1+q^{4n-1}\right)\left(1+q^{8n-6}\right)\left(1+q^{8n-2}\right)\cdots$ (17)

$=\underset{n\ge 1}{{\displaystyle \prod }}\underset{m\ge 0}{{\displaystyle \prod }}\left(1+q^{2^m\left(4n-3\right)}\right)\left(1+q^{2m\left(4n-1\right)}\right).$ (18)

利用欧拉公式(2)把上式左边进行展开，我们得到

${\displaystyle {\prod }_{n\ge 1}\frac{1}{1-q^{2n-1}}}={\displaystyle {\sum }_{j=0}^{\infty }\frac{q^j}{\left(1-q^2\right)\left(1-q^4\right)\cdots \left(1-q^{2j}\right)}}.$

把上面的式子右边分母中的每一项用几何级数进行展开，代入式子(18)，可以得到

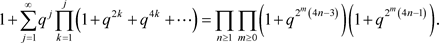(19)

然后我们比较两边q的相同幂次的系数，则定理得证。

例子：我们取 $n=7$，式子(19)左边 $q^n$ 的系数表示 的第一类划分的数目，右边表示其第二类划分的数目。考虑7的第一类划分：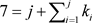

· $j=1$， $7=1+k_1=1+6$，满足条件。

· $j=2$， $7=2+k_1+k_2$， $k_1+k_2=5$，但我们要求 $2|k_1,4|k_2$，矛盾，故此种条件下没有满足条件的第一种划分。

· $j=3$， $7=3+k_1+k_2+k_3$， $k_1+k_2+k_3=4$，已知 $6|k_3$，所以有 $k_3=0$，而且有 $k_2=0$ 或者 $k_2=4$，所以有 $7=3+4+0+0=3+0+4+0$。

· $j=4$，与 $j=2$ 类似，不存在。

· $j=5$， $7=5+2+0+0+0+0$。

· $j=6$，不存在。

· $j=7$， $7=7+0+0+0+0+0+0+0$。

· 以上结果统计出7的第一种划分共有五种。

考虑第二种划分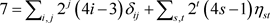。因为划分当中的每一项都是非负数，对于我们只需要考虑其中不大于7的项，总共有1，2，4，5这四个数，相应的对于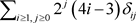不大于7的数只可能是3，6，7，于是，在这些数中间，每一个数至多选取一次，能够组成7的组合有

$7=7=1+6=2+5=3+4=1+2+4.$

共有五种。

结论：我们利用雅可比恒等式和拉马努金公式，得出了一些乘积展开式和一个关于整数划分的公式，这个公式的双射证明还有待探索。