1. 引言
很多在现实生活中的物理现象都可以在数学中通过建立模型来描述,然而这些模型往往都是非线性偏微分方程,难以用常规方法去解决,因此需要进行非线性偏微分方程精确解的研究,这些精确解的表达形式对解释这些物理现象可以起到非常好的作用,以及这些精确解的相关性质是非线性科学的重点。到目前为止,已经有很多简单有效的方法可以得到非线性偏微分方程精确解,如首次积分法、齐次平衡法、指数函数法、Riccati映射法、
展开法、Jacobi椭圆函数展开法等 [1] - [10]。本文主要运用Riccati映射法,选取了一类Riccati方程作为辅助函数,得到了广义KdV-mKdV方程 [11] 的精确解。
KdV方程已经是数理方程中的基本方程之一,1985年Korteweg和de Vries在讨论无黏不可压缩液体表面波动力学时引入此方程,随后在物理学与工程学的许多问题中,相继都引出KdV-mKdV方程。广义KdV-mKdV方程是等离子体物理、固体物理和量子场理论等领域中许多物理现象的重要非线性模型,它描述了一维非线性晶格中部分有界波在简谐力作用下的传播,特别描述了等离子体物理中无Landau阻尼的小振幅离子声波的传播 [12]。
广义KdV-mKdV方程为
(1)
其中,
均为常数。当参数取一些特定的值时,可以演化为KdV方程,mKdV方程以及其它一些重要的非线性发展方程。
2. Riccati映射法的介绍
对于一个非线性偏微分方程
(2)
我们假设它的解有如下形式
(3)
其中
满足
(4)
(4)解的情况如下
其中
都是任意常数,
为待求常数,最高次数m可以通过对最高阶导数项和最高阶非线性项运用齐次平衡理论来确定。将(3)、(4)代入(2),合并
的同次幂,并取各次幂系数为零,得到一组包含相关参数的非线性代数方程组,解出
,结合(4)解的情况代入(3)即可得到所求方程的精确解。
3. 广义KdV-mKdV方程的精确解
在(1)中,当
时,广义KdV-mKdV方程为
(5)
令
,所以
(6)
(7)
(8)
(9)
将(6)~(9)代入(5)可得
(10)
进一步地,(10)两边关于
积分可得
(11)
其中,
为积分常数。对(11)中的最高阶导数项
和最高阶非线性项
运用齐次平衡理论,(3)中的最高次数m满足等式
,解得
,假设(8)有如下形式的解
(12)
其中,
为待求常数。将(4)和(12)代入(11),合并
的同次幂,并取
的系数为零,得到包含相关参数的非线性代数方程组
解得代数方程组的非平凡解为
(13)
(14)
(15)
将(13)代入(12),我们可以得到8组广义KdV-mKdV方程的精确解
其中
,
是常数。为了研究广义KdV-mKdV方程的一些性质,我们选取一种简单的情形,取
,我们可以得到
以及8组解的图象,如图1。
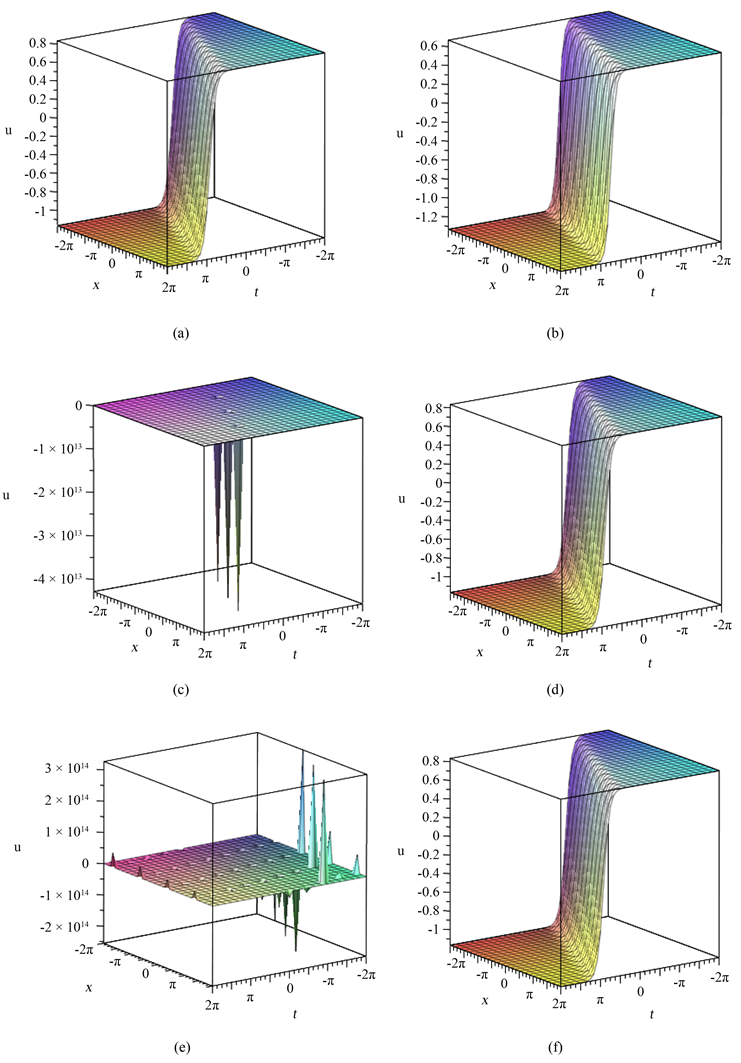
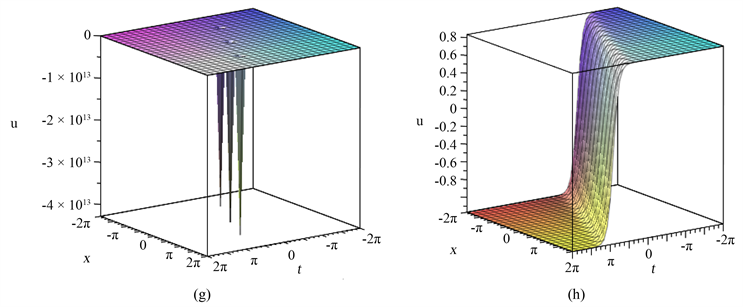
Figure 1. When
is the exact solution of the generalized KdV-mKdV equation, the waveform of
图1. 当
时广义KdV-mKdV方程的精确解
的波形图
再将(14),(15)代入(12),我们可以得到另外16组广义KdV-mKdV方程的精确解。
4. 结论
本文运用Riccati映射法求解了广义KdV-mKdV方程,得到了8组广义KdV-mKdV方程的精确解,同时取一种简单的情况,通过Maple软件得到了这些解所对应的图象。值得注意的是,本文研究的方程包含一大类非常重要的非线性偏微分方程,对图象的研究或许对物理上的应用将有一定的实际意义。