1. 引言
“信号与系统”是高等学校电子信息类专业的一门重要的专业基础课程 [1]。其中,采样定理是一个非常重要的教学内容。采样定理是1928年由美国电信工程师H.奈奎斯特首先提出来的,因此称为奈奎斯特采样定理。1933年由苏联工程师科捷利尼科夫首次用公式严格地表述这一定理,因此在苏联文献中称为科捷利尼科夫采样定理。1948年信息论的创始人香农对这一定理加以明确地说明并正式作为定理引用,因此在许多文献中又称为香农采样定理。采样定理说明了采样频率与信号频谱之间的关系,是连续信号离散化的基本依据,是信息论,特别是通讯与信号处理学科中的一个重要基本结论。然而,实际教学实践中,采样定理的教学效果却不尽如人意。许多高校教师从课堂、实验教学等方面进行了研究和探索 [2] [3]。本文从采样定理涉及到的工程问题出发,提出一个新的采样定理教学思路,希望通过更加贴近实际工程背景的教学组织来提高采样定理的教学效果。
2. 采样定理分析
时域采样定理:若时间连续信号
是频带有限的,其频谱上限为fm,则
可由其等间隔的样值点
唯一地表示。而采样间隔Ts必须小于1/2fm,或者说采样频率必须大于2fm。
在不同教材中,采样定理的具体表述会有些许的差异。但基本点有三个:1) 被采样信号必须是频带有限的;2) 采样间隔Ts必须小于1/2fm,或者说采样频率必须大于2fm;3) 可以用采样值
唯一表示
。或者说可以从满足条件的采样信号恢复原信号。对采样定理的理论解释基本上是将实际获得的
采样值
抽象成连续信号
与周期冲激序列
相乘得到冲激抽样信号
、也称为理想抽样信号,或者抽象为连续信号
与周期矩形脉冲
相乘得到矩形抽样信号
、也称为自然抽
样信号。而无论是理想抽样还是自然抽样,抽样信号
的频谱
都是原信号
频谱
的周
期延拓后的加权叠加
,其中权重
在理想抽样时是常数1/Ts、而在自然抽样时
是周期矩形脉冲信号的傅立叶级数系数。不难理解,只要采样频率fs大于2fm,则抽样信号
的频谱
中就不会出现原信号
频谱
混叠的现象,进而将抽样信号
通过一个理想低通滤波器便可以完全恢复原信号
。
3. 应用采样定理涉及到的工程问题
3.1. 抗混叠滤波器
从上一节采样定理分析可知,应用采样定理的前提是被采样信号的频带是有限的,或者说其傅里叶变换存在一个频率上限。然而,在工程实际中许多信号并不存在一个明确的频率上限,如周期方波、三角波等信号。即便对于具有明确频率上限的信号,考虑各种噪声干扰后,其实际频率上限也会增大许多。因此,在实际采样前信号都会经过一个低通滤波器来滤除信号中不需要的谐波成分和干扰噪声,以保证采样后的信号不会出现频谱混叠的现象。采样前的低通滤波器也称为抗混叠滤波器,其截止频率应大于有用信号的频率上限。
3.2. 实际采样频率的考虑
由采样定理分析可知,当采样频率大于原信号频率上限的两倍时,理想采样或自然采样信号就不会出现频谱混叠的现象,因此可以通过一个理想低通滤波器来恢复原信号。考虑到理想低通滤波器是物理不可实现的,而实际的低通滤波器都有一个过渡带,原信号频率上限两倍的采样频率是远远不够的,而且也不可能由采样信号无误差地恢复原信号。再考虑抗混叠滤波器实际的频率特性,如果采样频率仅仅是其截止频率的两倍,必然出现频谱混叠的现象。因此,实际确定采样频率需要考虑两个因素:一个是低通滤波器的实现,一个是恢复原信号时所容忍的误差。当所容忍的误差一定时,采样频率越高,低通滤波器的实现就越容易;当低通滤波器一定时,采样频率越高,所恢复的原信号的误差也就越小。
3.3. 由零阶采样保持信号恢复原信号
由采样定理分析可知,对于一个频带有限的信号来说,无论是冲激采样还是矩形脉冲采样,只要满足采样定理,都可以通过理想低通滤波器来恢复原信号。然而,在工程实际中我们既得不到冲激采样信号也得不到矩形脉冲采样信号,经过采样得到的是一系列离散的样值点
。现在的问题是如何利用这些样值点
来恢复原信号?
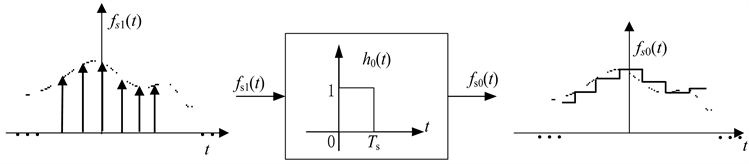
首先,在工程上容易根据抽样值
构成如图1(c)所示信号波形
,也称为零阶采样保持波形。为了从如图1(a)所示冲激采样信号
频谱得到
的频谱,构作一个线性时不变系统,它具有如图1(b)所示的冲激响应。
 (a) (b) (c)
(a) (b) (c)
Figure 1. (a) Impulse sampling signal; (b) System with rectangular impulse response; (c) Zero order sample and hold signal
图1. (a) 冲激采样信号;(b) 冲激响应为矩形脉冲的系统;(c) 零阶采样保持信号
显然,冲激采样信号
通过此系统便可得到如图1(c)所示
波形。即
因为门信号的傅里叶变换为
而冲激采样信号
的频谱为
所以,零阶采样保持信号
的频谱为
可以看出,零阶采样保持信号
的频谱的基本特征依然是原信号频谱
以
为周期重复,
但是要乘上
,此外还附加了一个延迟因子
。此时,在同样满足抽样定理的前提下要恢复
原信号频谱
,就需要引入如下具有补偿特性的低通滤波器 [4]
然而,与理想低通滤波器一样,上述具有补偿特性的低通滤波器也是物理不可实现的。事实上,当采样频率足够大、亦或要求不很严格的情况下,可以不加补偿,让
通过一个普通的低通滤波器即
可大致恢复原信号
。具体分析如下。首先,延迟因子
只是说明相对原信号有一个
的延时,并不会影响信号的波形。对信号波形产生实质影响的是
。取
,则当
时,
。也就是说,在
内,零阶采样保持信号的频谱
与原信号频谱
在幅值上最大误差仅为1.6% (参见图2)。因此,在采样频率远大于信号最高频率的条件下,让
直接通过一个普通的低通滤波器即可较好地恢复原信号
。
 (a) (b) (c)
(a) (b) (c)
Figure 2. (a) Original signal spectrum; (b) Impulse sampling signal spectrum; (c) Zero order sample and hold signal spectrum
图2. (a) 原信号频谱;(b) 冲激采样信号频谱;(c) 零阶采样保持信号频谱
4. 基于工程背景的采样定理教学组织
从以上对采样定理的理论剖析和涉及到的工程问题梳理可以看出,如果只注重理论分析而不涉及实际工程背景,则很难让学生深入理解采样定理并加以合理应用。因此,提出以下关于采样定理的教学组织流程,参见图3。
首先从用离散的样值点代表连续信号的角度提出两个问题:1) 最大采样间隔?2) 如何从样值点恢复连续信号?然后直接给出时域采样定理的表述来回答第一个问题。这样做的用意在于,落实学生对采样定理的正确理解。强调什么是信号的最大频率或频率上限。同时提出问题——为什么采样频率必须大于信号最大频率的两倍?由此,第三个模块给出采样定理的理论解释,即,从冲激采样和矩形采样信号的频谱说明频谱混叠和奈奎斯特采样频率的概念。引导学生注意到采样定理有三个关键前提:1) 被采样信号频带有限;2) 理想低通滤波器;3) 从冲激采样或矩形采样信号恢复原信号。由此进入第四个模块—采样定理涉及到的工程问题:1) 抗混叠滤波;2) 实际采样频率的考虑;3) 由零阶采样保持信号恢复连续信号。
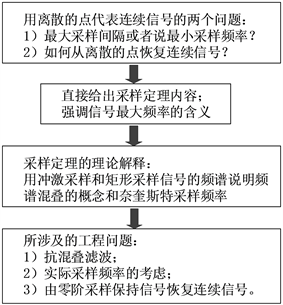
Figure 3. Teaching organization process of sampling theorem
图3. 采样定理的教学组织流程
5. 结语
采样定理是联系模拟世界与数字领域的一个桥梁,其重要性不言而喻。教学上,采样定理既需要深入的理论分析又涉及到具体的实际工程问题。本文分析了采样定理的理论基础,讨论了应用采样定理所涉及到的部分工程问题,提出了一个新的关于采样定理的教学组织方案。希望通过一个逻辑更加清晰、更加贴近工程背景的教学组织流程来改善采样定理的教学效果。