基于非负矩阵分解方法的主要城市环境质量状况分析

Analysis of Environmental Quality of Major Cities Based on Non-Negative Matrix Factorization

摘要: 根据水环境、大气环境、固体废物、声环境四方面的环境质量建立评价指标体系，利用非负矩阵分解方法对2020年全国31个主要城市的环境质量状况进行聚类分析评价。结果表明在2020年全国31个主要城市的环境质量状况中，环境质量状况在不同城市之间表现有差异，并且聚类结果呈现一定的空间分布特征。研究揭示了城市的环境质量状况与空间分布情况，能为城市生态环境状况发展建设提供参考。

Abstract: Establish an evaluation index system based on the environmental quality of water environment, atmospheric environment, solid waste, and acoustic environment, and use the non-negative matrix decomposition method to perform cluster analysis and evaluation on the environmental quality of 31 major cities across the country in 2020. The results show that in the environmental quality status of 31 major cities across the country in 2020, the environmental quality status varies between different cities, and the clustering results show certain spatial distribution characteristics. The research reveals the environmental quality and spatial distribution of the city, which can provide a reference for the development and construction of the urban ecological environment.

1. 引言

我国城市在实现中高质量发展的同时，资源枯竭、经济结构失衡、环境污染等社会问题频现，环境问题日益受到重视 [1]。2021年我国“十四五”规划指出，我国发展不平衡不充分问题仍然突出，重点领域关键环节改革任务仍然艰巨，生态环保任重道远。应当深入打好污染防治攻坚战，建立健全环境治理体系，推进精准、科学、依法、系统治污 [2]，不断改善空气、水环境质量，有效管控土壤污染风险，构建生态文明体系，推动经济社会发展全面绿色转型，建设美丽中国，以促进可持续发展 [3] [4] [5]。

本文通过建立反映环境质量状况的指标体系，运用非负矩阵分解方法，对2020年全国31个主要城市的环境质量状况进行了聚类分析评价研究，得出其环境质量状况分类与环境质量状况的影响因素，由此为城市环境污染治理与可持续发展提供科学依据。

2. 环境质量评价体系构建

本文旨在分析全国31个主要城市的环境质量情况，为更能充分考虑城市工业、农业、居民生活方面的环境状态，从水环境、空气环境、固体废物和声环境四个方面选取了与环境质量密切相关的16个指标 [6]，见表1。其中，指标选取包含工业源和城镇生活源两方面。

Table 1. Environmental pollution degree evaluation index system

表1. 环境污染程度评价指标体系

3. 数据处理与研究方法

3.1. 数据来源与处理

本文所有原始数据均来源于《中国统计年鉴2021》，由于各个指标间存在量纲上的不统一，在对数据进行非负矩阵分解聚类前，必须对数据进行处理，且各指标属于不同类型，有的指标的属性值越大越好(例如：一般工业固体废物综合利用量)，而有些指标的属性值越小越好(例如：工业化学需氧量排放量)，所以采用min-max标准化方法进行指标属性值的标准化，消除变量间在量纲和类型上的不同以及对聚类结果的影响。

对正向指标：

$X_i=\frac{x_i-x_{\min }}{x_{\max }-x_{\min }}$ (1)

对负向指标：

$X_i=\frac{x_{\max }-x_i}{x_{\max }-x_{\min }}$ (2)

3.2. 非负矩阵分解

聚类分析通过距离或相似性对数据进行分组，是数据探索、压缩和展现的重要工具。本文采用非负矩阵分解聚类分析方法对环境质量进行评价。聚类分析是依据研究对象的个体特征，对其进行分类的方法，指标之间高度相关性导致了传统聚类分析方法无法获得良好的分类效果，已有研究采用聚类分析进行评价多采用主成分聚类分析方法进行评价，但主成分方法其拟合结果未必能最有效地提取最优类别信息，进而影响到后续聚类分析效果 [7]。而聚类算法本质上可描述为矩阵分解问题，非负矩阵分解(Non-negative matrix factorization, NMF)是一种基于矩阵分解的降维手段，能实现高维的数据矩阵降维处理 [8]。

NMF的基本思想可以简单描述为：对于任意给定的一个非负矩阵X，NMF算法能够寻找到一个非负矩阵U和一个非负矩阵V，使得满足 $X\approx UV$，从而将一个非负的矩阵分解为左右两个非负矩阵的乘积 [9]。NMF是一种相对新颖的数据维度约简技术。它将非负性约束引入矩阵分解过程中，原始矩阵一般可分解为

$X=UV+E\approx UV$ (3)

其中， $X,U,V\ge 0$，假设阶矩阵，非负矩阵U和V分别为矩阵和矩阵，可分别视为基矩阵和权重系数矩阵。 $m\times n$ 的噪声矩阵E表示逼近误差，一般要求 ${\Vert E\Vert }_F$ 尽可能小并且快速收敛。r为矩阵X的秩，通常根据实际情况选取并满足 $\left(m+n\right)r<mn$，即利用少量的基向量便可表示高维数据。这意味着V可替代X，由此实现了对X的降维，进而获得反映数据本质特征的低秩矩阵U，UV能够近似拟合X。

3.3. 非负矩阵分解迭代算法

式(3)中提出的近似问题通常被表述为如下优化问题

$\underset{U,V\ge 0}{\min {\Vert X-UV\Vert }_F^2}$ (4)

该问题可以利用约束交替最小二乘法 [10] (Paatero和Tapper，1994)、乘法更新规则 [11] [12] (Lee和Seung，2001)、投影梯度方法 [13] (Hoyer, 2004)等算法求解。事实上，NMF算法可被解释为E服从不同概率分布假设下的最大似然算法。基于NMF的聚类特性，聚类中U解释为聚类中心矩阵，V反映聚类信息。

4. 31个主要城市环境质量评价

4.1. 基于NMF的聚类分析

本文研究的对象为全国31个主要城市，在水环境、大气环境、固体废物、声环境四方面，共16个指标，分析2020年各城市的环境质量状况。本文对反映2020年31个主要城市环境质量状况的数据整理标准化后，利用R完成非负矩阵分解的聚类分析。在NMF算法中，是通过随机初始U、V，开始的迭代算法，由于损失函数 $f\left(U,V\right)$ 可能有局部最小，所以不同的初始U、V可能会得到不同的结果，如果算法的结果收敛到一个比设定k更低的低秩，说明结果不是最优的，需要重新选择k值。NMF方法中判断rank重要的标准是cophenetic的大小，如图1，本文通过多次迭代计算cophenetic，获得最优k值为4。

给定矩阵X和一个参数K，NMF算法将高维的地区环境质量状况矩阵分解成一个系数矩阵U和一个基矩阵V。在基矩阵中，为第k类行为在第n个地区上的值。在系数矩阵中，为第m个地区中第k类指标的权重系数，则地区环境质量状况可视为地区多种指标线性加权的结果。同时，可根据权重系数进行聚类，当第k类行为的权重系数最大时，则认为该地区属于第k类，因此K也是聚类个数。

Figure 1. Determination of parameter K

图1. 参数K的确定

综上，选取k = 4，获取矩阵分解结果，即原始数据集聚类得到的簇数目为4，每个地区包含的属性项维数为4。

4.2. 环境质量状况矩阵分解

经过非负矩阵分解后，可得到维得基矩阵V和系数矩阵U，其中V是一个 $4\times 16$ 维的基矩阵，每一行代表一种环境质量状况(E1, E2, E3, E4)。

如图2，总体上看，每种环境状况都表现为有一个主要的指标，不同的状况突出的环境指标不同，E1在工业固体废物产生量、工业废物贮存量、工业二氧化硫排放量、工业氮氧化物排放量、工业烟(粉)尘排放量、生活二氧化硫排放量、生活氮氧化物排放量和生活烟尘排放量的值较高，主要反映了在E1环境质量状况中固体废物和大气环境的污染程度较高；E2在生活化学需氧量放量、生活氨氮排放量、工业固体废物贮存量、工业二氧化硫排放量、工业氮氧化物排放量和工业烟(粉)尘排放量的值较高，主要反映了在这类环境状况中，生活废水和大气环境中工业方面的影响是较严重的；E3水环境和大气环境中各项的指标值都较高，主要反映了在这类环境质量状况中，水污染和大气污染是较严重的；E4在工业固体废物综合利用量、工业固体废物贮存量、环境噪声等效声级、生活化学需氧量放量和生活氨氮排放量的值较高，主要反映在这类环境质量状况中，声环境和生活废水污染影响较大。

(a) E1 (b) E2 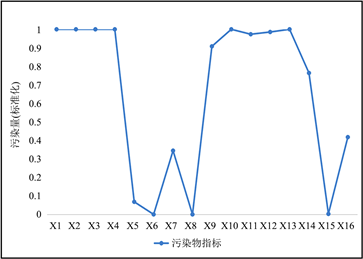(c) E3 (d) E4

Figure 2. Four environmental quality conditions

图2. 四种环境质量状况

U是一个 $31\times 4$ 维的系数矩阵，矩阵中的元素为每个城市在每种环境状况下行为(E1, E2, E3, E4)的权重系数，由权重系数最大值将城市分为4类，结果见表2。其中，第2类的城市数量最多，第4类次之，第1、3类相同。

Table 2. Clustering results of 31 major cities

表2. 31个主要城市聚类结果

4.3. 基于聚类分析的环境质量评价

通过非负矩阵分解得到全国31个主要城市的环境状况分类，从第一类到第四类的城市环境质量状况中，每一类都有不同的主要影响指标。为进一步说明聚类结果的空间布局，将聚类结果表示在地图上。

Figure 3. Spatial layout of clustering results

图3. 聚类结果的空间布局

观察图3可知，31个主要城市的环境质量状况分布特征总体表现出一定的区域特征，其中类别1主要集中分布在东南且呈现横线型结构，类别2和类别3主要分布在中西部及东北地区，而类别4则主要分布在东部地区，可以发现环境质量状况的分布和城市的地理分布具有一定的耦合性，反映了城市环境质量状况与城市发展行为、地理空间特征存在紧密的相互关联性。

5. 结论

基于31个主要城市环境数据和非负矩阵分解法对城市环境质量状况进行了聚类分析。研究发现：31个主要城市的环境质量状况受到的主要污染指标不同，形成不同的环境质量状况；且在空间上表现出明显的空间分布特征。结合各城市的发展行为，这与实际的城市发展情况较为吻合。说明通过非负矩阵分解方法进行聚类分析是可行的，并且对各城市在发展生态环境质量方面具有一定的参考价值，可结合城市自身的发展方式、空间地理位置有针对性地防治污染，对突出问题重点处理，实现城市经济、生态高质量发展。但是，本文研究数据仅局限于2020年，有待对更多年份数据进行研究，分析环境质量状况的时空分布特征，同时对环境质量状况的指标选取还可以继续探索，尽可能对环境质量状况详尽全面分析。