基于行车振动效应的预制装配式钢板组合梁桥行车舒适度研究

Research of the Comfort Level of Prefabricated Composite Steel Plate Beam Bridge Based on the Vibration Effect of Driving Vehicle

摘要: 预制装配式钢板组合梁桥是一种利用混凝土桥面板和钢主梁承担荷载的组合梁桥。该桥梁结构形式顺应行业发展趋势，在工程中得到了广泛应用。但由于车桥质量比相差较大，在行车荷载激励下容易引起桥梁振动，同时桥梁的振动会反作用于车辆，使行车舒适度降低。为此，本文拟采用一套液压阻尼装置，针对不同车速、桥面不平顺度等工况，对桥梁的动力响应进行研究与控制，以期提升行车舒适度。

Abstract: Prefabricated steel plate composite beam bridge is a composite beam bridge which uses concrete deck and steel girder to bear loads. The bridge structure conforms to the development trend of the industry and has been widely used in engineering. However, due to the large difference of vehicle-bridge mass ratio, the bridge vibration is easy to be caused under the driving load excitation. At the same time, the vibration of the bridge will react on the vehicle and reduce the driving comfort. Therefore, a set of hydraulic damper is proposed in this paper to control the dynamic response of the bridge under different vehicle speeds and roughness of the deck in order to improve driving comfort.

1. 引言

预制钢板组合梁桥是混凝土桥面板和钢主梁两种不同受力材料和构件形式的组合梁桥，利用在截面压缩区用高抗压强度的混凝土材料、截面拉伸区用高抗拉强度钢材的形式。充分发挥钢材和混凝土材料的优势，并通过连接件保证两种材料在连接处的协同工作 [1]。

与传统厚重的钢筋混凝土桥梁相比，钢板组合梁桥有着结构轻盈、快速装配、施工周期短、顺应行业发展趋势的特点。但同时，车辆质量与钢板组合梁桥质量比相差大，桥梁在车辆活载下易发生振动 [2]。剧烈的振动不仅影响桥梁结构的安全，致使结构疲劳受损，同时降低行车的舒适度体验。因此对钢板组合梁桥行车舒适度进行研究与控制是十分必要的。

本文以预制装配式钢板组合梁桥为对象，在车桥耦合振动理论的基础上研究不同行车工况组合下的桥梁振动效应，分析其行车舒适度，并与安装液压阻尼器后的行车舒适度对比，检验其效果。

2. 行车舒适度理论

行车舒适度是指车辆在行驶的过程中保持相对平稳，保证车辆的振动不会导致乘客感到不舒适的一种性能 [3]。在汽车行驶时，长时间处于振动环境中，人体也会感到疲劳、乏力，这对驾驶员来说，无疑是不舒适的，甚至是不安全的 [4]。

目前，国内外本研究领域内有很多种行车舒适度的评价方法，如：吸收功率法、UIC513评价方法、疲劳时间法、BS6841-1987 (英国标准)、Sperling平稳性指标法、等舒适度评价方法、ISO2631平顺性评价法，虽然学界中评价方法较多，但尚无一种方法是一致公认的 [5]。因此本文综合考虑各因素选取加速度干扰评价方法进行舒适度评价 [6]。

加速度干扰评价方法

车辆在道路上行驶容易受到道路自身线形、驾驶员操作技术以及道路的路况等级的影响，所以车辆在行驶的过程中车速是在不停变化的 [7]。为了能够描述车速在一定范围内的变化，20世纪50年代Hermann提出了加速度干扰的概念，并且将其定义为车辆加速度与平均加速度的标准差，即对车辆速度摆动的描述，用 $\delta$ 表示。并且通过研究测试得到了加速度干扰与行车舒适性之间的关系 [8]，如表1所示。

$\delta ={\left\{\frac{1}{T}{\displaystyle {\int }_0^T{\left[a\left(t\right)-\bar{a}\right]}^2\text{d}t}\right\}}^{\frac{1}{2}}$ (1)

$\bar{a}=\frac{1}{T}{\displaystyle {\int }_0^{T}a\left(t\right)\text{d}t}$ (2)

Table 1. The relationship between acceleration disturbance and driving comfort

表1. 加速度干扰与行车舒适性的关系

3. 工程概况

3.1. 桥梁参数

本文以一段长30 × 4 = 120 m的4跨连续钢板组合梁桥为例，桥面宽12 m，混凝土桥面板采用C50混凝土，钢主梁采用Q345D工字钢，桥梁相关截面参数如下图1所示。

(a) 钢板组合梁桥横截面 (b) 工字钢主梁横截面 (c) 横隔梁横截面

Figure 1. Basic cross-sectional parameters for steel plate combination girder bridge

图1. 钢板组合梁桥基本截面参数

钢板组合梁桥结构轻盈，桥梁在车辆活载下易发生振动，降低行车的舒适度体验。为此拟采用液压阻尼器提高桥梁舒适度，在距离桥梁支座3 m位置处以45˚安装液压阻尼器，两端分别与桥墩和钢梁下翼缘相连，每跨布置4组减振装置。

3.2. 阻尼器原理

液压阻尼器是一种减震装置，一般由缸体、活塞、阻尼孔、粘滞流体阻尼材料和活塞杆等部分组成，如图2所示，活塞在缸筒内作往复运动，活塞上有适量小孔成为阻尼孔，缸筒内装满粘滞流体阻尼材料。当活塞与缸筒之间发生相对运动时，由于活塞前后的压力差使流体阻尼材料从阻尼孔中通过，产生阻尼力，将结构振动的部分能量通过阻尼器中粘滞流体阻尼材料的粘滞耗能耗散掉，达到减小结构振动反应的目的。

Figure 2. Mechanism of hydraulic damper

图2. 液压阻尼器原理

3.3. 桥梁模型建立

采用ANSYS软件建立了精细化的钢板组合梁桥有限元模型，如下图3所示：混凝土桥面板采用SOLID65单元，工字钢主梁与横隔梁均采用SHELL43单元，工字钢主梁与混凝土面板之间的剪力连接件采用CONTA174单元与TARGE170单元模拟，模型共计7059个节点，7260个单元。

Figure 3. Finite element model of steel plate composite girder bridge

图3. 钢板组合梁桥有限元模型

为验证钢板组合梁桥有限元模型的正确性，利用Block Lanczos法进行模态分析，并提取前二阶振型进行分析，其动力特性参数如表2所示。实测的多座桥梁的1，2阶自振周期分别是0.35秒，0.10秒，由实测自振周期与Block Lanczos法提取的自振周期对比，可证明有限元模型的正确性。

Table 2. Bridge dynamic characteristics parameters

表2. 桥梁动力特性参数

3.4. 车辆模型

采用两车体三轴12自由度刚体模型，如图4所示，考虑轮对的沉浮，车体1与车体2的沉浮、侧滚、点头，共12个自由度，即车辆的自由度向量为 $d=\left[Z_{aL}^1,Z_{aR}^1,Z_{aL}^2,Z_{aR}^2,Z_{aL}^3,Z_{aR}^3,Z_{r1},{\varphi }_{r1},{\theta }_{r1},Z_{r2},{\varphi }_{r2},{\theta }_{r2}\right]$，利用d' Alembert principle可列出与6个轮胎相连的上部弹簧的压力为：

$F_{uL}^1=-K_{uL}^1\left(Z_{r1}+b{\varphi }_{r1}-L_1{\theta }_{r1}-Z_{aL}^1\right)-C_{uL}^1\left({\stackrel{\dot{}}{z}}_{r1}+b{\stackrel{\dot{}}{\varphi }}_{r1}-L_1{\stackrel{\dot{}}{\theta }}_{r1}-{\stackrel{\dot{}}{z}}_{aL}^1\right)$

$F_{uR}^1=-K_{uR}^1\left(Z_{r1}-b{\varphi }_{r1}-L_1{\theta }_{r1}-Z_{aR}^1\right)-C_{uR}^1\left({\stackrel{\dot{}}{z}}_{r1}-b{\stackrel{\dot{}}{\varphi }}_{r1}-L_1{\stackrel{\dot{}}{\theta }}_{r1}-{\stackrel{\dot{}}{z}}_{aR}^1\right)$

$F_{uL}^2=-K_{uL}^2\left(Z_{r1}+b{\varphi }_{r1}+L_2{\theta }_{r1}-Z_{aL}^2\right)-C_{uL}^2\left({\stackrel{\dot{}}{z}}_{r1}+b{\stackrel{\dot{}}{\varphi }}_{r1}+L_2{\stackrel{\dot{}}{\theta }}_{r1}-{\stackrel{\dot{}}{z}}_{aR}^2\right)$

$F_{uR}^2=-K_{uR}^2\left(Z_{r1}-b{\varphi }_{r1}+L_2{\theta }_{r1}-Z_{aR}^2\right)-C_{uR}^2\left({\stackrel{\dot{}}{z}}_{r1}-b{\stackrel{\dot{}}{\varphi }}_{r1}+L_2{\stackrel{\dot{}}{\theta }}_{r1}-{\stackrel{\dot{}}{z}}_{aR}^2\right)$

$F_{uL}^3=-K_{uL}^3\left(Z_{r2}+b{\varphi }_{r2}+L_4{\theta }_{r2}-Z_{aL}^3\right)-C_{uL}^3\left({\stackrel{\dot{}}{z}}_{r1}+b{\stackrel{\dot{}}{\varphi }}_{r1}-L_1{\stackrel{\dot{}}{\theta }}_{r1}-{\stackrel{\dot{}}{z}}_{aR}^1\right)$

$F_{uR}^3=-K_{uR}^1\left(Z_{r1}-Z_{aL}^3-b{\varphi }_{r2}+L_4{\theta }_{r2}-Z_{aR}^3\right)-C_{uR}^1\left({\stackrel{\dot{}}{z}}_{r1}-b{\stackrel{\dot{}}{\varphi }}_{r1}-L_1{\stackrel{\dot{}}{\theta }}_{r1}-{\stackrel{\dot{}}{z}}_{aR}^1\right)$

Figure 4. Vehicle dynamics model

图4. 车辆模型

以 $F_z$ 表示两个车体在球铰处的相互作用力(受压为正)，车体1的动力平衡方程为：

${\displaystyle \sum F_{r1}}=-F_z-g{M}_{r1}-M_{r1}{\ddot{z}}_{r1}-F_{uL}^1-F_{uR}^1-F_{uL}^2-F_{uR}^2=0$

${\displaystyle \sum I_{yz}^1}=-J_{yz}^1{\ddot{\varphi }}_{r1}+F_{uR}^{1}b-F_{uL}^{1}b+F_{uR}^{2}b-F_{uL}^{2}b=0$

${\displaystyle \sum I_{zx}^1}=-F_z{L}_5-J_{zx}^1{\ddot{\varphi }}_{r1}+F_{uR}^1{L}_1+F_{uL}^1{L}_1-F_{uR}^2{L}_2-F_{uL}^2{L}_2=0$

车体2的动力平衡方程为：

${\displaystyle \sum F_{r2}}=F_z-g{M}_{r2}-M_{r2}{\ddot{z}}_{r2}-F_{uR}^3-F_{uL}^3=0$

${\displaystyle \sum I_{yz}^2}=-J_{yz}^2{\ddot{\varphi }}_{r2}+F_{uR}^{3}b-F_{uL}^{3}b=0$

${\displaystyle \sum I_{zx}^2}=-F_z{L}_6-J_{zx}^2{\ddot{\varphi }}_{r1}-F_{uR}^3{L}_4-F_{uL}^3{L}_4=0$

3.5. 桥梁运动方程

将桥梁化为多自由度体系，将桥梁的运动方程以矩阵形式表示：

$M_b{\ddot{d}}_b+C_b{\stackrel{\dot{}}{d}}_b+K_b{d}_b=F_{bv}$

式中， $M_b$ 、 $C_b$ 和 $K_b$ 分别表示为桥梁的质量矩阵、阻尼矩阵和刚度矩阵； $d_b$ 为桥梁的位移矩阵； $F_{bv}$ 为车辆作用在桥面的作用力矩阵 [9]。

4. 动力响应控制及行车舒适度评价

将建立的有限元模型导入多体动力学软件UM对桥梁进行车桥耦合振动分析，研究桥梁的动力响应特性，通过液压阻尼器进行振动控制，并进行舒适度评价。

4.1. 车速影响

汽车在桥上行驶时，速度是一个重要参数，在不同速度下的车辆产生的车桥耦合作用有明显的不同，桥梁的动力响应也有所不同，这里通过改变车辆的速度来分析组合梁桥车桥动力响应及液压阻尼器减振效果随车速变化的一般规律。

4.1.1. 动力响应分析

选取具有代表性的低中高车速进行分析，即以车速分别为60 km/h、90 km/h、120 km/h的一辆载重汽车(不考虑路面不平顺)匀速行驶过四跨的连续梁桥为例，进行车桥耦合动力效应分析；取三者首跨竖向振动位移时程曲线及竖向振动加速度时程曲线如下图5~10所示：

Figure 5. Time-course diagram of nodal displacement in the first span of the bridge at 60 km/h

图5. 60 km/h车速下桥梁首跨跨中节点位移时程图

Figure 6. Time-course diagram of nodal acceleration in the first span of the bridge at 60 km/h

图6. 60km/h车速下桥梁首跨跨中节点加速度时程图

Figure 7. Time-course diagram of nodal displacement in the first span of the bridge at 90 km/h

图7. 90 km/h车速下桥梁首跨跨中节点位移时程图

Figure 8. Time-course diagram of nodal acceleration in the first span of the bridge at 90 km/h

图8. 90 km/h车速下桥梁首跨跨中节点加速度时程图

Figure 9. Time-course diagram of nodal displacement in the first span of the bridge at 120 km/h

图9. 120 km/h车速下桥梁首跨跨中节点位移时程图

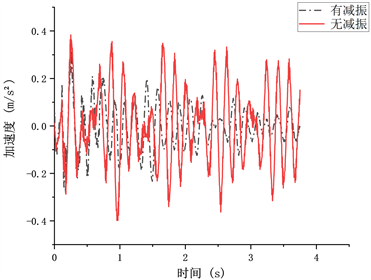
Figure 10. Time-course diagram of nodal acceleration in the first span of the bridge at 120 km/h

图10. 120 km/h车速下桥梁首跨跨中节点加速度时程图

取低中高车速三者的峰值位移与加速度干扰值，列下表进行减振前后对比：

Table 3. Summary of peak displacement and acceleration disturbance values at different vehicle speeds

表3. 低中高车速位移峰值及加速度干扰值汇总

综合低中高车速进行分析，组合梁桥动力响应主要表现为，随着车辆在桥上行驶，组合梁桥首跨跨中的竖向振动位移响应均表现为先增大后减小，在车辆匀速行驶至跨中位置附近时出现峰值竖向位移，驶过首跨后，位移响应明显降低，保持一定大小均匀波动；组合梁桥首跨跨中的竖向加速度响应均表现在最大加速度出现在首跨，车辆驶过首跨后，加速度总体减小，且通过其后三跨时，各跨之间的加速度无明显差异，总体走势基本一致。

由表3得出：从位移峰值、加速度干扰值数值上来看，并未体现出很强的规律性。但在施加液压阻尼器之后，低速(60 km/h)时，位移峰值绝对值由2.54下降为2.41，降低约5.12%，其加速度干扰值由0.0477下降为0.0337，降低约29.35%；中速(90 km/h)时，位移峰值由2.76下降为2.54，降低约7.97%，其加速度干扰值由0.1211下降为0.0899，降低约26.59%；高速(120 km/h)时，位移峰值绝对值由2.55下降为2.19，降低约10.20%，其加速度干扰值由0.1683下降为0.1299，降低约22.82%；在不同车速下，设置液压阻尼装置始终对位移峰值与加速度干扰值有一定的降低，即组合梁桥的振动响应得到舒缓与下降。

4.1.2. 不同车速下行车舒适度评价

对组合梁桥首跨跨竖向振动加速度时程曲线分析，拓展到10~150 km/h速度范围进行汇总，并利用上文所述评价方法，对不同车速条件下有无液压阻尼器桥梁的行车舒适度进行整体评价，如图11所示：

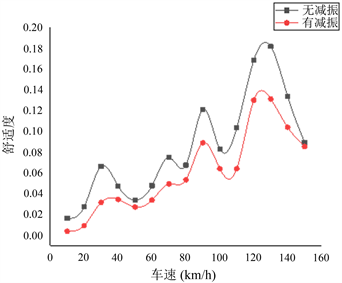
Figure 11. The relationship between driving comfort and speed curve

图11. 舒适度与车速关系曲线

从图11可得知，加速度干扰值并不是随着车速的增加而线性增大，而是随车速的整体变化呈现波动状况上升，在车速较小时，动力响应随着车速的增大而增大，当车速增大到某一特定值时，此时组合梁桥的动力响应达到较大，之后当车速继续增大时，组合梁桥的振动还来不及开始，车辆就已经驶出了桥面。在120~140 km/h速度范围内对桥梁的冲击作用最为明显出现，出现峰值。同时，从中可以看出，不同车速下行车设置液压阻尼装置的桥梁的加速度干扰值明显小于未设置液压阻尼装置的桥梁的加速度干扰值，尤其在峰值出加速度干扰值显著降低，行车舒适度提高显著。

4.2. 桥面不平顺度影响

当桥面存在不平顺时，车辆在其上行驶时会引起车身不同程度的振动，轻微的振动并不会引起乘客的不适，但当整个振动幅度到达一定程度时，乘客的不适感就会变得尤为明显。因此，同样需要考虑路面不平顺对桥梁动力响应的影响。

4.2.1. 动力响应分析

选取具有代表性的低中高桥面不平顺进行分析，即以桥面不平顺度分别为B、C、D的一辆载重汽车(车速控制在90 km/h)匀速行驶过四跨的连续梁桥为例，进行车桥耦合动力效应分析；取三者首跨竖向振动位移时程曲线及竖向振动加速度时程曲线如下图12~17所示：

Figure 12. Mid-span nodal displacement of the first span of a bridge under Class B roughness

图12. B级不平顺下桥梁首跨跨中节点位移

Figure 13. Mid-span nodal acceleration of the first span of a bridge under Class B roughness

图13. B级不平顺下桥梁首跨跨中节点加速度

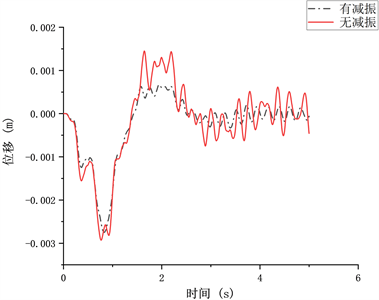
Figure 14. Mid-span nodal displacement of the first span of a bridge under Class C roughness

图14. C级不平顺下桥梁首跨跨中节点位移

Figure 15. Mid-span nodal acceleration of the first span of a bridge under Class C roughness

图15. C级不平顺下桥梁首跨跨中节点加速度

Figure 16. Mid-span nodal displacement of the first span of a bridge under Class D roughness

图16. D级不平顺下桥梁首跨跨中节点位移

Figure 17. Mid-span nodal acceleration of the first span of a bridge under Class D roughness

图17. D级不平顺下桥梁首跨跨中节点加速度

取低中高不平顺三者的峰值位移与加速度干扰值，列下表进行减振前后对比：

Table 4. Summary of different roughness displacement peaks and acceleration disturbance values

表4. 低中高不平顺位移峰值及加速度干扰值汇总

由表4得出：从位移峰值、加速度干扰值数值上来看，并未体现出很强的规律性。但在施加液压阻尼器之后，低不平顺(B)平顺时，位移峰值绝对值由2.70下降为2.47，降低约8.52%，其加速度干扰值由0.1370下降为0.0939，降低约31.46%；中不平顺(C)时，位移峰值绝对值由2.93下降为2.74，降低约6.48%，降低约8.52%，其加速度干扰值由0.1624下降为0.1122，降低约30.91%；高不平顺(D)时，位移峰值绝对值由3.44下降为3.00，降低约12.79%，其加速度干扰值由0.2199下降为0.1533，降低约30.27%；在不同不平顺下，设置液压阻尼装置同样始终对位移峰值与加速度干扰值有一定的降低，即组合梁桥的振动响应得到舒缓与下降。

4.2.2. 不同不平顺下行车舒适度评价

对组合梁桥首跨跨竖向振动加速度时程曲线分析，拓展到完全平顺至不平顺等级D范围进行汇总，并利用上文所述评价方法，对桥面不平顺条件下有无液压阻尼器桥梁的行车舒适度进行整体评价，如图18所示：

Figure 18. The relationship between driving comfort and road surface roughness curve

图18. 舒适度与路面不平顺程度关系曲线

从上述不同路面等级下桥梁行车舒适度曲线中可以看出，路面不平顺度对桥梁动力响应的影响很大，路面不平顺等级越高，产生的加速度干扰值越大，行车舒适性越差。

与此同时，加速度干扰值变化速率随着路面不平顺度等级的增大而增大，即不平度等级越高，加速度干扰值的增大越快。

同样的，不同路面等级下行车设置液压阻尼装置桥梁的加速度干扰值始终小于未设置液压阻尼装置桥梁的加速度干扰值。即无论何种路面等级，桥梁设置液压阻尼器始终会给行车舒适度带来有利影响。

5. 总结

通过比较加装液压阻尼器前后预制装配式钢板组合梁桥的动力响应与行车舒适度评价，可得以下结论：

1) 随着车速的增加，加速度干扰值并不是线性增大的，而是随车速的整体变化呈现波动状况上升。

2) 随着路面不平顺等级提高，桥梁加速度干扰值越大，行车舒适性越差。同时，不平度等级越高，桥梁加速度干扰值的增速越快。

3) 不同车速与路面不平顺工况下，设置液压阻尼装置的桥梁的加速度干扰值明显小于未设置液压阻尼装置的桥梁的加速度干扰值，对于减缓桥梁动力响应，提高行车舒适度具有积极意义。

4) 该装置对于工程中常见的工况类型具有较好的适应能力，能够有效提供竖向阻尼，显著降低桥梁跨中位移与加速度响应，提高预制装配式钢板组合梁桥行车舒适度。