基于FFT和波束空间MUSIC的快速超分辨算法

Fast Super-Resolution Algorithm Based on FFT and Beam Space MUSIC

摘要: MUSIC (Multiple Signal Classification)算法具有优良的估计精度和高分辨率，但是存在运算复杂、抗噪声性能差、无法对相干信号解相干等问题，因此难以广泛应用。文中将空域FFT测角融合到波束域MUSIC中，通过对阵列信号进行波束变换降低数据维度，结合空域FFT提供的先验信息为角度谱的峰值搜索提供搜索范围，从而有效地避免了角度谱中的栅瓣干扰、全谱搜索。该方案能够对单快拍数据进行快速角度估计，在降低传统超分辨方法运算量的同时，可以获得更稳健的性能。仿真结果表明，该方案的测角性能优于MUSIC算法，运算复杂度低于MUSIC算法，验证了该方案的有效性和优越性。

Abstract: The MUSIC algorithm has excellent estimation accuracy and high resolution, but it is difficult to be widely used because of its disadvantages such as complex operation, poor anti-noise performance and inability to conduct decoherence. In this paper, the spatial FFT Angle measurement is integrated into the beam domain MUSIC, and the data dimension is reduced by the beam transform of the array signal. According to the prior information provided by the spatial FFT, the search range is provided for the peak searching of the Angle spectrum, thus effectively avoiding the grid lobe interference and full spectrum searching in the Angle spectrum. The proposed scheme can be used to estimate the Angle of single snapshot data quickly, which can reduce the computation cost of the traditional super-resolution method and achieve more robust performance. The simulation results show that the performance of the proposed scheme is better than that of MUSIC algorithm, and the complexity is lower than that of MUSIC algorithm, which verifies the effectiveness and superiority of the scheme.

1. 引言

波达方向(Direction Of Arrival, DOA)的估计在雷达、声纳、电子对抗和移动通信等领域具有重要意义，最早关于DOA估计的方法是由傅里叶变换的线性谱引出的，该方法由于受空域“瑞利极限”的限制，很难达到对来波信号进行高分辨的估计，同时这些算法的抗噪性能较差，并没有获得满意的估计效果 [1] 。自Schmidt提出MUSIC (Multiple Signal Classification)算法 [2] 以来，超分辨阵列测向技术引起了广泛重视，MUSIC算法利用接收数据特征分解得到信号子空间和噪声子空间，通过信号子空间与噪声子空间的正交性构造谱函数进行角度谱峰值搜索来确定目标方位。它克服了传统基于常规波束形成方法的“瑞利限”问题，具有多信号同时测向、超分辨、测向精度高等特点。但在实用化方面，超分辨阵列测向技术仍存在一定的困难，主要表现在分辨信噪比门限高、运算复杂等方面。尤其是当阵列天线个数增加时，经典的超分辨MUSIC算法中自相关矩阵的维数也随着增加，导致计算量很大。

为弥补上述缺点，Bienvenu G.和Kopp L.提出了一种基于波束空间的高分辨目标DOA估计方法，该方法利用波束转换矩阵将阵元域输出数据转换到波束域输出，以波束输出作为信号处理的前级，然后进行高分辨DOA估计 [3] 。与阵元域相比，波束域的角度估计具有计算量小，分辨信噪比门限较低的优点 [4] 。波束域的高分辨方位估计方法可以充分利用目标的先验信息以及多波束系统的高稳健性，通过波束形成处理过程来降低高分辨方法的运算量，同时减少算法对误差的敏感程度，在工程应用中显示出比阵元域的高分辨方法更优越的统计特性 [5] 。

本文提出一种基于FFT和波束域MUSIC (Beam space MUSIC, B-MUSIC)的快速超分辨算法，B-MUSIC算法 [6] [7] [8] 对阵列接收数据进行预处理，通过线性变换把阵元空间合成一个或者几个波束，再对合成后波束域的数据用MUSIC算法估计角度。结合空域FFT提供的先验角度信息，为MUSIC角度谱搜索提供搜索范围，从而能够规避因为降维而引起的栅瓣干扰。为解决MUSIC算法无法对相干信源无法解相干和单快拍数据源的问题，将空间平滑融合到算法中，在波束形成前对阵列信号进行前后向平滑处理。此外，通过先验信息，在实际工程应用中，可以更加灵活地选择波束数量，并且还可以为信源估计提供先验信源个数，进一步提升信源估计的准确率。本文算法能够实现单快拍数据的快速角度超分辨，相较于MUSIC算法，具有更优的估计性能和更低的计算量，最后通过仿真验证了算法的有效性和优越性。

2. 信号模型及算法原理

2.1. 阵列信号模型

Figure 1. Signal model

图1. 信号模型

如图1所示，考虑M元均匀线阵(Uniform Linear Array, ULA)，阵元间距 $d=\lambda /2$ ，D个波长为 $\lambda$ 的远场窄带信号入射到该阵列，入射方向与阵列法线夹角定义为入射角度 ${\theta }_i$ ( $i=1,2,?,D$ )，则该阵列接收的单快拍数据矢量可表示为：

$x\left(t\right)=A\left(\theta \right)s\left(t\right)+n\left(t\right)$ (1)

$s\left(t\right)$ 表示 $D\times 1$ 维的入射信号向量， $n\left(t\right)$ 是相互独立的加性噪声向量， $A\left(\theta \right)=\left[a\left({\theta }_1\right),?,a\left({\theta }_D\right)\right]$ 是 $M\times D$ 维的阵列导向矩阵，由线性无关的阵列导向矢量 $a\left({\theta }_i\right)$ 组成的，阵列导向矢量定义为，

$a\left({\theta }_i\right)={\left[1,{\text{e}}^{j2\pi \frac{d\sin \left({\theta }_i\right)}{\lambda }},?,{\text{e}}^{j2\pi \left(M?1\right)\frac{d\sin \left({\theta }_i\right)}{\lambda }}\right]}^{\text{T}}$ (2)

2.2. 空域FFT测角

由图1可见，阵元1与阵元2接收到的信号波长为 $\lambda$ 的目标回波信号的传播路径差为 $\Delta R=d\sin \theta$ ，对应的相位差为 $\Delta ?=2\pi d\sin \theta /\lambda$ ，以此类推，到达各个阵元的信号，相对于第一个阵元的相位差为：

$\Delta ?=\left[0,2\pi \text{?}{f}_0\frac{d\sin \left(\theta \right)}{c},2\pi \text{?}{f}_0\frac{2d\sin \left(\theta \right)}{c},?,2\pi \text{?}{f}_0\frac{\left(N?1\right)d\sin \left(\theta \right)}{c}\right]$ (3)

目标的回波信号到达不同接收天线的传播路径长短不同，传播路径的长短与收发天线阵列间距以及目标的角度位置有关，而不同的传播路径长度又对应不同的相位息。因此可以利用目标频谱单元天线维的相位信息，根据已知的阵列间距估计得到目标的角度信息。

在某一时刻对所有阵元同时采样(称之为一个快拍)，将会得到M个数据点，将这M个数据点排列起来，对该数据进行FFT，得到包含角度信息的频谱图，进行局部峰值搜索，对峰值进行数学计算提取得到目标角度 $\theta$ 的信息。

2.3. 波束域MUSIC

B-MUSIC算法首先利用波束转化矩阵将阵元域输出数据转换为波束域输出数据，然后再进行MUSIC算法进行角度估计，算法原理图如图2所示，阵列输入数据如式(1)所示，设T为 $M\times B$ 维的波束转化矩阵，其中B为波束数目，则得到的波束域输出数据为，

$y\left(t\right)=T^{H}x\left(t\right)=T^{H}A\left(\theta \right)s\left(t\right)+n_B\left(t\right)$ (4)

式中 $n_B\left(t\right)=T^{H}n\left(t\right)$ 为波束域加性噪声。数据转换到波束域后，则波束域的方向矢量变为 $b\left(\theta \right)=T^{H}a\left(\theta \right)$ 。由(4)式得波束域的自相关矩阵为，

$R_B=E\left[y\left(t\right)y^H\left(t\right)\right]=T^{H}E\left[x\left(t\right)x^H\left(t\right)\right]T=T^{H}RT$ (5)

将阵列信号通过波束形成变换到波束域后，在波束域进行MUSIC算法估计角度，对相关矩阵 $R_B$ 进行特征值分解，D个较大的特征值对应的特征向量构成信号子空间， $M?D$ 个较小特征值对应的特征向量构成噪声子空间 $U_N$ ，根据噪声子空间构造角度谱函数，

$P_{\text{B-MUSIC}}=\frac{1}{b^H\left(\theta \right)U_N{U}_N^{H}b\left(\theta \right)}=\frac{1}{a^H\left(\theta \right)T{U}_N{U}_N^H{T}^{H}a\left(\theta \right)}$ (6)

Figure 2. Schematic diagram of beam space MUSIC [4]

图2. 波束空间MUSIC原理图 [4]

3. 基于FFT和B-MUSIC的快速超分辨算法

本文提出的基于FFT和B-MUSIC算法的快速超分辨算法，有效地结合了空域FFT和B-MUSIC算法的优点，能低复杂、高性能地实现单快拍阵列数据的角度估计。对阵列数据进行一次采样，用空域FFT算法进行快速、初略的估计，得到目标的先验信息。B-MUSIC算法在进行角度估计前需要对阵列信号进行线性变换，将阵元空间合成一个或几个波束，这种波束预处理的方法可以有效的降低数据维度，从而降低特征值分解的计算量。然而，如图3所示，这种处理方法也导致了空间角度谱的栅瓣干扰，严重影响空间角度谱的峰值搜索。由空域FFT算法得到的目标先验信息可以有效地解决该问题，在空间谱内以先验目标为中心，左右扩展形成一个局部的搜索范围，在空间谱中不再进行全局搜索，而是在空域FFT提供的搜索范围内进行局部搜索即可。该策略不仅能够规避栅瓣干扰，也进一步降低了峰值搜索的复杂度。此外，根据目标先验信息，B-MUSIC算法可以灵活的选择波束数量，为信源估计算法提供信源个数参考，进一步提升信源估计的准确率。

算法流程图如图4所示，在进行波束变换前，先对阵列信号进行前后向空间平滑 [9] ，具体推导可参

考文献 [9] ，平滑后的矩阵维度 $S=?2M/3?$ ，其中 $?\text{?}?$ 表示向下取整，得到平滑后的阵列空间相关矩阵，

$R=\frac{1}{2}\left(R_f+R_b\right)$ (7)

其中 $R_f$ 、 $R_b$ 分别表示前向、后向平滑矩阵， $R_b=J{\left(R_f\right)}^{*}J$ ，J是副对角线的元素都等于1，其余位置都是0的交换矩阵；*表示共轭操作。

Figure 3. Spatial angle spectrum of B-MUSIC

图3. B-MUSIC的空间角度谱

针对均匀线性阵列，文献 [8] 介绍了一种简洁的波束转换矩阵构成方法。 $M\times B$ 维度的波束转换矩阵T，表示为以下形式：

$T=\frac{1}{\sqrt{M}}\left[u\left(m\frac{2}{M}\right),u\left(\left(m+1\right)\frac{2}{M}\right),?,u\left(\left(m+B?1\right)\frac{2}{M}\right)\right]$ (8)

式中 $u\left(\eta \right)={\left[1,{\text{e}}^{j\pi \eta },{\text{e}}^{j2\pi \eta },?,{\text{e}}^{j\left(M?1\right)\pi \eta }\right]}^{\text{T}}$ 。

本文基于DFT波束变换矩阵方法，结合空间平滑方案，提出如下波束矩阵形成方案。首先构造一个包含所有波束的FFT矩阵，记为W，

$W\left(m,n\right)={\text{e}}^{\frac{?j2\pi }{M}nm},\text{?}n=0,1,2,?,S?1;\text{?}m=0,1,2,?,S?1$ (9)

对M维阵列数据x分段平滑，

$X_s=\left[x\left(1:S\right),x\left(2:S+1\right),?,x\left(M?S+1:M\right)\right]$ (10)

令矩阵 $A=W?X_s$ ，计算矩阵A中的各列功率和，选择其中最大的B个功率(B为波束数量，即降维后的维度)，记录其所在行号。相应的，在波束矩阵W中，按照该行号组成矩阵 $W_B$ ， $W_B$ 即为波束变换矩阵。

通过波束变换矩阵进行空域降维，将阵列域的数据变换到波束域，

$R_B=W_B?R?{\left(W_B\right)}^H$ (11)

之后的流程就与MUSIC算法的流程一致，对波束域相关矩阵进行特征值分解，并将特征值按顺序排列，采用信源估计算法进行信源个数估计。根据估计的信源个数划分信号子空间和噪声子空间，生成空间角度谱。根据空域FFT提供的搜索范围，进行局部峰值搜索，最后通过反三角函数计算提取角度 $\theta$ 信息。

Figure 4. Flow chart of fast super-resolution algorithm based on FFT and B-MUSIC

图4. 基于FFT和B-MUSIC的快速超分辨算法流程图

4. 仿真结果与分析

仿真构建了一个均匀的线性阵列，阵元个数 $M=32$ ，阵元间距 $d=0.5\lambda$ ，来自远场的信号入射角度为 $\theta$ ，相应的空间频率 $v=0.5\sin \theta$ 。信号源的幅度 $\left|\alpha \right|$ 根据所需的SNR进行设置，相位在 $\left[0,2\pi \right]$ 内均匀变化。噪声建模为均值为0，方差 ${\sigma }_n^2=1$ 的高斯噪声。对所有情况的仿真均进行5000次蒙特卡洛实验，从SNR与角度间隔两个方面比较本文算法与MUSIC算法的估计性能。本文算法中的波束数量设置为8，局部搜索范围以先验目标为中心，左右扩展8个空间谱点。

4.1. 算法的估计性能与SNR的关系

在本节中对算法的估计性能与SNR的关系进行了仿真分析，设置两个信号源，信号源幅度 $\left|{\alpha }_1\right|=\left|{\alpha }_2\right|$ ，电角度间隔设置为BW/2，其中 $BW=\left(2\pi /M\right)$ ，表示理论实孔径分辨率的二分之一，即两倍超分辨 [10] 。SNR在 $\left[?5\text{?}\text{dB},30\text{?}\text{dB}\right]$ 之间变化。本文算法与MUSIC算法的检测概率 [11] 和均方根误差(Root Mean Squared Error, RMSE)的仿真结果如图5，图6所示。

Figure 5. The relationship between detection probability of different algorithms and SNR

图5. 不同算法的检测概率与SNR的关系

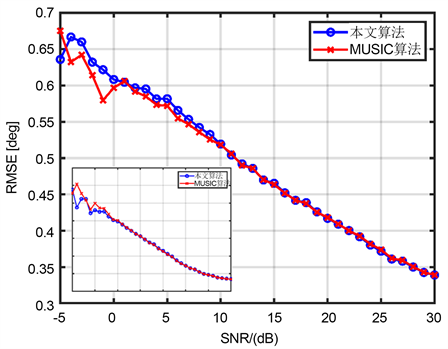
Figure 6. The relationship between RMSE and SNR of different algorithms

图6. 不同算法的RMSE与SNR的关系

如图5、图6所示，两倍超分辨下，本文算法与MUSIC算法性能接近。在信噪比 $\left[5\text{?}\text{dB},25\text{?}\text{dB}\right]$ 范围内，本文算法的检测性能略优于MUSIC算法，检测概率随着SNR的增加不断提升，本文算法达到80%以上的检测概率需要的信噪比为14 dB，在25 dB时检测概率可以达到100%。但是，在低信噪比 $\left[?5\text{?}\text{dB},10\text{?}\text{dB}\right]$ 范围内，本文算法对于目标角度值的估计误差高于MUSIC算法。

4.2. 算法的估计性能与角度间隔的关系

在本节中重点对算法的超分辨性能进行仿真，信噪比设为30 dB，设置两个信号源，幅度 $\left|{\alpha }_1\right|=\left|{\alpha }_2\right|$ ，信源1与信源2之间的电角度间隔由BW/5至2BW变化，探究算法对两个目标的分辨能力。

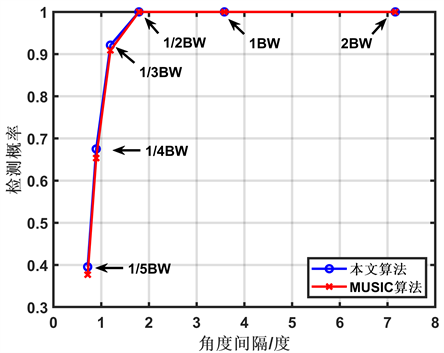
Figure 7. The relationship between detection probability and angle interval of different algorithms

图7. 不同算法的检测概率与角度间隔的关系

Figure 8. The relationship between RMSE and angle interval of different algorithms

图8. 不同算法的RMSE与角度间隔的关系

不同角度间隔下的检测概率和RMSE如图7、图8所示，在图中标注出了各角度间隔表示的超分辨能力。从图中可得，在高信噪比的条件下，MUSIC算法五倍超分辨至两倍超分辨的分辨成功率分别为：37.72%、65.36%、90.90%、100%；本文算法相应的检测概率分别为：39.56%、67.50%、92.12%、100%。在高信噪比下本文提出的算法对两个目标的分辨能力强于MUSIC算法，RMSE更小，估计值更加准确。

5. 复杂度分析

MUSIC算法的主要计算开销来源于相关矩阵的特征值分解和角度谱的峰值搜索，其中特征值分解的运算量为 $O\left(M^3\right)$ ，M为相关矩阵的维度。与阵元域MUSIC算法相比，本文提出的算法采用波束转换，降低了数据维度，并且通过引入空域FFT的先验信息，使得角度谱搜索不再进行全局搜索，而是仅仅对先验目标的子空间进行局部搜索即可。以上述仿真为例，阵元域MUSIC算法特征值分解的运算量为 $O\left({32}^3\right)$ ，空间谱搜索区间为 $\left[?{90}^{°},{90}^{°}\right]$ ；提出的算法降维后的维度 $B=8$ ，其特征值分解的运算量为 $O\left(8^3\right)$ ，而且空间谱搜索时，不再进行全谱搜索，而是仅仅搜索先验目标左右8个角度谱点的局部范围即可。因此，相较于阵元空间MUSIC算法，本文提出的算法总运算量降低。

6. 结论

在深入研究波束域的高分辨角度估计基本原理的基础上，提出了一种基于FFT和波束空间MUSIC的快速超分辨算法，通过FFT空域测角的先验信息有效地解决了波束域MUSIC角度谱的栅瓣干扰问题，有效地保留了MUSIC算法的超分辨性能，并且通过波束域降维和局部搜索大大地降低了MUSIC算法的计算量。通过理论分析和仿真验证了该方案的有效性和优越性。