基于KL不等式求解压缩感知问题

Solving Compressed Sensing Problem Based on Kurdyka-?ojasiewicz Inequality

摘要: 压缩感知问题在雷达探测、信号与图象处理、组合优化、金融等诸多领域中有着非常广泛的应用。本文将压缩感知问题在一定的条件下转化为等价的无约束问题。通过研究这类无约束问题的KL (Kurdyka-Łojasiewicz)性质，本文采用BB步长，应用相应的非单调线搜索的方法求解这类非线性函数的收敛性和线性收敛速率。

Abstract: Compression sensing problem is widely used in radar detection, signal and image processing, combination optimization, finance and many other fields. In this paper, the compressed sensing problem is transformed into an equivalent unconstrained problem under certain conditions. By studying the Kurdyka-Łojasiewicz (KL) properties of such unconstrained problems, we use BB steps to solve the linear convergence and linear convergence rate of such nonlinear functions.

1. 引言

Donho、Candes和Tao等人 [1] 在研究高度欠定的核磁共振成像问题时，正式提出了压缩感知的概念。压缩感知，也被称为压缩传感，它的基本思想是利用特定的矩阵，将K-稀疏的高维信号空间变换为低维信号空间，利用稀疏性信号的先验条件，通过某个线性或者非线性重建模型重建原始信号。压缩感知理论广泛应用于雷达探测、图像处理、无线传感网络等很多领域。压缩感知问题的求解备受关注。

压缩感知问题的模型如下：

$\begin{array}{l}\min \text{}\text{}\text{}{\Vert x\Vert }_0\\ \text{s}\text{.t}\text{.}y=Ax，\end{array}$ (1)

其中，A代表 $m\times n$ ( $m\ll n$ )的观测矩阵，x表示原始信号，且 $x\in {ℝ}^n$，y代表观测值，且 $y\in {ℝ}^m$。 ${\Vert x\Vert }_0$ 表示向量x的零范数(即非零元的个数)。求解问题(1)，需要列出x中所有非零位置的线性组合，有 $C_n^k$ 种。问题(1)的数值计算很不稳定，并且是一种NP (Nondeterministic Polynomially)难的非凸优化问题。具有代表性的求解方法有匹配追踪(MP) [2]，正交匹配追踪(OMP) [3]，稀疏自适应匹配追踪(SAMP) [4] 等。Donohoh、Candes和Tao等人在文献 [5] 中将其转化成与之等价的 $l_1$ 范数进行求解，证明了若观测矩阵A满足RIP (Restricted Isometry Property)，那么问题(1)与 $l_1$ 范数问题等价，并且建立了问题(1)的等价形式如下 [6]：

$\begin{array}{l}\min \text{}\text{}\text{}{\Vert x\Vert }_1\\ \text{s}\text{.t}\text{.}y=Ax。\end{array}$ (2)

本文用罚函数法，将问题(2)转化为与其同解的无约束问题：

$\underset{x\in R^n}{\min }\left\{f\left(x\right):=\frac{\lambda }{2}{\Vert Ax-y\Vert }^2+{\Vert x\Vert }_1\right\}$，

其中， $\lambda >1$。

KL不等式作为收敛性分析中的一个重要研究工具，并且应用广泛。像半代数函数、tame函数、向量范数等等都是KL函数。早在1963年S. Łojasiewicz [7] 在实分析函数中，研究一般的最速下降曲线问题解的轨迹是否为有限长度时，提出Łojasiewicz不等式：

$\Vert \nabla F\left(x\right)\Vert \ge c{\left|F\left(x\right)\right|}^{\theta }$， $\forall x\in U\left(\bar{x}\right)$，

其中， $F:{ℝ}^n\to ℝ$ 的实解析函数， $\bar{x}\in F^{-1}\left(0\right)$ 为临界点且 $\theta \in \left[\frac{1}{2},1\right)$， $c>0$。并由此推导出最速下降曲线

的解的轨迹是有限长度，有界轨迹收敛到临界点。随后，Kurdyka [8] 将这一结果扩展到可在o-minimal结构中定义的可微函数中，相应的广义不等式称之为KL不等式。本文主要建立与其同解的无约束优化问题模型的KL性质，从而设计基于BB (Barzilai-Borwein)步长线搜索算法。

2. 预备知识

对于给定的广义实值函数 $f:X\to \left(-\infty ,+\infty \right]$，若

$\text{dom}f:=\left\{x\in X|f\left(x\right)<\infty \right\}\ne \varnothing$，

则称 $f\left(x\right)$ 是正常的。对给定的 $\alpha \in ℝ$ 与 $\beta \in ℝ$，记

$\left[\alpha \le f\le \beta \right]:=\left\{x\in X|\alpha \le f\left(x\right)\le \beta \right\}$。

对于给定的 $\bar{x}\in X$ 和 $\delta >0$， $B\left(\bar{x},\delta \right)$ 表示以 $\bar{x}$ 为中心， $\delta$ 为半径的闭球。x到S的距离定义为

$\text{dist}\left(x,S\right):=\inf \left\{\Vert y-x\Vert :y\in S\right\}$。

定义1 [9] (Kurdyka-Łojasiewicz性质)设 $f:X\to \left(-\infty ,+\infty \right]$ 是正常的下半连续的函数。考虑任意 $\bar{x}\in \text{dom}\partial f$。若存在常数 $\eta \in \left(0,+\infty \right]$，满足如下条件的连续凹函数 $\phi :\left[0,\eta \right)\to {ℝ}_{+}$ ：

1) $\phi \left(0\right)=0$ 且 $\phi$ 在开区间 $\left(0,\eta \right)$ 上连续可微；

2) 对所有的 $s\in \left(0,\eta \right)$， ${\phi }^{\prime }\left(s\right)>0$，以及点 $\bar{x}$ 的邻域U使得对所有 $x\in U\cap \left[f\left(\bar{x}\right)<f<f\left(\bar{x}\right)+\eta \right]$，都有下述不等式成立

${\phi }^{\prime }\left(f\left(x\right)-f\left(\bar{x}\right)\right)\text{dist}\left(0,\partial f\left(x\right)\right)\ge \text{1}$，

则称函数f在点 $\bar{x}$ 处具有KL性质。若f在集合 $\text{dom}\partial f$ 中的每点都具有KL性质，则称f是KL函数。

定义2 [10] (Lipschitz连续)设F为从集合 $D\subset {ℝ}^n$ 到 ${ℝ}^m$ 上的单值映射。设 $X\subset D$。F在X上是Lipschitz连续的，若存在 $\kappa \in {ℝ}_{+}=\left[0,+\infty \right)$，满足

$\Vert F\left(x^{\prime }\right)-F\left(x\right)\Vert \le \kappa \Vert x^{\prime }-x\Vert ,\forall x,x^{\prime }\in X$。

其中 $\kappa$ 称为F在X上的Lipschitz常数。

定义3 [10] (次微分)函数 $f\left(x\right)$ 在x处的所有次梯度的集合称为 $f\left(x\right)$ 在x处的次微分，即

$\partial f\left(x\right)=\left\{x^{\ast }\in X^{\ast }:f\left(y\right)-f\left(x\right)\ge \langle x^{\ast },y-x\rangle ,\forall y\in X\right\}$。

$\text{dom}\partial F\left(x\right)=\left\{x|\partial F\left(x\right)\ne \varnothing \right\}$。

定义4 [11] 设存在 $f_0\in R$，S是一非空子集，满足 $f\left(x\right)=f_0$， $\forall x\in S$，令 $\gamma$ 是一正的常数。称 $\gamma$ 阶增长条件在S上成立，若存在常数 $c>0$，存在S的邻域V，满足对所有的 $x\in {ℝ}^n\cap V$，下述不等式成立：

$f\left(x\right)\ge f_0+c{\left[\text{dist}\left(x,S\right)\right]}^{\gamma }$。

尤其，若 $\gamma =1$，称一阶增长条件成立，若 $\gamma =2$，称第二阶(或二阶)增长条件成立。

定义5 [11] (凸函数)设C是一凸集合， $f:C\to \left(-\infty ,+\infty \right]$ 是一增广实值函数。对任意 $x\in C$， $y\in C$，有

$f\left(\left(1-t\right)x+ty\right)\le \left(1-t\right)f\left(x\right)+tf\left(y\right)$， $0<t<1$。

则函数f是C上的凸函数。

引理1 对任意给定的 $x\in {ℝ}^n$，

$\partial {\Vert \cdot \Vert }_1\left(x\right)=\left\{\mu \in R^n|{\mu }_i=\{\begin{array}{l}1x_i>0\hfill \\ -1x_i<0\hfill \\ \left[-1,1\right]x_i=0\hfill \end{array},i=1,2,\cdots ,n\right\}$。

注记1 根据文献 [12] 中的引理2.1，一个正常函数在所有非稳定点处具有KL性质。因此为了证明它是KL函数，只需证明函数在任意稳定点处是否具有KL性质。

注记2 若 $0\in \partial f\left(\bar{x}\right)$，则称 $\bar{x}$ 是函数f的稳定点，记 $\text{crit}f$ 为f的稳定点集。

3. 主要结果及其应用

考虑如下问题模型

$\underset{x\in R^n}{\min }\left\{f\left(x\right):=\frac{\lambda }{2}{\Vert Ax-b\Vert }^2+{\Vert x\Vert }_1\right\}$， (3)

其中， $A\in {ℝ}^{m\times n}$ ( $m<n$ )， $x\in {ℝ}^n$， $b\in {ℝ}^m$， $\lambda >1$ 为参数， $\Vert x\Vert =\sqrt{x_1^2+x_2^2+\cdots +x_n^2}$，

${\Vert x\Vert }_1=\left|x_1\right|+\left|x_2\right|+\cdots +\left|x_n\right|$。

记 $f_1\left(x\right):=\frac{\lambda }{2}{\Vert Ax-b\Vert }^2$， $f_2\left(x\right):={\Vert x\Vert }_1$，则 $f\left(x\right)=f_1\left(x\right)+f_2\left(x\right)$。

引理2 [13] 对于任意的 $x\in {ℝ}^n$，给定 $p>0$，则p范数，即 ${\Vert x\Vert }_p={\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{\Vert x_i\Vert }^p}\right)}^{\frac{1}{p}}$，具有KL性质。

由引理2知， $f_2\left(x\right)$ 具有KL性质。

引理3 [14] 假设 $f_1$ 在 $\text{dom}{f}_2$ 上具有 $L>0$ 的Lipschitz连续梯度，即

$\Vert \nabla f_1\left(x\right)-\nabla f_1\left(y\right)\Vert \le L\Vert x-y\Vert \forall x,y\in \text{dom}{f}_2$。

且 $f\left(x\right)$ 是下有界的。则

$\partial f\left(x\right)=\left\{\nabla f_1\left(x\right)\right\}+\partial f_2\left(x\right)\forall x\in \text{dom}f$。

定理1 假设 $f_1\left(x\right)$ 在 $\text{dom}f$ 上局部Lipschitz连续，对 $\forall \bar{x}\in \text{dom}\partial f$，若 $f_1\left(x\right)$ 在 $\bar{x}$ 点处满足二阶增长条件，即

$f_1\left(x\right)\ge f_1\left(\bar{x}\right)+c{\Vert x-\bar{x}\Vert }^2$ $c>0$，

则 $f\left(x\right)$ 为KL函数。

证明：由 $f_1\left(x\right)=\frac{\lambda }{2}{\Vert Ax-b\Vert }^2$， $\forall x\in {ℝ}^n$，可知 $\nabla f_1\left(x\right)=\lambda *A^{\text{T}}\left(Ax-b\right)$ 和 ${\nabla }^2{f}_1\left(x\right)=A^{\text{T}}A$。因此 $f_1\left(x\right)$ 是凸的，且在 $\bar{x}$ 点满足二阶增长条件。由次微分定义，有下式成立

$f_1\left(\bar{x}\right)-f_1\left(x\right)\ge \lambda \langle A^{\text{T}}\left(Ax-b\right),\bar{x}-x\rangle$ $\forall x\in {ℝ}^n$。

即

$f_1\left(x\right)-f_1\left(\bar{x}\right)\le \lambda \langle A^{\text{T}}\left(Ax-b\right),x-\bar{x}\rangle$ $\forall x\in {ℝ}^n$。

因此有

$f_1\left(x\right)-f_1\left(\bar{x}\right)\le \lambda \Vert A^{\text{T}}\left(Ax-b\right)\Vert \cdot \Vert x-\bar{x}\Vert$ $\forall x\in {ℝ}^n$。 (4)

由于 $f_1\left(x\right)$ 在 $\bar{x}$ 点处二阶增长条件，可得

$f_1\left(x\right)-f_1\left(\bar{x}\right)\ge c{\Vert x-\bar{x}\Vert }^2$ $\forall x\in {ℝ}^n$。 (5)

将(4)和(5)结合，可得

$c{\Vert x-\bar{x}\Vert }^2\le \lambda \Vert A^{\text{T}}\left(Ax-b\right)\Vert \cdot \Vert x-\bar{x}\Vert$ $\forall x\in {ℝ}^n$。

即

$\sqrt{c}\le \frac{\sqrt{\lambda }\sqrt{\Vert A^{\text{T}}\left(Ax-b\right)\Vert }}{\sqrt{\Vert x-\bar{x}\Vert }}$ $\forall x\in {ℝ}^n$。 (6)

考虑 $\phi \left(s\right)=\frac{2}{\sqrt{c}}\sqrt{s}$， $\forall s\in \left(0,{\eta }_1\right)$，其中 ${\eta }_1\in \left(0,+\infty \right]$，有

${\phi }^{\prime }\left(s\right)=\frac{1}{\sqrt{cs}}$， ${\phi }^{″}\left(s\right)=-\frac{1}{2\sqrt{c{s}^3}}$，

则 $\phi \left(s\right)$ 在 $\left[0,{\eta }_1\right)$ 上是凹函数。所以对于 ${\delta }_1>0$， $\forall x\in B\left(\bar{x},{\delta }_1\right)\cap \left[f_1\left(\bar{x}\right)<f_1\left(x\right)<f_1\left(\bar{x}\right)+{\eta }_1\right]$，有

${\phi }^{\prime }\left(f_1\left(x\right)-f_1\left(\bar{x}\right)\right)=\frac{1}{\sqrt{c\left(f_1\left(x\right)-f_1\left(\bar{x}\right)\right)}}$。

将(4)式与上式结合，可得到下式

${\phi }^{\prime }\left(f_1\left(x\right)-f_1\left(\bar{x}\right)\right)\ge \frac{1}{\sqrt{c}\sqrt{\lambda }\sqrt{\Vert A^{\text{T}}\left(Ax-b\right)\Vert \cdot \Vert x-\bar{x}\Vert }}$。(7)

由距离函数的定义，有

$\text{dist}\left(0,\partial f_1\left(x\right)\right)=\sqrt{\lambda }\Vert A^{\text{T}}\left(Ax-b\right)\Vert$。 (8)

再将(7)式与(8)式结合，得

${\phi }^{\prime }\left(f_1\left(x\right)-f_1\left(\bar{x}\right)\right)\text{dist}\left(0,\partial f_1\left(x\right)\right)\ge \frac{1}{\sqrt{c}\sqrt{\lambda }\sqrt{\Vert A^{\text{T}}\left(Ax-b\right)\Vert \cdot \Vert x-\bar{x}\Vert }}\sqrt{\lambda }\Vert A^{\text{T}}\left(Ax-b\right)\Vert$。(9)

将(6)式带入(9)式，就可以得到

${\phi }^{\prime }\left(f_1\left(x\right)-f_1\left(\bar{x}\right)\right)\text{dist}\left(0,\partial f_1\left(x\right)\right)\ge 1$。

故 $f_1\left(x\right)$ 在 $\bar{x}$ 点处满足KL性质。由 $\bar{x}$ 的任意性，则 $f_1\left(x\right)$ 在集合 $\text{dom}\partial f$ 中的每点都具有KL性质，即 $f_1\left(x\right)$ 是KL函数。

由于函数 $f_1\left(x\right)$ 在 $\bar{x}$ 处具有连续性，因此对 $\forall {\eta }_2\in \left(0,1\right)$， $\exists {\delta }_2>0$ 有下式成立

$\left|f_1\left(x\right)-f_1\left(\bar{x}\right)\right|\le {\eta }_2\forall x\in B\left(\bar{x},{\delta }_2\right)$。

由 $f_1\left(x\right)$ 是KL函数。 结合定义1，对 $\forall x\in B\left(\bar{x},{\delta }_1\right)\cap \left[f_1\left(\bar{x}\right)<f_1\left(x\right)<f_1\left(\bar{x}\right)+{\eta }_1\right]$ 有下式成立：

$\text{dist}\left(0,\partial f_1\left(x\right)\right)\ge \sqrt{c}\sqrt{f_1\left(x\right)-f_1\left(\bar{x}\right)}$。 (10)

令 $\delta =\min \left\{{\delta }_1,{\delta }_2\right\}$ 和 $\eta =\min \left\{{\eta }_1,{\eta }_2\right\}$。对 $\forall x\in B\left(\bar{x},\delta \right)\cap \left[f\left(\bar{x}\right)<f\left(x\right)<f\left(\bar{x}\right)+\eta \right]$，有

$\underset{z\in \partial F\left(x\right)}{\min }\Vert z\Vert =\text{dist}\left(0,\partial f\left(x\right)\right)$。 (11)

由 $\partial f\left(x\right)$ 是闭集，则 $\exists z^{\ast }\in \partial f\left(x\right)$，满足 $\Vert z^{\ast }\Vert =\text{dist}\left(0,\partial f\left(x\right)\right)$。由于 $f_1$ 在 $\bar{x}$ 处具有局部Lipschitz连续性，结合引理3，有 $\partial f\left(x\right)=\partial f_1\left(x\right)+\partial {\Vert \cdot \Vert }_1\left(x\right)$。结合引理1中的 $\partial {\Vert \cdot \Vert }_1\left(x\right)$ 的表达式以及式(11)，有

${\Vert z^{\ast }\Vert }^2={\text{dist}}^2\left(0,\partial f_1\left(x\right)+\partial {\Vert \cdot \Vert }_1\left(x\right)\right)\ge {\lambda }^2{\Vert A^{\text{T}}\left(Ax-b\right)\Vert }^2$。 (12)

通过式(11)和式(12)，有下式：

$\text{dist}{\left(0,\partial f\left(x\right)\right)}^2={\Vert z^{\ast }\Vert }^2\ge {\lambda }^2{\Vert A^{\text{T}}\left(Ax-b\right)\Vert }^2=\text{dist}{\left(0,\partial f_1\left(x\right)\right)}^2$。 (13)

将 $f_1\left(\bar{x}\right)<f_1\left(x\right)$ 与 $f\left(x\right)<f\left(\bar{x}\right)+\eta$ 结合，可以得到 ${\Vert x\Vert }_1\le {\Vert \bar{x}\Vert }_1$。由式(10)和(13)，有

$\text{dist}{\left(0,\partial f\left(x\right)\right)}^2\ge \text{dist}{\left(0,\partial f_1\left(x\right)\right)}^2\ge c\left(f_1\left(x\right)-f_1\left(\bar{x}\right)\right)\ge c\left(f\left(x\right)-f\left(\bar{x}\right)\right)$。

上述不等式说明了 $f\left(x\right)$ 在 $\bar{x}$ 处具有KL性质。由于 $\bar{x}$ 在 $\text{dom}\partial f$ 中的任意性，故 $f\left(x\right)$ 是KL函数。

4. 非单调线搜索收敛算法

本节将采用非单调线搜索算法求步长，采用BB [15] 步长作为每次迭代的初始步长，经过有限步的线搜索，就可以找到符合收敛条件的步长，该算法充分说明了该问题模型满足KL性质，基于KL性质可以分析算法的收敛性。

令 $g^k\in \partial f\left(x^k\right)$，Hessian矩阵 $H^k\in {\partial }^{2}f\left(x^k\right)$，其中 $k\in \text{N}$，则牛顿迭代为

$x^{k+1}=x^k-{\left(H^k\right)}^{-1}{g}^k$。 (14)

用BB法可以得到Hessian矩阵 $H^k\approx {\alpha }_k^{-1}I$，其中 ${\alpha }_k>0$，I为 $n\times n$ 单位矩阵。将(14)式中的 $H^k$ 替换为 ${\alpha }_k^{-1}I$，得到

$x^{k+1}=x^k-{\alpha }_k{g}^k$。 (15)

设 $\Delta g^k=g^k-g^{k-1}$， $\Delta x^k=x^k-x^{k-1}$，则

$g^k-g^{k-1}=H^k\left(x^k-x^{k-1}\right)$。

即

$\Delta g^k=H^k\Delta x^k$。

将上式中的 $H^k$ 替换为 ${\alpha }_k^{-1}I$，得到 $\Delta g^k={\alpha }_k^{-1}\Delta x^k$，所以 ${\alpha }_k{\left(\Delta x^k\right)}^{\text{T}}\Delta g^k={\left(\Delta x^k\right)}^{\text{T}}\Delta x^k$，即 ${\alpha }_k=\frac{{\Vert \Delta x^k\Vert }^2}{\langle \Delta x^k,\Delta g^k\rangle }$。令 $B^k={\alpha }_{k}I$，迭代格式(15)也可以写为

$x^{k+1}=x^k-B^k{g}^k$。 (16)

BB法选取的步长，满足下式：

${\alpha }_k=\underset{\alpha }{\arg \min }{\Vert \alpha \Delta g^k-\Delta x^k\Vert }_2^2$， ${\alpha }_k=\underset{\alpha }{\arg \min }{\Vert \Delta g^k-{\alpha }^{-1}\Delta x^k\Vert }_2^2$。

即步长为

${\alpha }_k^{BB1}=\frac{{\Vert \Delta x^k\Vert }^2}{\langle \Delta x^k,\Delta g^k\rangle }$， ${\alpha }_k^{BB2}=\frac{\langle \Delta x^k,\Delta g^k\rangle }{{\Vert \Delta g^k\Vert }^2}$， (17)

则 ${\alpha }_k$ 为第k次迭代的初始步长。设L是 $A^{\text{T}}A$ 的特征值中最大的一个数，初始步长 ${\alpha }_0=\frac{1}{L}$，为了保证全局收敛性，非单调步长准则，如下式

$f\left(x^k-{\alpha }_k{g}^k\right)\le C^k-c_1{\alpha }_k{\Vert g^k\Vert }^2$。 (18)

其中 $C_k$ 满足 $C_0=f\left(x^0\right)$， $C_{k+1}=\frac{1}{Q_{k+1}}\left(\tau Q_k{C}_k+f\left(x^{k+1}\right)\right)$， $Q_0=1$， $Q_{k+1}=\tau Q_k+1$， $c_1,\tau \in \left(0,1\right)$。

算法的具体步骤如下：

输入： $A,b,x^0,\tau \in \left(0,1\right),c_1\in \left(0,1\right),\epsilon \in \left(0,1\right),Q_0=1,\lambda =100,k=0,{\alpha }_0$ ；

输出： $x=x^{k+1}$

步骤1：初始化 $g^0=\lambda \ast A^{\text{T}}\left(A{x}^0-b\right)+sign\left(x^0\right)$， $C_0=f\left(x^0\right)$ ；

步骤2：当 $\Vert g^k\Vert >\epsilon$ 时，向下进行；否则停止计算；

步骤3：当 $f\left(x^k-{\alpha }_k{g}^k\right)>C^k-c_1{\alpha }_k{\Vert g^k\Vert }^2$ 时， ${\alpha }_k=0.6{\alpha }_k$ ；否则向下进行；

步骤4：迭代 $x^{k+1}=x^k-{\alpha }_k{g}^k$ ；

步骤5：通过(17)式获取步长 ${\alpha }_{k+1}$，且满足 ${\alpha }_{k+1}\in \left[{10}^{-20},{10}^{20}\right]$，再计算 $C_{k+1}$， $Q_{k+1}$ ；令 $k=k+1$，返回步骤2。

变量 $C_k$ 实际上为本次搜索准则的参照函数值，即充分下降性质的起始准则； $C_{k+1}$ 是函数值 $f\left(x^{k+1}\right)$ 和 $C_k$ 的凸组合，并不是仅仅依赖于 $f\left(x^{k+1}\right)$，而凸组合的两个系数由参数 $\tau$ 决定。这就说明 $C_k$ 包含之前算过的所有目标函数值。综上所述，本文提出的算法是可行有效的。

5. 实验结果分析及讨论

通过MATLAB实验来证明该算法在重构信号方面的优势，实验运行平台的配置如下：Intel(R)Core (TM)i5-10400F CPU @2.90 GHz；内存16.00 GB。在不同的MATLAB版本测试下，结果不会发生较大变化。本文实验在MATLAB R2020b中进行。

实验取 $n=2048$， $m=512$， $a=64$，a表示原始信号中非零元的个数。其中非零元的位置均是随机选取的，A是与高斯矩阵独立同分布的随机矩阵 [16]， $b=A{x}^0+\omega$，其中 $\omega \in {ℝ}^m$， $\omega$ 是分布为 $N\left(0,{\sigma }^{2}I\right)$ 的高斯噪声，取 ${\sigma }^2={10}^{-3}$， $\epsilon ={10}^{-4}$， ${\alpha }_k=\min \left\{\max \left\{{\alpha }_k,{10}^{-20}\right\},{10}^{20}\right\}$。在线搜索过程中，选取初始步长 ${\alpha }_0=0.8$， $c_1={10}^{-6}$， $\tau =0.85$。相对误差定义为

$\text{RelErr}=\frac{{\Vert \hat{x}-\bar{x}\Vert }_2}{{\Vert \bar{x}\Vert }_2}$，

其中 $\hat{x}$ 表示重构信号， $\bar{x}$ 表示原始信号。相对误差用来测量重构信号的质量。当相邻两点的相对误差充分小，即

$\frac{{\Vert x_k-x_{k-1}\Vert }_2}{{\Vert x_{k-1}\Vert }_2}<\epsilon$，

时，则停止迭代。原始信号，观测向量及重构信号如图1所示。

比较图1中的(a)和(c)可以分析出来，所有的蓝点均被红点包围，这说明原始信号几乎被精确重构。上述实验表明，该算法效果良好，相对误差较小，为恢复大的稀疏信号提供了一种有效的方法。

本文在接下来的实验中，采用了4种不同的信号，对不同的算法进行比较分析。取上述实验中的初始参数，对NBBL1n和NBBL1这2种算法进行了对比和分析。在初始和终止条件相同的情况下，从函数值下降的角度分析，无论针对那种信号，NBBL1n算法下降总是最快的，迭代次数也最少，为进一步说明结果，表1和表2给出了详细的对比数据。由于设下随机种子，所以每次获取的信号是不变的。所以误差很小。

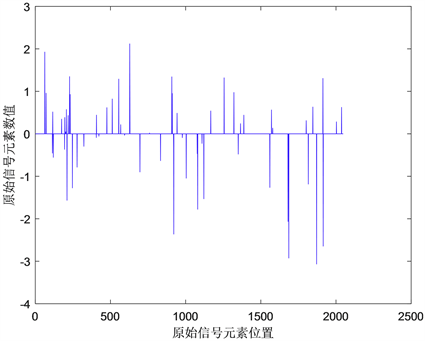(a) 原始信号 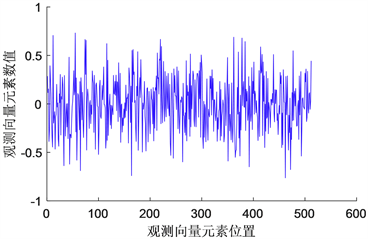(b) 观测向量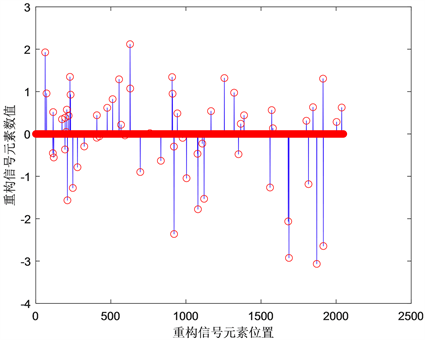(c) NBBL1n (RelErr = 1.38%)

Figure 1. The effectiveness of the NBBL1n algorithm

图1. NBBL1n算法的有效性

Table 1. Comparison of the number of iterations of the time required by the algorithm for different sparsity degrees

表1. 对于不同稀疏度，算法所需要的时间的迭代次数对比

表1中详细的列出了4种不同信号的运行时间和迭代次数。从表中可以分析出，随着信号规模的不断增大，运行算法所需要的时间也明显增加，但是通过对比，新版本算法的运行总用时较少，迭代次数也比较少。

Table 2. When c taken 0.4, each step iterative gradient norm vs $\sqrt{c\left(f\left(x^k\right)-f\left(\bar{x}\right)\right)}$

表2. 取 $c=0.4$ 时，每步迭代梯度范数与 $\sqrt{c\left(f\left(x^k\right)-f\left(\bar{x}\right)\right)}$ 的对比

表2取稀疏度为0.04，为了表示一般性，45次迭代做了对比分析，充分说明了新算法满足KL不等式。再对比表1，可以得到，满足KL性质的非单调线搜索算法，无论稀疏度如何，算法均可以达到最优。

6. 结束语

本文将结合非单调线搜索算法和BB步长，在满足KL性质的基础上，将算法应用于压缩感知问题模型，数值实验结果表明，当原始信号的稀疏度不同时，该方法是可行有效的。本文的方法无论是从运行时间还是迭代次数上均有不同程度的改进。但将本文的非单调线搜索应用到其他问题中是否有较好的效果，仍需要进一步研究。

基金项目

辽宁省教育厅科学研究一般项目(LJ2019005)。

NOTES

^*通讯作者。