Delta算子系统的状态量化H∞控制

H∞ Control for Delta Operator Systems with State Quantization

摘要: 本文主要研究Delta算子系统的状态量化H∞控制问题，首先设计状态反馈控制器，使得Delta算子系统是渐进稳定，且满足一定的H∞性能指标。此外，考虑应用动态量化器，使得Delta算子系统在动态量化器下也能够满足相同的H∞性能指标。基于Lyapunov函数，利用线性矩阵不等式对目标进行设计，最后，通过数值算例验证了所给方法的可行性和有效性。

Abstract: This paper mainly studies the H∞ control for Delta operator systems with state quantization. Firstly, by designing state feedback controller, the Delta operator systems are asymptotically stable and satisfy the H∞ performance index. In addition, considering the dynamic quantizer, the delta operator systems can satisfy the same performance index under it. Based on a Lyapunov function, the target is designed by using linear matrix inequality. Finally, a numerical example is given to verify the feasibility and effectiveness of the design method.

1. 引言

Delta算子是用来描述离散系统的一种方法 [1]，相较于传统前向移位算子来说，其不仅可以拥有前向移位算子的全部优点，且在高速采样的情况下，Delta算子离散化方法可以避免传统前向移位算子离散化方法引起的数值不稳定问题。当采样周期无限趋于零时，Delta算子公式化模型趋近相应的离散化前的连续时间模型，故连续时间系统的设计方法可以直接应用于离散时间系统，可以获得更好的控制结果。近年来，国内外学者对于Delta算子系统的研究逐渐深入，例如，Zhang等人 [2] 研究了Delta算子系统的故障检测问题。肖民卿 [3] 研究了一系列Delta算子系统的控制问题。向峥嵘等人 [4] 研究了Delta算子描述的区间系统的鲁棒性能稳定分析与综合设计问题。胡号 [5] 研究了几类Delta算子切换系统的容错控制问题。

可靠鲁棒 ${\text{H}}_{\infty }$ 控制是存在外界扰动或不确定系统模型下，设计控制器，使得外界扰动与系统模型的不确定性对系统输出的影响尽可能地小。对其的研究也受到了国内外学者的广泛关注，例如，Gao等人 [6] 对具有导数不确定性的广义Delta算子系统的鲁棒 ${\text{H}}_{\infty }$ 控制问题进行了研究。Chang等人 [7] 进一步研究了离散时间系统输出反馈 ${\text{H}}_{\infty }$ 的控制问题，提出了输出反馈 ${\text{H}}_{\infty }$ 控制器设计的新条件。Wang等人 [8] 研究了一类具有状态量化的离散时间系统的 ${\text{H}}_{\infty }$ 控制问题。

由于传感器精度以及带宽限制，数据在传输之前需要进行量化。在量化过程中，量化误差会影响系统的稳定性以及其他性能。近年来，学者们对量化控制系统方面进行了大量的研究 [9] [10]，表明减少量化误差对网络系统有一定的正向影响，并采取了多种量化方法来解决量化误差对系统产生的影响。在 [11] 中，Fu等人研究了线性系统的量化反馈设计问题，考虑了静态量化器的情况。除静态量化器外，动态量化器也经常用于控制系统，其可以根据实际情况通过调整动态参数来调整系统性能。动态量化器的优点是通过调整动态参数可以获得不同的量化范围和量化误差。 [12] 提出了一种新的量化输出控制策略，给出了输出反馈控制器和动态量化器参数的相应设计方法。事实上，动态量化器由静态量化器和动态参数组成。因此，在动态量化器的研究中，对于参数的调整十分重要。之前的研究方法大多将动态参数的设计依赖于系统矩阵，但实施起来具有一定的难度。因此一些学者提出了新的动态量化策略和新的动态参数调整规则，这对于动态量化器的实际应用具有重要意义，会提高动态量化器的适用性。除了以上问题，动态量化器还存在一些问题没有解决。因此，越来越多的学者选择对其进行研究。

本文在第2节中对所研究Delta算子系统的状态量化 ${\text{H}}_{\infty }$ 控制问题进行了描述。第3节中根据Lyapunov稳定性理论，利用线性矩阵不等式给出了Delta算子系统渐进稳定的条件，给出了具有一定的 ${\text{H}}_{\infty }$ 性能的状态反馈控制器的设计方法，并考虑动态量化器，使得Delta算子系统在动态量化器下可以满足同样的 ${\text{H}}_{\infty }$ 性能指标。第4节中利用所给数值算例说明了所给方法的有效性和实用性。

符号说明： $R$ 表示实数域， $R^n$ 代表n维欧几里得空间， $R^{n\times m}$ 表示维数为 $n\times m$ 的所有实矩阵的集合。 $A^{\text{T}}$ 表示矩阵 $A$ 的转置， $A^{-1}$ 表示矩阵 $A$ 的逆。 $I$ 表示适当阶数的单位矩阵， $0$ 表示适当阶数的零矩阵。对称矩阵中的“*”表示矩阵相应的对称分块。 $S>0\left(S<0\right)$ 表示矩阵 $S$ 是对称正(负)定矩阵， $S\ge 0\left(S\le 0\right)$ 表示矩阵 $S$ 是对称半正(负)定矩阵，对于两个对称矩阵 $A$， $B$， $A<B\left(A\le B\right)$ 表示矩阵 $B-A$ 是正定(半正定)。 $|\cdot |$ 表示向量的欧几里得范数， $\Vert \cdot \Vert$ 表示矩阵的谱范数。

为解决下文中的问题，提前给出以下两个引理。

引理1 [13] 对给定矩阵 $S=\left[\begin{array}{cc}{S}_{11}& S_{12}\\ S_{21}& S_{22}\end{array}\right]$，其中 $S_{11}$ 是 $r\times r$ 的，以下三个条件等价：

1) $S<0$ ；

2) $S_{11}<0$， $S_{22}-S_{21}{S}_{11}^{-1}{S}_{12}<0$ ；

3) $S_{22}<0$， $S_{11}-S_{12}{S}_{22}^{-1}{S}_{21}<0$。

引理2 对于具有适当维数的矩阵 $F$， $T$， $S$ 和 $U$，并给定标量 $\xi$，则以下两个条件等价：

1) $T+S^{\text{T}}{F}^{\text{T}}+FS<0$ ；

2) $\left[\begin{array}{cc}T& *\\ \xi F^{\text{T}}+US& -\xi U-\xi U^{\text{T}}\end{array}\right]<0$。

2. 问题描述

Delta算子的定义为：

$\delta =\frac{q-1}{h}$

其中 $q$ 为前向移位算子，即 $qx\left(k\right)=x\left(k+1\right)$， $h$ 为系统采样周期。

考虑以下具有扰动的Delta算子系统：

$\{\begin{array}{l}\delta x\left(k\right)=Ax\left(k\right)+Bu\left(k\right)+E\omega \left(k\right)\\ y\left(k\right)=Cx\left(k\right)\end{array}$ (1)

其中 $x\left(k\right)\in R^n$ 为系统状态向量， $u\left(k\right)\in R^m$ 为输入向量， $\omega \left(k\right)\in R^s$ 为外部扰动输入， $y\left(k\right)\in R^l$ 为系统测量输出。 $A\in R^{n\times n}$， $B\in R^{n\times m}$， $C\in R^{l\times n}$， $E\in R^{n\times s}$ 为已知常数矩阵。

采用如下状态反馈控制器：

$u\left(k\right)=Kx\left(k\right)$ (2)

其中 $K$ 为待确定的控制器增益矩阵。

将控制器(2)代入系统(1)可得如下闭环系统：

$\{\begin{array}{l}\delta x\left(k\right)=\left(A+BK\right)x\left(k\right)+E\omega \left(k\right)\\ y\left(k\right)=Cx\left(k\right)\end{array}$ (3)

本文的目的是设计状态反馈控制器(2)，使得Delta算子闭环系统(3)是渐进稳定的，且符合 $H_{\infty }$ 性能，系统应该满足以下条件：

1) 当 $\omega \left(k\right)=0$ 时，闭环系统(3)是渐近稳定的；

2) 当 $\omega \left(k\right)\ne 0$ 时，对于标量 $\gamma >0$，系统测量输出和外部扰动输入应满足 ${\displaystyle \underset{k=0}{\overset{\infty }{\sum }}{\Vert y\left(k\right)\Vert }^2}<{\gamma }^2{\displaystyle \underset{k=0}{\overset{\infty }{\sum }}{\Vert \omega \left(k\right)\Vert }^2}$。

3. 主要结论

在本节中，为了解决Delta算子系统的状态量化 $H_{\infty }$ 控制问题，首先讨论Delta算子闭环系统(3)在 $H_{\infty }$ 性能指标下的渐进稳定性，利用参数相关的Lyapunov函数和线性矩阵不等式方法，得到如下定理。

定理1 对于给定标量 $\gamma >0$ 和给定矩阵 $Q$，若存在矩阵 $P=P^{\text{T}}>0$， $G$ 、 $R$ 、 $U>0$，使得以下线性矩阵不等式成立，

$\left[\begin{array}{cccc}{\hat{\Omega }}_2& *& *& *\\ {\hat{\Omega }}_1& -P& *& *\\ {\Omega }_3& 0& -I& *\\ {\Omega }_4& \xi {\left(hPB-QU\right)}^{\text{T}}& 0& {\Omega }_5\end{array}\right]<0$ (4)

其中，

${\hat{\Omega }}_2=\left[\begin{array}{cc}-P+R_{11}& *\\ R_{21}& -{\gamma }^{2}I+R_{22}+E^{\text{T}}PE\end{array}\right]$

${\hat{\Omega }}_{\text{1}}=\left[\begin{array}{cc}P+hPA+QG& hPE\end{array}\right]$， ${\Omega }_3=\left[\begin{array}{cc}C& 0\end{array}\right]$， ${\Omega }_4=\left[\begin{array}{cc}G& 0\end{array}\right]$， ${\Omega }_5=-\xi U-\xi U^{\text{T}}$

则可得Delta算子闭环系统(3)在 $H_{\infty }$ 性能指标下渐进稳定。

证明 考虑Lyapunov函数

$V\left(x\left(k\right)\right)={\text{x}}^{\text{T}}\left(k\right)\text{Px}(\; k\; )$

因

$\begin{array}{l}\text{x}\left(k+1\right)=h\delta \text{x}\left(k\right)+\text{x}\left(k\right)\\ =h\left[\left(\text{A}+\text{BK}\right)\text{x}\left(k\right)+\text{Eω}\left(k\right)\right]+\text{x}\left(k\right)\\ =\left[\text{I}+h\left(\text{A}+\text{BK}\right)\right]\text{x}\left(k\right)+h\text{Eω}(\; k\; )\end{array}$

故可得，

$\begin{array}{l}\Theta ={\text{y}}^{\text{T}}\left(k\right)\text{y}\left(k\right)-{\gamma }^2{\text{ω}}^{\text{T}}\left(k\right)\text{ω}\left(k\right)+{\text{ω}}^{\text{T}}\left(k\right){\text{E}}^{\text{T}}\text{PEω}\left(k\right)+\Delta V\left(\text{x}\left(k\right)\right)\\ ={\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]}^{\text{T}}\left({\left[\begin{array}{cc}\text{C}& 0\end{array}\right]}^{\text{T}}\left[\begin{array}{cc}\text{C}& 0\end{array}\right]-\left[\begin{array}{cc}\text{P}& 0\\ 0& {\gamma }^2\text{I}-{\text{E}}^{\text{T}}\text{PE}\end{array}\right]+{\left[\begin{array}{cc}\text{I}+h\left(\text{A}+\text{BK}\right)& h\text{E}\end{array}\right]}^{\text{T}}\text{P}\left[\begin{array}{cc}\text{I}+h\left(\text{A}+\text{BK}\right)& h\text{E}\end{array}\right]\right)\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]\\ ={\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]}^{\text{T}}\left({\left[\begin{array}{cc}\text{I}+h\left(\text{A}+\text{BK}\right)& h\text{E}\end{array}\right]}^{\text{T}}\text{P}\left[\begin{array}{cc}\text{I}+h\left(\text{A}+\text{BK}\right)& h\text{E}\end{array}\right]+\left[\begin{array}{cc}-\text{P}+{\text{C}}^{\text{T}}\text{C}& 0\\ 0& -{\gamma }^2\text{I+}{\text{E}}^{\text{T}}\text{PE}\end{array}\right]\right)\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]\\ ={\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]}^{\text{T}}\left({\Omega }_1+{\Omega }_2\right)\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]\end{array}$

即其中

${\Omega }_1={\left[\begin{array}{cc}\text{I}+h\left(\text{A}+\text{BK}\right)& h\text{E}\end{array}\right]}^{\text{T}}\text{P}\left[\begin{array}{cc}\text{I}+h\left(\text{A}+\text{BK}\right)& h\text{E}\end{array}\right]$

${\Omega }_2=\left[\begin{array}{cc}-\text{P}+{\text{C}}^{\text{T}}\text{C}& 0\\ 0& -{\gamma }^2\text{I}+{\text{E}}^{\text{T}}\text{PE}\end{array}\right]$。

因此，若 $\Theta <0$，可得，

${\text{y}}^{\text{T}}\left(k\right)\text{y}\left(k\right)-{\gamma }^2{\text{ω}}^{\text{T}}\left(k\right)\text{ω}\left(k\right)+\Delta V\left(\text{x}\left(k\right)\right)<-{\text{ω}}^{\text{T}}\left(k\right){\text{E}}^{\text{T}}\text{PEω}\left(k\right)<0$

即证得Delta算子闭环系统(3)在 $H_{\infty }$ 性能指标下渐进稳定，下面证明 $\Theta <0$。

设 $\text{R}=\left[\begin{array}{cc}{\text{R}}_{11}& *\\ {\text{R}}_{21}& {\text{R}}_{22}\end{array}\right]>0$，若能证明 $\Theta <-\text{R}$，则 $\Theta <0$ 成立，即证明 $\Theta +\text{R}<0$。

下面证明 ${\Omega }_1+{\bar{\Omega }}_2<0$，其中

${\bar{\Omega }}_2={\Omega }_2+\text{R}=\left[\begin{array}{cc}-\text{P}+{\text{C}}^{\text{T}}\text{C}+{\text{R}}_{11}& *\\ {\text{R}}_{21}& -{\gamma }^2\text{I}+{\text{E}}^{\text{T}}\text{PE}+{\text{R}}_{22}\end{array}\right]$ (5)

根据引理1，(5)式等价于

$\left[\begin{array}{cc}{\bar{\Omega }}_2& *\\ {\bar{\Omega }}_1& -{\text{P}}^{-1}\end{array}\right]<0$ (6)

其中 ${\bar{\Omega }}_1=\left[\begin{array}{cc}\text{I}+h\left(\text{A}+\text{BK}\right)& h\text{E}\end{array}\right]$，将 $\text{diag}\left\{\text{I},\text{I},\text{P}\right\}$ 分别左乘、右乘于(6)式的两边，得到

$\left[\begin{array}{cc}{\bar{\Omega }}_2& *\\ {\tilde{\Omega }}_1& -\text{P}\end{array}\right]<0$ (7)

其中 ${\tilde{\Omega }}_1=\left[\begin{array}{cc}\text{P}+h\left(\text{PA}+\text{PBK}\right)& h\text{PE}\end{array}\right]$，根据引理1，(7)式等价于

$\left[\begin{array}{ccc}{\hat{\Omega }}_{\text{2}}& *& *\\ {\tilde{\Omega }}_1& -\text{P}& *\\ {\Omega }_{\text{3}}& 0& -\text{I}\end{array}\right]<0$ (8)

设 $\text{K}={\text{U}}^{-1}\text{G}$，则(8)式可以写为

$\left[\begin{array}{ccc}{\hat{\Omega }}_{\text{2}}& *& *\\ {\hat{\Omega }}_{\text{1}}& -\text{P}& *\\ {\Omega }_{\text{3}}& 0& -\text{I}\end{array}\right]+{\left(\text{M}{\text{U}}^{-1}\text{GN}\right)}^{\text{T}}+\text{M}{\text{U}}^{-1}\text{GN}<0$ (9)

其中 $M={\left[\begin{array}{cccc}0& 0& {\left(hPB-QU\right)}^{\text{T}}& 0\end{array}\right]}^{\text{T}}$， $\text{N}=\left[\begin{array}{cccc}\text{I}& 0& 0& 0\end{array}\right]$，设 $\text{F}=\text{M}$， $\text{S}={\text{U}}^{-1}\text{GN}$，根据引理2，可得(9)式与(4)式等价，故定理1得证。

下面将讨论在状态反馈控制器增益给定的前提下，增加状态信号量化后的闭环系统(3)的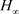性能的分析方法。

当考虑状态信号的量化时，量化控制器设计如下：

$\tilde{u}\left(k\right)=K\tilde{x}\left(k\right)$ (10)

其中 $\tilde{x}\left(k\right)\in R^p$ 是 $x\left(k\right)\in R^p$ 的量化信号。

定理2 设(4)式成立，并且量化器的范围 $M$ 足够大，使得

$M>\frac{1}{\eta }$

为量化控制器(10)设计参数 $\mu \left(k\right)$，其调整方式如下：

$\frac{1}{M}\left|\text{x}\left(k\right)\right|\le \mu \left(k\right)\le \eta \left|\text{x}\left(k\right)\right|$ (11)

其中，

$\eta =\frac{{\lambda }_{\min }\left(\text{R}\right)}{\phi \left(\varsigma +\sqrt{{\varsigma }^2+\tau ({\lambda }_{\min }\left(\text{R}\right)}\right)}$ (12)

$\Vert \left(h\text{I}+h^2{\left(\text{A}+\text{BK}\right)}^{\text{T}}\right)\text{PBK}\Vert <\varsigma$ (13)

$\Vert 2h^2{\left(\text{BK}\right)}^{\text{T}}\text{PBK}\Vert <\tau$ (14)

则具有参数调整方式(11)的量化控制器(10)可以使得闭环系统(3)渐进稳定且满足 $H_{\infty }$ 性能指标 $\gamma$。

证明 考虑量化控制器 $\tilde{u}\left(k\right)=K\tilde{x}\left(k\right)$，其中，

$\tilde{x}\left(k\right)=q_{\mu }\left(\text{x}\left(k\right)\right)=\mu \left(k\right)q\left(\frac{\text{x}\left(k\right)}{\mu (\; k\; )}\right)$

其中 $q_{\mu }(\cdot )$ 是一个具有一般形式的单参数族动态量化器， $\mu \left(k\right)$ 表示动态量化参数。假设存在标量 $M>0$， $\phi >0$，满足，若 $\left|x\left(k\right)\right|\le M$，则 $\left|q_{\mu }\left(x\left(k\right)\right)-x\left(k\right)\right|\le \phi$，则表明在量化器不饱和时，其提供了量化误差的界限， $M$ 表示量化器 $q_{\mu }(\cdot )$ 的量化范围， $\phi$ 表示量化误差界限。

下面，将量化控制器(10)代入Delta算子系统(1)中。得到：

$\begin{array}{l}\delta \text{x}\left(k\right)=A\text{x}\left(k\right)+BK\tilde{x}\left(k\right)+E\text{ω}\left(k\right)\\ =A\text{x}\left(k\right)+BK\mu \left(k\right)q\left(\frac{\text{x}\left(k\right)}{\mu \left(k\right)}\right)+E\text{ω}\left(k\right)\\ =A\text{x}\left(k\right)+BK\mu \left(k\right)q\left(\frac{\text{x}\left(k\right)}{\mu \left(k\right)}\right)+BK\text{x}\left(k\right)-\mu \left(k\right)BK\frac{\text{x}\left(k\right)}{\mu \left(k\right)}+E\text{ω}\left(k\right)\\ =\left(A+BK\right)\text{x}\left(k\right)+E\text{ω}\left(k\right)+BK\left[\mu \left(k\right)\left(q\left(\frac{\text{x}\left(k\right)}{\mu \left(k\right)}\right)-\frac{\text{x}\left(k\right)}{\mu \left(k\right)}\right)\right]\\ =\left(A+BK\right)\text{x}\left(k\right)+E\text{ω}\left(k\right)+BK\text{e}\left(k\right)\end{array}$ (15)

故得到以下闭环系统：

$\{\begin{array}{l}\delta \text{x}\left(k\right)=\left(A+BK\right)\text{x}\left(k\right)+E\text{ω}\left(k\right)+BK\text{e}\left(k\right)\\ \text{y}\left(k\right)=\text{Cx}(\; k\; )\end{array}$

其中， $\text{e}\left(k\right)=\left[\mu \left(k\right)\left(q\left(\frac{\text{x}\left(k\right)}{\mu \left(k\right)}\right)-\frac{\text{x}\left(k\right)}{\mu \left(k\right)}\right)\right]$。

根据Lapunov函数和Delta算子定义可得，

$\begin{array}{l}\text{x}\left(k+1\right)=h\delta \text{x}\left(k\right)+\text{x}\left(k\right)\\ =h\left[\left(\text{A}+\text{BK}\right)\text{x}\left(k\right)+\text{Eω}\left(k\right)+\text{BKe}\left(k\right)\right]+\text{x}\left(k\right)\\ =\left[\text{I}+h\left(\text{A}+\text{BK}\right)\right]\text{x}\left(k\right)+h\text{Eω}\left(k\right)+h\text{BKe}(\; k\; )\end{array}$

故

$\begin{array}{l}\tilde{\Theta }={\text{y}}^{\text{T}}\left(k\right)\text{y}\left(k\right)-{\gamma }^2{\text{ω}}^{\text{T}}\left(k\right)\text{ω}\left(k\right)+\Delta V\left(\text{x}\left(k\right)\right)\\ ={\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\\ \text{e}\left(k\right)\end{array}\right]}^{\text{T}}({\left[\begin{array}{ccc}\text{C}& 0& 0\end{array}\right]}^{\text{T}}\left[\begin{array}{ccc}\text{C}& 0& 0\end{array}\right]-{\left[\begin{array}{ccc}0& \gamma \text{I}& 0\end{array}\right]}^{\text{T}}\left[\begin{array}{ccc}0& \gamma \text{I}& 0\end{array}\right]\underset{}{\overset{}{\underset{}{\overset{}{}}}}\\ +{\left[\begin{array}{ccc}\text{I}+h\left(\text{A}+\text{BK}\right)& h\text{E}& h\text{BK}\end{array}\right]}^{\text{T}}\text{P}\left[\begin{array}{ccc}\text{I}+h\left(\text{A}+\text{BK}\right)& h\text{E}& h\text{BK}\end{array}\right]-\left[\begin{array}{ccc}\text{P}& 0& 0\\ *& *& 0\\ *& *& 0\end{array}\right])\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\\ \text{e}\left(k\right)\end{array}\right]\end{array}$

$\begin{array}{l}={\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\\ \text{e}\left(k\right)\end{array}\right]}^{\text{T}}(\left[\begin{array}{ccc}-\text{P}+{\text{C}}^{\text{T}}\text{C}& 0& 0\\ *& -{\gamma }^2\text{I}& 0\\ *& *& 0\end{array}\right]\\ +\left[\begin{array}{ccc}\left(\text{I}+h{\left(\text{A}+\text{BK}\right)}^{\text{T}}\right)\text{P}\left(\text{I}+h\left(\text{A}+\text{BK}\right)\right)& h\left(\text{I}+h{\left(\text{A}+\text{BK}\right)}^{\text{T}}\right)\text{PE}& h\left(\text{I}+h{\left(\text{A}+\text{BK}\right)}^{\text{T}}\right)\text{PBK}\\ \text{*}& h^2{\text{E}}^{\text{T}}\text{PE}& h^2{\text{E}}^{\text{T}}\text{PBK}\\ \text{*}& \text{*}& h^2{\left(\text{BK}\right)}^{\text{T}}\text{PBK}\end{array}\right])\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\\ \text{e}\left(k\right)\end{array}\right]\\ ={\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\\ \text{e}\left(k\right)\end{array}\right]}^{\text{T}}\left(\left[\begin{array}{cc}{\stackrel{\dot{}}{\Omega }}_{\text{2}}& \begin{array}{c}0\\ 0\end{array}\\ \begin{array}{cc}*& *\end{array}& 0\end{array}\right]+\left[\begin{array}{cc}{\Omega }_1& \begin{array}{c}h\left(\text{I}+h{\left(\text{A}+\text{BK}\right)}^{\text{T}}\right)\text{PBK}\\ h^2{\text{E}}^{\text{T}}\text{PBK}\end{array}\\ \begin{array}{cc}\text{*}& \text{*}\end{array}& h^2{\left(\text{BK}\right)}^{\text{T}}\text{PBK}\end{array}\right]\right)\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\\ \text{e}\left(k\right)\end{array}\right]\end{array}$

$\begin{array}{l}={\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]}^{\text{T}}\left({\stackrel{\dot{}}{\Omega }}_{\text{2}}+{\Omega }_1\right)\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]+h{\text{e}}^{\text{T}}\left(k\right){\left(\text{BK}\right)}^{\text{T}}\text{P}\left(\text{I}+h\left(\text{A}+\text{BK}\right)\right)\text{x}\left(k\right)+h^2{\text{e}}^{\text{T}}\left(k\right){\left(\text{BK}\right)}^{\text{T}}\text{PEω}\left(k\right)\\ +h^2{\text{e}}^{\text{T}}\left(k\right){\left(\text{BK}\right)}^{\text{T}}\text{PBKe}\left(k\right)+h{\text{x}}^{\text{T}}\left(k\right)\left(\text{I}+h{\left(\text{A}+\text{BK}\right)}^{\text{T}}\right)\text{PBKe}\left(k\right)+h^2{\text{ω}}^{\text{T}}\left(k\right){\text{E}}^{\text{T}}\text{PBKe}\left(k\right)\end{array}$ (16)

其中 ${\Omega }_1$ 与定理1证明中相同， ${\stackrel{\dot{}}{\Omega }}_{\text{2}}=\left[\begin{array}{cc}-\text{P}+{\text{C}}^{\text{T}}\text{C}& 0\\ *& -{\gamma }^2\text{I}\end{array}\right]$。

由此可得，

$\begin{array}{l}\tilde{\Theta }\le {\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]}^{\text{T}}\left({\stackrel{\dot{}}{\Omega }}_{\text{2}}+{\Omega }_1\right)\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]+h{\text{e}}^{\text{T}}\left(k\right){\left(\text{BK}\right)}^{\text{T}}\text{P}\left(\text{I}+h\left(\text{A}+\text{BK}\right)\right)\text{x}\left(k\right)+h^2{\text{ω}}^{\text{T}}\left(k\right){\text{E}}^{\text{T}}\text{PEω}\left(k\right)\\ +h^2{\text{e}}^{\text{T}}\left(k\right){\left(\text{BK}\right)}^{\text{T}}\text{PBKe}\left(k\right)+h{\text{x}}^{\text{T}}\left(k\right)\left(\text{I}+h{\left(\text{A}+\text{BK}\right)}^{\text{T}}\right)\text{PBKe}\left(k\right)+h^2{\text{e}}^{\text{T}}\left(k\right){\left(\text{BK}\right)}^{\text{T}}\text{PBKe}\left(k\right)\\ ={\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]}^{\text{T}}\left({\Omega }_{\text{2}}+{\Omega }_{\text{1}}\right)\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]+h{\text{e}}^{\text{T}}\left(k\right){\left(\text{BK}\right)}^{\text{T}}\text{P}\left(\text{I}+h\left(\text{A}+\text{BK}\right)\right)\text{x}\left(k\right)\\ +h{\text{x}}^{\text{T}}\left(k\right)\left(\text{I}+h{\left(\text{A}+\text{BK}\right)}^{\text{T}}\right)\text{PBKe}\left(k\right)+2h^2{\text{e}}^{\text{T}}\left(k\right){\left(\text{BK}\right)}^{\text{T}}\text{PBKe}\left(k\right)\end{array}$ (17)

其中 ${\Omega }_1$ 、 ${\Omega }_{\text{2}}$ 与定理1证明中相同。

注1 对于正定矩阵 $\text{R}$， ${\lambda }_{\min }\left(\text{R}\right){\left|\text{x}\left(k\right)\right|}^2\le {\text{x}}^{\text{T}}\left(k\right)\text{Rx}\left(k\right)\le {\lambda }_{\max }\left(\text{R}\right){\left|\text{x}\left(k\right)\right|}^2$ 对任意 $\text{x}\left(k\right)$ 成立。

考虑定理1证明中条件 $\Theta <-\text{R}$，可以得到，

${\Omega }_1+{\Omega }_{\text{2}}<-\text{R}$

则(17)式等价于

$\begin{array}{l}\tilde{\Theta }<{\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]}^{\text{T}}\left(-\text{R}\right)\left[\begin{array}{c}\text{x}\left(k\right)\\ \text{ω}\left(k\right)\end{array}\right]+h{\text{e}}^{\text{T}}\left(k\right){\left(\text{BK}\right)}^{\text{T}}\text{P}\left(\text{I}+h\left(\text{A}+\text{BK}\right)\right)\text{x}\left(k\right)\\ +h{\text{x}}^{\text{T}}\left(k\right)\left(\text{I}+h{\left(\text{A}+\text{BK}\right)}^{\text{T}}\right)\text{PBKe}\left(k\right)+2h^2{\text{e}}^{\text{T}}\left(k\right){\left(\text{BK}\right)}^{\text{T}}\text{PBKe}\left(k\right)\\ <-{\lambda }_{\min }\left(\text{R}\right){\left|\text{x}\left(k\right)\right|}^2+2\left|\text{x}\left(k\right)\right|{\alpha }_1\left|\text{e}\left(k\right)\right|+{\alpha }_2{\left|\text{e}\left(k\right)\right|}^2\end{array}$

其中 ${\alpha }_1=\Vert \left(h\text{I}+h^2{\left(\text{A}+\text{BK}\right)}^{\text{T}}\right)\text{PBK}\Vert$， ${\alpha }_2=\Vert 2h^2{\left(\text{BK}\right)}^{\text{T}}\text{PBK}\Vert$。

根据(13)式和(14)式，可得，

$\begin{array}{l}\tilde{\Theta }<-{\lambda }_{\min }\left(\text{R}\right){\left|\text{x}\left(k\right)\right|}^2+2\left|\text{x}\left(k\right)\right|{\alpha }_1\left|\text{e}\left(k\right)\right|+{\alpha }_2{\left|\text{e}\left(k\right)\right|}^2\\ <-{\lambda }_{\min }\left(\text{R}\right){\left|\text{x}\left(k\right)\right|}^2+2\left|\text{x}\left(k\right)\right|\varsigma \mu \left(k\right)\phi +\tau \mu {\left(k\right)}^2{\phi }^2\\ \text{=}-{\lambda }_{\min }\left(\text{R}\right)\left({\left|\text{x}\left(k\right)\right|}^2-\frac{2\left|\text{x}\left(k\right)\right|\varsigma \mu \left(k\right)\phi }{{\lambda }_{\min }\left(\text{R}\right)}-\frac{\tau \mu {\left(k\right)}^2{\phi }^2}{{\lambda }_{\min }\left(\text{R}\right)}\right)\\ =-{\lambda }_{\min }\left(\text{R}\right)\left(\left|\text{x}\left(k\right)\right|-\frac{\varsigma +\sqrt{{\varsigma }^2+\tau {\lambda }_{\min }\left(\text{R}\right)}}{{\lambda }_{\min }\left(\text{R}\right)}\mu \left(k\right)\phi \right)\times \left(\left|\text{x}\left(k\right)\right|-\frac{\varsigma -\sqrt{{\varsigma }^2+\tau {\lambda }_{\min }\left(\text{R}\right)}}{{\lambda }_{\min }\left(\text{R}\right)}\mu \left(k\right)\phi \right)\end{array}$

根据(11)式和(12)式可得，当

$\left|\text{x}\left(k\right)\right|>\frac{\varsigma +\sqrt{{\varsigma }^2+\tau {\lambda }_{\min }\left(\text{R}\right)}}{{\lambda }_{\min }\left(\text{R}\right)}\mu \left(k\right)\phi$

时，意味着 $\tilde{\Theta }<0$，故定理2得证。

4. 数值算例

考虑一个采样周期为 $h=0.0\text{5}$ 的Delta算子系统，具体参数如下，

$\text{A}=\left[\begin{array}{cc}-\text{0}\text{.0756}& -\text{0}\text{.0778}\\ \text{1}\text{.1022}& 0.1986\end{array}\right]$， $\text{B}=\left[\begin{array}{cc}0.6077& 0.1\\ 0.9768& 0.0019\end{array}\right]=\text{Q}$， $\text{E}=\left[\begin{array}{c}0.5721\\ 0.0211\end{array}\right]$， $\text{C}=\left[\begin{array}{cc}1& 0\end{array}\right]$

并且设定 $H_{\infty }$ 性能指标 $\gamma =2$， $\xi =5$。利用MATLAB中LMI工具箱中的求解器feasp对(4)式进行求解，得到，

$\text{P}=\left[\begin{array}{cc}\text{3}\text{.4848}& -\text{0}\text{.3974}\\ -\text{0}\text{.3974}& \text{93}\text{.0087}\end{array}\right]$， $\text{G}=\left[\begin{array}{cc}-\text{5}\text{.5967}& -\text{10}\text{.7701}\\ -\text{4}\text{.5307}& \text{22}\text{.3639}\end{array}\right]$， $\text{U}=\left[\begin{array}{l}\text{13}\text{.40253}\text{.8044}\\ \text{4}\text{.701417}\text{.5896}\end{array}\right]$，

$\text{R}=\left[\begin{array}{ccc}\text{1}\text{.191}1& -\text{10}\text{.6067}& -0.0061\\ \text{11}\text{.9317}& \text{4}\text{.704}1& 0.0325\\ \ast & \ast & 0.8261\end{array}\right]$

进而求得状态反馈控制器

$\text{K}={\text{U}}^{-1}\text{G}=\left[\begin{array}{cc}-\text{0}\text{.3727}& -\text{1}\text{.260}1\\ -\text{0}\text{.1579}& \text{1}\text{.6082}\end{array}\right]$

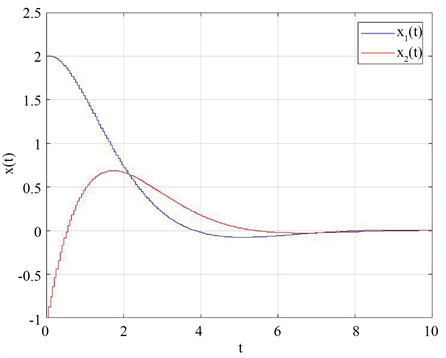
Figure 1. The state trajectories of the closed-loop system

图1. 闭环系统的状态轨迹

设系统初始状态 ${\text{x}}_0={\left[\begin{array}{cc}2& -1\end{array}\right]}^{\text{T}}$，外部扰动 $\text{ω}=0.01\sin \left(k\right)$，得到闭环系统的状态轨迹如图1所示。