具有非光滑解的第三类时滞Volterra积分方程的Müntz配置法

Müntz Collocation Method for the Third-Kind Volterra Integral Equations with Proportional Delays and Non-Smooth Solutions

摘要: 本文运用Müntz配置法求解具有非光滑解的第三类时滞Volterra积分方程并给出收敛性分析。首先选取合适的分数次多项式空间作为近似解空间，使得数值解更精准地逼近方程的解析解，再用带权的分数次Jacobi高斯求积公式近似积分算子得到全离散格式。其次通过理论分析给出数值格式在L_∞和带权L²_ω^α,β,λ范数下的误差估计，最后通过数值实验验证了数值格式的谱精度。

Abstract: In this paper, the Müntz-collocation method is used to solve the third-kind Volterra integral equation with delay and the convergence analysis is given. Firstly, the proper fractional polynomial space is selected as the approximate solution space to make the numerical solution more accurately approach the analytic solution of the equation. Then, the fractional Jacobi Gaussian quadrature formula with weight is used to approximate the integral operator to get the fully discrete scheme. Secondly, the error estimations of the numerical scheme under L_∞ norm and the weighted L²_ω^α,β,λ norm are given by theoretical analysis. Finally, the spectral accuracy of the numerical scheme is verified by numerical experiments.

1. 引言

本文主要考虑如下时滞第三类Volterra积分方程：

$t^{\nu }y\left(t\right)={\displaystyle {\int }_0^{qt}{\left(qt-\delta \right)}^{-\mu }}K\left(t,\delta \right)y\left(\delta \right)\text{d}\delta +f\left(t\right),t\in I:=\left[0,T\right],$ (1)

其中 $\nu >0$， $\mu \in \left[0,1\right)$，函数 $f\left(t\right)=t^{\nu }g\left(t\right),f\in C\left(I\right)$，核函数 $K(t,\delta )$ 具有分解形式

$K\left(t,\delta \right)=\{\begin{array}{l}{\delta }^{\mu +\nu -1}H\left(t,\delta \right),\mu +\nu \ge 1，\\ H\left(t,\delta \right),\mu +\nu <1.\end{array}$

Volterra积分方程(VIEs)在生物学、控制问题、人口动力学等方面都有广泛应用，其中基于第一、二类Volterra积分方程的理论和算法研究已相对成熟 [1]，而第三类Volterra积分方程由于积分算子结构更加复杂，研究进展相对缓慢。1910年，Evans [2] 首次提出第三类VIEs的一般形式。然而直到2015年，Seyed，Alleai等学者 [3] 证明了第三类VIEs的解的存在性、唯一性、正则性后，第三类VIEs才受到更多学者关注。2017年，Seyed，Alleai等在文献 [4] 中采用样条配置法得到该方程的近似解。随后，关于第三类VIEs的理论和算法研究得到快速发展。2019年，宋等 [5] 在分片多项式空间中用配置法求解了非线性第三类VIEs，同年Shayanfard等 [6] 采用多步配置法求解第三类VIEs。2020年，蔡 [7] 提出基于算子分解法的谱Legendre-Galerkin法求解第三类VIEs，并给出稳定性和收敛性分析。2021年，宋等 [8] 采用梯度网格求解了具有时滞项的第三类VIEs。2021年，马等 [9] 用Chebyshev谱配置法求解了具有非光滑解的第三类Volterra 积分方程并给出了严格的收敛性分析，同年马等在文献 [10] 中采用Legendre配置法求解具有非光滑解的第三类Volterra积分微分方程。

为了简化模型，令 $\delta =qs$，方程(1)可转化为

$y\left(t\right)={\mathcal{V}}_{\mu ,\nu ,q}y\left(t\right)+g\left(t\right),t\in I:=\left[0,1\right],$ (2)

其中 ${\mathcal{V}}_{\mu ,\nu ,q}y\left(t\right)=q{\displaystyle {\int }_0^t{t}^{-\nu }}{\left(qt-qs\right)}^{-\mu }K\left(t,qs\right)y\left(qs\right)\text{d}s$， $g\left(t\right)=t^{-\nu }f\left(t\right)$。从文献 [4] [11] 和 [12] 可知当 $\mu +\nu \ge 1$ 且 $H\left(0,0\right)\ne 0$ 时积分算子 ${\mathcal{V}}_{\mu ,\nu ,q}$ 是非紧致的，然而当 $\mu +\nu <0$ 或者当 $\mu +\nu \ge 1$ 且 $H\left(0,0\right)=0$ 时，积分算子 ${\mathcal{V}}_{\mu ,\nu ,q}$ 是从 $C\left(I\right)$ 到 $C\left(I\right)$ 的紧算子。

2019年，侯等在 [12] 中提出了新的导数定义，证明了分数次Jacobi多项式在新导数定义下能继承经典Jacobi多项式的基本性质，并指出用Müntz配置法求解一般弱奇异Volterra积分方程具有显著优势。本文基于分数次Jacobi多项式配置点的Müntz配置法求(2)，并在带权的Sobolev空间中研究该配置法的收敛性，最后通过数值算例验证理论结论的有效性。

2. 预备知识及离散格式

2.1. 预备知识

为了构建分数次Jacobi配置法的离散格式。我们首先引入分数次多项式空间作为近似解空间，其次引入新的导数定义使得分数次Jacobi多项式能继承经典Jacobi多项式的基本性质，如正交性等。最后定义加权Sobolev空间下的正交投影算子和插值算子，为第四节的收敛性分析提供理论依据。

定义2.1 [12] 定义分数次多项式空间

${\mathbb{P}}_n^{\lambda }\left(I\right):=\left\{1,t^{\lambda },t^{2\lambda },t^{3\lambda },\cdots ,t^{n\lambda }\right\},0<\lambda \le 1,$

和n次分数次Jacobi多项式

$J_n^{\alpha ,\beta ,\lambda }\left(t\right)=J_n^{\alpha ,\beta }\left(2t^{\lambda }-1\right),\forall t\in I,\alpha ,\beta >-1,$

其中 $J_n^{\alpha ,\beta }\left(t\right)$ 是标准Jacobi多项式， $J_n^{\alpha ,\beta ,\lambda }\left(t\right)$ 是关于权函数 ${\omega }^{\alpha ,\beta ,\lambda }\left(t\right)=\lambda {\left(1-t^{\lambda }\right)}^{\alpha }{t}^{\left(\beta +1\right)\lambda -1}$ 正交的分数次Jacobi多项式。

定义2.2 [12] 广义Lagrange基函数

$l_{j,\lambda }^{\alpha ,\beta }\left(t\right)={\displaystyle \underset{i=0,i\ne j}{\overset{N}{\prod }}\frac{t^{\lambda }-t_i^{\lambda }}{t_j^{\lambda }-t_i^{\lambda }}},0\le j\le N,$

其中 ${\left\{t_j\right\}}_{j=0}^N$ 是N + 1个分数次Jacobi高斯点。由此广义Lagrange插值算子定义为 ${\mathcal{I}}_{N,\lambda }^{\alpha ,\beta }:C\left(I\right)\to {\mathbb{P}}_N^{\lambda }(\; I\; )$

${\mathcal{I}}_{N,\lambda }^{\alpha ,\beta }y\left(t\right)={\displaystyle \underset{j=0}{\overset{N}{\sum }}{l}_{j,\lambda }^{\alpha ,\beta }}\left(t\right)y\left(t_j\right).$

定义2.3 [12] 如果 $0<\lambda \le 1$， $k\ge 1$，则k次新导数 $D_{\lambda }^{k}y\left(t\right)$ 定义为

$D_{\lambda }^{k}y\left(t\right)=\stackrel{k}{\stackrel{︷}{D_{\lambda }^1\cdot D_{\lambda }^1\cdots D_{\lambda }^1}}y\left(t\right),D_{\lambda }^{1}y\left(t\right)=\frac{\text{d}}{\text{d}{t}^{\lambda }}y\left(t\right)=\frac{t^{1-\lambda }}{\lambda }{y}^{\prime }\left(t\right).$

由文献 [12] 可知，在新的k次导数定义下，分数次Jacobi多项式能很好的继承经典Jacobi多项式的正交性。最后，我们定义带权 $L_{{\omega }^{\alpha ,\beta ,\lambda }}^2$ 空间及其内积和范数

$\begin{array}{l}{L}_{{\omega }^{\alpha ,\beta ,\lambda }}^2=\left\{y|{\displaystyle {\int }_0^1{\left|y\left(t\right)\right|}^2{\omega }^{\alpha ,\beta ,\lambda }\left(t\right)\text{d}t}<+\infty \right\},\\ {\left(u,v\right)}_{{\omega }^{\alpha ,\beta ,\lambda }}={\displaystyle {\int }_0^{1}u}\left(t\right)v\left(t\right){\omega }^{\alpha ,\beta ,\lambda }\left(t\right)\text{d}t,{\Vert u\Vert }_{{\omega }^{\alpha ,\beta ,\lambda }}={\left(u,u\right)}_{{\omega }^{\alpha ,\beta ,\lambda }}^{\frac{1}{2}}.\end{array}$

以及分数次Jacobi加权Sobolev空间及其内积、范数和半范数

$\begin{array}{l}{B}_{\alpha ,\beta }^{m,\lambda }\left(I\right)=\left\{y|D_{\lambda }^{k}y\in L_{{\omega }^{\alpha +k,\beta +k,\lambda }}^2\left(I\right),0\le k\le m\right\},m\in N,\\ {\left(y,v\right)}_{B_{\alpha ,\beta }^{m,\lambda }}={\displaystyle \underset{k=0}{\overset{m}{\sum }}{\left(D_{\lambda }^{k}y,D_{\lambda }^{k}v\right)}_{{\omega }^{\alpha +k,\beta +k,\lambda }}},{\Vert y\Vert }_{B_{\alpha ,\beta }^{m,\lambda }}={\left(y,y\right)}_{B_{\alpha ,\beta }^{m,\lambda }}^{\frac{1}{2}},\\ {\left|y\right|}_{B_{\alpha ,\beta }^{m,\lambda }}={\Vert D_{\lambda }^{m}y\Vert }_{0,{\omega }^{\alpha +m,\beta +m,\lambda }}:={\left(D_{\lambda }^{m}y,D_{\lambda }^{m}y\right)}_{{\omega }^{\alpha +m,\beta +m,\lambda }}.\end{array}$

2.2. 离散格式

Müntz配置法是将分数次多项式空间作为近似解空间，也就是寻找 $y_N^{\lambda }\in {\mathbb{P}}_N^{\lambda }\left(I\right)$ 使得方程(2)在分数次Jacobi配置点 ${\left\{t_i\right\}}_{i=0}^N$ 上恒成立，即

$y_N^{\lambda }\left(t_i\right)=\left({\mathcal{V}}_{\mu ,\nu ,q}{y}_N^{\lambda }\right)\left(t_i\right)+g\left(t_i\right),i=0,\cdots ,N.$ (3)

为了利用分数次Jacobi多项式的正交性求解上述方程，引入变量变换 $s={\tau }_i\left(\theta \right)=t_i{\theta }^{\frac{1}{\lambda }}$，则(3)中的积分项

$\begin{array}{l}{\mathcal{V}}_{\mu ,\nu ,q}{y}_N^{\lambda }\left(t_i\right)=q{\displaystyle {\int }_0^t{t}_i^{-\nu }}{\left(q{t}_i-qs\right)}^{-\mu }K\left(t_i,qs\right)y_N^{\lambda }\left(qs\right)\text{d}s\\ ={\displaystyle {\int }_0^1\frac{1}{\lambda }}{t}_i^{1-\mu -\nu }{q}^{1-\mu }{\left(1-{\theta }^{\frac{1}{\lambda }}\right)}^{-\mu }K\left(t_i,q{\tau }_i\left(\theta \right)\right)y_N^{\lambda }\left(q{\tau }_i\left(\theta \right)\right){\theta }^{\frac{1}{\lambda }-1}\text{d}\theta \\ =:{\left(\bar{K}\left(t_i,q{\tau }_i\left(\theta \right)\right),y_N^{\lambda }\left(q{\tau }_i\left(\theta \right)\right)\right)}_{{\omega }^{-\mu ,\varphi \left(\mu ,\nu \right),1}},\end{array}$ (4)

其中

$\begin{array}{l}\bar{K}\left(t,q{\tau }_i\left(\theta \right)\right)=\{\begin{array}{l}\frac{1}{\lambda }{q}^{\nu }{\left(\frac{1-{\theta }^{\frac{1}{\lambda }}}{1-\theta }\right)}^{-\mu }{\theta }^{\lceil \frac{\mu +\nu }{\lambda }\rceil -1}H\left(t,q{\tau }_i\left(\theta \right)\right),\mu +\nu \ge 1,\\ \frac{1}{\lambda }{t}^{1-\mu -\nu }{q}^{1-\mu }{\left(\frac{1-{\theta }^{\frac{1}{\lambda }}}{1-\theta }\right)}^{-\mu }{\theta }^{\lceil \frac{1}{\lambda }\rceil -1}H\left(t,q{\tau }_i\left(\theta \right)\right),\mu +\nu <1,\end{array}\\ \varphi \left(\mu ,\nu \right)=\{\begin{array}{l}\frac{\mu +\nu }{\lambda }-\lceil \frac{\mu +\nu }{\lambda }\rceil ,\mu +\nu \ge 1,\\ \frac{1}{\lambda }-\lceil \frac{1}{\lambda }\rceil ,\mu +\nu <1,\end{array}\end{array}$ (5)

$\lceil \cdot \rceil$ 表示上取整函数。

对于给定的N > 0，设 ${\left\{{\theta }_k,w_k\right\}}_{k=0}^N$ 是N + 1个分数次Jacobi高斯点和相应权值，则存在如下分数次Jacobi-Guass求积公式：

${\displaystyle {\int }_0^{1}f}\left(t\right){\omega }^{\alpha ,\beta ,\lambda }\left(t\right)\text{d}t\approx {\displaystyle \underset{k=0}{\overset{N}{\sum }}f}\left({\theta }_k\right){\omega }_k,$

因此利用分数次Jacobi-Guass求积公式近似积分项(4)，可得

${\left(\bar{K}\left(t_i,q{\tau }_i\left(\theta \right)\right),y_N^{\lambda }\left(q{\tau }_i\left(\theta \right)\right)\right)}_{{\omega }^{-\mu ,\varphi \left(\mu ,\nu \right),1}}\approx {\displaystyle \underset{k=0}{\overset{N}{\sum }}\bar{K}}\left(t_i,q{\tau }_i\left({\theta }_k\right)\right)y_N^{\lambda }\left(q{\tau }_i\left({\theta }_k\right)\right){\omega }_k.$

为了方便，我们令

$\left({\mathcal{V}}_{\mu ,\nu ,q}^N{y}_N^{\lambda }\right)\left(t_i\right):={\left(\bar{K}\left(t_i,q{\tau }_i\left(\theta \right)\right),y_N^{\lambda }\left(q{\tau }_i\left(\theta \right)\right)\right)}_{N,{\omega }^{-\mu ,\varphi \left(\mu ,\nu \right),1}}\approx {\displaystyle \underset{k=0}{\overset{N}{\sum }}\bar{K}}\left(t_i,q{\tau }_i\left({\theta }_k\right)\right)y_N^{\lambda }\left(q{\tau }_i\left({\theta }_k\right)\right){\omega }_k.$

综上所述，分数次Jacobi谱配置法的数值解 $y_N^{\lambda }\left(t\right)={\displaystyle \underset{j=0}{\overset{N}{\sum }}{y}_j}{l}_{j,\lambda }^{\alpha ,\beta }\left(t\right)\in {\mathbb{P}}_N^{\lambda }\left(I\right)$ 满足全离散格式

$y_N^{\lambda }\left(t_i\right)=\left({\mathcal{V}}_{\mu ,\nu ,q}^N{y}_N^{\lambda }\right)\left(t_i\right)+g\left(t_i\right),i=0,1,\cdots ,N,$ (6)

其等价矩阵形式为

$Y=AY+F,$

$\begin{array}{l}Y={\left(y_0,y_1,\cdots ,y_N\right)}^{\text{T}}\text{,}F={\left(g\left(t_0\right),g\left(t_1\right),\cdots ,g\left(t_N\right)\right)}^{\text{T}},\\ a_{i,j}={\displaystyle \underset{k=0}{\overset{N}{\sum }}\bar{K}}\left(t_i,q{\tau }_i\left({\theta }_k\right)\right)l_{j,\lambda }^{\alpha ,\beta }\left(q{\tau }_i\left({\theta }_k\right)\right){\omega }_k,A={\left(a_{i,j}\right)}_{i,j=0}^N.\end{array}$

3. 主要引理

本节我们介绍在加权Sobolev空间下的投影算子、插值算子、分数次Jacobi多项式等概念的重要性质，以及在下节收敛性分析证明中需要用到的重要引理。

引理3.1 [12] 如果 $-1<\alpha ,\beta \le -\frac{1}{2}$，那么对一切 $y\left(t^{\frac{1}{\lambda }}\right)\in B_{\alpha ,\beta }^{m,1}\left(I\right)$，有

$\begin{array}{l}\Vert y-{\mathcal{I}}_{N,\lambda }^{\alpha ,\beta }y\Vert \le C{N}^{\frac{1}{2}-m}{\Vert {\partial }_t^{m}y\left(t^{\frac{1}{\lambda }}\right)\Vert }_{0,{\omega }^{\alpha +m,\beta +m,1}},\\ {\Vert D_{\lambda }^l\left(y-{\mathcal{I}}_{N,\lambda }^{\alpha ,\beta }y\right)\Vert }_{0,{\omega }^{\alpha +l,\beta +l,\lambda }}\le C{N}^{l-m}{\Vert {\partial }_t^{m}y\left(t^{\frac{1}{\lambda }}\right)\Vert }_{0,{\omega }^{\alpha +m,\beta +m,1}}.\end{array}$

引理3.2 [12] [13] 令 ${\left\{l_{j,\lambda }^{\alpha ,\beta }\left(t\right)\right\}}_{j=0}^N$ 是以N + 1个分数次Jacobi多项式高斯点 ${\left\{t_i\right\}}_{i=0}^N$ 为插值基点的拉格朗日插值基函数，则

$\begin{array}{l}{\Vert {\mathcal{I}}_{N,\lambda }^{\alpha ,\beta }\Vert }_{\infty }={\max }_{t\in I}{\displaystyle \underset{j=0}{\overset{N}{\sum }}\left|l_{j,\lambda }^{\alpha ,\beta }\left(t\right)\right|}=\{\begin{array}{l}O\left(\log N\right),-1<\alpha ,\beta \le -\frac{1}{2},\\ O\left(N^{\lambda }\right),\lambda =\max \left\{\alpha ,\beta \right\},其他,\end{array}\\ {\Vert {\mathcal{I}}_{N,\lambda }^{\alpha ,\beta }\Vert }_{{\omega }^{\alpha ,\beta }}={\Vert {\displaystyle \underset{j=0}{\overset{N}{\sum }}y}\left(t_j\right)l_{j,\lambda }^{\alpha ,\beta }\left(t\right)\Vert }_{{\omega }^{\alpha ,\beta }}\le C{\Vert y\Vert }_{\infty }.\end{array}$

引理3.3 [12] 假设 $m>1$， $\nu \in B_{\alpha ,\beta }^{m,1}\left(I\right)$，则对于分数次Jacobi-Guass插值有

$\left|{\left(y,\varphi \right)}_{{\omega }^{\alpha ,\beta ,1}}-{\left(y,\varphi \right)}_{N,{\omega }^{\alpha ,\beta ,1}}\right|\le C{N}^{-m}{\Vert {\partial }_t^{m}y\Vert }_{0,{\omega }^{\alpha +m,\beta +m,1}}{\Vert \varphi \Vert }_{0,{\omega }^{\alpha ,\beta ,1}},\forall \varphi \in {\mathbb{P}}_N^1,$

其中 ${\left(y,\varphi \right)}_{N,{\omega }^{\alpha ,\beta ,1}}={\displaystyle \underset{k=0}{\overset{N}{\sum }}y}\left(t_k\right)\varphi \left(t_k\right){\omega }_k$。

引理3.4 [9] 令 $L>0$， $y\left(t\right)$ 是在[0, 1]上的非负且局部可积函数，若 $y\left(t\right)$ 满足

$y\left(t\right)\le v\left(t\right)+L{\displaystyle {\int }_0^t{t}^{-\nu }}{\left(t-s\right)}^{-\mu }K\left(t,qs\right)y\left(qs\right)\text{d}s,$

则有

$y\left(t\right)\le v\left(t\right)+L{\displaystyle {\int }_0^t{t}^{-\nu }}{\left(t-s\right)}^{-\mu }K\left(t,qs\right)v\left(qs\right)\text{d}s.$

引理3.5 [13] 令r是非负整数， $\kappa \in \left(0,1\right)$，则存在常数C，使得对 $\forall y\left(t\right)\in {ℂ}^{r,\kappa }\left(I\right)$，存在函数 ${\daleth }_{N}y\in {\mathbb{P}}_N^1$ 满足

${\Vert y-{\daleth }_{N}y\Vert }_{\infty }\le C{N}^{-r-\kappa }{\Vert y\Vert }_{r,\kappa },$

其中 ${ℂ}^{r,\kappa }$ 是指数为 $\kappa$ 的r次Hölder连续函数

${\Vert y\Vert }_{r,\kappa }=\underset{{}_{0\le k\le r}}{\max }\underset{{}_{0\le t\le 1}}{\max }\left|{\partial }_t^{k}y\left(t\right)\right|+\underset{t\ne y}{\sup }\frac{\left|{\partial }_t^{r}y\left(t\right)-{\partial }_t^{r}y\left(t\right)\right|}{{\left|t-y\right|}^{\kappa }}.$

引理3.6 [9] 如果 $\mu <1$， $1-\mu -\nu +q>0$ 并且 $0<\kappa <\min \left\{1-\mu -\nu +q,1,1-\mu \right\}$，则存在依赖于 ${\Vert l\left(t,\cdot \right)\Vert }_{0,\kappa }$ 的C，使得对 $\forall y\left(t\right)\in C\left(I\right)$ 满足

$My\left(t\right)={\displaystyle {\int }_0^t{\left(t-s\right)}^{-\mu }}{t}^{\nu }{s}^{q}l\left(t,qs\right)y\left(qs\right)\text{d}s,$

则有

${\Vert My\left(t^{\frac{1}{\lambda }}\right)\Vert }_{0,\kappa }\le C{\Vert y\Vert }_{\infty }.$

4. 收敛性分析

本节研究该方法在 $L_{\infty }$ 和 $L_{{\omega }^{\alpha ,\beta ,\lambda }}^2$ 空间中的误差估计。不妨设 $e\left(t\right)=y\left(t\right)-y_N^{\lambda }\left(t\right)$ 为误差函数，则方程(6) 与方程(2)相减可得

$y\left(t_i\right)-y_i=\left({\mathcal{V}}_{\mu ,\nu ,q}e\right)\left(t_i\right)+I_i,$ (7)

其中 $I_i={\mathcal{V}}_{\mu ,\nu ,q}y\left(t_i\right)-{\mathcal{V}}_{\mu ,\nu ,q}^{N}y\left(t_i\right)$，接着将方程(7)两端同乘 $l_{i,\lambda }^{\alpha ,\beta }\left(t\right)$，并将i从0到N求和得

${\mathcal{I}}_{N,\lambda }^{\alpha ,\beta }y-y_N^{\lambda }=I_{N,\lambda }^{\alpha ,\beta }\left({\mathcal{V}}_{\mu ,\nu ,q}e\right)\left(t\right)+{\displaystyle \underset{i=0}{\overset{N}{\sum }}{l}_{i,\lambda }^{\alpha ,\beta }}\left(t\right)I_i,$

因此

$e\left(t\right)=\left({\mathcal{V}}_{\mu ,\nu ,q}\right)e\left(t\right)+{\displaystyle \underset{i=1}{\overset{3}{\sum }}{E}_i}\left(t\right),$

其中

$\begin{array}{l}{E}_1\left(t\right)=y\left(t\right)-{\mathcal{I}}_{N,\lambda }^{\alpha ,\beta }y\left(t\right),E_2\left(t\right)={\displaystyle \underset{i=0}{\overset{N}{\sum }}{l}_{i,\lambda }^{\alpha ,\beta }}\left(t\right)I_i,\\ E_3\left(t\right)=\left({\mathcal{I}}_{N,\lambda }^{\alpha ,\beta }-I\right)\left({\mathcal{V}}_{\mu ,\nu ,q}\right)e\left(t\right).\end{array}$ (8)

综上所述

$\left|e\left(t\right)\right|\le \left|{\displaystyle {\int }_0^t{t}^{-\nu }}{\left(t-s\right)}^{-\mu }K\left(t,qs\right)e\left(qs\right)\text{d}s\right|+\left|{\displaystyle \underset{i=0}{\overset{3}{\sum }}{E}_i}\left(t\right)\right|.$ (9)

定理4.1 假设 $-1<\alpha ,\beta \le -\frac{1}{2}$，核函数 $H\left(t,s\right)\in C^m\left(D\right)$，令y是问题(2)的解析解且 $y\left(t^{\frac{1}{\lambda }}\right)\in B_{\alpha ,\beta }^{m,1}\left(I\right)$， $y_N^{\lambda }$ 是采用离散格式(6)得到的近似解，则存在常数C，当N充分大时有

${\Vert y-y_N^{\lambda }\Vert }_{\infty }\le C{N}^{-m}\left(N^{\frac{1}{2}}{\Vert {\partial }_x^{m}y\left(t^{\frac{1}{\lambda }}\right)\Vert }_{0,{\omega }^{\alpha +m,\beta +m,1}}+\log N{K}^{\ast }{\Vert y\Vert }_{\infty }\right),$ (10)

其中

$K^{\ast }={\max }_{0\le i\le N}{\Vert {\partial }_{\theta }^{m}K\left(t_i,q{\tau }_i(\cdot )\right)\Vert }_{0,{\omega }^{m-\mu ,m+\varphi \left(\mu ,\nu \right),1}}.$ (11)

证明：由引理3.4中的Gronwall不等式可得

${\Vert e\left(t\right)\Vert }_{\infty }\le C{\displaystyle \underset{i=0}{\overset{3}{\sum }}{\Vert E_1\left(t\right)\Vert }_{\infty }}.$ (12)

由引理3.1、引理3.2、引理3.3可分别得到

$\begin{array}{l}{\Vert E_1\left(t\right)\Vert }_{\infty }={\Vert y\left(t\right)-I_{N,\lambda }^{\alpha ,\beta }y\left(t\right)\Vert }_{\infty }\le C{N}^{\frac{1}{2}-m}{\Vert {\partial }_t^{m}y\left(t^{\frac{1}{\lambda }}\right)\Vert }_{0,{\omega }^{\alpha +m,\beta +m,1}}.\\ {\max }_{1\le i\le N}\left|I_i\right|\le C{N}^{-m}{\max }_{1\le i\le N}{\Vert {\partial }_{\theta }^m\bar{K}\left(t,q{\tau }_i(\cdot )\right)\Vert }_{0,{\omega }^{m-\mu ,m+\varphi \left(\mu ,\nu \right),1}}{\max }_{1\le i\le N}{\Vert y_N^{\lambda }\left(q{\tau }_i(\cdot )\right)\Vert }_{0,{\omega }^{-\mu ,\varphi \left(\mu ,\nu \right),1}}\\ \le C{N}^{-m}{K}^{*}{\Vert y_N^{\lambda }\left(q{\tau }_i(\cdot )\right)\Vert }_{\infty }\le C{N}^{-m}{K}^{*}\left({\Vert y\Vert }_{\infty }+{\Vert e\Vert }_{\infty }\right),\\ {\Vert E_2\left(t\right)\Vert }_{\infty }={\Vert {\displaystyle \underset{i=0}{\overset{N}{\sum }}{l}_{i,\lambda }^{\alpha ,\beta }}\left(t\right)I_i\Vert }_{\infty }\le C\log N{N}^{-m}{K}^{*}\left({\Vert y\Vert }_{\infty }+{\Vert e\Vert }_{\infty }\right).\end{array}$

由于 $E_3$ 中积分算子的特殊性，我们分别讨论 $\mu +\nu \ge 1$ 和 $\mu +\nu <1$ 两种不同的情况下 ${\Vert E_3\Vert }_{\infty }$ 的范数估计。

当 $\mu +\nu \ge 1$ 时，因为 $H\left(t,s\right)\in C^m\left(D\right)$，则存在 $\xi \in \left(-1,t\right)$，满足一次Taylor展开式

$H\left(t,qs\right)=H\left(0,0\right)+\hat{H}\left(t,qs\right),$

其中

$\hat{H}\left(t,qs\right)=s{\frac{\text{d}H\left(s,qs\right)}{\text{d}s}|}_{s=\zeta }+\left(t-s\right){\partial }_{x}H\left(\xi ,qs\right).$

$\begin{array}{l}{E}_{3,1}\left(t\right)=\left({\mathcal{I}}_{N,\lambda }^{\alpha ,\beta }-I\right){\displaystyle {\int }_0^t{q}^{\nu }}{t}^{-\nu }{\left(t-s\right)}^{-\mu }{s}^{\mu +\nu -1}H\left(0,0\right)y\left(qs\right)\text{d}s,\\ E_{3,2}\left(t\right)=\left(I-{\mathcal{I}}_{N,\lambda }^{\alpha ,\beta }\right){\displaystyle {\int }_0^t{q}^{\nu }}{t}^{-\nu }{\left(t-s\right)}^{-\mu }{s}^{\mu +\nu -1}H\left(0,0\right)y_N^{\lambda }\left(qs\right)\text{d}s,\\ E_{3,3}\left(t\right)=\left({\mathcal{I}}_{N,\lambda }^{\alpha ,\beta }-I\right){\displaystyle {\int }_0^t{q}^{\nu }}{t}^{-\nu }{\left(t-s\right)}^{-\mu }{s}^{\mu +\nu -1}\hat{H}\left(t,qs\right)e\left(qs\right)\text{d}s.\end{array}$

则有

$E_3={\displaystyle \underset{i=1}{\overset{3}{\sum }}{E}_{3,i}}\left(t\right),$ (13)

接着根据引理3.1和Hardy不等式，参考文献 [12] 可以得到

$\begin{array}{l}{\Vert E_{3,1}\left(t\right)\Vert }_{\infty }\le C{N}^{\frac{1}{2}-m}{\Vert q^{\nu }{\partial }_t^m{\displaystyle {\int }_0^{t^{\frac{1}{\lambda }}}{\left(t^{\frac{1}{\lambda }}\right)}^{-\nu }}{\left(t^{\frac{1}{\lambda }}-s\right)}^{-\mu }{s}^{\mu +\nu -1}H\left(0,0\right)y\left(qs\right)\text{d}s\Vert }_{0,{\omega }^{\alpha +m,\beta +m,1}}\\ \le C{N}^{\frac{1}{2}-m}{\Vert \frac{q^{\nu }}{\lambda }{\displaystyle {\int }_0^1{\left(1-{\theta }^{\frac{1}{\lambda }}\right)}^{-\mu }}{\theta }^{\frac{\mu +\nu }{\lambda }-1}H\left(0,0\right){\partial }_t^{m}y\left(q{t}^{\frac{1}{\lambda }}{\theta }^{\frac{1}{\lambda }}\right)\text{d}\theta \Vert }_{0,{\omega }^{\alpha +m,\beta +m,1}}\\ \le C{N}^{\frac{1}{2}-m}{\Vert \frac{q^{\nu +\frac{m}{\lambda }}}{\lambda }{\displaystyle {\int }_0^1{\left(1-{\theta }^{\frac{1}{\lambda }}\right)}^{-\mu }}{\theta }^{\frac{\mu +\nu }{\lambda }+m-1}H\left(0,0\right){\partial }_{\tau }^{m}y\left({\tau }^{\frac{1}{\lambda }}\right)\text{d}\theta \Vert }_{0,{\omega }^{\alpha +m,\beta +m,1}}\\ \le C{N}^{\frac{1}{2}-m}{\Vert {\partial }_t^{m}y\left(t^{\frac{1}{\lambda }}\right)\Vert }_{0,{\omega }^{\alpha +m,\beta +m,1}}.\end{array}$ (14)

又因为 ${\displaystyle {\int }_0^t{q}^{\nu }}{t}^{-\nu }{\left(t-s\right)}^{-\mu }{s}^{\mu +\nu -1}H\left(0,0\right)y_N^{\lambda }\left(qs\right)\text{d}s\in {\mathbb{P}}_N^{\lambda }\left(I\right)$，所以

${\Vert E_{3,2}\left(t\right)\Vert }_{\infty }=0.$ (15)

因为

$\begin{array}{l}\hat{M}e\left(t\right)={\displaystyle {\int }_0^t{t}^{-\nu }}{\left(t-s\right)}^{-\mu }{s}^{\mu +\nu -1}\hat{H}\left(t,qs\right)e\left(qs\right)\text{d}s\\ ={\displaystyle {\int }_0^t{t}^{-\nu }}{\left(t-s\right)}^{-\mu }{s}^{\mu +\nu -1}{\frac{H\left(t,qs\right)}{\text{d}s}|}_{s=\eta }e\left(qs\right)\text{d}s\\ +{\displaystyle {\int }_0^t{t}^{-\nu }}{\left(t-s\right)}^{-\mu }{s}^{\mu +\nu -1}{\partial }_{x}H\left(\xi ,s\right)e\left(qs\right)\text{d}s,\end{array}$

接着我们令 ${\kappa }_1=1-\alpha$，再由引理3.2、引理3.5和引理3.6可得

$\begin{array}{l}{\Vert E_{3,3}\left(t\right)\Vert }_{\infty }=\underset{t\in I}{\max }\left|\left({\mathcal{I}}_{N,\lambda }^{\alpha ,\beta }-I\right)\left(\hat{M}e\right)\left(t\right)\right|=\underset{z^{1/\lambda }=t\in I}{\max }\left|\left({\mathcal{I}}_{N,1}^{\alpha ,\beta }-I\right)\left(\hat{M}e\right)\left(z^{\frac{1}{\lambda }}\right)\right|\\ ={\Vert \left({\mathcal{I}}_{N,1}^{\alpha ,\beta }-I\right)\left(\hat{M}e\right)\left(z^{\frac{1}{\lambda }}\right)\Vert }_{\infty }={\Vert \left({\mathcal{I}}_{N,1}^{\alpha ,\beta }-I\right)\left(I-{\daleth }_N\right)\left(\hat{M}e\right)\left(z^{\frac{1}{\lambda }}\right)\Vert }_{\infty }\\ \le C\left({\Vert {\mathcal{I}}_{N,1}^{\alpha ,\beta }\Vert }_{\infty }+1\right){\Vert \left(I-{\daleth }_N\right)\left(\hat{M}e\right)\left(z^{\frac{1}{\lambda }}\right)\Vert }_{\infty }\le C\log N{N}^{-{\kappa }_1}{\Vert \left(\hat{M}e\right)\left(z^{\frac{1}{\lambda }}\right)\Vert }_{0,{\kappa }_1}\\ \le C\log N{N}^{-{\kappa }_1}{\Vert e\Vert }_{\infty }.\end{array}$ (16)

最后，由(14)、(15)和(16)可知

${\Vert E_3\left(t\right)\Vert }_{\infty }\le C{\displaystyle \underset{k=1}{\overset{3}{\sum }}{\Vert E_{3,k}\left(t\right)\Vert }_{\infty }}\le C{N}^{\frac{1}{2}-m}{\Vert {\partial }_t^{m}y\left(t^{\frac{1}{\lambda }}\right)\Vert }_{0,{\omega }^{\alpha +m,\beta +m,1}}+C\log N{N}^{-{\kappa }_1}{\Vert e\Vert }_{\infty }.$

当 $\mu +\nu <1$ 时，相比于 $\mu +\nu \ge 1$ 情况下的积分算子，此情况下的积分算子构造较为简单，令 ${\kappa }_2=1-\mu -\nu$，类似(16)的证明可得

${\Vert E_3\left(t\right)\Vert }_{\infty }\le C\log N{N}^{-{\kappa }_2}{\Vert \left({\mathcal{V}}_{\mu ,\nu }e\right)\left(z^{\frac{1}{\lambda }}\right)\Vert }_{0,{\kappa }_2}\le C\log N{N}^{-{\kappa }_2}{\Vert e\Vert }_{\infty },$

通过上述证明过程，我们得到(10)式中的误差估计。

不失一般性，类似文献 [9] 定理4.2的证明过程可得(2.4)在加权 $L_{{\omega }^{\alpha ,\beta ,\lambda }}^2$ 范数下的误差估计。

定理4.2 假设 $-1<\alpha ,\beta \le -\frac{1}{2}$，核函数 $H\left(t,s\right)\in C^m\left(D\right)$，假设y是问题(2)的解析解且 $y\left(t^{\frac{1}{\lambda }}\right)\in B_{\alpha ,\beta }^{m,1}\left(I\right)$， $y_N^{\lambda }$ 是采用离散格式(6)得到的近似解，则存在常数C，当N充分大时有

${\Vert y-y_N^{\lambda }\Vert }_{0,{\omega }^{\alpha ,\beta ,\lambda }}\le C{N}^{-m}\left[\left(1+N^{\frac{1}{2}-{\kappa }_{\star }}\right){\Vert {\partial }_t^{m}y\left(t^{\frac{1}{\lambda }}\right)\Vert }_{0,{\omega }^{\alpha +m,\beta +m,1}}+K^{\ast }{\Vert y\Vert }_{\infty }\right],$ (17)

其中

${\kappa }_{\star }=\{\begin{array}{c}1-\mu ,\mu +\nu \ge 1,\\ 1-\mu -\nu ,\mu +\nu <1,\end{array}$

$K^{\ast }$ 的定义和(11)一致。

5. 数值实验

考虑以下形式的方程：

$t^{\frac{4}{3}}y\left(t\right)={\displaystyle {\int }_0^{0.5t}{\left(0.5t-\delta \right)}^{-\frac{1}{2}}}{\delta }^{\frac{5}{6}}y\left(\delta \right)\text{d}\delta +t^3-\frac{\Gamma \left(\frac{1}{2}\right)\Gamma \left(\frac{7}{2}\right)}{8\Gamma \left(4\right)}{t}^3,$ (18)

其中 $\mu =\frac{1}{2}$， $\nu =\frac{4}{3}$， $K\left(t,\delta \right)={\delta }^{\frac{5}{6}}$，精确解为 $y\left(t\right)=t^{\frac{5}{3}}$。由于该方程具有非光滑解，对此我们通过选取参数 $\lambda$ 的值，使得数值解更加接近解析解。首先分别选取 $\lambda =1,\frac{1}{2},\frac{1}{4},\frac{1}{5}$，比较参数 $\lambda$ 在不同取值下对方程求解的影响。其次选择权指标 $\alpha =\beta =-0.6$，分别计算 $L_{\infty }$ 和带权 $L_{{\omega }^{-0.6,-0.6,\lambda }}^2$ 范数下的误差。通过误差表1，表2，可以看出 $\lambda =1,N=24$ 时 $L_{\infty }$ 范数下误差为1.80e−05，远远大于 $\lambda$ 取值为分数的情况。从误差图1，图2可以看出 $\lambda =1$ 时误差衰减最缓慢，随 $\lambda$ 取值变小误差衰减率逐渐变大，当 $\lambda =\frac{1}{5}$ 时误差衰减最快，甚至在 $N=24$ 处数值解与精确解在 $L_{\infty }$ 范数下误差仅为2.40e−15，这表现了Müntz配置法具有更高精度，同时我们可以从误差图1，图2得出该方法具有指数收敛性，数值实验和理论分析高度吻合。综上所述，Müntz配置法在求解具有时滞项和非光滑解的第三类Volterra方程时具有较强的可行性和有效性。

Table 1. 4 ≤ N ≤ 24 , the L ∞ norm error

表1. $4\le N\le 24$， $L_{\infty }$ 范数下的误差

Table 2. 4 ≤ N ≤ 24 , the L ω − 0.6 , − 0.6 , λ 2 norm error

表2. $4\le N\le 24$， $L_{{\omega }^{-0.6,-0.6,\lambda }}^2$ 的范数下的误差

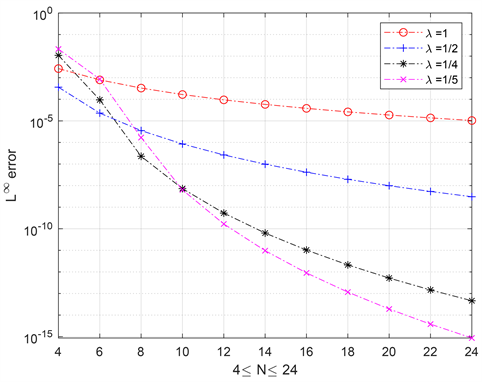
Figure 1. $4\le N\le 24$, the $L_{\infty }$ norm error

图1. $4\le N\le 24$， $L_{\infty }$ 范数下的误差

Figure 2. $4\le N\le 24$, the $L_{{\omega }^{-0.6,-0.6,\lambda }}^2$ norm error

图2. $4\le N\le 24$， $L_{{\omega }^{-0.6,-0.6,\lambda }}^2$ 的范数下的误差

6. 总结

我们采用具有谱精度的分数次Jacobi谱配点法求解了具有时滞项的第三类Volterra积分方程，讨论了在 $L_{\infty }$ 和加权 $L_{{\omega }^{\alpha ,\beta ,\lambda }}^2$ 范数下的误差估计。由于方程的解在原点附近具有奇异性，若采用经典的多项式配置法会降低全局收敛阶，因此采用分数次Lagrange多项式作为插值基函数得到数值解。最后证明了使用广义基函数能使得到的数值格式具有更好的误差精度。

基金项目

国家自然科学基金项目(11801127)；湖南省教育厅科研基金资助项目(20C0081)。

NOTES

^*通讯作者。