邻近的Hermite多项式灰色模型及其应用

Adjacent Hermite Polynomial Grey Model and Its Application

摘要: 针对传统灰色模型在建模上忽略对新数据的优先性以及缺乏微调数据的能力，本文引进了r阶邻近的累积生成算子，并且结合Hermite多项式的定义，优化了传统灰色模型的右端结构，构建了邻近的Hermite多项式灰色模型，即AHFGM(1,1)模型。基于中国一次电力及其他能源生产量的数据建立了预测模型，利用灰狼优化算法得到最优参数，与三个经典的灰色模型进行拟合和预测精确度分析，结果表明AHFGM(1,1)模型拥有更优的拟合和预测性能，以及较强的稳定性。最后利用建立的AHFGM(1,1)模型合理地预测了2021~2025年我国一次电力及其他能源生产量的变化趋势。

Abstract: In view of the fact that the traditional grey model ignores the priority of new data in modeling and lacks the ability to fine-tuneing the data, this paper introduces the r-order adjacent accumulative generator operator, and combines the definition of the Hermite polynomial to optimize the structure of the right end of the traditional grey model. The adjacent Hermite polynomial grey model, the AHFGM(1,1) model is constructed. Based on the data of primary power and other energy production in China, a prediction model is established, and the optimal parameters are obtained by using the grey wolf optimization algorithm. Fitting and prediction accuracy analysis with three classical grey models, the results show that the AHFGM(1,1) model has better fitting and prediction performance, as well as strong stability. Finally, the established AHFGM(1,1) model is used to reasonably predict the change trend of primary electricity and other energy production in my country from 2021 to 2025.

1. 引言

1982年邓聚龙教授首次提出了灰色系统理论 [1]，灰色预测模型能有效地处理小样本数据，并且运算速度快，因此得到了学者的广泛关注。经过多年的发展，灰色预测模型已经成功被运用到能源、工业、经济、科技等众多领域 [2]。

灰色累加生成算子是为了降低在建立灰色模型时原始数据的随机性，整数阶累加生成算子不能实现数据的微调，从而影响模型的预测精度。为了改进整数阶累加生成算子的不足，以及增强新数据在建模的优先性，吴利丰使用二项式定义了分数阶累加生成算子 [3]，Liu等基于邻近的累加原则提出了r阶邻近的累积生成算子 [4]。传统GM(1,1)作为灰色模型的基础拥有结构简单、操作简便等优点，但大量实验表明其预测结果不够理想。为了提高GM(1,1)模型的精度，主要从初始值优化、背景值优化、结构优化等方面进行改进 [5] [6]。崔杰为了增加GM(1,1)模型的适用性，引入bt项优化了GM(1,1)模型的右端结构，建立了NGM(1,1,k)模型 [7]。Chen等在GM(1,1)右端引入bt + c项，建立了NGM(1,1,k,c)模型 [8]。对于求解非线性规划问题，学者提出了大量的智能优化算法，如粒子群优化算法、鲸群优化算法、蚁群优化算法等，然而部分优化算法收敛性不强、运算速度较慢。其中灰狼优化算法已被证明能有效地搜索出非线性规划函数的最优解 [9]，并且拥有运算简便、收敛性强等优点被广泛应用于众多领域。

本文利用r阶邻近的累积生成算子，增强了新数据在建模时的优先性，通过引入Hermite多项式改变传统灰色模型右端的结构，建立适应性更强的邻近的Hermite多项式灰色模型。

2. 邻近的Hermite多项式灰色模型

2.1. r阶邻近的累积生成算子定义

定义1 [4]. 假设原始序列为 $X^{\left(0\right)}=\left\{x^{\left(0\right)}\left(1\right),x^{\left(0\right)}\left(2\right),\cdots ,x^{\left(0\right)}\left(n\right)\right\}$，其r阶邻近的累积生成算子 $X^{\left(r\right)}=\left\{x^{\left(r\right)}\left(1\right),x^{\left(r\right)}\left(2\right),\cdots ,x^{\left(r\right)}\left(n\right)\right\}$ 的表达式为

$x^{\left(r\right)}\left(k+1\right)=\frac{r-1}{r}{\displaystyle \underset{i=1}{\overset{k}{\sum }}{x}^{\left(0\right)}\left(k+1\right)}+\frac{1}{r}{x}^{\left(0\right)}\left(k+1\right),k=1,2,\cdots ,n-1$ (2.1-1)

2.2. AHPGM(1,1)的白化方程

定义2. 假设r阶邻近的累积生成算子 $X^{\left(r\right)}$ 满足定义1，那么AHPGM(1,1)的白化方程的定义为

$\frac{\text{d}{x}^{\left(r\right)}\left(t\right)}{\text{d}t}+a{x}^{\left(r\right)}\left(t\right)=b{H}_p\left(t\right)+u$ (2.2-1)

其中a，b，u为待定参数， $H_p\left(t\right)$ 是Hermite多项式，其表达式如下

$H_p\left(t\right)={\left(-1\right)}^p{\text{e}}^{t^2}\frac{{\text{d}}^p}{\text{d}{t}^p}{\text{e}}^{-t^2},p=0,1,2,\cdots$ (2.2-2)

p为Hermite多项式的阶数。在本文中，取 $p\in \left\{0,1,2,3,4,5\right\}$。

前六个物理学中的Hermite多项式如下

$\begin{array}{l}{H}_0\left(x\right)=1\\ H_1\left(x\right)=2x\\ H_2\left(x\right)=4x^2-2\\ H_3\left(x\right)=8x^3-12x\\ H_4\left(x\right)=16x^4-48x^2+12\\ H_5\left(x\right)=32x^5-160x^3+120x\end{array}$ (2.2-3)

2.3. AHPGM(1,1)的差分方程

对式子(2.2-1)的白化方程在 $\left[k-1,k\right]$ 上进行积分，得到差分方程

$x^{\left(r\right)}\left(k\right)-x^{\left(r\right)}\left(k-1\right)=\frac{b}{2}\left[H_p\left(k-1\right)+H_p\left(k\right)\right]-a{Z}^{\left(r\right)}\left(k\right)+u$ (2.3-1)

其中 $Z^{\left(r\right)}\left(k\right)$ 为 $X^{\left(r\right)}$ 的背景值序列，满足

$Z^{\left(r\right)}\left(k\right)=\frac{1}{2}\left(x^{\left(r\right)}\left(k\right)+x^{\left(r\right)}\left(k-1\right)\right)$ (2.3-2)

2.4. 参数估计

利用最小二乘估计得到AHPGM(1,1)模型的参数估计值

${\left[\begin{array}{ccc}a& b& u\end{array}\right]}^{\text{T}}={\left(B^{\text{T}}B\right)}^{\text{T}}{B}^{\text{T}}Y$ (2.4-1)

其中

$Y=\left[\begin{array}{c}{x}^{\left(r\right)}\left(2\right)-x^{\left(r\right)}\left(1\right)\\ x^{\left(r\right)}\left(3\right)-x^{\left(r\right)}\left(2\right)\\ ⋮\\ x^{\left(r\right)}\left(n\right)-x^{\left(r\right)}\left(n-1\right)\end{array}\right]$, $B=\left[\begin{array}{ccc}-Z^{\left(r\right)}\left(2\right)& \frac{1}{2}\left[H_p\left(1\right)+H_p\left(2\right)\right]& 1\\ -Z^{\left(r\right)}\left(3\right)& \frac{1}{2}\left[H_p\left(2\right)+H_p\left(3\right)\right]& 1\\ ⋮& ⋮& ⋮\\ -Z^{\left(r\right)}\left(n\right)& \frac{1}{2}\left[H_p\left(k-1\right)+H_p\left(k\right)\right]& 1\end{array}\right]$ (2.4-2)

2.5. AHPGM(1,1)模型求解

对于公式(2.2-1)，令 $f\left(t\right)=b{H}_p\left(t\right)+u$，那么AHPGM(1,1)的白化方程可写为

$\frac{\text{d}{x}^{\left(r\right)}\left(t\right)}{\text{d}t}+a{x}^{\left(r\right)}\left(t\right)=f\left(t\right)$ (2.5-1)

在方程(2.5-1)两端同时乘以 ${\text{e}}^{at}$，可得

${\text{e}}^{at}\frac{\text{d}{x}^{\left(r\right)}\left(t\right)}{\text{d}t}+a{\text{e}}^{at}{x}^{\left(r\right)}\left(t\right)={\text{e}}^{at}f\left(t\right)$ (2.5-2)

化简上述方程，得到

${\left(x\left(t\right){\text{e}}^{at}\right)}^{\prime }={\text{e}}^{at}{x}^{\prime }\left(t\right)+a{\text{e}}^{at}x\left(t\right)$ (2.5-3)

最终AHPGM(1,1)的白化方程可写为

$\frac{\text{d}{x}^{\left(r\right)}\left(t\right){\text{e}}^{at}}{\text{d}t}={\text{e}}^{at}f\left(t\right)$ (2.5-4)

对上述方程两端在[1, t]上进行积分

${\displaystyle {\int }_1^t\text{d}}{x}^{\left(r\right)}\left(t\right){\text{e}}^{a\tau }={\displaystyle {\int }_1^t{\text{e}}^{a\tau }f\left(t\right)\text{d}\tau }$ (2.5-5)

令 $x^{\left(r\right)}\left(1\right)=x^{\left(0\right)}\left(1\right)$，得到AHPGM(1,1)白化方程的解为

$x^{\left(r\right)}\left(t\right)=x^{\left(0\right)}\left(1\right){\text{e}}^{a\left(1-t\right)}+{\displaystyle {\int }_1^t{\text{e}}^{a\left(\tau -t\right)}\left(b{H}_p\left(t\right)+u\right)\text{d}\tau }$ (2.5-6)

应用梯形公式，白化方程的解可离散为

${\hat{x}}^{\left(r\right)}\left(t\right)=x^{\left(0\right)}\left(1\right){\text{e}}^{a\left(1-k\right)}+\frac{1}{2}{\displaystyle \underset{\tau =2}{\overset{k}{\sum }}\left[{\text{e}}^{a\left(\tau -k\right)}\left(b{H}_p\left(\tau \right)+u\right)+{\text{e}}^{a\left(\tau -k-1\right)}\left(b{H}_p\left(\tau -1\right)+u\right)\right]}$ (2.5-7)

结合式(2.5-7)的结果，得到预测值为

${\hat{x}}^{\left(0\right)}\left(k\right)=r\cdot {\hat{x}}^{\left(r\right)}\left(k+1\right)-\left(r-1\right){\displaystyle \underset{i=1}{\overset{k}{\sum }}{\hat{x}}^{\left(0\right)}\left(i\right)},k=2,3,\cdots ,n$ (2.5-8)

3. 构建AHPGM(1,1)的非线性规划函数

为了验证灰色模型的实用性，通常将平均绝对百分比误差MAPE作为模型的精确度的评价标准，其表达式为

$\text{MAPE}=\frac{1}{n}{\displaystyle \underset{k=1}{\overset{n}{\sum }}\left|\frac{{\hat{x}}^{\left(0\right)}\left(k\right)-x^{\left(0\right)}\left(k\right)}{x^{\left(0\right)}\left(k\right)}\right|\times 100\%}$ (3-1)

由于AHPGM(1,1)模型的建模步骤是在参数r和p已知的情况下完成的，因此在模型的实际应用中应先得到参数r和p的值。因此构建出AHPGM(1,1)模型的非线性规划函数参数r和p进行寻优。

假设AHPGM(1,1)建模的数据个数为S，其拟合平均相对误差为MAPEs。将建模的平均相对误差作为目标函数，AHPGM(1,1)的建模流程作为约束条件构建如下的非线性规划函数：

$\underset{r,p}{\text{min}}\text{MAPEs}\left(r,p\right)=\frac{1}{S}{\displaystyle \underset{k=1}{\overset{S}{\sum }}\left|\frac{{\hat{x}}^{\left(0\right)}\left(k\right)-x^{\left(0\right)}\left(k\right)}{x^{\left(0\right)}\left(k\right)}\right|\times 100\%}$

$\{\begin{array}{l}{x}^{\left(r\right)}\left(k+1\right)=\frac{r-1}{r}{\displaystyle \underset{i=1}{\overset{k}{\sum }}{x}^{\left(0\right)}\left(k+1\right)}+\frac{1}{r}{x}^{\left(0\right)}\left(k+1\right),k=1,2,\cdots ,S-1\\ {\left[\begin{array}{ccc}a& b& u\end{array}\right]}^{\text{T}}={\left(B^{\text{T}}B\right)}^{\text{T}}{B}^{\text{T}}Y\\ B=\left[\begin{array}{ccc}-Z^{\left(r\right)}\left(2\right)& \frac{1}{2}\left[H_p\left(1\right)+H_p\left(2\right)\right]& 1\\ -Z^{\left(r\right)}\left(3\right)& \frac{1}{2}\left[H_p\left(2\right)+H_p\left(3\right)\right]& 1\\ ⋮& ⋮& ⋮\\ -Z^{\left(r\right)}\left(n\right)& \frac{1}{2}\left[H_p\left(k-1\right)+H_p\left(k\right)\right]& 1\end{array}\right],Y=\left[\begin{array}{c}{x}^{\left(r\right)}\left(2\right)-x^{\left(r\right)}\left(1\right)\\ x^{\left(r\right)}\left(3\right)-x^{\left(r\right)}\left(2\right)\\ ⋮\\ x^{\left(r\right)}\left(n\right)-x^{\left(r\right)}\left(n-1\right)\end{array}\right]\\ {\hat{x}}^{\left(r\right)}\left(t\right)=x^{\left(0\right)}\left(1\right){\text{e}}^{a\left(1-k\right)}+\frac{1}{2}{\displaystyle \underset{\tau =2}{\overset{k}{\sum }}\left[{\text{e}}^{a\left(\tau -k\right)}\left(b{H}_p\left(\tau \right)+u\right)+{\text{e}}^{a\left(\tau -k-1\right)}\left(b{H}_p\left(\tau -1\right)+u\right)\right]}\\ {\hat{x}}^{\left(0\right)}\left(k\right)=r\cdot {\hat{x}}^{\left(r\right)}\left(k+1\right)-\left(r-1\right){\displaystyle \underset{i=1}{\overset{k}{\sum }}{\hat{x}}^{\left(0\right)}\left(i\right)},k=2,3,\cdots ,S\end{array}$ (3-2)

由于非线性规划函数计算的复杂度较高，因此借助智能优化算法对其进行搜索。其中灰狼优化算法模仿狼群等级划分、涉猎捕食等步骤，拥有运算速度快以及收敛性较强等优点，已经被应用于多个领域 [9]。本文利用灰狼优化算法对最优参数r和p进行搜索。

4. AHPGM(1,1)应用

随着化石资源不断枯竭以及环境日益恶化，全球开始寻求能源结构调整，持续推动发展清洁能源。面对世界能源发展的变革和国内的实际情况，中国大力发展清洁能源，优化能源生产的结构，其中一次电力能源及其他能源等清洁能源由于污染小、可利用率高等优点得到了世界各国的广泛的关注。中国致力于推动绿色发展，颁布了一系列政策，推动一次电力能源及其他能源的发展，因此合理的预测一次电力及其他能源生产量变化趋势能有效的为政策制定提前提供的理论参考，从而优化我国能源结构优化。

本文利用中国能源统计局收录的一次电力及其他能源生产量数据，将2010~2016年的数据作为训练集进行建模，2017~2020年的数据作为预测集进行模型预测能行分析，合理的分析各模型的性能。

4.1. AHPGM(1,1)建模步骤

1) 将2010~2016年的原始数据代入公式(3-2)构建出非线性规划函数，结合灰狼优化算法搜索出AHPGM(1,1)的最优参数r和p分别为0.80376和1。

2) 将原始序列和参数r代入公式(2.1-1)，得到r阶邻近的累积生成算子

$X^{\left(r\right)}=\left\{32461,32704.97,33017.09,27175.09,25002.79,17567.12,11284.40\right\}$

以及背景值序列

$Z^{\left(r\right)}=\left\{0,32582.98,32861.03,30096.09,26088.94,21284.95,14425.76\right\}$

3) 利用参数 $p=1$ 得到 $H_p\left(t\right)=2t$，将 $X^{\left(r\right)}$ 和 $Z^{\left(r\right)}$ 代入公式(2.4-2)构造出矩阵Y和矩阵B，结合最小二乘法 ${\left[\begin{array}{ccc}a& b& u\end{array}\right]}^{\text{T}}={\left(B^{\text{T}}B\right)}^{\text{T}}{B}^{\text{T}}Y$，可以计算出 $a=0.1907$， $b=-1098.6003$ 以及10259.1686，将估计值代入公式(2.5-7)和(2.5-8)中，最终得到2017-2020年的预测数据。

4.2. 模型分析

将建立的AHPGM(1,1)模型与经典灰色模型GM(1,1)、DGM(1,1)、Verhulst计算结果记录见表1，进行拟合和预测的精确度分析。

Table 1. Fitting and prediction results of each model in China’s primary power and other energy production

表1. 各模型在我国一次电力及其他能源生产量的拟合和预测结果

根据表1中的结果，可以看出四种不同模型在对训练集都表现出较好的拟合效果，并且MAPE值均小于3%，但是AHPGM(1,1)模型拟合MAPE值仅有1.2203%，展现出比GM(1,1)、DGM(1,1)、Verhulst更优的拟合能力。在对测试集的预测，AHPGM(1,1)模型的预测MAPE值远小于其余三种模型，拥有更佳的预测性能，因此AHPGM(1,1)模型在拟合和预测拥有更佳的性能和准确度。

同时，观察到表1中各模型每年的数据，和实际数据相比，AHPGM(1,1)模型每年的数据均要接近原始数据，表现出较高的稳定性。

4.3. AHPGM(1,1)模型预测分析

利用4.2节中AHPGM(1,1)模型的建模方法，对我国2021~2025年一次电力及其他能源生产量进行预测，并将预测的结果呈现在表2中。

Table 2. Predicted value of China’s primary power and other energy production from 2021 to 2025 by AHPGM(1,1) model

表2. AHPGM(1,1)模型预测2021~2025年我国一次电力及其他能源生产量的值

为了更直观的观察各模型拟合和预测结果与原始序列的变化趋势，绘制出拟合和预测趋势图见图1。

结合我国的能源结构不断调整的现实依据，不断加大对一次电力及其他能源的财政和政策支持，因此表2的预测数据和图1的趋势图符合现实要求。根据本文的预测结果，可以看出2021~2022年我国一次电力及其他能源的生产量继续保持稳定上升，因此为了保证我国能源结构优化，相关部门需要继续保持对一次电力及其他能源的生产量的政策扶持。

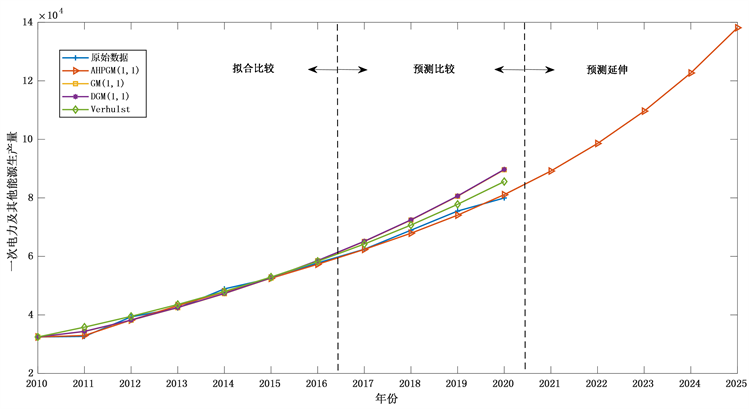
Figure 1. Fitting and prediction trend of each model and extension diagram of AHPGM(1,1) prediction

图1. 各模型拟合和预测趋势及AHPGM(1,1)预测延伸图

5. 结论

考虑到传统灰色模型未体现新数据的优先性，不能对原始数据进行微调以及右端结构适应性较弱等不足，本文根据r阶邻近的累积生成算子和Hermite多项式的定义，构建了邻近的Hermite多项式灰色模型，增强了灰色模型的种类。将中国一次电力及其他能源生产量2010~2016年的数据作为训练集建立模型，利用灰狼优化算法拟合最小平均相对误差得到最优参数，预测了2017~2020年的数据，与三个经典的灰色模型分别比较拟合和预测精确度，结果表明AHFGM(1,1)模型拥有更优的拟合和预测能力，并且运用AHFGM(1,1)模型做了预测延伸，合理地预测了2021~2025年我国一次电力及其他能源生产量的变化趋势。

根据本文AHFGM(1,1)模型的预测结果，说明我国一次电力及其他能源生产量将继续保持增长的趋势，但在2021年以及2022年增长率有所下降，结合我国的实际情况，本文建议为了不断优化能源的结构调整，减缓环境恶化的趋势，应当稳定加大对一次电力及其他能源的生产量，进一步释放化石资源的压力。