有遗失边的n维泡型图和修正泡型图在MM^*模型下的局部诊断度

The Local Diagnosability of n-Dimensional Bubble-Sort Graphs and Modified Bubble-Sort Graphs with Missing Edges under the MM^* Model

摘要: 故障诊断问题曾得到了广泛的研究，并且一些著名网络拓扑的可诊断性已被研究。n维泡型图MB_n和修正泡型图B_n有许多好的性质。n维修正泡型图是由n维泡型图添加n!/2条边得到的。在这篇文章中，我们首先研究了B_n在MM*模型下的诊断度，证明了B_n即使存在n-3条遗失边仍具有强局部诊断性，并且证明了是n-3最优值。然后，我们研究了MB_n在MM*模型下的诊断度，证明了MB_n即使存在n-2条遗失边仍具有强局部诊断性，并且证明了n-2是最优值。

Abstract: The problem of fault diagnosis has been discussed widely, and the diagnosability of some famous network topologies has been explorted. The n-dimensional bubble-sort graphs B_n and the n-dimensional modified bubble-sort graphs MB_n have many good properties. The n-dimensional modified bubble-sort graph MB_n is obtained by adding n!/2 edges to the n-dimensional bubble-sort graph B_n. In this paper, we firstly discuss the diagnosability of B_n, and show that it has the strong local diagnosability property even if there exist missing edges in it under the MM* model, and the result is optimal with respect to the number of missing edges. Then we discuss the diagnosability of MB_n, and show that it has the strong local diagnosability property even if there exist n-2 missing edges in it under the MM* model, and the result is optimal with respect to the number of missing edges.

1. 引言

许多系统都有一个网络作为底层拓扑，网络通常用一个图表示，其中顶点(节点)表示处理器，边(链接)表示处理器之间的通信链路。然而，在系统中处理器和通信链路故障是不可避免的。系统诊断就是识别出故障处理器的过程。在故障处理器的数量不超过t的情况下，如果所有的故障处理器可以被识别出来并且不被替换，我们就称这个系统G为t-可诊断的。一个系统G的诊断度 $t\left(G\right)$ 是使得G是t-可诊断的t的最大值 [1] [2] [3]。

对于一个t-可诊断系统，Dahbura和Masson [1] 提出了一种能够有效识别出故障处理器集的时间复杂度为 $O\left(n^{2.5}\right)$ 的诊断算法。在之前的研究中，研究者已经提出了许多系统诊断模型。Malek和Maeng [4] 首次提出了一个比较模型，称为MM模型，它允许处理器本身进行比较。在文献 [5] 中，Sengupta和Dahbura提出了MM*模型，它是MM模型的一个特例。在MM*模型中，每个节点必须测试其相邻节点的所有对。MM*模型被众所周知并广泛使用。

在文献 [6] 中，Hau和Tan首次提出了一种测量多重处理器系统的局部诊断度的概念。这种新的概念更关注每个处理器的局部可诊断性，而不是整个系统的可诊断性。如果只考虑全局故障或无故障状态，则可能会丢失系统的局部详细信息。在文献 [7] 中，Chiang和Tan提出了一种有用的局部结构称为扩展星结构，它可以保证节点的可诊断性，并在比较诊断模型(MM模型)下给出了确定局部可诊断性的充分条件。他们发现G的局部可诊断性与传统的G的可诊断性之间存在很强的关系。如果系统G的每个节点的局部可诊断性等于其在G中的度，则系统G具有强的局部可诊断性。根据这一概念，强局部可诊断性得到了广泛的研究。在文献 [8] 中，Chiang等证明了n维星图 $S_n\left(n\ge 4\right)$ 的诊断度是 $n-1$，且即使它存在高达 $n-3$ 条遗失边，仍保持强局部诊断性。Cheng等人又研究了置换树生成的Cayley图 [9] 和 $\left(n,k\right)$ 星图和2树生成的Cayley图 [10]。在2018年，Wang和Ma [11] 证明了交错群图 $A{G}_n$ 在MM*模型下即使存在 $2n-7$ 条遗失边，仍保持强局部诊断性。2019年，Wang等人 [12] 证明了n维泡型星图 $B{S}_n\left(n\ge 5\right)$ 在MM*模型下即使存在 $2n-5$ 条遗失边，仍保持强局部诊断性并且是最优的。2020年，Feng和Wang [13] 证明了n维轮图 $C{W}_n\left(n\ge 6\right)$ 在MM*模型下即使存在 $2n-4$ 条遗失边，仍保持强局部诊断性并且是最优的。2021年，Wang等人 [14] 首先证明了n维超立方体 $Q_n\left(n\ge 5\right)$ 在MM*模型下即使存在 $n-2$ 条遗失边，仍保持强局部诊断性并且是最优的，然后又证明了n维折叠超立方体 $F{Q}_n\left(n\ge 6\right)$ 在MM*模型下即使存在 $n-1$ 条遗失边，仍保持强局部诊断性并且是最优的。在这篇文章中，我们首先证明了n维泡型图 $B_n$ 的诊断度是 $n-1$，且在MM*模型下即使存在高达 $n-3$ 条遗失边仍保持强局部诊断性并且是最优的。然后，我们证明了n维修正泡型图 $M{B}_n$ 的诊断度是n，且在MM*模型下即使存在 $n-2$ 条遗失边仍保持强局部诊断性并且是最优的。

2. 基本概念

我们用一个无向简单图 $G=\left(V,E\right)$ 表示一个多重处理器系统，其中图G的顶点集 $V=V\left(G\right)$ 代表处理器，边集 $E=E\left(G\right)$ 代表处理器之间的通信链路。假设 $V^{\prime }$ 是V的一个非空子集，以 $V^{\prime }$ 为顶点集，以两端点均在 $V^{\prime }$ 中的边的全体为边集所组成的子图，称为G的由 $V^{\prime }$ 导出的子图，记为 $G\left[V^{\prime }\right]$， $G\left[V^{\prime }\right]$ 称为G的导出子图。图G中顶点v的度 $d_G\left(v\right)$ 是指图G中与v关联的边数。 $\delta \left(G\right)$ 表示图G中顶点的最小度。定义图G中任意一个顶点v的邻集是G中所有与v相邻的顶点的集合，记为 $N_G\left(v\right)$，简记为 $N\left(v\right)$。对于度、邻集等这些概念，在没有歧义产生时，我们通常省略图的下标。如果对于所有的 $v\notin V$ 都满足 $d\left(v\right)=k$，则这个图是k-正则的。G的一条途径是指一个有限非空序列 $P=v_0{e}_1{v}_1{e}_2{v}_2\cdots e_n{v}_n$，它的项交替地为顶点和边，使得对 $1\le i\le n$， $e_i$ 的端点是 $v_{i-1}$ 和 $v_i$，称P是从 $v_0$ 到 $v_n$ 的一条途径。 $v_0$ 到 $v_n$ 分别称为P的起点和终点，整数n称为P的长。若途径P的顶点 $v_0{v}_1\cdots v_n$ 互不相同，则P称为路。我们用 $P=\langle v_0{e}_1{v}_1{e}_2{v}_2\cdots e_n{v}_n\rangle$ 表示一条长为n的起点是 $v_0$，终点是 $v_n$ 的路。x和y之间最短路径的长度称为x和y之间的距离，用 $d_G\left(x,y\right)$ 表示。如果把G中的点集任意划分为两个非空子集X和Y，总存在一条边满足其中一个端点在X中，另一个端点在Y中，那么G是连通的。一个图G的连通度 $\kappa \left(G\right)$ 是把图G变成一个不连通图或平凡图所需移除的点的最小数量。一个图是二部图(偶图)，如果它的顶点集可以划分为两个(非空)子集X和Y，使得每条边都有一个端点在X中，另一个端点在Y中；这样一种分类 $\left(X,Y\right)$ 称为图的一个二分类，X和Y是它的两个部分。我们用 $G=\left(V,Y;E\right)$ 定义简单二部图G。如果X中的每个顶点都与Y中的每个顶点相连，那么图 $G=\left(V,Y;E\right)$ 称作完全二部图；若 $\left|X\right|=n$， $\left|Y\right|=m$，则图G记为 $K_{n,m}$。图G中最短圈的长度称为G的围长。如果图G中任意一对顶点u和v存在一个自同构 $\phi$，使得 $\phi \left(u\right)=v$，则图G的自同构群是传递的。在这种情况下，G被称为是顶点传递的。文中其它未定义而直接使用的符号和术语参见文献 [15]。

3. MM*模型

MM模型最早是由Malek和Maeng [4] 提出来的。在MM模型中，一个处理器发送同样的任务给一对不同的邻点，然后比较它们的反应结果。一个系统 $G=\left(V\left(G\right),E\left(G\right)\right)$ 的比较方案被模型化为一个多重图，用 $M=\left(V\left(G\right),L\right)$ 表示，其中L是被标记的边集。一条被标记的边 ${\left(u,v\right)}_w\in L$ 代表用一个顶点w去比较两个相邻顶点u和v，这意味着 $uw,vw\in E\left(G\right)$。如果节点w是非故障的(故障的)，那么测试结果是可靠的(不可靠的)。如果 $u,v\in F$ 且 $w\in V\left(G\right)\backslash F$，则 ${\left(u,v\right)}_w\to 1$。如果 $u\in F$ 且 $v,w\in V\left(G\right)\backslash F$，则 ${\left(u,v\right)}_w\to 1$。如果 $v\in F$ 且 $u,w\in V\left(G\right)\backslash F$，则 ${\left(u,v\right)}_w\to 1$。如果 $u,v,w\in V\left(G\right)\backslash F$，则 ${\left(u,v\right)}_w\to 0$。 $M=\left(V\left(G\right),L\right)$ 中所有比较结果的集合称为诊断的症候，用 $\sigma$ 表示。如果比较 ${\left(u,v\right)}_w$ 的结果不一致，则 $\sigma \left({\left(u,v\right)}_w\right)=1$ ；否则， $\sigma \left({\left(u,v\right)}_w\right)=0$。因此，一个症候L是从到 $\left\{0,1\right\}$ 的一个函数。MM*中每个节点必须测试其任意一对相邻节点。即如果 $uw,vw\in E\left(G\right)$，则 ${\left(u,v\right)}_w\in L$。在系统中，所有故障处理器的集合叫做一个故障集，它可以是 $V\left(G\right)$ 的任意一个子集。在MM*模型下，对于一个给定的症候 $\sigma$，如果对任意的 ${\left(u,v\right)}_w\in L$ 满足 $w\in V\backslash F$， $\sigma \left({\left(u,v\right)}_w\right)=1$ 当且仅当 $u,v\in F$ 或 $u\in F$ 或 $v\in F$，则我们称故障子集 $F\subseteq V\left(G\right)$ 和 $\sigma$ 是一致的。我们用 $\sigma \left(F\right)$ 表示和F一致的所有症候的集合。设 $F_1$ 和 $F_2$ 是 $V\left(G\right)$ 中两个不同的子集。如果 $\sigma \left(F_1\right)\cap \sigma \left(F_2\right)=\varnothing$，则 $\left(F_1,F_2\right)$ 是可区分对；否则， $\left(F_1,F_2\right)$ 是不可区分对。

引理3.1 [16] 一个系统 $G=\left(V,E\right)$ 是t-可诊断的，当且仅当对于 $\left|F_1\right|\le t$， $\left|F_2\right|\le t$ 的每一对不同的顶点集 $\left(F_1,F_2\right)$， $\left(F_1,F_2\right)$ 是一个可区分对。

4. n维泡型图B_n

泡型图是互连网络的一种著名的拓扑结构，本节将介绍它的定义和一些有用的性质。

在置换 $\left(\begin{array}{llll}1\hfill & 2\hfill & \cdots \hfill & n\hfill \\ p_1\hfill & p_2\hfill & \cdots \hfill & p_n\hfill \end{array}\right)$ 中， $i\to p_i$，为了方便用 $p_1{p}_2\cdots p_n$ 表示置换 $\left(\begin{array}{llll}1\hfill & 2\hfill & \cdots \hfill & n\hfill \\ p_1\hfill & p_2\hfill & \cdots \hfill & p_n\hfill \end{array}\right)$。在本文中，置换有时也用不相交的轮换的乘积表示 [17]。例如， $\left(\begin{array}{lll}1\hfill & 2\hfill & 3\hfill \\ 2\hfill & 3\hfill & 1\hfill \end{array}\right)=\left(123\right)$。特别地， $\left(\begin{array}{llll}1\hfill & 2\hfill & \cdots \hfill & n\hfill \\ 1\hfill & 2\hfill & \cdots \hfill & n\hfill \end{array}\right)=\left(1\right)$。两个置换的乘积 $\sigma \tau$ 是先作用于 $\tau$ 后作用于 $\sigma$ 的复合函数，例如， $\left(12\right)\left(13\right)=\left(132\right)$。对于这里未定义的术语和符号，我们遵循 [17]。

设 $\left[n\right]=\{1,2,\cdots ,n\}$，设 $S_n$ 为 $\left[n\right]$ 上包含所有置换 $p_1{p}_2\cdots p_n$ 的对称群。n维泡型图 $B_n$ [18] 是顶点集为 $V\left(B_n\right)=S_n$ 的图，当且仅当 $u=v\left(i,i+1\right)\left(1\le i\le n-1\right)$ 时，其中两个顶点u和v相邻。从定义很容易看出 $B_n$ 是一个 $\left(n-1\right)$ -正则图， $\left|V\left(B_n\right)\right|=n!$， $\left|E\left(B_n\right)\right|=\left(n-1\right)n!/2$。图 $B_2$， $B_3$ 和 $B_4$ 见图1。我们可以将 $B_n$ 分解为n个子图 $B_n^1$， $B_n^2$， $\cdots$， $B_n^n$，其中每个顶点 $u=x_1{x}_2\cdots x_n\in V\left(B_n\right)$ 的最后一个位置 $x_n$ 为一个固定的整数i，其中 $i\in \left[n\right]$。很容易证明 $B_n^i$ 同构于 $B_{n-1}$。设 $v\in V\left(B_n\right)$，那么 $v\left(n-1,n\right)$ 被称为v的外部邻域。

注意， $B_n$ 是一个特殊的Cayley图。 $B_n$ 有以下有用的性质：

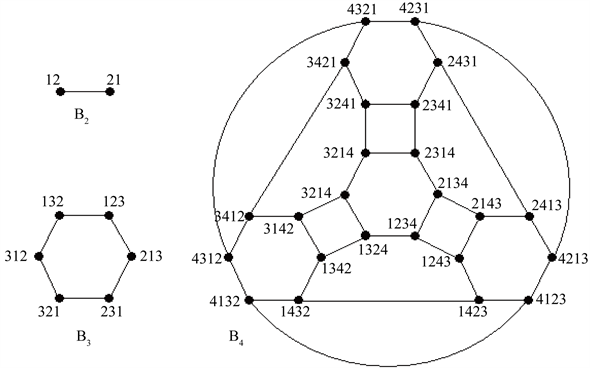
Figure 1. The bubble-sort graphs $B_2$， $B_3$ and $B_4$

图1. 泡型图 $B_2$， $B_3$ 和 $B_4$

命题4.1 [19] 对任意的正整数 $n\ge 2$， $B_n$ 是 $\left(n-1\right)$ -正则的并且是顶点传递的。

命题4.2 [20] 对任意的正整数 $n\ge 2$， $B_n$ 是二部图。

命题4.3 [21] 对任意的正整数 $n\ge 3$， $B_n$ 的围长为4。

命题4.4 [20] 设 $B_n$ 是泡型图，那么 $\kappa \left(B_n\right)=n-1$。

5. n维修正泡型图MB_n

修正泡型图是一种著名的互联网络拓扑结构，本节将介绍它的定义和一些有用的性质。

设 $\Gamma$ 为有限群，S是 $\Gamma$ 的生成集，其中S不含单位元。有向凯莱图 $Cay\left(\Gamma ,S\right)$ 定义如下：它的点集是 $\Gamma$，边集是 $\{\left(g,gs\right):g\in \Gamma ,s\in S\}$。如果对任意的 $s\in S$ 有 $s^{-1}\in S$，我们说这个凯莱图是无向凯莱图。本文中的凯莱图均为无向凯莱图。

设 $\left[n\right]=\{1,2,\cdots ,n\}$。在本文中，我们考虑凯莱图 $Cay\left(S_n,H\right)$，其中 $S_n$ 是 $\left[n\right]$ 上的对称群，H是 $S_n$ 转置的集合。设 $G\left(H\right)$ 是n个顶点上的图，且在 $G\left(H\right)$ 中存在一条边ij当且仅当置换 $\left(ij\right)\in H$。图 $G\left(H\right)$ 称为 $Cay\left(S_n,H\right)$ 的置换生成图。当 $G\left(H\right)$ 是一棵树时，用 ${\Gamma }_n$ 表示。特别地，当 $G\left(H\right)$ 是一条路时， $Cay\left(S_n,H\right)$ 是n维泡型图 $B_n$ [18]。当 $G\left(H\right)$ 为一个圈时， $Cay\left(S_n,H\right)$ 为n维修正泡型图 $M{B}_n$ [22]。n维修正泡型图 $M{B}_n$ 是顶点集为 $V\left(B_n\right)=S_n$ 的图，当且仅当 $v=u\left(i,i+1\right)\left(1\le i\le n-1\right)$ 或 $v=u\left(1n\right)$ 时，其中两个顶点u和v相邻。设 $G\left(H\right)$ 是为 $\left(123\cdots n1\right)$ 的圈。如果我们从圈 $G\left(H\right)$ 中删除顶点n，则会得到一条有 $\left(n-1\right)$ 个顶点的路，并且 $G\left(H\right)-\left\{n\right\}$ 中的所有边都是 $S_{n-1}$ 的生成集。我们可以将 $M{B}_n$ 分解为n个子图 $M{B}_n^1$， $M{B}_n^2$， $\cdots$， $M{B}_n^n$，其中每个顶点 $u=u_1{u}_2\cdots u_n\in V\left(M{B}_n\right)$ 的最后一个位置 $u_n$ 为一个固定的整数i，其中 $i\in \left[n\right]$。显然， $M{B}_n^i$ 同构于 $B_{n-1}$，其中 $B_{n-1}$ 是一个 $\left(n-1\right)$ 维的泡型图。从定义很容易看出修正泡型图 $M{B}_n$ 是一个n-正则图， $\left|V\left(M{B}_n\right)\right|=n!$， $\left|E\left(M{B}_n\right)\right|=n\cdot n!/2$。图 $M{B}_3$ 和 $M{B}_4$ 见图2。设 $v\in V\left(M{B}_n\right)$，则 $v\left(n-1,n\right)$ 和 $v\left(1n\right)$ 是v的两个外部邻域。

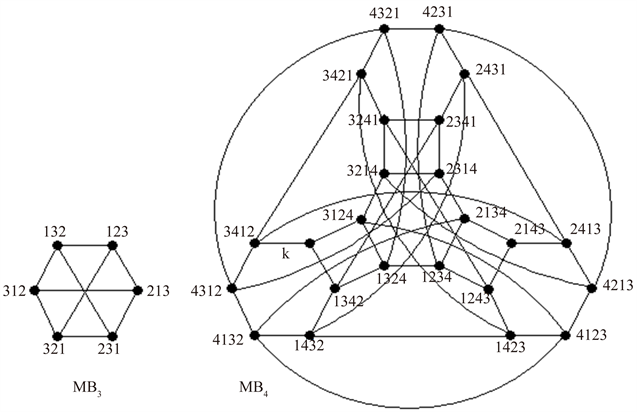
Figure 2. The modified bubble-sort graphs $M{B}_3$ 和 $M{B}_4$

图2. 修正泡型图 $M{B}_3$ 和 $M{B}_4$

注意， $M{B}_n$ 是一个特殊的Cayley图。 $M{B}_n$ 有以下有用的性质：

命题5.1 [22] 对任意的正整数 $n\ge 3$， $M{B}_n$ 是顶点传递和二部的。

命题5.2 [23] 对任意的正整数 $n\ge 3$， $M{B}_n$ 的围长为4。

命题5.3 [24] 设 $M{B}_n$ 是修正泡型图，那么 $\kappa \left(M{B}_n\right)=n$。

6. 局部诊断度

对于一个图 $G=\left(V,E\right)$，设 $F_1$ 和 $F_2$ 是V的两个不同子集，并设对称差 $F_1\Delta F_2=\left(F_1\backslash F_2\right)\cup \left(F_2\backslash F_1\right)$。

引理6.1 [8] 一个系统 $G=\left(V,E\right)$ 在顶点x处是局部t-可诊断的，如果给定一个测试症候 ${\sigma }_F$，它是由系统在一组包含x的故障顶点集F的情况下产生的， $\left|F\right|\le t$，故障顶点集 $F^{\prime }$ 的每一个集合与 ${\sigma }_F$ 一致，且 $\left|F^{\prime }\right|\le t$ 必须包含顶点x。

引理6.2 [7] 一个系统 $G=\left(V,E\right)$ 在顶点x是局部t-可诊断的，如果 $x\in F_1△F_2$ 且对于V中的每一对不同的故障子集 $F_1$ 和 $F_2$ 是可区分的，其中 $\left|F_1\right|\le t$ 且 $\left|F_2\right|\le t$。

引理6.1和引理6.2是等价的。

引理 6.3 [8] 一个系统 $G=\left(V,E\right)$ 是t-可诊断的当且仅当G中的每个顶点都是局部t-可诊断的。G的可诊断性 $t\left(G\right)$ 是使G具有t-可诊断性的t的最大值。

定义6.1 [8] 一个系统 $G=\left(V,E\right)$ 中，G中x点是局部t-可诊断的t的最大值被定义为点x的局部诊断度 $t_l\left(x\right)$，即 $t_l\left(x\right)=\max \left\{t:G在x�是局部t\text{-}可��的\right\}$。

引理6.4 [8] 一个系统 $G=\left(V,E\right)$ 的诊断度 $t\left(G\right)$ 等于G中每个点的局部诊断度的最小值，即 $t\left(G\right)=\min \left\{t_l\left(x\right):�于所有的x\in V\left(G\right)\right\}$。

定义6.2 [8] 设x是一个图 $G=\left(V,E\right)$ 中的一个点。若 $d_G\left(x\right)\ge n$，我们定义一个扩展星图 $ES\left(x;n\right)$，其中 $d_{ES\left(x;n\right)}\left(x\right)=n$，点集 $V\left(ES\left(x;n\right)\right)=\left\{x\right\}\cup \left\{v_{ij}:1,2,\cdots ,n,j=1,2,3,4\right\}$，边集 $E\left(ES\left(x;n\right)\right)=\left\{\left(x,v_{k1}\right),\left(v_{k2},v_{k2}\right),\left(v_{k2},v_{k3}\right),\left(v_{k3},v_{k4}\right):k=1,2,\cdots ,n\right\}$。

注意x被称为扩展星图 $ES\left(x;n\right)$ 的根。

引理6.5 [8] 设x是系统 $G=\left(V,E\right)$ 中的一个点且 $d_G\left(x\right)=n$。如果点x在G中存在一个扩展星图 $ES\left(x;n\right)$，则x的局部诊断度是n。

引理6.6 [25] 设G是系统的图表示，那么在MM*模型下可诊断度 $t\left(G\right)\le \delta \left(G\right)$。

引理6.7 [8] 设x是图 $G=\left(V,E\right)$ 中的一个顶点。如果x的局部诊断度等于它在G中的度，即 $t_l\left(x\right)=d_G\left(x\right)$，则这个点x具有强局部诊断性。

引理 6.8 [8] 设 $G=\left(V,E\right)$ 是一个图。如果G中每个点的局部诊断度都等于它在G中的度，即对于所有的 $x\in V\left(G\right)$ 都有 $t_l\left(x\right)=d_G\left(x\right)$，则G有强局部诊断性。

引理6.9 [1] [5] 一个系统 $G=\left(V,E\right)$ 在MM*模型下t-可诊断的，当且仅当对于V的每一对不同的故障子集 $F_1$ 和 $F_2$，其中 $\left|F_1\right|\le t$， $\left|F_2\right|\le t$，满足下列条件之一：

1) 有两个顶点 $u,w\in V\left(G\right)\backslash \left(F_1\cup F_2\right)$，有一个顶点 $v\in F_1\Delta F_2$，使得 $uw\in E\left(G\right)$， $vw\in E\left(G\right)$。

2) 有两个顶点 $u,v\in F_1\backslash F_2$，有一个顶点 $w\in V\left(G\right)\backslash \left(F_1\cup F_2\right)$，使得 $uw\in E\left(G\right)$， $vw\in E\left(G\right)$。

3) 有两个顶点 $u,v\in F_2\backslash F_1$，有一个顶点 $w\in V\left(G\right)\backslash \left(F_1\cup F_2\right)$，使得 $uw\in E\left(G\right)$， $vw\in E\left(G\right)$。

7. n维泡型图B_n的诊断度

引理 7.1 令x是n维泡型图 $B_n\left(n\ge 5\right)$ 中的任意一个顶点，在 $B_n$ 中存在一个以x为根的扩展星图 $ES\left(x;n-1\right)$。

证明 我们需找到一个扩展星图 $ES\left(x;n-1\right)$ 作为n维泡型图 $B_n$ 在给定顶点x处的子图。由命题4.1， $B_n$ 是顶点传递的。不失一般性，令 $x=12\cdots n=\left(1\right)$ 作为 $ES\left(\left(1\right);n-1\right)$ 的一个根。当 $n=5$ 时，在 $B_5$ 中存在一个以 $\left(1\right)$ 为根的扩展星图 $ES\left(\left(1\right);4\right)$ (见图3)。由图3可知， $ES\left(\left(1\right);4\right)$ 中的每个顶点都是不同的。

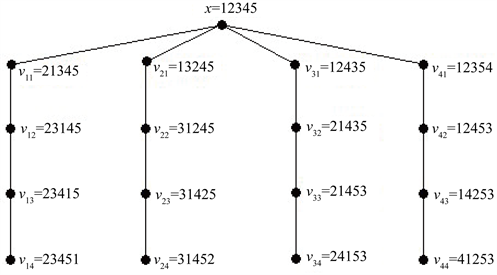
Figure 3. The first extended star $ES\left(\left(1\right);4\right)$ of $B_n$

图3. $B_n$ 的第一个扩展星图 $ES\left(\left(1\right);4\right)$

假设这个结论对于 $B_{n-1}\left(n\ge 6\right)$ 成立，即在 $B_{n-1}$ 中存在一个扩展星图 $ES\left(\left(1\right);n-2\right)$。现在我们证明这个结论对于 $B_n\left(n\ge 6\right)$ 成立，即在 $B_n$ 中存在一个扩展星图 $ES\left(\left(1\right);n-1\right)$。我们可以将 $B_n$ 分解为n个不相同的 $\left(n-1\right)$ 维泡型图 $B_n^1$， $B_n^2$， $\cdots$， $B_n^n$，它们分别由 $B_n$ 中顶点最右位是 $i\left(1\le i\le n\right)$ 的顶点导出的子图。注意到当 $i=1,2,\cdots ,n$ 时， $B_n^i$ 同构于 $B_{n-1}$。由归纳假设，在 $B_n^n$ 中存在一个扩展星图 $ES\left(\left(1\right);n-2\right)$。注意 $\left(1\right)$ 有一个外部邻点 $\left(n-1,n\right)$，且 $\left(n-1,n\right)\in V\left(B_n^{n-1}\right)$。在 $B_n^{n-1}$ 中存在一条三长路 $P_l=\langle \left(n-1,n\right),\left(12\right)\left(n-1,n\right),\left(123\right)\left(n-1,n\right),\left(1234\right)\left(n-1,n\right)\rangle$。连接 $P_l$ 到x，然后将它与 $ES\left(\left(1\right);n-2\right)$ 相结合。于是，我们可以在 $B_n$ 中找到一个以 $\left(1\right)$ 为根的扩展星图 $ES\left(\left(1\right);n-1\right)$，即在 $B_n$ 中存在一个以x为根的扩展星图 $ES\left(x;n-1\right)$。

定理 7.1 设 $B_n\left(n\ge 5\right)$ 是一个n维泡型图，则 $B_n$ 的诊断度为 $n-1$，即 $t\left(B_n\right)=n-1$ 并且 $B_n$ 有强局部可诊断性。

证明 由引理6.5和7.1， $B_n$ 中每个顶点x的局部诊断度都是 $n-1$。由引理6.3， $B_n$ 的诊断度为 $n-1$，即 $t\left(B_n\right)=n-1$。由于 $B_n$ 中每个顶点x的度是 $n-1$，那么 $B_n$ 中每个顶点的局部可诊断度等于其在 $B_n$ 中的度。由引理6.7， $B_n$ 中的每个顶点x具有强局部可诊断性。由引理6.8， $B_n$ 具有强局部可诊断性。

引理7.2 设 $F_e$ 是 $B_n\left(n\ge 5\right)$ 中任意的遗失边集且 $\left|F_e\right|\le n-3$。x是 $B_n\left(n\ge 5\right)$ 中的任意一个顶点，在 $B_n-F_e$ 中存在一个以x为根的扩展星图 $ES\left(x;d_{B_n-F_e}\left(x\right)\right)$，其中 $x\in V\left(B_n\right)$。

证明 我们通过归纳n来证明这个引理。由命题4.1， $B_n$ 是顶点传递的。不失一般性，令 $x=12\cdots n=\left(1\right)$ 作为扩展星图 $ES\left(x;d_{B_n-F_e}\left(x\right)\right)$ 的根。当 $n=5$ 时，我们可以在 $B_5$ 中点 $\left(1\right)$ 处找到三个扩展星图 $ES\left(\left(1\right);4\right)$。显然，这些图中除了与 $\left(1\right)$ 相关联的边外，其它所有边都不相同。第一个扩展星图与图3相同，其余两个扩展星图分别在图4和图5中展示。

注意 $\left|F_e\right|\le n-3=5-3=2$，则我们只需考虑遗失边数为2。设 $t\left(0\le t\le 2\right)$ 是与x相关联的遗失边数，则 $2-t$ 为与x不相关联的遗失边数。如果 $t=0$，则 $2-t=2$，我们得到有两条遗失边与x不相关联。因为我们已经找到了三个扩展星图 $ES\left(\left(1\right);4\right)$，所以我们可以在这三个扩展星图中选择一个不包含任何遗失边的扩展星图 $ES\left(\left(1\right);4\right)$。如果 $t=1$，则 $2-t=1$。同样，我们可以找到一个扩展星图 $ES\left(\left(1\right);3\right)$。如果 $t=2$，则 $2-t=0$。同样，我们可以找到一个扩展星图 $ES\left(\left(1\right);2\right)$。因此，我们可以找到一个有两条遗失边的扩展星图 $ES\left(\left(1\right);4-t\right)$。综上所述，在 $B_5-F_e$ 中存在一个扩展星图 $ES\left(x;d_{B_5-F_e}\left(x\right)\right)$，其中 $\left|F_e\right|\le 2$。

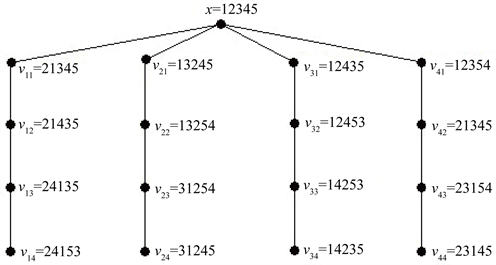
Figure 4. The second extended star $ES\left(\left(1\right);4\right)$ of $B_n$

图4. $B_n$ 的第二个扩展星图 $ES\left(\left(1\right);4\right)$

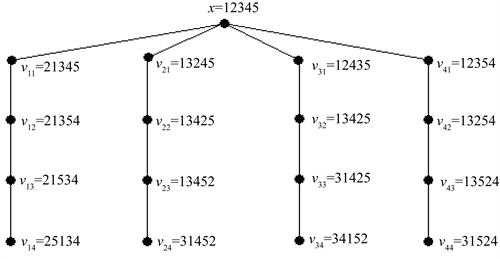
Figure 5. The third extended star $ES\left(\left(1\right);4\right)$ of $B_n$

图5. $B_n$ 的第三个扩展星图 $ES\left(\left(1\right);4\right)$

假设该结论对于 $B_{n-1}\left(n\ge 6\right)$ 成立，即在 $B_{n-1}-F_e$ 中存在一个扩展星图 $ES\left(x;d_{B_{n-1}-F_e}\left(x\right)\right)$。现在我们证明该结论对于 $B_n\left(n\ge 6\right)$ 成立，即在 $B_n-F_e$ 中存在一个扩展星图 $ES\left(x;d_{B_n-F_e}\left(x\right)\right)$。设 $B_n^i$ 是由 $B_n$ 中顶点最后一个位置 $i\left(1\le i\le n\right)$ 诱导的子图，则 $B_n^i$ 同构于 $B_{n-1}$。设 $x=12\cdots n=\left(1\right)$。注意 $\left(1\right)$ 在 $B_n^n$ 中。根据泡型图 $B_n$ 的定义， $\left(1\right)$ 有一个外部邻点 $\left(n-1,n\right)$， $\left(n-1,n\right)\in V\left(B_n^{n-1}\right)$。设 $y=\left(n-1,n\right)$， $F_e^i=F_e\cap E\left(B_n^i\right)\left(1\le i\le n\right)$。注意 $\left|F_e\right|\le 3$，那么 $\left|F_e^i\right|\le n-3\left(1\le i\le n\right)$。为了证明这个引理，我们首先需要在 $B_n^n-F_e^n$ 中找到一个扩展星图 $ES\left(x;d_{B_n^n-F_e^n}\left(x\right)\right)$，然后在 $B_n^{n-1}$ 中找到一条三长路 $P_y$。我们连接 $P_y$ 到x，然后将它与 $ES\left(x;d_{B_n^n-F_e^n}\left(x\right)\right)$ 相结合。于是，我们可以在 $B_n-F_e$ 中找到一个扩展星图 $ES\left(x;d_{B_n-F_e}\left(x\right)\right)$。接下来我们从以下情形展开讨论。

情形1 $\left|F_e^n\right|\le n-4$。

由归纳假设，在 $B_n^n-F_e^n$ 中存在一个扩展星图 $ES\left(x;d_{B_n^n-F_e^n}\left(x\right)\right)$。为了方便，我们假设 $A=ES\left(x;d_{B_n^n-F_e^n}\left(x\right)\right)$。如果 $xy\in F_e$，则不需要通过 $xy$ 扩展A。现在假设 $xy\notin F_e$。由命题4.4， $\kappa \left(B_n^1\right)=n-2$。因为 $\kappa \left(B_n^1\right)=n-2>n-3\ge \left|F_e^1\right|$，所以 $B_n^1-F_e^1$ 是连通的。当 $n\ge 6$ 时， $\left|V\left(B_n^1-F_e^1\right)\right|=\left|V\left(B_n^1\right)\right|=\left(n-1\right)!\ge 120$，因此在 $B_n^1-F_e^1$ 中存在一条三长路 $P_y$。所以 $P_y\cup \left\{xy\right\}$ 是 $B_n-F_e$ 中一条四长路。我们再把它与A相结合就得到一个扩展星图 $ES\left(x;d_{B_n-F_e}\left(x\right)\right)$。

情形2 $\left|F_e^n\right|=n-3$。

注意 $y=\left(n-1,n\right)$， $y=\left(n-1,n\right)\in V\left(B_n^{n-1}\right)$，则我们可以找到两条不同的以y为起点的三长路。 $P_y^1=\langle \left(n-1,n\right),\left(n-2,n,n-1\right),\left(12\right)\left(n-2,n,n-1\right),\left(12\right)\left(34\right)\left(n-2,n,n-1\right)\rangle$， $P_y^2=\langle \left(n-1,n\right),\left(23\right)\left(n-1,n\right),\left(23\right)\left(45\right)\left(n-1,n\right),\left(23\right)\left(456\right)\left(n-1,n\right)\rangle$。显然， $P_y^1$ 和 $P_y^2$ 除了顶点y之外没有公共顶点。因为 $\left|F_e\right|\le n-3$ 且 $\left|F_e^n\right|=n-3$，所以在 $V\left(B_n^{n-1}\right)$ 中不存在遗失边 $F_e$。于是，我们可以从 $P_y^1$ 和 $P_y^2$ 中选择一条不包含遗失边的三长路 $P_y$。假设 $f\in F_e^n$ 且 ${F^{\prime }}_e=F_e^n\backslash \left\{f\right\}$。此时 $\left|{F^{\prime }}_e\right|=n-4$。由归纳假设，在 $B_n^n-{F^{\prime }}_e$

中存在一个扩展星图 $ES\left(x;d_{B_n^n-{F^{\prime }}_e}\left(x\right)\right)$。假设 $f\notin E\left(A\right)$，我们在 $B_n^n-F_e^n$ 中得到一个以x为根的扩展星图

$ES\left(x;d_{B_n^n-F_e^n}\left(x\right)\right)$。假设 $f\in E\left(A\right)$。我们考虑如下情形。

情形2.1 f与x相关联。

我们可以在A中删除包含f的路得到 $ES\left(x;d_{B_n^n-F_e^n}\left(x\right)\right)$。然后从 $P_y^1$ 和 $P_y^2$ 中选择一条不包含遗失边的三长路 $P_y$，连接 $P_y$ 到x，然后把它与 $ES\left(x;d_{B_n^n-F_e^n}\left(x\right)\right)$ 相结合。于是，我们可以在 $B_n-F_e$ 中找到一个以x为根的扩展星图 $ES\left(x;d_{B_n-F_e}\left(x\right)\right)$。

情形2.2 f与x不相关联。

若m与x相邻， $P_m$ 是以m为起点且包含f的三长路。注意到， $N_{B_n}\left(\left(1\right)\right)=\left\{\left(i,i+1\right)|i=1,2,\cdots ,n-1\right\}$ 且 $m\in V\left(B_n^n\right)$。假设 $m=\left(i,i+1\right)\left(1\le i\le n-2\right)$。由n维泡型图的定义，m只有一个外部邻点 $\left(i,i+1\right)\left(n-1,n\right)\left(1\le i\le n\right)$ 或者 $\left(n-2,n-1,n\right)\left(i=n-2\right)$，因此， $\left(i,i+1\right)\left(n-1,n\right)\in V\left(B_n^{n-1}\right)$ 或者 $\left(n-2,n-1,n\right)\in V\left(B_n^{n-2}\right)$。我们只需要找到一条以 $m^{\prime }$ 为起点的二长路。不失一般性，假设 $m^{\prime }=\left(i,i+1\right)\left(n-1,n\right)\in V\left(B_n^{n-1}\right)\left(1\le i\le n-3\right)$。

情形2.2.1 $m^{\prime }=\left(i,i+1\right)\left(n-1,n\right)\in V\left(B_n^{n-1}\right)$， $1\le i\le n-3$。

注意 $P_y^1=\langle \left(n-1,n\right),\left(n-2,n,n-1\right),\left(12\right)\left(n-2,n,n-1\right),\left(12\right)\left(34\right)\left(n-2,n,n-1\right)\rangle$。当 $n\ge 6$ 时，存在两个正整数j，k，使得 $j,k\ne i$， $j\ne k$ 且 $1\le j,k\le n-3$。于是我们可以找到一条从 $m^{\prime }$ 开始的二长路，即 $P_{m^{\prime }}=\langle \left(i,i+1\right)\left(n-1,n\right),\left(i,i+1\right)\left(n-1,n\right)\left(j,j+1\right),\left(i,i+1\right)\left(n-1,n\right)\left(j,j+1\right)\left(k,k+1\right)\rangle$。很容易发现 $V\left(P_{m^{\prime }}\right)\cap V\left(P_y^1\right)=\varnothing$。将 $m^{\prime }$ 连接到m，这样我们就得到一条以m为起点的三长路 $P_m$。连接 $P_m$ 和 $P_y$ 到x，然后将它们与 $ES\left(x;d_{B_n^n-F_e^n}\left(x\right)\right)$ 相结合。于是，我们可以在 $B_n-F_e$ 中找到一个以x为根的扩展星图 $ES\left(x;d_{B_n-F_e}\left(x\right)\right)$。

定理7.2 设 $F_e$ 是n维泡型图 $B_n$ 中的任意边子集且 $\left|F_e\right|\le n-3$。对 $B_n$ 中的每个点x， $B_n-F_e$ 具有强局部诊断性，其中 $F_e$ 的个数是最优的。

证明 由引理6.5和7.2，当 $n\ge 5$ 且 $\left|F_e\right|\le n-3$ 时， $B_n-F_e$ 中每个点x的局部诊断度等于它的度。由引理6.7， $B_n-F_e$ 中的每个点都具有强局部诊断性。由引理6.8， $B_n-F_e$ 有强局部诊断性。

现在我们给出了一个例子来证明如果存在 $n-2$ 条遗失边F，n维泡型图 $B_n$ 可能不具有强局部可诊断性。对于 $B_n$ 中的任意顶点x，x被标记为 $\left[n\right]$ 上的一个置换。假设 $B_n$ 中有 $n-2$ 条遗失边的边F，它们与x相关联(如图6所示)，那么在 $B_n-F$ 中x的度就变成了1。假设y是x的唯一的邻点。设 $\left|F_1\right|=\left(\left\{y\right\}\cup N\left(y\right)\right)\backslash \left\{x\right\}$， $\left|F_2\right|=N\left(y\right)$。此时 $\left|F_1\right|=\left|F_2\right|=n-1$。显然， $V\left(B_n-F\right)\backslash \left(F_1\cup F_2\right)$ 和 $F_1\Delta F_2$ 之间没有边，那么顶点集对 $\left(F_1,F_2\right)$ 不满足引理6.9中的条件(1)~(3)，因此在MM*模型下， $B_n-F$ 在顶点y处不是 $\left(n-1\right)$ -局部可诊断的。由于在 $B_n-F$ 中，顶点y的局部可诊断度(小于 $n-1$ )与它的度(等于 $n-1$ )不相等，因此顶点y不再具有强局部可诊断性。因此，具有 $n-2$ 条遗失边的泡型图 $B_n$ 不能保证具有强局部可诊断性。

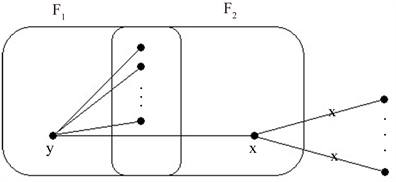
Figure 6. Illustration of the proof in Theorem 7.2 and Theorem 8.2

图6. 定理7.2和8.2中的证明说明

8. n维修正泡型图MB_n的诊断度

引理8.1 令x是n维修正泡型图 $M{B}_n\left(n\ge 7\right)$ 中的任意一个顶点，在 $M{B}_n$ 中存在一个以x为根的扩展星图 $ES\left(x;n\right)$。

证明 我们可以将 $M{B}_n$ 分解为n个不相交的子图 $M{B}_n^1$， $M{B}_n^2$， $\cdots$， $M{B}_n^n$，其中每个顶点 $u=u_1{u}_2\cdots u_n\in V\left(M{B}_n\right)$ 的最后一个位置 $u_n$ 为一个固定的整数i，其中 $i\in \left[n\right]$。显然， $M{B}_n^i$ 同构于 $B_{n-1}$，其中 $B_{n-1}$ 是一个 $\left(n-1\right)$ 维的泡型图。

我们需找到一个扩展星图 $ES\left(x;n\right)$ 作为n维修正泡型图 $M{B}_n$ 在给定顶点x处的子图。由命题5.1， $M{B}_n$ 是顶点传递的。不失一般性，令 $x=12\cdots n=\left(1\right)$ 作为扩展星图 $ES\left(\left(1\right);n\right)$ 的一个根。由引理7.1，对于 $n\ge 5$ 时的泡型图 $B_n$，在 $B_n$ 中存在一个以x为根的扩展星图 $ES\left(\left(1\right);n-1\right)$。因此在 $M{B}_n^n$ 中存在一个以x为根的扩展星图 $ES\left(x;n-1-1\right)$。注意 $\left(1\right)$ 有两个外部邻点 $\left(1n\right)$ 和 $\left(n-1,n\right)$，其中 $\left(1n\right)\in V\left(M{B}_n^1\right)$， $\left(n-1,n\right)\in V\left(M{B}_n^{n-1}\right)$。注意在 $M{B}_n^1$ 中存在一条三长路 $P_1=\langle \left(1n\right),\left(12n\right),\left(123n\right),\left(1234n\right)\rangle$，在 $M{B}_n^{n-1}$ 中存在一条三长路 $P_2=\langle \left(n-1,n\right),\left(12\right)\left(n-1,n\right),\left(123\right)\left(n-1,n\right),\left(123\right)\left(45\right)\left(n-1,n\right)\rangle$。连接 $P_1$ 和 $P_2$ 到x，并结合扩展星图 $ES\left(x;n-2\right)$。因此我们就在 $M{B}_n$ 中找到了一个以 $\left(1\right)$ 为根的扩展星图 $ES\left(\left(1\right);n\right)$，即在 $M{B}_n$ 中存在一个以x为根的扩展星图 $ES\left(x;n\right)$。

定理8.1 设 $M{B}_n\left(n\ge 7\right)$ 是一个n维修正泡型图，则 $M{B}_n$ 的诊断度为n，即 $t\left(M{B}_n\right)=n$ 并且 $M{B}_n$ 具有强局部可诊断性。

证明 由引理6.5和8.1， $M{B}_n$ 中每个顶点x的局部诊断度都是n。由引理6.3， $M{B}_n$ 的诊断度为n，即 $t\left(M{B}_n\right)=n$。由于 $M{B}_n$ 中每个顶点x的度是n，那么 $M{B}_n$ 中每个顶点的局部可诊断性等于其在 $M{B}_n$ 中的度。由引理6.7， $M{B}_n$ 中的每个顶点x都具有强局部可诊断性。由引理6.8， $M{B}_n$ 具有强局部可诊断性。

引理8.2设 $F_e$ 是 $M{B}_n\left(n\ge 7\right)$ 中任意的遗失边集且 $\left|F_e\right|\le n-2$。x是 $M{B}_n\left(n\ge 7\right)$ 中的任意一个顶点，在中存在一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$，其中 $x\in V\left(M{B}_n\right)$。

证明 根据命题5.1， $M{B}_n$ 是顶点传递的。不失一般性，令 $x=12\cdots n=\left(1\right)$ 作为扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$ 的一个根。我们可以将 $M{B}_n$ 分解为n个不相交的子图 $M{B}_n^1$， $M{B}_n^2$， $\cdots$， $M{B}_n^n$，其中每个顶点 $u=u_1{u}_2\cdots u_n\in V\left(M{B}_n\right)$ 的最后一个位置 $u_n$ 为一个固定的整数i，其中 $i\in \left[n\right]$。显然， $M{B}_n^i$ 同构于 $B_{n-1}$，其中 $B_{n-1}$ 是一个 $\left(n-1\right)$ 维的泡型图。

设 $F_e^i=F_e\cap E\left(M{B}_n^i\right)\left(1\le i\le n\right)$， $F^{*}=F_e\cap E\left(M{B}_n\right)\backslash {\displaystyle {\sum }_{i=1}^{n}E\left(M{B}_n^i\right)}$，那么 $F_e=F^{*}\cup F_e^1\cup \cdots \cup F_e^n$。为了方便，设 $\tilde{F}=F^{*}\cap \left\{xu,xv\right\}$， $\left(1\right)$ 有两个外部邻点 $\left(1n\right)$ 和 $\left(n-1,n\right)$。为了证明这个引理，我们需要讨论 $\tilde{F}$ 是否为空集。当 $\tilde{F}=\varnothing$ 时，第一步是在 $M{B}_n^n-F_e^n$ 中找到一个扩展星图 $ES\left(x;d_{M{B}_n^n-F_e^n}\left(x\right)\right)$ ；第二步是在 $M{B}_n^1$ 中找到一条三长路 $P_u$，在 $M{B}_n^{n-1}$ 中找到一条三长路 $P_v$ ；第三步是连接 $P_u$ 和 $P_v$ 到x。然后我们可以在 $M{B}_n-F_e$ 中找到一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$。当 $\tilde{F}\ne \varnothing$ 时，我们从 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$ 中删除以x为起点且包含任意边 $\tilde{F}$ 的四长路，从而得到一个满足引理的扩展星图。

需要注意的是，在本文中从图G中删除一条四长的路径P意味着从图G中删除除顶点y之外的所有四长的路径中的顶点和边，其中y是P和G的唯一公共顶点。

首先，我们给出如下两个断言。

断言1 如果 $\left|F_e^i\right|\le n-4$，那么对于 $z\in V\left(M{B}_n^i\right)$ 在 $M{B}_n^i-F_e^i$ 中存在一个以z为根的扩展星图 $ES\left(z;d_{M{B}_n^i-F_e^i}\left(z\right)\right)$。在只有公共顶点z的扩展星图 $ES\left(z;d_{M{B}_n^i-F_e^i}\left(z\right)\right)$ 中，存在至少 $\left(n-2-\left|F_e^i\right|\right)$ 条四长路(三长路)，最多 $\left(n-2\right)$ 条四长路(三长路)。

证明 注意 $M{B}_n^i$ 同构于 $B_{n-1}$ 且 $\left|F_e^i\right|\le n-4=n-3-1$，由引理7.2，当 $z\in V\left(M{B}_n^i\right)$ 且 $d_{M{B}_n^i}\left(z\right)=n-2$ 时，在 $M{B}_n^i-F_e^i$ 中存在一个以z为根的扩展星图 $ES\left(z;d_{M{B}_n^i-F_e^i}\left(z\right)\right)$。因此， $d_{M{B}_n^i}\left(z\right)\ge n-2-\left|F_e^i\right|$，结合扩展星图的定义，我们可以在只有公共顶点z的扩展星图 $ES\left(z;d_{M{B}_n^i-F_e^i}\left(z\right)\right)$ 中找到至少 $\left(n-2-\left|F_e^i\right|\right)$ 条，最多 $\left(n-2\right)$ 条四长路(三长路)。特别是当且仅当 $F_e^i$ 中的每条边都与z相关时，在扩展星图 $ES\left(z;d_{M{B}_n^i-F_e^i}\left(z\right)\right)$ 中仅存在 $\left(n-2-\left|F_e^i\right|\right)$ 条四长路(三长路)。

断言2 如果 $\left|F_e^i\right|<n-2$，那么对于 $z\in V\left(M{B}_n^i\right)$ 在 $M{B}_n^i-F_e^i$ 中点z处存在至少一条三长路。

证明 由命题4.4， $\kappa \left(M{B}_n^i\right)=n-1-1=n-2$。因为 $M{B}_n^i$ 同构于 $B_{n-1}$，我们有 $\kappa \left(M{B}_n^i\right)=n-2$。注意 $\kappa \left(M{B}_n^i\right)=n-2>\left|F_e^i\right|$，因此我们可以得到 $M{B}_n^i-F_e^i$ 是连通的。由命题5.2和 $\left|V\left(M{B}_n^i\right)\right|-\left|F_e^i\right|>\left(n-1\right)\text{!}-\left(n-2\right)\ge 715\left(n\ge 7\right)$，所以对于 $z\in V\left(M{B}_n^i\right)$ 在 $ES\left(z;d_{M{B}_n^i-F_e^i}\left(z\right)\right)$ 中可以找到一条以z为起点的三长路。

然后我们通过讨论 $\left|F_e\right|$ 和 $\left|F_e^i\right|$ 找到扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$。

情形1 $\left|F_e^n\right|\le n-4$。

由断言1，在 $M{B}_n^n-F_e^n$ 中存在一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n^n-F_e^n}\left(x\right)\right)=A$。

情形1.1 $\left|F_e\right|<n-2$。

在这种情形下， $\left|F_e^i\right|<n-2\left(i\in \left\{1,n-1\right\}\right)$。由断言2，在 $M{B}_n^1-F_e^1\left(M{B}_n^{n-1}-F_e^{n-1}\right)$ 中存在一条三长路 $P_u\left(P_v\right)$。我们连接 $P_u$ 和 $P_v$ 到x，然后把它们与A相结合，于是，在 $M{B}_n-F_e$ 中可以得到一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$。如果 $\tilde{F}=\varnothing$，那么 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$ 满足引理。如果 $\tilde{F}\ne \varnothing$，我们从 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$ 中删除以x为起点且包含任意边 $\tilde{F}$ 的四长路，从而得到一个满足引理的扩展星图。

情形 1.2 $\left|F_e\right|=n-2$。

如果 $\left|F_e^1\right|$ 和 $\left|F_e^{n-1}\right|$ 都小于 $n-2$，我们可以按照情形1.1完成证明。显然， $\left|F_e^1\right|$ 和 $\left|F_e^{n-1}\right|$ 中最多只有一个等于 $n-2$，不失一般性，我们假设 $\left|F_e^1\right|=n-2$。那么 $\left|F^{*}\right|+\left|F_e^2\right|+\left|F_e^3\right|+\cdots +\left|F_e^{n-1}\right|+\left|F_e^n\right|=0$。注意 $P_u=\langle \left(1n\right),\left(1n\right)\left(n-1,n\right),\left(1n\right)\left(n-1,n\right)\left(12\right),\left(1n\right)\left(n-1,n\right)\left(12\right)\left(34\right)\rangle$，显然， $P_u-u$ 在 $M{B}_n^{n-1}$ 中。由断言1和 $\left|F_e^{n-1}\right|=0$，在 $M{B}_n^{n-1}$ 中存在 $\left(n-2\right)$ 条不包含遗失边三长路。注意 $v\notin V\left(P_u\right)$， $\left|V\left(P_u\right)\cap V\left(M{B}_n^{n-1}\right)\right|=3$ 且 $n-2>3\left(n\ge 7\right)$，因此在 $M{B}_n^{n-1}$ 中存在一条以v为起点的三长路 $P_v$，使得 $P_u$ 和 $P_v$ 没有公共顶点，并且 $P_u$ 和 $P_v$ 都不包含遗失边。我们连接 $P_u$ 和 $P_v$ 到x，然后把它们与A相结合，于是，在 $M{B}_n-F_e$ 中可以得到一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$。

情形 2 $\left|F_e^n\right|=n-3$， $\left|F_e\right|=n-3$。

在这种情形下， $\left|F^{*}\right|+\left|F_e^1\right|+\left|F_e^2\right|+\cdots +\left|F_e^{n-1}\right|=0$。由断言1，我们可以从 $M{B}_n^1\left(M{B}_n^{n-1}\right)$ 中至少 $\left(n-2\right)$ 条不包含遗失边的三长路中选择一条三长路 $P_u\left(P_v\right)$。设 $f\in F_e^n$ 且 ${F^{\prime }}_e=F_e^n\backslash \left\{f\right\}$。此时 $\left|{F^{\prime }}_e\right|=n-4$。由断言1，在 $M{B}_n^n-{F^{\prime }}_e$ 中存在一个扩展星图 $ES\left(x;d_{M{B}_n^n-{F^{\prime }}_e}\left(x\right)\right)$。假设 $A^{\prime }=ES\left(x;d_{M{B}_n^n-{F^{\prime }}_e}\left(x\right)\right)$。

情形 2.1 $f\notin E\left(A^{\prime }\right)$。

在这种情形下， $A^{\prime }$ 是 $M{B}_n^n-F_e^n$ 中以x为根的扩展星图 $ES\left(x;d_{M{B}_n^n-F_e^n}\left(x\right)\right)$ 中的一个。注意 $\left|F^{*}\right|=0$，因此我们连接 $P_u$ 和 $P_v$ 到x，然后把它们与 $A^{\prime }$ 相结合，于是，在 $M{B}_n-F_e$ 中可以得到一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$。

情形 2.2 $f\in E\left(A^{\prime }\right)$。

设 $P_x$ 是 $A^{\prime }$ 中的一条以x为起点且包含f的四长路。我们可以从 $A^{\prime }$ 中删除 $P_x$ 来得到A。

情形 2.2.1 f与x相关联。

注意 $\left|F^{*}\right|=0$，因此我们连接 $P_u$ 和 $P_v$ 到x，然后把它们与 $A^{\prime }$ 相结合，于是，在 $M{B}_n-F_e$ 中可以得到一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$。

情形 2.2.2 f与x不相关联。

设 $P_a$ 是一条以a为起点且包含f的三长路，则a与x相关联。接下来，我们考虑 $a=\left(i,i+1\right)\left(1\le i\le n-2\right)$。不失一般性，假设 $a=\left(12\right)$。注意 $\left|F_e^{n-1}\right|=0$，我们可以在 $M{B}_n^{n-1}$ 中选择一条不包含遗失边的二长路 $P_{a^{\prime }}=\langle a^{\prime },a^{\prime }\left(34\right),a^{\prime }\left(34\right)\left(n-4,n-3\right)\rangle$，其中 $a^{\prime }=\left(12\right)\left(n-1,n\right)$。由断言1和 $\left|F_e^i\right|=0$，我们可以在 $M{B}_n^i$ 中找到 $\left(n-2\right)$ 条三长路，其中 $i\in \left(1,n-1\right)$。注意 $v\notin V\left(P_{a^{\prime }}\right)$， $\left|V\left(P_{a^{\prime }}\right)\cap V\left(M{B}_n^{n-1}\right)\right|=3$ 并且 $n-2>3\left(n\ge 7\right)$，因此我们可以 $M{B}_n^{n-1}$ 中找到一条不包含遗失边的三长路 $P_v$，使得 $P_v$ 和 $P_{a^{\prime }}$ 没有公共顶点。同样，我们可以在 $M{B}_n^1$ 中找到一条三长路 $P_u$。将 $P_{a^{\prime }}$ 连接到a，可以得到一条以a为起点的三长路 $P_a$。注意 $P_a$， $P_u$ 和 $P_v$ 都不包含遗失边，且它们中的任意两个都没有公共顶点。我们连接 $P_a$， $P_u$ 和 $P_v$ 到x，然后把它们与A相结合，于是，在 $M{B}_n-F_e$ 中可以得到一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$。

情形 3 $\left|F_e^n\right|=n-3$， $\left|F_e\right|=n-2$。

注意 $\left|F^{*}\right|+\left|F_e^1\right|+\left|F_e^2\right|+\cdots +\left|F_e^{n-1}\right|=1$。由断言1，我们可以从 $M{B}_n^1\left(M{B}_n^{n-1}\right)$ 中至少 $\left(n-2\right)$ 条不包含遗失边的三长路中选择一条三长路 $P_u\left(P_v\right)$。设 $f\in F_e^n$ 且 ${F^{\prime }}_e=F_e^n\backslash \left\{f\right\}$。此时 $\left|{F^{\prime }}_e\right|=n-4$。由断言1，在 $M{B}_n^n-{F^{\prime }}_e$

中存在一个扩展星图 $ES\left(x;d_{M{B}_n^n-{F^{\prime }}_e}\left(x\right)\right)$。假设 $A^{\prime }=ES\left(x;d_{M{B}_n^n-{F^{\prime }}_e}\left(x\right)\right)$。

情形 3.1 $f\notin E\left(A^{\prime }\right)$。

在这种情形下， $A^{\prime }$ 是 $M{B}_n^n-F_e^n$ 中以x为根的扩展星图 $ES\left(x;d_{M{B}_n^n-F_e^n}\left(x\right)\right)$ 中的一个。因此我们连接 $P_u$ 和 $P_v$ 到x，然后把它们与 $A^{\prime }$ 相结合，于是，在 $M{B}_n-F_e$ 中可以得到一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$。注意 $\left|F^{*}\right|\le 1$。如果 $\tilde{F}=\varnothing$，那么 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$ 满足引理。如果 $\tilde{F}\ne \varnothing$，我们从 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$ 中删除以x为起点且包含任意边 $\tilde{F}$ 的四长路，从而得到一个满足引理的扩展星图。

情形 3.2 $f\in E\left(A^{\prime }\right)$。

设 $P_x$ 是 $A^{\prime }$ 中的一条以x为起点且包含f的四长路。我们可以从 $A^{\prime }$ 中删除 $P_x$ 来得到A。

情形 3.2.1 f与x相关联。

我们连接 $P_u$ 和 $P_v$ 到x，然后把它们与A相结合，于是，在 $M{B}_n-F_e$ 中可以得到一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$。注意 $\left|F^{*}\right|\le 1$。如果 $\tilde{F}=\varnothing$，那么 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$ 满足引理。如果 $\tilde{F}\ne \varnothing$，我们从 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$ 中删除以x为起点且包含任意边 $\tilde{F}$ 的四长路，从而得到一个满足引理的扩展星图。

情形 3.2.2 f与x不相关联。

若a与x相邻， $P_a$ 是一条以a为起点且包含f的三长路。

情形 3.2.2.1 $\left|F^{*}\right|=0$。

在这种情形下， $\left|F_e^1\right|+\left|F_e^2\right|+\cdots +\left|F_e^{n-1}\right|=1$。不失一般性，假设 $\left|F_e^1\right|=1$。接下来，我们考虑 $a=\left(i,i+1\right)\left(1\le i\le n-2\right)$。不失一般性，假设 $a=\left(12\right)$。注意 $\left|F_e^{n-1}\right|=0$，我们可以在 $M{B}_n^{n-1}$ 中选择一条不包含遗失边的二长路 $P_{a\text{'}}=\langle a^{\prime },a^{\prime }\left(34\right),a^{\prime }\left(34\right)\left(n-4,n-3\right)\rangle$，其中 $a^{\prime }=\left(12\right)\left(n-1,n\right)$。由断言1和 $\left|F_e^i\right|\le 1\left(i\in \left\{1,n-1\right\}\right)$，我们可以在 $M{B}_n^i$ 中找到 $\left(n-3\right)$ 条不包含遗失边的三长路，并且这些三长路中除了顶点 $u\left(v\right)$ 之外，任意的两条路都没有公共顶点。注意 $v\notin V\left(P_{a^{\prime }}\right)$， $\left|V\left(P_{a^{\prime }}\right)\cap V\left(M{B}_n^{n-1}\right)\right|=3$ 且 $n-2>3\left(n\ge 7\right)$，因此我们可以在 $M{B}_n^{n-1}$ 中找到一条不包含遗失边的三长路 $P_v$，使得 $P_v$ 和 $P_{a^{\prime }}$ 没有公共顶点。同样，我们可以在 $M{B}_n^1$ 中找到一条三长路 $P_u$。将 $P_{a^{\prime }}$ 连接到a，可以得到一条以a为起点的三长路 $P_a$。注意 $P_a$， $P_u$ 和 $P_v$ 都不包含遗失边，且它们中的任意两个都没有公共顶点。我们连接 $P_a$， $P_u$ 和 $P_v$ 到x，然后把它们与A相结合，于是，在 $M{B}_n-F_e$ 中可以得到一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$。

情形 3.2.2.2 $\left|F^{*}\right|=1$。

在这种情形下， $\left|F_e^1\right|+\left|F_e^2\right|+\cdots +\left|F_e^{n-1}\right|=0$。现在我们考虑 $a=\left(i,i+1\right)\left(1\le i\le n-2\right)$。不失一般性，假设 $a=\left(12\right)$。我们可以在 $M{B}_n^{n-1}$ 中选择一条不包含遗失边的二长路 $P_{{a^{\prime }}_1}=\langle {a^{\prime }}_1,{a^{\prime }}_1\left(34\right),{a^{\prime }}_1\left(34\right)\left(n-4,n-3\right)\rangle$，在 $M{B}_n^1$ 中找到一条二长路 $P_{{a^{\prime }}_2}=\langle {a^{\prime }}_2,{a^{\prime }}_2\left(34\right),{a^{\prime }}_2\left(34\right)\left(n-4,n-3\right)\rangle$，其中 ${a^{\prime }}_1=\left(12\right)\left(1n\right)$， ${a^{\prime }}_2=\left(12\right)\left(n-1,n\right)$。因为 $\left|F_e^1\right|=\left|F_e^{n-1}\right|=0$，因此我们可以从 $P_{{a^{\prime }}_1}$ 和 $P_{{a^{\prime }}_2}$ 中选择一条不包含遗失边的二长路 $P_{a^{\prime }}$。注意 $P_{{a^{\prime }}_1}$， $P_{{a^{\prime }}_2}$ 在不同的 $M{B}_n^i$ 中，并且 $\left|F^{*}\right|=1$，将 $P_{a^{\prime }}$ 连接到a，可以得到一条不包含遗失边的三长路 $P_a$。由断言1和 $\left|F_e^i\right|=0\left(i\in \left\{1,n-1\right\}\right)$，我们可以在 $M{B}_n^i$ 中找到 $\left(n-2\right)$ 条不包含遗失边的三长路，并且这些三长路中除了顶点 $u\left(v\right)$ 之外，任意的两条路都没有公共顶点。注意 $v\notin V\left(P_{a^{\prime }}\right)$， $\left|V\left(P_{a^{\prime }}\right)\cap V\left(M{B}_n^{n-1}\right)\right|=3$ 且 $n-2>3\left(n\ge 7\right)$。如果 $P_{a^{\prime }}=P_{{a^{\prime }}_2}$，那么我们可以在 $M{B}_n^1$ 中找到一条不包含遗失边的三长路 $P_u$，使得 $P_u$ 和 $P_{a^{\prime }}$ 没有公共顶点。同样，我们可以在 $M{B}_n^{n-1}$ 中找到一条不包含遗失边的三长路 $P_v$。如果 $P_{a^{\prime }}=P_{{a^{\prime }}_1}$，那么我们可以在 $M{B}_n^{n-1}$ 中找到一条不包含遗失边的三长路 $P_v$，使得 $P_v$ 和 $P_{a^{\prime }}$ 没有公共顶点。同样，我们可以在 $M{B}_n^1$ 中找到一条三长路 $P_u$。将 $P_{a^{\prime }}$ 连接到a，可以得到一条以a为起点的三长路 $P_a$。注意 $P_a$， $P_u$ 和 $P_v$ 都不包含遗失边，且它们中的任意两个都没有公共顶点。我们连接 $P_a$， $P_u$ 和 $P_v$ 到x，然后把它们与A相结合，于是，在 $M{B}_n-F_e$ 中可以得到一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$。注意 $\left|F^{*}\right|=1$。如果 $\tilde{F}=\varnothing$，那么 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$ 满足引理。如果 $\tilde{F}\ne \varnothing$，我们从 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$ 中删除以x为起点且包含任意边 $\tilde{F}$ 的四长路，从而得到一个满足引理的扩展星图。

情形 4 $\left|F_e^n\right|=n-2$， $\left|F_e\right|=n-2$。

在这种情形下， $\left|F^{*}\right|+\left|F_e^1\right|+\left|F_e^2\right|+\cdots +\left|F_e^{n-1}\right|=0$。由断言1，我们可以从 $M{B}_n^1\left(M{B}_n^{n-1}\right)$ 中至少 $\left(n-2\right)$ 条不包含遗失边的三长路中选择一条三长路 $P_u\left(P_v\right)$。设 $f,f^{\prime }\in F_e^n$， ${F^{\prime }}_e=F_e^n\backslash \left\{f,f^{\prime }\right\}$。此时 $\left|{F^{\prime }}_e\right|=n-4$。由断言1，在 $M{B}_n^n-{F^{\prime }}_e$ 中存在一个扩展星图 $ES\left(x;d_{M{B}_n^n-{F^{\prime }}_e}\left(x\right)\right)$。假设 $A^{\prime }=ES\left(x;d_{M{B}_n^n-{F^{\prime }}_e}\left(x\right)\right)$。

情形 4.1 f， $f^{\prime }$ 都不属于 $A^{\prime }$。

在这种情形下， $A^{\prime }$ 是 $M{B}_n-F_e$ 中以x为根的扩展星图 $ES\left(x;d_{M{B}_n^n-{F^{\prime }}_e}\left(x\right)\right)$ 中的一个。注意 $\left|F^{*}\right|=0$，因

此我们连接 $P_u$ 和 $P_v$ 到x，然后把它们与 $A^{\prime }$ 相结合，于是，我们在 $M{B}_n-F_e$ 中可以得到一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}(\; x\; )\right)$

情形 4.2 $A^{\prime }$ 包含f或 $f^{\prime }$。

不失一般性，我们假设 $A^{\prime }$ 包含f。设 $P_x$ 是 $A^{\prime }$ 中一条以x为起点且包含f的四长路。我们可以从 $A^{\prime }$ 中删除 $P_x$ 来得到A。接下来我们讨论f是否与x相关联。如果f与x相关联，那么接下来的证明与情形2.2.1相似。如果f不与x相关联，那么接下来的证明与情形2.2.2相似。

情形 4.3 $A^{\prime }$ 包含f和 $f^{\prime }$。

情形 4.3.1 f和 $f^{\prime }$ 都与x相关联。

设 $P_x\left(P_{x^{\prime }}\right)$ 是 $A^{\prime }$ 中一条以x为起点且包含 $f\left(f^{\prime }\right)$ 的四长路。我们可以从 $A^{\prime }$ 中删除 $P_x$ 和 $P_{x^{\prime }}$ 来得到A。注意 $\left|F^{*}\right|=0$，我们连接 $P_u$ 和 $P_v$ 到x。然后把它们与A相结合，于是，在 $M{B}_n-F_e$ 中可以得到一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$。

情形 4.3.2 f或 $f^{\prime }$ 与x相关联。

不失一般性，我们假设 $f^{\prime }$ 与x相关联。设 $P_x\left(P_{x^{\prime }}\right)$ 是 $A^{\prime }$ 中一条以x为起点且包含 $f\left(f^{\prime }\right)$ 的四长路。我们可以从 $A^{\prime }$ 中删除 $P_x$ 和 $P_{x^{\prime }}$ 来得到A。设 $P_a$ 是一条以a为起点且包含f的三长路，则a与x相关联，接下来的证明与情形2.2.2相似。

情形 4.3.3 f和 $f^{\prime }$ 都不与x相关联。

接下来我们考虑f和 $f^{\prime }$ 是否属于同一条路。

情形 4.3.3.1 f和 $f^{\prime }$ 属于 $A^{\prime }$ 中的同一条路。

接下来的证明与情形2.2.2相似。

情形 4.3.3.2 f和 $f^{\prime }$ 属于 $A^{\prime }$ 中的不同的路。

设 $P_a\left(P_b\right)$ 是一条从 $a\left(b\right)$ 开始且包含 $f\left(f^{\prime }\right)$ 的三长路，则a和b都与x相关联。注意 $\left|F_e^n\right|=n-2$ 且 $\left|F_e\right|=n-2$。我们很容易在 $M{B}_n^1\left(M{B}_n^{n-1}\right)$ 中找到一条不包含遗失边的二长路 $P_{a^{\prime }}\left(P_{b^{\prime }}\right)$，并且 $P_{a^{\prime }}\left(P_{b^{\prime }}\right)$ 和 $P_u\left(P_v\right)$ 没有公共点。将 $P_{a^{\prime }}\left(P_{b^{\prime }}\right)$ 连接到 $a\left(b\right)$，可以得到一条以 $a\left(b\right)$ 为起点的三长路 $P_a\left(P_b\right)$。注意 $\left|F^{*}\right|=0$，我们连接 $P_a$， $P_b$， $P_u$ 和 $P_v$ 到x，然后把它们与A相结合，于是，然后把它们与A相结合，于是，在 $M{B}_n-F_e$ 中可以得到一个以x为根的扩展星图 $ES\left(x;d_{M{B}_n-F_e}\left(x\right)\right)$。

定理 8.2 设 $F_e$ 是n维修正泡型图 $M{B}_n\left(n\ge 7\right)$ 中的任意边子集且 $\left|F_e\right|\le n-2$。对 $M{B}_n$ 中的每个点x， $M{B}_n-F_e$ 具有强局部诊断性，其中 $F_e$ 的个数是最优的。

证明 由引理6.5和8.2，当 $n\ge 7$ 且 $\left|F_e\right|\le n-2$ 时， $M{B}_n-F_e$ 中每个点x的局部诊断度等于它的度。由引理6.7， $M{B}_n-F_e$ 中的每个点都具有强局部诊断性。由引理6.8， $M{B}_n-F_e$ 具有强局部诊断性。

现在我们给出一个例子来证明如果存在 $n-1$ 条遗失边F，n维修正泡型图 $M{B}_n$ 可能不具有强局部可诊断性。对于 $M{B}_n$ 中的任意顶点x，x标记为 $\left[n\right]$ 上的一个置换。假设 $M{B}_n$ 中有 $n-1$ 条遗失边F，它们与x相关联(如图6所示)，那么在 $M{B}_n-F$ 中x的度就变成了1。假设y是x的唯一的邻点。设 $\left|F_1\right|=\left(\left\{y\right\}\cup N\left(y\right)\right)\backslash \left\{x\right\}$， $\left|F_2\right|=N\left(y\right)$。此时 $\left|F_1\right|=\left|F_2\right|=n$。显然， $V\left(M{B}_n-F\right)\backslash \left(F_1\cup F_2\right)$ 和 $F_1\Delta F_2$ 之间没有边，那么顶点集对 $\left(F_1,F_2\right)$ 不满足引理6.9中的条件(1)~(3)，因此在MM*模型下， $M{B}_n-F$ 在顶点y处不是n-局部可诊断的。由于在 $M{B}_n-F$ 中，y的局部可诊断度(小于n)与它的度(等于n)不相等，因此顶点y不再具有强局部可诊断性。因此，具有 $n-1$ 条遗失边的修正泡型图 $M{B}_n$ 不能保证具有强局部可诊断性。

9. 结论

系统的诊断度是衡量系统容错性的重要参数。在这篇文章中，我们研究了n维泡型图 $B_n$ 和n维修正泡型图 $M{B}_n$ 在MM*模型下的局部诊断度。我们证明了n维泡型图 $B_n$ 的诊断度是 $n-1$，n维修正泡型图 $M{B}_n$ 的诊断度是n，以及即使 $B_n$ 和 $M{B}_n$ 中分别存在高达 $n-3$ 和 $n-2$ 条遗失边，它们仍保持这种强的性质。因此，在n维泡型图 $B_n$ 和n维修正泡型图 $M{B}_n$ 的遗失边数分别不超过 $n-3$ 和 $n-2$ 的条件下，它们的诊断度等于每个处理器剩余度的最小值。

致谢

本论文是在我的导师王世英教授的悉心指导下完成的。他渊博的专业知识，严谨的治学态度，精益求精的工作作风，诲人不倦的高尚师德，严于律己、严以律己、宽以待人的崇高风范，朴实无华、平易近人的人格魅力对本人影响深远。不仅使本人树立了远大的学习目标，掌握了基本的研究方法，还使本人明白了许多为人处事的道理。本次论文从选题到完成，每一步都倾注了导师大量的心血。在写论文的过程中，遇到了很多的问题，在王老师的耐心指导下，问题都得以解决。在此，谨向王老师表示崇高的敬意和衷心的感谢！同时，感谢同门和舍友在我学习和生活上给予的帮助和关心，谢谢！。

基金项目

国家自然科学基金资助项目(61772010)。

NOTES

^*通讯作者。