1. 引言
近些年随着科技的发展,图像视觉伺服(Image-Based Visual Servoing)的移动机器人(Wheeled Mobile Robot)备受关注。传统的IBVS中存在图像雅可比矩阵奇异性与局部发散的问题 [1];Cheah [2] 提出了深度信息的在线估计方法,在此基础上Liu [3] 提出了深度无关雅可比矩阵,使得未知参数可以被线性化。当系统存在未知扰动时,不再满足参数线性化的条件,滑模控制(Sliding Mode Control)成为了更好的选择 [4],SMC具有对参数摄动和外界扰动不灵敏等特点,张 [5] 使用SMC设计了足式移动机器人的控制方案;陈 [6] 提出了一种全局稳定定理与指数趋近律相结合的滑模控制方法;方 [7] 采用支持向量机耦合改进粒子群算法优化滑模控制器,减小了轨迹跟踪误差提高了鲁棒性。传统SMC中会出现抖振的现象,超螺旋滑模控制(Super Twisting Sliding Mode Control)是高阶滑模的一种,这种方式使产生不连续控制量作用于滑模量的高阶导数上,这样得到的控制率会包含积分项,通过积分的率波功能对抖振起到抑制;STSMC已被应用在无人机 [8]、导弹制导 [9] 等领域。
在IBVS的实际应用中,控制模块、固定摄像机和WMR往往通过一个带宽有限的无线网络连接,量化分辨率很粗糙,应考虑量化对系统稳定性的影响。薛 [10] 针对量化器灵敏度参数不匹配的系统研究了监督策略下的量化反馈滑模镇定控制问题;薛等人 [11] 通过建立量化参数的时变比例模型,设计自适应滑模控制方案;Sun [12] 使用扰动观测器,提出一种量化反馈系统的固定时间收敛控制方案。
针对具有量化和未知扰动的IBVS移动机器人轨迹跟踪问题,提出一种基于超螺旋算法的量化反馈控制方案,将未知扰动放入滑模切换函数的二阶导数中,对扰动连续补偿,接着将量化误差的界限放入滑模切换函数中,采用动态量化方案来使系统稳定,最终通过李雅普诺夫函数证明了系统的稳定性,仿真结果验证了控制方案的有效性。
2. 视觉伺服WMR系统
IBVS系统如图1所示,WMR在天花板具有固定摄像机的全局坐标系下,p为相机捕捉的特征点,将WMR前进速度v与转向角速度w看作控制输入,
为特征点p全局坐标。
基于非完整约束运动学模型可表示为
(1)
IBVS系统为:
(2)
(3)
为深度,
是可逆的 [3]
为图像系坐标,
为模型不确定、参数不确定和外界扰动的总和,WMR在图像系下的期望轨迹为
图像系下的误差定义为
(4)
设计如下PI型滑模函数
(5)
为待设定参数,对(5)求导可得
(6)
结合超螺旋算法设计如下控制器
(7)
(6)改写为
(8)
假设1:
连续可导且
,其中
是与时间相关的有界函数,满足
。
3. 量化反馈STSMC
考虑闭环系统通过网络传输信号如图2所示,控制器两端的信号会受到量化的影响,使用均匀量化方案 [13] 对系统状态量化
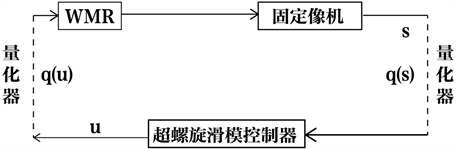
Figure 2. Quantitative feedback visual servo closed-loop system
图2. 量化反馈的视觉伺服闭环系统
(9)
为量化参数,
表示就近取整运算,量化误差为
(10)
由(10)可知
(11)
由图2可知信号传输将受到量化,(8)改写为
(12)
根据柯西不等式有如下关系
(13)
当
时
,当
时
,将(12)改写为
(14)
通过计算可得
。
定理1:对于系统(14),如果选择控制增益满足如下形式
(15)
系统状态将在有限时间
内收敛到区域
(16)
(17)
其中
为最小、最大特征根,
,矩阵
的形式将在证明中给出,
为P中的元素。
证明:对(16)求导可得
(18)
定义李雅普诺夫函数
(19)
其中
(20)
对(19)求导
(21)
由假设1可知
,且
,可得
(22)
其中
(23)
由Shur补的性质可知当参数选取满足(16)时
为正定矩阵,
满足不等式
(24)
且
,
由此可得
(25)
当
时有
(26)
由有限时间收敛理论 [14] 可得,存在时间
使
时有
,即系统将在有限时间
内,从任意初始位置收敛至
内
(27)
定理2:当满足条件(15)时,使用动态均匀量化方案
调节量化参数,系统状态(14)将会收敛至零,其中为
已知参数,
。
证明:由(17)可知
单调递增且
,即
时
,动态调节
,
时有
,
,
。由定理1可知,系统状态的收敛区域为
,在量化参数的动态调节的过程中,系统状态的收敛域将会不停更新,当
,
,
,
,可得系统状态
。
综上所述,在系统状态将收敛至
,通过动态量化方案使收敛区域
,最终系统会收敛至零,有
时
,由(5)可知
,当
时有
,扰动
可以在(15)的条件下受到连续的补偿,完成轨迹跟踪的任务。
针对系统控制输入,考虑与系统状态通过同一网络在闭环反馈系统中传输,使用(9)中量化方案对u进行量化,
,(14)改写为
(28)
其中
,
,
为量化参数,(28)被改写
(29)
定理2:系统(29)将会在有限时间内收敛至
(30)
证明过程同定理1,使用定理2可使
时有
,即系统(29)可渐进收敛至零。
4. 数值与仿真
期望轨迹
,初始坐标
,量化参数
,
,控制增益
,
,
,单应矩阵
,
。仿真时间为3 s,由图3可看出,使用动态量化方案的系统状态可在0.035 s收敛至定理1中的理论边界内做滑模运动,在动态量化参数调节的作用下快速收敛至0,抖振也明显减少;图4为动态调节下的量化输入;图5展示了具有动态量化状态和输入的IBVS移动机器人的轨迹跟踪误差,误差在0.028内;图6展示了在图像系中特征点运动轨迹与期望轨迹,可看出该控制方案拥有良好的轨迹跟踪性能。
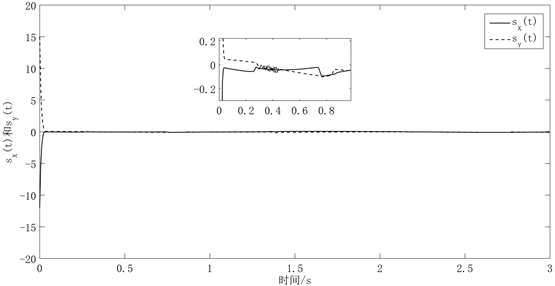
Figure 3. Dynamic uniform quantization of the system state
图3. 动态均匀量化的系统状态
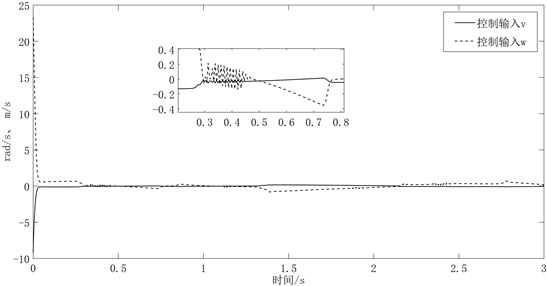
Figure 4. Dynamic uniform quantization of control inputs
图4. 动态均匀量化的控制输入
图7为静态量化下的系统状态,与图3对比可看出,系统状态在超螺旋算法的作用下仍会收敛于定
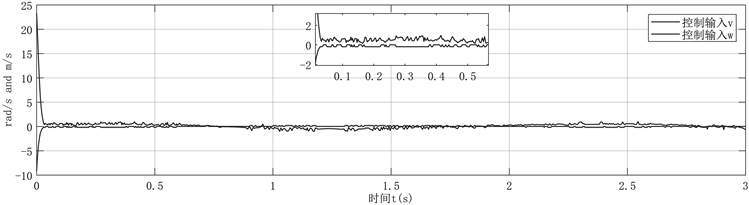
Figure 7. The state of the system under static quantization
图7. 静态量化下的系统状态
理一中与量化参数相关的较小区域,但存在明显地稳态误差;图8为静态量化的系统输入,在静态调节下控制输入存在明显抖振,图9为静态量化的轨迹跟踪误差,在未经动态调节的控制方案下,量化导致误差无法像图5中良好的收敛于领域。

Figure 8. Control input under static quantization
图8. 静态量化下的控制输入

Figure 9. Systematic error under static quantization
图9. 静态量化下的系统误差
5. 总结
提出一种基于超螺旋算法的量化反馈控制方案;给出存在未知扰动的IBVS系统收敛于与量化参数相关区域的参数条件,通过动态调节量化参数的方法,使系统状态可以收敛于零;通过李雅普诺夫函数证明了系统的稳定性,通过与静态量化控制方案对比的仿真可以看出该控制方案拥有良好的轨迹跟踪性能,具备良好的鲁棒性,收敛速度快且抖振得到有效地抑制。