基于随机森林的用户网购行为数据填充方法研究

Research on Data Filling Method of User Online Shopping Behavior Based on Random Forest

摘要: 本文针对用户网络购物行为预测问题，研究使用随机森林方法对用户网购行为数据进行填充。首先通过数据分析对数据集中缺失数据的缺失分布、缺失数量以及缺失数据存在依赖性进行分析，结合成对删除、对象删除的方法处理简单缺失数据，再重构数据集，基于随机森林方法对缺失数据进行填补。最后使用不同算法搭建用户网购行为预测模型，对比填补前后的数据集在这些模型下的预测效果，证明了随机森林方法在填补用户网购行为缺失数据中的有效性与通用性。

Abstract: Aiming at the prediction of user online shopping behavior, this paper studies the filling of user online shopping behavior data by using random forest method. Firstly, through data analysis, the missing distribution, missing quantity and the dependence of missing data in the data set are analyzed. Combined with the methods of paired deletion and object deletion, the simple missing data are processed, and then the data set is reconstructed to fill the missing data based on the random forest method. Finally, different algorithms are used to build user online shopping behavior prediction models, and the prediction effects of the data sets before and after filling are compared under these models, which proves the effectiveness and universality of the random forest method in filling the missing data of user online shopping behavior.

1. 引言

随着经济的发展，网络购物已经成为一种流行的购物方式。通过网络购物的形式，商家能够克服传统销售模式中与消费者的信息差，跨越空间售卖商品。为了更好地帮助商家进行营销，减小决策风险与运营成本，预测消费者的网络购买行为获得了越来越多学者的关注。通过分析网络购物中海量的商品信息与用户行为信息，对这些数据进行过滤与整理，选择合适的算法构建模型，从而能够预测用户接下来的消费行为 [1] [2] [3]。然而这些数据因为用户行为的复杂性，往往会有大量的缺失。若一味地强行删除，有可能会破坏原始数据结构，造成大量有效信息地丧失。因此，正确有效地处理缺失数据成为了问题的关键。

当前缺失数据的处理方法可以分为三种：忽略缺失、删除缺失值、填补缺失值 [4]。其中，删除缺失值包括对象删除、属性删除、成对删除这三种方法。在缺失值的处理中，填补缺失值受到了大量国内外学者的关注，主要可以分为统计学方法和机器学习方法 [5]。统计学方法基本上是基于原始数据集作出假设，然后利用统计学知识对缺失数据进行填补。这种方法由于没有考虑到数据本身的类别，计算出的填充值通常会受到其他数据的干扰，预测准确性较差。常见的方法有均值填充 [6] [7]、EM填充算法 [8] 以及多重插补法 [9] 等。机器学习方法则一般需要对原始数据进行重构，然后基于原始数据集通过各种机器学习方法训练模型预测缺失值 [10] [11]。常用于填补缺失值的机器学习方法有KNN算法 [12]、K-means算法、贝叶斯网络算法、随机森林算法 [13] [14] 等等。

基于此，本文针对用户网络购买行为数据的缺失填补问题展开研究。首先通过数据分析方法对数据集中缺失数据进行分析，结合分析结果重构数据集，然后基于随机森林方法对缺失数据进行填补。最后比较数据集填补前后在不同算法下的预测效果，验证填补方法的有效性。

2. 用户网购行为数据分析

本文所使用的数据集来自天池大数据众智平台，该数据集包含用户基本信息、用户-商品互动信息、商品基本信息等。接下来根据本文所研究的问题对数据集进行分析。

由于原始数据集是从淘宝网站中随机抽样的114万用户22天内的购物行为，仅行为数据就有7亿条数据，共23 G。因此为了实现大数据文件的读取，需要通过限制读取数量，分割数据块来完成数据读取。再从各个子数据块中根据用户出现次数按比例抽取用户行为数据，并将数据合并，最后得到一个包含近30万条数据的用户行为数据集来进行数据分析，用户出现次数基本符合正态分布。

首先为了了解数据集中各特征的缺失情况，对数据集中无效矩阵的数据密集程度进行了分析，随机抽取其中1万条数据进行展示，结果如图1所示。

Figure 1. Diagram of missing distribution about data set

图1. 数据集缺失分布图

如图所示，可以发现缺失数据主要分布在“price”、“final_gender-code”、“age_level”、“pvalue_level”、“shopping_level”、“occupation”、“new_user_class_level”这几个特征中。尤其是“price”、“pvalue_level”、“new_user_class_level”这三个特征数据缺失比较严重。这三个特征分别代表商品价格、用户消费档次、用户居住城市等级，与本课题将要预测的用户网购行为息息相关，因此具有填充研究价值。

为了获取缺失特征的缺失数字指标，根据数据集缺失分布情况，统计数据集中缺失特征的缺失数量，结果如图2所示。

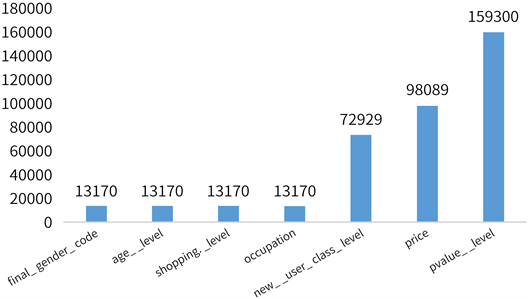
Figure 2. Diagram of missing feature quantity statistics

图2. 缺失特征数量统计图

如图所示可以发现，“price”、“pvalue_level”、“new_user_class_level”这三个特征缺失数据占比均超过25%，尤其是“pvalue_level”特征缺失数据占比超过50%。若一味删除，势必会造成大量有效数据的流失，因此必须要选择合适的方法来进行数据填充。此外，观察图2可以发现“final_gender-code”、“age_level”、“shopping_level”、“occupation”这四个特征的缺失占比虽然不大，但缺失数量相同。

为了更深层地探究各缺失特征之间的关系，分析出哪些特征需要进行填充，通过绘制热力图测量各缺失特征的空值相关性，探究变量的存在或不存在对另一个变量存在的影响程度。结果如图3所示。

Figure 3. Existence correlation of missing features

图3. 缺失特征存在相关性

首先可以发现特征“price”与其他特征并无存在相关性，因此对该特征直接进行对象删除操作。此外，“final_gender-code”、“age_level”、“shopping_level”、“occupation”这四个特征的存在相关性系数为1，这意味着这四个特征同时存在或者同时缺失，对于这样的数据，也无需填充，可以直接成对删除。因此，通过分析可知最终需要填充的特征为“pvalue_level”、“new_user_class_level”这两个特征。由上表可知这两个特征的存在相关性并不高，因此选择采用逐个填充的方法来进行填充。

3. 基于随机森林算法的用户网购行为数据填补

3.1. 随机森林算法

集成学习通过构建多个弱学习器，然后再采用某种结合策略，将所有弱学习器结合为一个强学习器来完成分类任务 [15] [16]。随机森林方法是集成学习中的一个子类，它的工作原理是训练多棵决策树进行预测，然后通过投票选择出现次数最多的类别即可完成分类。

随机森林的构造可以拆分为以下三个步骤，首先基于bootstrap sample采样方法构建决策树的训练样本集，每一次抽样都基于完整数据集进行，多次抽样后生成一系列bootstrap伪样本，从而能无偏地接近总体的分布。令D为 $X\times y$ 上的一个分布，训练集 $V={\left\{\left(X_i,y_i\right)\right\}}_{i=1}^N$ 是分布D上的一个子集。对训练集V有放回地抽取N次，每次抽取一条数据，即可得到一个包含 条数据的集合 $h={\left\{\left(X_i,y_i\right)\right\}}_{i=1}^N$， $h\in V$。重复以上步骤p次，即可获得一个包含p个训练集的集合 $H={\left\{h_i\right\}}_{i=1}^p$，其中，每个训练集 $h_i$ 都对应作为一棵决策树的训练样本集。

接着进行决策树构建，基于特征把数据划分到若干个子区域，再对子区域递归划分，直到节点的数据都是同一类的时候则停止划分并作为叶子节点。假设样本集中的样本包含M个特征，随机从M个特征中选择m个特征，其中 $m\ll M$。然后从这m个特征中选择信息增益最大的特征作为节点不断进行分裂。其中，信息增益代表熵的变化程度。信息增益越大，熵越大，分类效率越高 [17] [18]。

重复以上步骤建立大量决策树构成随机森林，最后通过投票即可完成分类。

3.2. 基于随机森林方法填补缺失值

由于本文所研究的用户网购行为问题场景复杂数据量大，用户购买浏览等操作分布不平衡，且因数据埋点失效造成一定程度上的数据缺失，而随机森林方法训练速度快，能有效地在大数据集上运行，对于不平衡的数据集，可以平衡误差维持精度。同时，利用随机森林构造多棵决策树完成填补，使得预测结果具有随机性与不确定性 [19]，更能反映出数据的真实分布，因此本文采用随机森林方法填补数据。

通过转换特征与标签的关系，将缺失特征重定为新的标签作为输出，将原标签与剩余特征重构为新的特征空间，构建出新的训练数据集作为输入，然后通过随机森林方法完成预测，即可实现数据的填补，得到一个完整的数据集。

由于用户网购行为数据集中缺失特征的存在相关性并不高，因此选择采用逐个填充的方法来进行填充。以下以用户消费等级特征“pvalue”的填充为例说明特征填充的操作步骤：

步骤1 处理非填补缺失值由于特征“price”与特征“pvalue”并无存在相关性，因此将特征“price”中存在缺失的数据进行对象删除操作。由于其他缺失特征均为类别型变量，因此采用众数填补法完成填充，得到一个除了特征“pvalue”以外没有缺失的数据集。

步骤2 重构数据集将特征“pvalue”定义为标签，将原标签与剩余特征定义为特征集，重新划分数据集，获得新的特征集 $X={\left\{\left(x_{i_1},\cdots ,x_{i_m}\right)\right\}}_{i=1}^N$，新的标签 $y=\left\{y_1,\cdots ,y_N\right\}$。然后根据标签y的缺失情况将数据集分为预测训练集 $T={\left\{\left(X_i,y_i\right)\right\}}_{i=1}^l$ 与待预测集 $W={\left\{\left(X_i,y_i\right)\right\}}_{i=1}^k$，其中 $l+m=N$。最后按照7:3的比例将预测训练集 $T={\left\{\left(X_i,y_i\right)\right\}}_{i=1}^l$ 划分为训练集与验证集。

步骤3 训练模型并预测缺失值基于训练集使用随机森林方法训练模型，并基于模型在验证集上的表现不断调参，获得一个较为理想的随机森林模型。然后将该模型应用到待预测集 $W={\left\{\left(X_i,y_i\right)\right\}}_{i=1}^k$ 中，获得特征“pvalue”的填补结果。

步骤4 填补原始数据集将填补完毕的待预测集 $W={\left\{\left(X_i,y_i\right)\right\}}_{i=1}^k$ 与预测训练集 $T={\left\{\left(X_i,y_i\right)\right\}}_{i=1}^l$ 合并得到无缺失的数据集 $S={\left\{\left(X_i,y_i\right)\right\}}_{i=1}^N$，然后根据其他特征的值将数据集 $S={\left\{\left(X_i,y_i\right)\right\}}_{i=1}^N$ 与原始数据集 $V={\left\{\left(X_i,y_i\right)\right\}}_{i=1}^N$ 建立对应关系，将数据集S的特征“pvalue”替换原始数据集 中的特征“pvalue”，完成原始数据集 $V={\left\{\left(X_i,y_i\right)\right\}}_{i=1}^N$ 基于随机森林方法对特征“pvalue”的填补。

4. 基于机器学习的用户网购行为预测模型

通过上述随机森林方法进行填补，获得了一个没有缺失值的用户网购行为数据集。通过该操作，保证了数据集的完整性，避免了有效信息的遗失。同时基于填补后的数据集，将用户未来是否会购买此商品定义为输出标签，以用户信息、商品信息及用户行为信息作为输入训练数据集，选择不同的算法即可搭建模型构造用户网购行为预测模型。

由于用户网购行为数据集样本容量大，各特征间多重共线性并不高，为了保证时间与内存的高效性，同时增加模型的通用性与多样性，选择使用最近邻(k-Nearest Neighbors, KNN)、逻辑回归(Logistic Regression, LR)、高斯朴素贝叶斯(GassianNB)和极端随机树(Extra-Trees, exTree)四种不同的机器学习算法构建用户网购行为预测模型。

其中，最近邻算法(k-Nearest Neighbors, KNN)主要靠周围有限的邻近的样本判别类别，而不是靠判别类域的方法来确定所属的类别，因此对于用户网购行为数据这类类域重叠较多的待分类样本集来说，KNN方法较其他方法更为适合；逻辑回归算法(Logistic Regression, LR)是一种对数线性模型，在时间和内存需求上相当高效，适用于处理本课题中的大型数据；高斯朴素贝叶斯算法(GassianNB)通过使用正态分布的概率密度函数来进行预测，对缺失数据不太敏感，算法也比较简单；而极端随机树算法(Extra-Trees, exTree)是RF的一个变种，也是由许多决策树构成，但exTree会随机地选择一个特征值来划分决策树，因为分裂是随机的，所以在某种程度上比随机森林得到的结果更加好。

通过以上四种不同的机器学习算法，建立用户网购行为信息与用户购买行为的映射关系，预测用户未来是否会购买此商品，从而帮助平台实现精准化营销。

5. 实验结果及分析

为了验证随机森林方法填补缺失值的有效性，针对使用随机森林方法填充缺失值的数据集以及不进行任何填补操作直接删除所有缺失值的数据集，分别使用KNN、LR、GassianNB、exTree四种不同的算法构建的用户网购行为预测模型进行用户购买行为预测。对比两个数据集基于不同算法模型在各评价指标下的表现如图4所示。

其中，准确率(accuracy)指标是最直观的衡量模型好坏的指标，它实际上是被正确预测的数据量比上所有参与预测的数据量的值；精确率和召回率(precision、recall)指标则分别反映了正确预测正例占真实正例和预测正例的比重，反映了模型查准与查全的能力；f1_score、roc_auc则结合了Precision与Recall两个指标综合考量模型预测性能。

Figure 4. Comparison of prediction effects of various algorithms before and after filling

图4. 填充前后各算法预测效果对比图

上图对比了KNN、LR、GassianNB、exTree四种算法作用在两种数据集下关于precision、recall、f1_score、roc_auc、accuracy这五个指标的表现。其中蓝色表示作用在基于随机森林方法填充缺失值的数据集上，橙色表示作用在不进行任何填补操作直接删除所有缺失值的数据集上。

可以发现，各算法基于填充缺失值的数据集的表现基本都优于直接删除缺失值的数据集。这其中预测效果表现最好的是exTree算法，两个数据集中各指标评分都高于0.95。两数据集的预测效果相差最小的是KNN算法，相差最大的是LR算法。是否填充对LR算法预测效果影响显著，填充后的数据集预测评分基本可以达到0.99以上，但未进行填充直接删除缺失值的数据集预测评分都低于0.8。唯一不填充效果好于填充效果的是GassianNB算法的precision指标评分，但两者相差并不显著，仅有0.005的差距，同时填充数据集在其他指标的表现都优于不填充数据集。

综上可以发现，各算法模型基于缺失值已填补的数据集的预测效果会更加好，证明了使用随机森林方法填补缺失值的必要性及有效性。

6. 结论

预测消费者的网络购买行为对电子商务平台来说具有重大现实意义，本文针对用户网络购买行为数据集常见的缺失问题展开研究。通过对缺失数据进行数据分析，制定填补策略。对于存在相关性极低或极高的特征分别进行对象删除与成对删除操作，针对相关性并不高的特征逐个采用随机森林方法进行填补操作。同时基于不同算法构建算法模型，通过分析各算法在填补前后的数据集上的表现，验证了随机森林方法填补缺失值的有效性及通用性。

该方法能有效填补缺失特征关联较小的数据集，但不适用于缺失特征相关性高的数据集。因此，将在未来研究中进一步基于缺失关联程度高的缺失数据填补展开研究。