基于剪切波变换的下卷积正则化SPECT图像重建

Infimal Convolution Regularized SPECT Image Reconstruction Based on Shearlet Transform

摘要: 单光子放射断层成像(SPECT)在疾病的影像诊断中起重要作用。全变差正则项在抑制噪声方面非常有效，但会产生阶梯状伪影。剪切波变换是一种多尺度几何分析方法，它比传统的小波变换更符合人类视觉系统的感知特性，能更有效地刻画和捕获图像中的边缘、纹理等几何特征，并能充分利用图像自身的几何特性实现对其更为“稀疏”的表示。本文提出一种基于下卷积剪切波变换惩罚项的SPECT重建方法，在抑制噪声的同时，进一步消除阶梯状伪影。实验结果表明，本文方法优于下卷积全变差惩罚项，图像边缘清晰、细节丰富，符合人眼视觉效果。

Abstract: Single-photon emission tomography (SPECT) plays an important role in the imaging diagnosis of the disease. Total variation regularization is more effective in suppressing noise but produces stair-step artifacts. Shearlet transformation is a multi-scale geometric analysis method. It is more in line with the traditional wavelet transform perception characteristics of the human visual system, and can more effectively depict and capture geometric feature texture in the image edge. It can make full use of the geometric characteristics of the image itself to its more sparse representation. In this paper, Infimal Convolution regularized SPECT image reconstruction based on shearlet transform is proposed, suppressing the noise and further eliminating stair-step artifact. Results show that the method is better than the infimal convolution total variation punishment. The reconstructed image has a clear edge and rich detail, which conforms to the human visual effect.

1. 引言

单光子放射断层摄影(SPECT)借助于单光子核素标记药物实现人体体内功能和代谢显像，在疾病的影像诊断中起重要作用。但高剂量的药剂会对患者的健康造成损害，增加致癌风险。因此需要减少医学成像包括SPECT中的放射性药剂。假设成像时间和伽玛相机保持不变，只有通过降低所给示踪剂的活性才能达到较低的辐射剂量。它会导致原始数据中的伽马光子较少，从而增加了重建图像中的图像噪声。因此，挑战是如何减少SPECT检查中的辐射剂量，而不会影响图像质量。这可以通过应用更好的放射性机构，改进的成像硬件或优越的重建方法来实现。最常用的描述SPECT投影数据的概率分布是泊松模型 [1]。在此模型的基础上，如何正确估计放射性分布是一个长期存在的研究问题。

本文提出下一种卷积剪切波变换惩罚项，与应用一阶二阶全变差正则项(ICTV)下卷积惩罚项 [2] 进行比较。我们进行仿真实验，使用小球模态和脑体模进行实验，以比较两种方法的重建图像的质量，并研究使用剪切波下卷积惩罚项方法降低患者辐射剂量的可行性。结果表明，本文方法优于下卷积全变差惩罚项，图像边缘清晰、细节丰富，符合人眼视觉效果。

2. 相关工作

2.1. 全变差正则项

SPECT图像重建是一个反问题，可以通过建立一个ECT成像系统(系统矩阵)，并通过应用变分方法与有效的最小化算法相结合。基于统计考虑的贝叶斯方法，依赖于后验概率(MAP)的最大化一个利用目标函数的负对数似然和关于解的先验知识的解。利用吉布斯先验分布的概念 [3]，重构问题可以被视为一个包含三项的凸优化问题前两项，统称为保真项，用于评估和惩罚预期数据和观测数据之间的匹配度(即评估拟合优度)，而最后一项，称为正则化项，惩罚低先验概率解。这两个项之间的平衡由一个正则化参数决定。正则化项需要反映未观察到的放射性示踪剂活性f的先验分布的统计特性关系，并应允许在抑制图像噪声的同时保留图像细节，包括尖锐的边缘。

其中一个常用的正则项是全变差正则项total variation (TV) [4]，全变差正规项是Panin等人 [5] 将其引入到SPECT重构中。然而，由于它只考虑一阶导数，即使原始图像只包含代表ECT活动分布的灰度值的平滑梯度，它也倾向于创建具有虚假尖锐边缘的人工分段常数块区域，称为阶梯效应。为了减少阶梯效应，同时保留全变差的边缘保留特性，对TV进行了高阶l1范数的改进 [6]。

TV正则化用可微函数近似TV可能会导致图像分辨率和对比度的损失，以及解的不稳定性。Li [7] 引入了一种基于接近算子的不动点算法，即前置条件交替投影算法(PAPA)，该算法严格地处理不可微TV正则化，提供了一种鲁棒有效的迭代方案，并且利用高阶TV (HOTV)正则化的方法实现了SPECT重建的算法PAPA-TV。

之后，Li用ICTV惩罚项 [8] 代替了重建模型 [7] 中的TV项，对所涉及的图像分量之和施加了非负性约束。此外，在图像质量评估方面，该研究考察了ICTV正则化处理楼梯伪影的能力，两个图像分量都是非负的，因为两个分量代表不同平滑度的图像区域，并且整个图像域的放射性分布是非负的。这产生了一个更合理的SPECT重构模型。

2.2. 下卷积正则项

重建模型F的定义：

$F\left(u\right)=\langle A\left(f_1+f_2\right),1\rangle -\langle \ln \left(A\left(f_1+f_2\right)+\gamma \right),g\rangle$ (1)

在论文 [2] 中，作者提出以下迭代模型来求F的最优解：

$\{\begin{array}{l}{h}^{\left(k\right)}=P_{+}\left(u^{\left(k\right)}-S\nabla \tilde{F}\left(u^{\left(k\right)}\right)-S{B}^{\text{T}}T{b}^{\left(k\right)}\right)\hfill \\ b^{\left(k+1\right)}=\left(I-{\mathrm{prox}}_{\phi }^T\right)\left(b^{\left(k\right)}+B{h}^{\left(k\right)}\right)\hfill \\ u^{\left(k+1\right)}=P_{+}\left(u^{\left(k\right)}-S\nabla \tilde{F}\left(u^{\left(k\right)}\right)-S{B}^{\text{T}}T{b}^{\left(k+1\right)}\right)\hfill \end{array}$ (2)

在迭代格式(2)中， $b\in {\text{R}}^{12d}$ 为双变量；S是一个2d*2d对角正定预处理矩阵，它加速合成算法， $T:=\text{diag}\left({\mu }_1{I}_{3d},{\mu }_2{I}_{9d}\right)$ 是一个带有正参数 ${\mu }_1$ 和 ${\mu }_2$ 的12d*12d对角矩阵。在原始PAPA的驱动下，我们选择预处理矩阵作为第k次迭代的对角矩阵 $S^{\left(k\right)}:=\mathrm{diag}\left(S_1^{\left(k\right)},S_2^{\left(k\right)}\right)$，其中 $S_1^{\left(k\right)}=\mathrm{diag}\left(f_1^{\left(k\right)}/A^{\text{T}}1\right)$， $S_2^{\left(k\right)}=\mathrm{diag}\left(f_2^{\left(k\right)}/A^{\text{T}}1\right)$。每次迭代的重建图像由 $f^{\left(k\right)}:=f_1^{\left(k\right)}+f_2^{\left(k\right)}$ 给出。

迭代模型(2)的实现也要求 ${\text{P}}_{+}$ 和 ${\mathrm{prox}}_{\phi }^{T^{-1}}$ 的闭集，算子 ${\text{P}}_{+}$ 是一个封闭集合 $\left\{y\in {\text{R}}^{2d}:y_i\ge 0,i=1,2,\cdots ,2d\right\}$ 的投影算子。对于 $x\in {\text{R}}^{2a}$，我们有 ${\left(P_{+}\left(x\right)\right)}_i=\max \left\{x_i,0\right\}$。对于ICTV正规项 $\phi \left(z\right)={\lambda }_1{\phi }_1\left(z_1\right)+{\lambda }_2{\phi }_2\left(z_2\right)$，其中 $z_1\in {\text{R}}^{3d}$， $z_2\in {\text{R}}^{9d}$，对应与向量1/4上部分和3/4下部分。我们可以看到函数u是可分为两个变量z₁和z₂。根据论文 [9]， $\phi$ 的proximity算子有这样的形式 ${\mathrm{prox}}_{\phi }^{T^{-1}}\left(z\right)=\left[\begin{array}{c}{\mathrm{prox}}_{\left({\lambda }_1/u_1\right){\phi }_1}\left(z_1\right)\\ {\mathrm{prox}}_{\left({\lambda }_2/u_2\right){\phi }_2}\left(z_2\right)\end{array}\right]$，计算 $\phi$ 的proximity算子相当于计算 ${\mathrm{prox}}_{\left({\lambda }_1/u_1\right)}\left(z_1\right)$ 和 ${\mathrm{prox}}_{\left({\lambda }_2/u_2\right)}\left(z_2\right)$，根据论文 [10]，对于向量 ${\text{y}}_1:={\mathrm{prox}}_{\left({\lambda }_1/u_1\right){\phi }_1}\left(z_1\right)$ 我们可以这样计算： ${\text{y}}_{2_i}={\left[y_{2_i},y_{2_{i+d}},\cdots ,y_{2_{i+8d}}\right]}^{\text{T}}$， $y_{1_i}=\max \left\{\Vert Z_{1_i}\Vert -\frac{{\lambda }_1}{{\mu }_1},0\right\}\frac{Z_{1_i}}{\Vert Z_1\Vert },i=1,2,\cdots ,d$，其中 $y_{1_i}={\left[y_{1_i},y_{1_{i+d}},y_{1_{i+2d}}\right]}^{\text{T}}$ 和 $Z_{1_i}={\left[z_{1_i},z_{1_{i+d}},z_{1_{i+2d}}\right]}^{\text{T}}$ 是两个3D向量。对于计算 ${\text{y}}_2:={\mathrm{prox}}_{\left({\lambda }_2/u_2\right){\phi }_2}\left(z_2\right)$，只需相应的用两个大小为9D的向量和 ${\text{z}}_{2_i}={\left[z_{2_i},z_{2_{i+d}},\cdots ,z_{2_{i+8d}}\right]}^{\text{T}}$ 代替上式中的 ${\text{y}}_1$ 和 ${\text{z}}_1$， ${\lambda }_1/u_1$ 与 ${\lambda }_2/u_2$ 同理。

对于带约束的ECT图像重建优化模型(1)，调用预处理交替投影算法对其进行求解，下卷积型二阶全变差正则化的图像重构优化模型：

${\min }_{f\in {ℝ}^d}\left\{\langle Af,1\rangle -\langle \ln \left(Af+\gamma \right),g\rangle +{\min }_{f=f_1+f_2}\left\{{\lambda }_1\phi \left(B_1{f}_1\right)+{\lambda }_2\psi \left(B_2{f}_2\right)\right\}\right\}$ (3)

该模型使用一阶全变差与二阶全变差的下卷积来惩罚数据拟合项。下卷积的定义：对于合适的凸函数 ${\psi }_i:R^n\to R\cup \left\{+\infty \right\},i=1,2,\cdots ,N,N\ge 2$，它的下卷积即 $\psi$ 定义为：

$\psi \left(f\right)=\left({\psi }_1\square \cdots \square {\psi }_N\right)\left(f\right):=\underset{f=f_1+\cdots +f_N}{\inf }{\displaystyle \underset{j=1}{\overset{N}{\sum }}{\psi }_i}\left(f_i\right)$ (4)

该正则化模型(1)把重构图像分解成两个部分，其中f₁适用于一阶全变差正则化，而f₂适用于二阶全变差正则化，这意味着对f₂的光滑性要求比f₁更高。因此,直观上来看，f₁着重刻画了重构图像中的细节以及边界信息，而f₂则倾向于刻画图像中的光滑区域。全变差的公式：

$U\left(Z\right)={\displaystyle \underset{i}{\sum }{\displaystyle \underset{j}{\sum }\sqrt{{\left({\nabla }_{i,j}^{h}Z\right)}^2+{\left({\nabla }_{i,j}^{v}Z\right)}^2}}}$ (5)

其中 ${\nabla }_{i,j}^{h}Z$ 表示水平方向的梯度， ${\nabla }_{i,j}^{v}Z$ 表示垂直方向的梯度。

3. 本文方法

对于小波，脊波、曲波、轮廓波等多尺度几何方法能够表达丰富变化的纹理细节，但是在频率空间中曲波和轮廓波是隔层细分的，这在一定程度上影响了其稀疏表示。剪切波(Shearlets) [11] 是多尺度几何分析的最新发展，它是K.H. Guo和G. Labate等通过特殊形式的具有合成膨胀的仿射系统构造的一种接近最优的多维函数稀疏表示法，对图像的表示同时具有多分辨、局域性和方向性等优点。剪切波变换不仅具有与曲线波和轮廓波相同的非线性误差逼近阶，而且在频率空间中是逐层细分的，所以具有更好的表示性能。与此同时，shearlet变换的数学结构比较简单，它通过对一个函数进行伸缩、平移、旋转来生成基函数，该特点与小波类似，却正是曲波和轮廓波所缺少的。本文用shearlet作为重建模型的正规项。当维数为2时，其仿射系统表示为具有合成膨胀的仿射变换系统，表达式为

$M_{\text{AH}}\left(\phi \right)={\phi }_{j,t,k}\left(x\right)={\left|\det A\right|}^{i/2}\phi {\left(B^i{A}^{j}x-k\right)}_{i}j,l\in Z,k$ (6)

式中基函数 ${\phi }_{j,t,k}\left(x\right)$ 的集合为通过对单个局部特性良好的窗函数进行平移、旋转、剪切操作而形成；矩阵A决定图像的多尺度分解，是具有各向异性的膨胀矩阵；矩阵B决定图像的多方向分解，是剪切矩阵； $\left|\det \text{A}\right|=1$ ；j为分解尺度l为方向参数；k为平移参数。当 $M_{\text{AH}}\left(\phi \right)$ 具有紧框架，则(6)式中的 ${\rho }_{j,t,k}\left(x\right)$ 为合成小波。剪切波中，A、B一般表示为：

$A=\left[\begin{array}{ll}4\hfill & 0\hfill \\ 0\hfill & 2\hfill \end{array}\right],B=\left[\begin{array}{ll}1\hfill & 1\hfill \\ 0\hfill & 1\hfill \end{array}\right]$

而在公式(5)中，它只有水平、垂直两个方向，不能很好地表达丰富变化的细节。而多尺度分析具有各向异性和方向性等特点，所以能够对图像中有很高各向异性的边缘和纹理等信息给出接近最优的表示。

把shearlet的滤波器来分成两组作为论文 [8] 中的SPECT重建模型(3)中的B1和B2惩罚项，优化模型同(1)。根据不同的尺度对应于不同的光滑度和对图像的表征来进行分组。利用3维剪切波系统(ShearLab 3D) 最优表达高维数据的能力对图像分解，所应用的剪切波变换系统有五个尺度。经实验，scale为0、1、2可刻画图像中的细节以及边界信息，而scale为3、4来刻画图像中的光滑区域，所以把该剪切波滤波器分为两部分，其中一组B1滤波器作用于f₁，另一组B2滤波器作用于f₂，该重建方法称为PAPA-ICSL。

4. 实验测试与结果分析

4.1. 实验数据

我们使用了Monte Carlo仿真软件包来获得扇形光束(焦距43.1 cm) SPECT仿真数据(由128 × 64尺寸检测器矩阵中的120个投影视图组成，具有3.56 mm检测器元件尺寸，和2.2毫米重建空间体素大小)分段常数幻影。我们模拟直径20.8厘米和长度为14.08厘米，含有均匀的冷、热且带有尖锐的边缘球体的均匀气缸：六个传动系统的平面，在与相对球体相同的径向距离，与背景活动比为2:1和中央横截面区域从0.58 cm²为球体为6至4.26 cm²的球体(图1)。将得到的蒙特卡罗模拟投影图像乘以适当的常数，得到120个视图中高噪声数据和低噪声数据的总数分别为4.2 × 106和8.4 × 106。

Figure 1. Transaxial cross-sections of a phantom: six hot Gaussian blobs

图1. 模体的轴位截面：六个高斯热斑点

4.2. 实验平台

本文中所有实验均采用Window 10操作系统，CPU为Intel Core i5-4200H，2.8 Ghz，内存8 g。使用MATLAB 2018a平台进行仿真实验。

4.3. 各项指标

4.3.1. 均方误差

我们使用均方误差(MSE)来评估重建的准确性。MSE是一种全局的图像质量度量，它量化了整个重建空间中重建图像和真图(ground truth)之间的均方差。

4.3.2. 峰值信噪比PSNR

峰值信噪比，是一个表示信号最大可能功率和影响它的表示精度的破坏性噪声功率的比值的工程术语。

4.3.3. 结构相似度

结构相似度(SSIM)从图像组成的角度将结构信息定义为独立于亮度、对比度的反映场景中物体结构的属性，并将失真建模为亮度、对比度和结构三个不同因素的组合。用均值作为亮度的估计，标准差作为对比度的估计，协方差作为结构相似程度的度量。

4.4. 实验结果

从实验结果表1可以看出，高噪声、低噪声的投影图像使用剪切波变换下卷积惩罚项(PAPA-ICSL)的重建图像其SSIM，PSNR，MSE均有所提升，说明重建图像跟接近原图；而由重建图像图2、图3可见，本文方法PAPA-ICSL的重建图像没有PAPA-TV，PAPA-ICTV的阶梯型伪影，这正是因为剪切波变换能表达图像多个方向的信息，通过两组剪切波变换构造的滤波器分别刻画图像的细节边界信息和光滑区域。

Table 1. Reconstruction results of hot spheres by different methods

表1. 不同方法对热球的重建结果

(a) PAPA-TV (b) PAPA-ICTV (c) PAPA-ICSL

Figure 2. Reconstructed images of high noise hot sphere obtained by three investigated methods

图2. 三种研究方法获得的高噪声热球的重建图像

(a) PAPA-TV (b) PAPA-ICTV (c) PAPA-ICSL

Figure 3. Reconstructed images of the low noise hot sphere obtained by three investigated methods

图3. 三种研究方法获得的低噪声热球的重建图像

从脑体模的重建结果图4可见，本文提出的方法PAPA-ICSL的重建图像相比PAPA-TV、PAPA-ICTV保留了更多的细节。

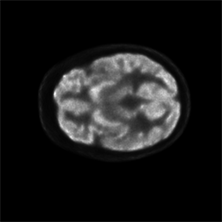(a) PAPA-TV 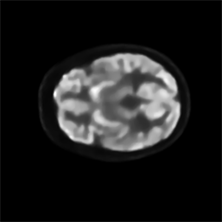(b) PAPA-ICTV (c) PAPA-ICSL

Figure 4. Reconstructed images of the denoised brain phantom obtained by three investigated methods

图4. 用三种方法对去噪的脑模体的重建结果

5. 结论

本文针对低剂量SPECT图像重建问题，提出了一种基于剪切波变换下卷积惩罚项的重建算法。实验表明：该算法在低剂量图像重建时，能够进一步消除阶梯状伪影，同时保留更多图像的细节，从而有效提高重建图像的质量。同时本文方法重建的图像中仍有一定程度的噪声，影响了重建的整体效果，需要在抑制噪声方面做进一步改进。