一类含时滞的氮–磷–浮游植物模型的动力学分析

Dynamic Analysis of a Nitrogen-Phosphorus-Phytoplankton Model with Delay

摘要: 本文构建了一类含时滞的氮–磷–浮游植物模型，对模型进行了理论分析和数值模拟。理论分析结果表明，时滞会导致模型正平衡点经由Hopf分支发生失稳，随后我们利用范数和中心流形定理证明了Hopf分支的分支方向及分支周期解的稳定性。数值模拟结果与理论结果一致，且结果表明浮游植物种群密度振幅与时滞参数呈正相关关系。本文结果有助于理解时滞对浮游植物吸收营养过程的影响。

Abstract: In this paper, we propose a nitrogen-phospho-phytoplankton model with time delay and the model is analyzed theoretically and numerically. The theoretical analysis shows that delay can destabilize the stability of the positive equilibrium of the model via Hopf bifurcation. Then we calculate the bifurcation direction of the Hopf bifurcation and the stability of the periodic solution by using norm form and central manifold theorem. The numerical simulation results are consistent with the theoretical analysis, and the results show that the amplitude of phytoplankton population density is positively correlated with the time delay parameters. Our results are helpful to understand the effect of time delay on the process of phytoplankton nutrient uptake.

1. 引言

浮游植物作为水生生态系统的基础，对水生生态的平衡及大气环境有重要影响。浮游植物能够吸收二氧化碳并产生氧气，且在全球碳循环过程中扮演重要角色。但藻类的过量增长会污染水质，导致水体发黑、发臭，严重影响水生生物健康，并且有些产毒藻类会产生毒素，通过食物链对人类健康造成威胁 [1]。近些年，藻类暴发已经成为全球关注的热点问题 [2]，尽管众多学者对藻类增长过程进行了研究，但由于藻类增长过程是高度非线性而且水生环境是非常复杂的，致使藻类增长过程的详细机制目前仍是不清楚，但是依然需提出更合理的解释。

实地观察和实验结果揭示了众多因子都会对藻类增长产生影响，比如：光照 [3]，温度 [4]，营养 [5]，捕食 [6] 等等。在众多影响因子中，高营养浓度和适宜的生长环境被认为是导致藻类暴发的主要因素 [7]。研究表明在大多数水生生态系统中，氮和磷是藻类生长的主要限制和影响因素 [8]。此外，大量研究还表明氮磷比也是影响藻类生长的重要因素。Smith等 [9] 通过分析17个湖的数据研究了氮磷比对浮游植物生长的影响，结果表明一些藻类偏爱生活在特定氮磷比的水体中。此外，文献 [10] 的研究表明了，单方面减低水体中的氮含量并不能减缓水体富营养化程度。显然，氮磷营养浓度在水体中的地位举足轻重。

众多研究表明藻类暴发是多种复杂过程相结合的结果，包括化学过程、生物过程和物理过程 [11]，并且水生生态系统的复杂性和高度非线性导致对藻类增长机制的研究变得非常困难。因此，数学模型为很多学者提供了可靠的研究方法，数学模型能够对藻类增长的动力学机制提供定量研究，为藻类增长过程中的重要机制提供新的认识 [12] [13] [14]。通常，人们在模型建立时，并未考虑浮游植物增长过程中存在的时滞效应，然而Caperon [15] 选用Isochrysis galbana对其生长过程进行了实验研究，发现时滞确实存在于Isochrysis galbana的增长过程中。此外，结果表明模型在研究时滞对浮游植物增长的影响过程中具有重要作用。因此在藻类增长模型建立中，时滞是非常重要的因素。

近年来，越来越多的证据表明含时滞的模型能够产生更加丰富的动力学性质，比如，时滞能够引发系统发生失稳，诱发稳态交替的产生，甚至产生由时滞诱发的混沌行为 [16] [17] [18] [19] [20]。文章 [21] 建立了一类具有时滞的营养–浮游植物模型，结果表明时滞能够通过Hopf分支诱发系统发生失稳，并且在特定条件下会产生稳态交替，而混沌行为也可能经由3-周期解产生。根据文献 [21] 的工作，本文我们建立了一类含有时滞的氮磷–浮游植物模型。特别地，时滞表示由于浮游植物吸收营养而产生的时间滞后性。建立模型如下：

$\{\begin{array}{l}\frac{\text{d}N}{\text{d}t}=I_1-q_{1}N-{\alpha }_{1}NA\\ \frac{\text{d}P}{\text{d}t}=I_2-q_{2}P-{\alpha }_{2}PA\\ \frac{\text{d}A}{\text{d}t}=\epsilon {\alpha }_1{\alpha }_{2}N\left(t-\tau \right)P\left(t-\tau \right)A^2-mA\end{array}$ (1)

其中N，P，A分别表示t时刻的氮含量，磷含量，浮游植物生物量； $I_1$ 和 $I_2$ 分别表示氮磷营养的输入； $q_1$， $q_2$ 分别表示氮和磷的流失率； ${\alpha }_1$ 表示浮游植物的氮营养盐吸收率， ${\alpha }_2$ 表示浮游植物对磷营养盐的吸收率； $\epsilon$ 是营养利用率，m是浮游植物死亡率， $\tau$ 表示浮游植物吸收营养产生的时滞参数。假设所有参数为正。本论文的主要工作是解析时滞对藻类增长的影响，探讨时滞如何影响藻类增长的动力学行为。

2. 模型正平衡点存在性

本文中，根据生物学意义，我们只考虑模型(1)的正平衡点。对模型(1)有 $N^{*}=\frac{I_1}{q_1+{\alpha }_1{A}^{*}}$， $P^{*}=\frac{I_2}{q_2+{\alpha }_2{A}^{*}}$，且 $A^{*}$ 是下面方程的对应的根：

$m{\alpha }_1{\alpha }_2{A}^{\ast }{}^{{}^2}+\left(m{q}_1{\alpha }_2+m{q}_2{\alpha }_1-\epsilon {\alpha }_1{\alpha }_2{I}_1{I}_2\right)A^{\ast }+m{q}_1{q}_2=0.$ (2)

定义方程 $f\left(A\right)=m{\alpha }_1{\alpha }_2{A}^2+\left(m{q}_1{\alpha }_2+m{q}_2{\alpha }_1-\epsilon {\alpha }_1{\alpha }_2{I}_1{I}_2\right)A+m{q}_1{q}_2$，显然有 $f\left(0\right)=m{q}_1{q}_2>0$。为了方便计算，记 $L=m{q}_1{\alpha }_2+m{q}_2{\alpha }_1-\epsilon {\alpha }_1{\alpha }_2{I}_1{I}_2$， $\Delta =L^2-4m^2{\alpha }_1{\alpha }_2{q}_1{q}_2$。当 $L<0$，则方程(2)有两个正根 $A_{\ast }^1$ 和 $A_{\ast }^2$ 当且仅当 $\Delta >0$，表明模型(1)在此时存在两个正根 $E_{\ast }^1=\left(N_{\ast }^1,P_{\ast }^1,A_{\ast }^1\right)$ 和 $E_{\ast }^2=\left(N_{\ast }^2,P_{\ast }^2,A_{\ast }^2\right)$，其中

$N_{\ast }^1=\frac{I_1}{q_1+{\alpha }_1{A}_{\ast }^1},P_{\ast }^1=\frac{I_2}{q_2+{\alpha }_2{A}_{\ast }^1},A_{\ast }^1=\frac{-L+\sqrt{\text{Δ}}}{2m{\alpha }_1{\alpha }_2};$

$N_{\ast }^2=\frac{I_1}{q_1+{\alpha }_1{A}_{\ast }^2},P^{\ast 2}=\frac{I_2}{q_2+{\alpha }_2{A}_{\ast }^2},A_{\ast }^2=\frac{-L-\sqrt{\text{Δ}}}{2m{\alpha }_1{\alpha }_2}.$

则可得下面定理：

定理2.1：对模型(1)，当 $L<0$ 和 $\text{Δ}>0$ 成立，则存在两个正平衡点，记为 $E_{\ast }^1$ 和 $E_{\ast }^2$。

3. 局部稳定性分析和Hopf分支

令 ${\hat{E}}^{*}=\left({\hat{N}}^{*},{\hat{P}}^{*},{\hat{A}}^{*}\right)$ 为定理2.1中任一正平衡点。首先将模型(1)平衡点移到原点，令 $u_1=N\left(t\right)-{\hat{N}}^{*}$， $u_2=P\left(t\right)-{\hat{P}}^{*}$， $u_3=A\left(t\right)-{\hat{A}}^{*}$，则模型(1)的线性形式如下：

$\{\begin{array}{l}{\stackrel{\dot{}}{u}}_1=a_{11}{u}_1\left(t\right)+a_{13}{u}_3\left(t\right)\\ {\stackrel{\dot{}}{u}}_2=a_{22}{u}_2\left(t\right)+a_{23}{u}_3\left(t\right)\\ {\stackrel{\dot{}}{u}}_3=a_{13}{u}_1\left(t-\tau \right)+a_{32}{u}_2\left(t-\tau \right)+a_{33}{u}_3\left(t\right)\end{array}$ (3)

其中：

$\begin{array}{l}{a}_{11}=-q_1-{\alpha }_1{\hat{A}}^{*};a_{13}=-{\alpha }_1{\hat{N}}^{*};\\ a_{22}=-q_2-{\alpha }_2{\hat{A}}^{*};a_{23}=-{\alpha }_2{\hat{P}}^{*};\\ a_{31}=\epsilon {\alpha }_1{\alpha }_2{\hat{P}}^{*}{\hat{A}}^{*}{}^{{}^2};a_{32}=\epsilon {\alpha }_1{\alpha }_2{\hat{N}}^{*}{\hat{A}}^{*}{}^{{}^2};a_{33}=2\epsilon {\alpha }_1{\alpha }_2{\hat{N}}^{*}{\hat{P}}^{*}{\hat{A}}^{*}-m\end{array}$ (4)

注意到当 ${\hat{E}}^{*}$ 存在时 $m=\epsilon {\alpha }_1{\alpha }_2{\hat{N}}^{*}{\hat{P}}^{*}{\hat{A}}^{*}$，有 $a_{33}=m$。则模型(3)对应的特征方程为

${\lambda }^3+B{\lambda }^2+C\lambda +\left(D+E\right)\lambda {\text{e}}^{-\lambda \tau }+\left(F+G\right){\text{e}}^{-\lambda \tau }+H=0,$ (5)

其中

$\begin{array}{l}B=-\left(a_{11}+a_{22}+a_{33}\right);C=a_{11}{a}_{22}+a_{11}{a}_{33}+a_{22}{a}_{33};D=-a_{13}{a}_{31};\\ E=-a_{23}{a}_{32};F=a_{13}{a}_{31}{a}_{22};G=a_{11}{a}_{23}{a}_{32};H=-a_{11}{a}_{22}{a}_{33}.\end{array}$ (6)

3.1. 正平衡点 $E_{\ast }^2$ 的稳定性

本小节，我们首先证明 $E_{\ast }^2$ 和 $E_{\ast }^1$ 的稳定性，且有如下结果：

定理 3.1：当模型(1)存在两个正平衡点，则 $E_{\ast }^2$ 始终是不稳定正平衡点。

证明：当 $\tau =0$ 时，方程(5)变为

${\lambda }^3+B{\lambda }^2+\left(C+D+E\right)\lambda +\left(F+G+H\right)=0,$ (7)

记 $A_1=C+D+E$， $A_2=F+G+H$，为了计算方便，我们仅估计 $A_2$ 的符号。由方程(4)和(6)，我们有

$\begin{array}{c}{A}_2\left({\hat{A}}^{*}{}^{{}^2}\right)=m\left({\alpha }_1{\alpha }_2{\hat{A}}^{*}{}^{{}^2}-q_1{q}_2\right)\\ =m\left(\frac{{\left(-L\pm \sqrt{\text{Δ}}\right)}^2}{4m^2{\alpha }_1{\alpha }_2}-q_1{q}_2\right)\\ =\frac{2\sqrt{\text{Δ}}\left(\sqrt{\text{Δ}}\mp L\right)}{4m{\alpha }_1{\alpha }_2},\end{array}$

由上述分析可知 $L<0$ 且 $0\le \sqrt{\Delta }<\left|L\right|$ 成立，显然有 $A_2\left(A_{\ast }^2\right)<0$，根据Routh-Hurwitz判据可得定理3.1。

3.2. 正平衡点 $E_{\ast }^1$ 的局部稳定性和Hopf分支

由小节3.1我们可得正平衡点 $E_{\ast }^2$ 始终是不稳定的，因此，在下文分析中，我们仅考虑正平衡点 $E_{\ast }^1$。

第一种情况： $\tau =0$。

当 $\tau =0$ 时方程(5)变为方程(7)如下

${\lambda }^3+B{\lambda }^2+\left(C+D+E\right)\lambda +\left(F+G+H\right)=0.$

显然可得正平衡点 $E_{\ast }^1$ 是局部渐近稳定的当且仅当 $B>0$， $C+D+E>0$， $F+G+H>0$ 成立。

第二种情况： $\tau >0$。

当 $\tau >0$ 时方程(5)变为

${\lambda }^3+B{\lambda }^2+C\lambda +\left(D+E\right)\lambda {\text{e}}^{-\lambda \tau }+\left(F+G\right){\text{e}}^{-\lambda \tau }+H=0.$ (8)

假定 $\lambda =i\omega \left(\omega >0\right)$ 是方程(8)的纯虚根，且分离实虚部可得

$\{\begin{array}{l}-{\omega }^3+C\omega =\left(F+G\right)\sin \left(\omega \tau \right)-\left(D+E\right)\omega \cos \left(\omega \tau \right),\\ -B{\omega }^2+H=-\left(F+G\right)\cos \left(\omega \tau \right)-\left(D+E\right)\omega \sin \left(\omega \tau \right),\end{array}$ (9)

对方程(9)两端平方相加可得下面方程：

${\omega }^6+U_1{\omega }^4+U_2{\omega }^2+U_3=0.$ (10)

其中

$U_1=B^2-2C,U_2=C^2-{\left(D+E\right)}^2-2BH,U_3=H^2-{\left(F+G\right)}^2.$

令 $v={\omega }^2$ 并且定义如下方程：

$f_3\left(v\right)=v^3+U_1{v}^2+U_{2}v+U_3$ (11)

显然 $U_3=\left(H+F+G\right)\cdot \left(H-F-G\right)$，根据方程(4)和(6)可得 $H-F-G<0$ 成立，且 $H+F+G=m\left({\alpha }_1{\alpha }_2{A}_{\ast }^1{}^{{}^2}-q_1{q}_2\right)$，由小节3.1可知 $H+F+G>0$ 成立。则可得 $U_3<0$，因此方程(11)有至少一个正根。不是一般性，记 $v_1,v_2,v_3$ 为方程(11)的根，则有 ${\omega }_k=\sqrt{v_k}$， $k=1,2,3$。

根据方程(9)可得时滞临界值如下：

${\tau }_k^j=\frac{1}{{\omega }_k}\left(\arccos \frac{\left(D+E\right){\omega }_k^4+\left[B\left(F+G\right)-C\left(D+E\right)\right]{\omega }_k^2-H\left(F+G\right)}{{\left(D+E\right)}^2{\omega }_k^2+{\left(F+G\right)}^2}+2\pi j\right),\left(j=0,1,2,\cdots ,k=1,2,3\right).$ (12)

令 ${\tau }_0={\min }_{k=1,2,3}{\tau }_k^0$，对方程(7)两端对 $\tau$ 进行微分可得

${\left(\frac{\text{d}\lambda }{\text{d}\tau }\right)}^{-1}=\frac{3{\lambda }^2+2B\lambda +C+\left(D+F\right){\text{e}}^{-\lambda \tau }}{\lambda \left[\left(D+F\right)\lambda +\left(E+G\right)\right]{\text{e}}^{-\lambda \tau }}-\frac{\tau }{\lambda },$ (13)

则可得：

$\mathrm{Re}{\left(\frac{\text{d}\lambda }{\text{d}\tau }\right)}_{\lambda =i{\omega }_0}^{-1}=\frac{{\omega }_0^2}{\Delta }{f^{\prime }}_3\left({\omega }_0^2\right),$ (14)

其中 $\text{Δ}={\left(-\left(D+E\right){\omega }_0^2\cos \left({\omega }_0\tau \right)+\left(F+G\right){\omega }_0\sin \left({\omega }_0\tau \right)\right)}^2+{\left(\left(F+G\right){\omega }_0\cos \left({\omega }_0\tau \right)+\left(D+E\right){\omega }_0^2\sin \left({\omega }_0\tau \right)\right)}^2$。当(H₁)： ${f^{\prime }}_3\left({\omega }_0^2\right)\ne 0$，则有 $\mathrm{Re}{\left(\text{d}\lambda /\text{d}\tau \right)}_{\lambda =i{\omega }_0}^{-1}\ne 0$ 成立，因此，我们有如下结论：

定理3.5：对模型(1)，当 $\tau >0$ 时，如果条件(H₁)成立，则正平衡点在区间 $\tau \in \left(0,{\tau }_0\right)$ 是局部渐近稳定的，且在 $\tau ={\tau }_0$ 时发生Hopf分支。

4. 分支性质

本节我们利用范数定理和中心流形定理 [22] 讨论Hopf分支的分支方向及分支周期解的稳定性。

定义 ${\omega }_0=\omega \left({\tau }_0\right)$，let $\tau ={\tau }_0+\mu$， $x\left(t\right)=N\left(\tau t\right)-N_{\ast }^1$， $y\left(t\right)=P\left(\tau t\right)-P_{\ast }^1$， $z\left(t\right)=A\left(\tau t\right)-A_{\ast }^1$。则模型(1)在 $C=C\left(\left[-1,0\right],R^3\right)$ 可重写为：

$\stackrel{\dot{}}{u}\left(t\right)=L\mu \left(u_t\right)+f\left(\mu ,u_t\right),$ (15)

其中 $u\left(t\right)={\left(x\left(t\right),y\left(t\right),z\left(t\right)\right)}^{\text{T}}\in R^3$， $u_t=u\left(t+\theta \right)$， $\theta \in \left[-1,0\right]$。 $L\mu \left(\phi \right):C\to R^3$ 和 $f\left(\mu ,u\left(t\right)\right)$ 表示如下：

$L_{\mu }\left(\phi \right)=\left(\tau +\mu \right)\left(A\phi \left(0\right)+B\phi \left(-1\right)\right),$

$f\left(\mu ,\phi \right)=\left(\tau +\mu \right){\left(f_1,f_2,f_3\right)}^{\text{T}},$

$A=\left(\begin{array}{ccc}{a}_{11}& 0& a_{13}\\ 0& a_{22}& a_{23}\\ 0& 0& a_{33}\end{array}\right),B=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ a_{31}& a_{32}& 0\end{array}\right),$

$f_1=-{\alpha }_1{\phi }_1\left(0\right){\phi }_3\left(0\right),$

$f_2=-{\alpha }_2{\phi }_2\left(0\right){\phi }_3\left(0\right),$

$\begin{array}{l}{f}_3=\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{}^{{}^2}{\phi }_1\left(-1\right){\phi }_2\left(-1\right)+2\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{P}_{\ast }^1{\phi }_1\left(-1\right){\phi }_3\left(0\right)\\ +2\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{N}_{\ast }^1{\phi }_2\left(-1\right){\phi }_3\left(0\right)+2\epsilon {\alpha }_1{\alpha }_2{N}_{\ast }^1{P}_{\ast }^1{\phi }_3{\left(0\right)}^2+\cdots \end{array}$

根据Riesz表示定理，对一个有界变量存在一个 $3\times 3$ 方程 $\eta \left(\theta ,\mu \right)$ 满足 $L_{\mu }\phi ={\displaystyle {\int }_{-1}^0\text{d}\eta \left(\theta ,\mu \right)\phi \left(\theta \right)}$，对 $\theta \in C\left(\left[-1,0\right],R^3\right)$ 有

$\eta \left(\theta ,\mu \right)=\left({\tau }_0+\mu \right)Av\left(\theta \right)-\left({\tau }_0+\mu )\right)Bv\left(\theta +1\right),$

其中v表示Dirac delta函数：

$v\left(\theta \right)=\{\begin{array}{l}0,\theta \ne 0,\\ 1,\theta =0.\end{array}$

对 $\phi \in C^1\left(\left[-1,0\right],R^3\right)$，定义

$\Gamma \left(\mu \right)\phi =\{\begin{array}{l}\frac{\text{d}\phi \left(\theta \right)}{\text{d}\theta },\theta \in \left[-1,0\right),\\ {\displaystyle {\int }_{-1}^0\text{d}\eta \left(\mu ,s\right)\cdot \phi }\left(s\right),\theta =0,\end{array}$

$R\left(\mu \right)\phi =\{\begin{array}{l}0,\theta \in \left[-1,0\right),\\ f\left(\mu ,\phi \right),\theta =0,\end{array}$

因此，模型(1)可写为

$\stackrel{\dot{}}{u}\left(t\right)=\Gamma \left(\mu \right)u_t+R\left(\mu \right)u_t,$

对 $\psi \in C^1\left(\left[0,1\right],{\left(R^3\right)}^{*}\right)$，定义 $\Gamma$ 的耦合算子 ${\Gamma }^{*}$ 如下：

${\Gamma }^{*}\psi \left(s\right)=\{\begin{array}{l}-\frac{\text{d}\psi \left(s\right)}{\text{d}s},s\in \left(0,1\right],\\ {\displaystyle {\int }_{-1}^0\text{d}{\eta }^{\text{T}}\left(t,0\right)\psi }\left(-t\right),s=0.\end{array}$

一个线性内积定义如下：

$\langle \psi \left(s\right),\phi \left(\theta \right)\rangle =\bar{\psi }\left(0\right)\phi \left(0\right)-{\displaystyle {\int }_{-1}^0{\displaystyle {\int }_{\xi =0}^{\theta }\bar{\psi }\left(\xi -\theta \right)\text{d}\eta \left(\theta \right)\phi \left(\xi \right)\text{d}\xi }},$ (16)

其中 $\eta \left(\theta \right)=\eta \left(\theta ,0\right)$。且由前面分析可知 $\pm i{\omega }_0{\tau }_0$ 是 $\Gamma \left(0\right)$ 和 ${\Gamma }^{*}\left(0\right)$ 的特征值。

选择 $q\left(\theta \right)={\left(1,q_2,q_3\right)}^{\text{T}}{\text{e}}^{i{\omega }_0{\tau }_0\theta }$ 是 $\Gamma \left(0\right)$ 关于特征值 $i{\omega }_0{\tau }_0$ 的特征向量， $q^{*}\left(s\right)=D\left(1,q_2^{*},q_3^{*}\right){\text{e}}^{i{\omega }_0{\tau }_{0}s}$ 是 ${\Gamma }^{*}\left(0\right)$ 关于特征值 $-i{\omega }_0{\tau }_0$ 的特征向量。由直接计算我们有

$q_2=\frac{a_{23}\left(i{\omega }_0-a_{11}\right)}{a_{13}\left(i{\omega }_0-a_{22}\right)};q_3=\frac{i{\omega }_0-a_{11}}{a_{13}};$

$q_2^{*}=\frac{a_{32}{\text{e}}^{-i{\omega }_0{\tau }_0}\left(a_{11}+i{\omega }_0\right)}{a_{31}{\text{e}}^{-i{\omega }_0{\tau }_0}\left(a_{22}+i{\omega }_0\right)};q_3^{*}=\frac{-\left(a_{11}+i{\omega }_0\right)}{a_{31}{\text{e}}^{-i{\omega }_0{\tau }_0}}.$

此外，根据方程(16)，可得

$\bar{D}=\frac{1}{1+q_2{\bar{q}}_2^{*}+q_3{\bar{q}}_3^{*}+{\bar{q}}_3^{*}{a}_{31}{\tau }_0{\text{e}}^{-i{\omega }_0{\tau }_0}+q_2{\bar{q}}_3^{*}{a}_{32}{\tau }_0{\text{e}}^{-i{\omega }_0{\tau }_0}},$

满足 $\langle q^{*}\left(s\right),q\left(\theta \right)\rangle =1$， $\langle q^{*}\left(s\right),\bar{q}\left(\theta \right)\rangle =0$ 成立。

根据文献 [23] 计算方法可得如下决定分支性质的相关参数：

$\begin{array}{c}{g}_{20}=2\bar{D}{\tau }_0(-{\alpha }_1{q}_3-{\alpha }_2{\bar{q}}_2^{*}{q}_2{q}_3+\epsilon {\alpha }_1{\alpha }_2{q}_2{\bar{q}}_3^{*}{A}_{\ast }^1{}^{{}^2}{\text{e}}^{-2i{\omega }_0{\tau }_0}+2\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{P}_{\ast }^1{q}_3{\bar{q}}_3^{*}{\text{e}}^{-i{\omega }_0{\tau }_0}\\ +2\epsilon {\alpha }_1{\alpha }_2{N}_{\ast }^1{A}_{\ast }^1{\bar{q}}_3^{*}{q}_2{q}_3{\text{e}}^{-i{\omega }_0{\tau }_0}+2\epsilon {\alpha }_1{\alpha }_2{\bar{q}}_3^{*}{N}_{\ast }^1{P}_{\ast }^1{q}_3^2),\end{array}$

$\begin{array}{c}{g}_{11}=\bar{D}{\tau }_0[-{\alpha }_1\left(q_3+{\bar{q}}_3\right)-{\alpha }_2{\bar{q}}_2^{*}\left(q_2{\bar{q}}_3+{\bar{q}}_2{q}_3\right)+\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{}^{{}^2}{\bar{q}}_3^{*}\left({\bar{q}}_2+q_2\right)+2\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{P}_{\ast }^1{\bar{q}}_3^{*}\left({\bar{q}}_3{\text{e}}^{-i{\omega }_0{\tau }_0}+q_3{\text{e}}^{i{\omega }_0{\tau }_0}\right)\\ +2\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{N}_{\ast }^1{\bar{q}}_3^{*}\left({\bar{q}}_2{q}_3{\text{e}}^{i{\omega }_0{\tau }_0}+{\bar{q}}_3{q}_2{\text{e}}^{-i{\omega }_0{\tau }_0}\right)+4\epsilon {\alpha }_1{\alpha }_2{q}_3{\bar{q}}_3{\bar{q}}_3^{*}{N}_{\ast }^1{P}_{\ast }^1],\end{array}$

$\begin{array}{c}{g}_{02}=2\bar{D}{\tau }_0(-{\alpha }_1{\bar{q}}_3-{\alpha }_2{\bar{q}}_2^{*}{\bar{q}}_3{\bar{q}}_2+\epsilon {\alpha }_1{\alpha }_2{\bar{q}}_2{\bar{q}}_3^{*}{A}_{\ast }^1{}^{{}^2}{\text{e}}^{2i{\omega }_0{\tau }_0}+2\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{P}_{\ast }^1{\bar{q}}_3^{*}{\bar{q}}_3{\text{e}}^{i{\omega }_0{\tau }_0}\\ +2\epsilon {\alpha }_1{\alpha }_2{N}_{\ast }^1{A}_{\ast }^1{\bar{q}}_3^{*}{\bar{q}}_3{\bar{q}}_2{\text{e}}^{i{\omega }_0{\tau }_0}+2\epsilon {\alpha }_1{\alpha }_2{N}_{\ast }^1{P}_{\ast }^1{\bar{q}}_3^2{\bar{q}}_3^{*}),\end{array}$

$\begin{array}{c}{g}_{21}=2\bar{D}{\tau }_0\{-{\alpha }_1\left[W_{11}^{\left(3\right)}\left(0\right)+\frac{1}{2}{W}_{20}^{\left(3\right)}\left(0\right)+\frac{1}{2}{\bar{q}}_3{W}_{20}^{\left(1\right)}\left(0\right)+q_3{W}_{11}^{\left(1\right)}\left(0\right)\right]\\ -{\alpha }_2{\bar{q}}_2^{*}\left[q_2{W}_{11}^{\left(3\right)}\left(0\right)+{\bar{q}}_2\frac{1}{2}{W}_{20}^{\left(3\right)}\left(0\right)+\frac{1}{2}{\bar{q}}_3{W}_{20}^{\left(2\right)}\left(0\right)+q_3{W}_{11}^{\left(2\right)}\left(0\right)\right]\\ +\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{}^{{}^2}{\bar{q}}_3^{*}({\text{e}}^{-i{\omega }_0{\tau }_0}{W}_{11}^{\left(2\right)}\left(-1\right)+\frac{1}{2}{\text{e}}^{i{\omega }_0{\tau }_0}{W}_{20}^{\left(2\right)}\left(-1\right)\\ +\frac{1}{2}{\bar{q}}_2{\text{e}}^{i{\omega }_0{\tau }_0}{W}_{20}^{\left(1\right)}\left(-1\right)+q_2{\text{e}}^{-i{\omega }_0{\tau }_0}{W}_{11}^{\left(1\right)}\left(-1\right))+2\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{P}_{\ast }^1{\bar{q}}_3^{*}(q_3{W}_{11}^{\left(1\right)}(\; -\; 1\; )\end{array}$

$\begin{array}{l}+{\bar{q}}_3{W}_{20}^{\left(1\right)}\left(-1\right)+\frac{1}{2}{\text{e}}^{i{\omega }_0{\tau }_0}{W}_{20}^{\left(3\right)}\left(0\right)+{\text{e}}^{-i{\omega }_0{\tau }_0}{W}_{11}^{\left(3\right)}\left(0\right))\\ +2\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{N}_{\ast }^1{\bar{q}}_3^{*}(q_3{W}_{11}^{\left(2\right)}\left(-1\right)+\frac{1}{2}{\bar{q}}_3{W}_{20}^{\left(2\right)}\left(-1\right)\\ +{\bar{q}}_2\frac{1}{2}{\text{e}}^{i{\omega }_0{\tau }_0}{W}_{20}^{\left(3\right)}\left(0\right)+q_2{\text{e}}^{-i{\omega }_0{\tau }_0}{W}_{11}^{\left(3\right)}\left(0\right))\\ \begin{array}{c}\\ \end{array}+2\epsilon {\alpha }_1{\alpha }_2{P}_{\ast }^1{N}_{\ast }^1{\bar{q}}_3^{*}\left({\bar{q}}_3{W}_{20}^{\left(3\right)}\left(0\right)+2q_3{W}_{11}^{\left(3\right)}\left(0\right)\right)\}\end{array}$

且

$W_{20}\left(\theta \right)=\frac{i{g}_{20}q\left(0\right)}{{\omega }_0{\tau }_0}{\text{e}}^{i\theta {\omega }_0{\tau }_0}+\frac{{\bar{g}}_{02}i}{3{\omega }_0{\tau }_0}\bar{q}\left(0\right){\text{e}}^{-i\theta {\omega }_0{\tau }_0}+E_1{\text{e}}^{2i\theta {\omega }_0{\tau }_0},$

$W_{11}\left(\theta \right)=\frac{-i{g}_{11}q\left(0\right)}{{\omega }_0{\tau }_0}{\text{e}}^{i\theta {\omega }_0{\tau }_0}+\frac{{\bar{g}}_{11}i}{{\omega }_0{\tau }_0}\bar{q}\left(0\right){\text{e}}^{-i\theta {\omega }_0{\tau }_0}+E_2,$

其中 $E_1$， $E_2$ 可分别用以下方程得到：

$\left(\begin{array}{ccc}2i{\omega }_0-a_{11}& 0& -a_{13}\\ 0& 2i{\omega }_0-a_{22}& -a_{23}\\ -a_{31}{\text{e}}^{-2i{\omega }_0{\tau }_0}& -a_{32}{\text{e}}^{-2i{\omega }_0{\tau }_0}& 2i{\omega }_0\end{array}\right)\cdot E_1=2\left(\begin{array}{c}{K}_{11}\\ K_{21}\\ K_{31}\end{array}\right),$

$\left(\begin{array}{ccc}{a}_{11}& 0& a_{13}\\ 0& a_{22}& a_{23}\\ a_{31}& a_{32}& 0\end{array}\right)\cdot E_2=-\left(\begin{array}{c}{K}_{12}\\ K_{22}\\ K_{32}\end{array}\right),$

其中，

$K_{11}=-{\alpha }_1{q}_3;K_{21}=-{\alpha }_2{q}_2{q}_3;$

$\begin{array}{l}{K}_{31}=\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{}^{{}^2}{q}_2{\text{e}}^{-2i{\omega }_0{\tau }_0}+2\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{P}_{\ast }^1{q}_3{\text{e}}^{-i{\omega }_0{\tau }_0}\\ +2\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{N}_{\ast }^1{q}_2{q}_3{\text{e}}^{-i{\omega }_0{\tau }_0}+2\epsilon {\alpha }_1{\alpha }_2{N}_{\ast }^1{P}_{\ast }^1{q}_3^2;\end{array}$

$K_{12}=-{\alpha }_1\left(q_3+{\bar{q}}_3\right);K_{22}=-{\alpha }_2\left(q_2{\bar{q}}_3+{\bar{q}}_2{q}_3\right);$

$\begin{array}{c}{K}_{32}=\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{}^{{}^2}\left({\bar{q}}_2+q_2\right)+4\epsilon {\alpha }_1{\alpha }_2{N}_{\ast }^1{P}_{\ast }^1\left(q_3{\bar{q}}_3\right)+2\epsilon {\alpha }_1{\alpha }_2{A}_{\ast }^1{P}_{\ast }^1\left(q_3{e}^{i{\omega }_0{\tau }_0}+{\bar{q}}_3{\text{e}}^{-i{\omega }_0{\tau }_0}\right)\\ +2\epsilon {\alpha }_1{\alpha }_2{N}_{\ast }^1{A}_{\ast }^1\left(q_3{\bar{q}}_2{\text{e}}^{i{\omega }_0{\tau }_0}+{\bar{q}}_3{q}_2{\text{e}}^{-i{\omega }_0{\tau }_0}\right).\end{array}$

显然， $g_{21}$ 可通过参数得到。则可计算下列值：

$c_1\left(0\right)=\frac{i}{2{\omega }_0{\tau }_0}\left(g_{20}{g}_{11}-2{\left|g_{11}\right|}^2-\frac{{\left|g_{02}\right|}^2}{3}\right)+\frac{g_{21}}{2},$

$\mu =-\frac{\mathrm{Re}\left(c_1\left(0\right)\right)}{\mathrm{Re}{\lambda }^{\prime }\left({\tau }_{20}^{*}\right)},$

$\beta =\mathrm{Re}\left(c_1\left(0\right)\right),$

$T=-\frac{\mathrm{Im}\left\{c_1\left(0\right)\right\}+{\mu }_2\mathrm{Im}\left\{{\lambda }^{\prime }\left({\tau }_0\right)\right\}}{{\omega }_0{\tau }_0}.$

进而可决定在 $\tau ={\tau }_0$ 处Hopf分支及分支周期解的性质如下：

1) $\mu$ 决定了Hopf分支的分支方向。特别地，当 $\mu >0\left(<0\right)$ 时，Hopf分支是超临界的(亚临界的)。

2) $\beta$ 决定了分支周期解的稳定性。当 $\beta <0\left(>0\right)$ 时，周期解是稳定的(不稳定的)。

3) T决定了分支周期解的周期。当 $T>0\left(<0\right)$ 时，分支周期解的周期是增加的(减小的)。

5. 数值模拟

本节我们将利用数值模拟对模型(1)的动力学行为做进一步分析。首先模型参数选择如下：

$I_1=2,I_2=2,q_1=0.01,q_2=0.01,{\alpha }_1=0.5,{\alpha }_2=0.05,\epsilon =0.1,$

选取浮游植物死亡率m和时滞参数 $\tau$ 为控制参数，初始值为 $\left(1,10,3\right)$。首先我们确定了时滞临界值随参数m的变化情况，如图1所示。图1结果表明当浮游植物死亡率在特定范围内时，时滞参数的临界值随浮游植物死亡率的增大而减小。

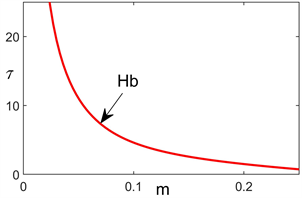
Figure 1. The critical value of delay in m-τ plane

图1. 在m-τ平面的时滞临界值

随后，我们选取浮游植物死亡率 $m=0.15$，根据方程(13)得到模型发生失稳的临界值为2.57。图2给出了不同时滞参数值下的时序图和相图。显然，当时滞参数值小于临界值时，模型(1)是局部渐近稳定的。但当时滞参数值大于临界值时，模型经由Hopf分支发生失稳，意味着营养–浮游植物震荡出现。值得注意的是，图2结果表明时滞参数值与浮游植物种群震荡强度之间呈现正相关关系，即时滞参数值的增加会加强浮游植物种群的震荡强度。

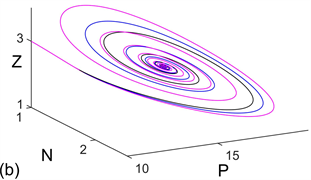
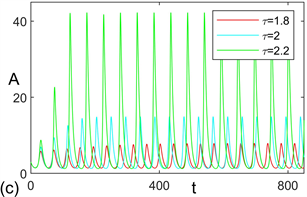
Figure 2. For model (1), (a) time series and (b) phase diagram with respect to $\tau =1.8,2.0,2.2$ ; (c) time series and (d) phase diagram with respect to $\tau =2.6,2.7,2.8$. Where black line, blue line, and magenta line represent $\tau =1.8,2.0,2.2$, respectively; red line, cayenne line, and green line represent $\tau =2.6,2.7,2.8$, respectively

图2. 对模型(1)，(a) $\tau =1.8,2.0,2.2$ 时的时序图；(b) $\tau =1.8,2.0,2.2$ 时的相图；(c) $\tau =2.6,2.7,2.8$ 时的时序图；(d) $\tau =2.6,2.7,2.8$ 时的相图。其中，黑色线，蓝色线，品红色线分别表示 $\tau =1.8,2.0,2.2$，红色线，卡宴色线，绿色线分别表示 $\tau =2.6,2.7,2.8$

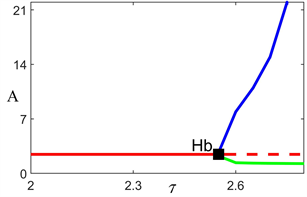
Figure 3. Bifurcation diagram of model (1)

图3. 模型(1)的分支图

由上述分析可知，当时滞 $\tau$ 取值增加时，正平衡点会经由Hopf分支发生失稳。为了进一步说明正平衡点稳定性关于时滞参数的变化，图3给出了模型(1)中浮游植物种群密度关于时滞 $\tau$ 的分支图。结果表明，当时滞超过临界值时正平衡点发生失稳，且浮游植物种群振幅与时滞参数值呈正相关关系，其结果与图2结果一致。

6. 结论

本文构建了一类含时滞的氮–磷–浮游植物模型，对模型平衡点稳定性及Hopf分支的存在性进行了分析，并对分支性质进行了计算。理论分析表明时滞能够诱发正平衡点发生失稳，即当时滞参数值大于临界值时，种群密度不会维持在一个特定值，而是发生震荡行为。随后，利用数值模拟对本文理论分析结果进行了进一步研究，数值模拟结果表明时滞能够诱发系统发生失稳，且浮游植物种群振幅与时滞参数值呈正相关关系。本文虽然不能准确描述水生生态系统中浮游植物的变化规律，但有助于理解时滞因素对浮游植物的营养吸收过程的影响。

致谢

首先，我要感谢我的导师赵敏教授，感谢他在我论文研究过程中给予的帮助和指导，在此表示由衷的谢意！

其次，感谢实验室的于恒国师兄和戴传军师兄，以及实验室的师兄师姐师弟师妹对我一直以来的帮助和鼓励，使我对科研有了更加浓厚的兴趣。

最后，由衷感谢温州大学数理学院的各位老师和领导，感谢他们的教导和帮助。同时感谢赵敏导师国家自然科学基金面上项目(61871293)的资助。