加性乘积风险率模型在聚类失效时间数据中的应用

Application of Additive Multiplicative Hazard Rate Model in Clustered Failure Time Data

摘要: 论文对聚类失效时间数据建立了加性–乘积风险率函数模型，根据模型创建了估计方程，应用牛顿迭代法求得参数向量的估计，并给出估计量的相合性和渐近正态性的证明。通过数值模拟验证了估计量在有限样本下的表现，最后分析了慢性肉芽肿病风险率函数的影响因素和因素的影响方式。

Abstract: In this paper, an additive multiplicative hazard rate function model is established for clustered failure time data, an estimation equation is created according to the model, the estimation of parameter vector is obtained by Newton iterative method, and the consistency and asymptotic normality of estimators are proved. The performance of the estimator under limited samples is verified by numerical simulation. Finally, the influencing factors and ways of the hazard rate function of chronic granulomatosis are analyzed.

1. 引言

生存分析在生物医学，工程中应用广泛。比如我们经常关心患某种疾病的病人的生存时间，工业产品的使用寿命，以及广义的生存时间，如某个感兴趣事件发生的时间。生存时间研究方法有非参数分析，参数分析方法和半参数分析方法。半参数分析方法的灵活性，稳健性和有效性介于其它两种方法之间，所以是最常用的一种方法。在生存分析数据的收集中，常常会遇到聚类数据，也就是个体之间不是完全独立的。比如数据是来自于各个医疗中心，或者是以家庭为单位收集的，还有的数据是一个个体的事件的重复发生。来自同一医疗中心的个案或同一家庭的个案或同一个体的多次复发数据，叫做成簇数据或聚类数据。同一个聚类的数据是有关系的，不同的类之间相互独立。

聚类失效时间的研究方法有边际建模方法和混合效应建模方法。在边际建模中，对同一个类的每个个体建立边际模型，建模时，对个体之间的关系不作任何假定，而在模拟部分，对同一类内个体间的关系进行一些假定 [1] [2] [3]。在混合效应模型中，对同一类的个体用一个共同的脆弱变量来说明个体之间的相关性 [4] [5]。以上文献大部分围绕着Cox模型 [6] 和加性风险模型。实际上加性乘积模型具有更强的灵活性。文献 [7] 提出一个广义加性乘积风险模型，以后的学者在此基础上进行进一步推广。文献 [8] 对带有辅助生存信息的加性乘积模型进行了统计推断。文献 [9] 对复发事件和终止事件进行联合分析，假设终止事件的风险率函数服从加性乘积模型。

加性乘积模型在聚类失效时间中的应用比较少，这篇论文是将加性乘积模型应用到聚类失效时间中。分析影响慢性肉芽肿病风险率函数的因素，以及影响方式。论文第一部分介绍了模型形式，估计方法和渐近理论证明，第二部分进行了数值模拟，验证提出的方法，第三部分对实际数据进行分析，第四部分是论文的总结和展望。

2. 模型和估计过程

2.1. 模型

首先把全部对象根据某个属性聚成n个簇。设第i个类中有 $n_i$ 个对象，其中 $i=1,2,\cdots ,n$，并用 $T_{ij}$ 表示第i个簇中第j个对象的失效时间， $C_{ij}$ 为右删失时间， $X_{ij}=\min \left(T_{ij},C_{ij}\right)$ 表示观察到的生存时间， ${\delta }_{ij}=I\left(T_{ij}\le C_{ij}\right)$ 表示第i类中第j个对象是否删失， $Z_{ij}$， $W_{ij}$ 为协变量向量。 $\tau$ 表示试验终止时间。

$T_{ij}$ 的风险率函数的定义如下：

${\lambda }_{ij}\left(t\right)={\lim }_{\Delta t\to 0}\frac{P\left(t\le T_{ij}<t+\Delta t|T_{ij}\ge t\right)}{\Delta t}$

对风险率函数 ${\lambda }_{ij}\left(t\right)$ 建立加性乘积模型，给定协变量 $Z_{ij}$， $W_{ij}$ 的情况下，假设风险率函数满足：

${\lambda }_{ij}\left(t|Z_{ij},W_{ij}\right)={\lambda }_0\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}{\beta }_0}+W_{ij}^{\text{T}}{\gamma }_0$ (1)

式中： ${\lambda }_0\left(t\right)$ 是基准风险率函数； ${\beta }_0$ 是协变量 $Z_{ij}$ 的效应，表示对风险率函数的乘积效应； ${\gamma }_0$ 是是协变量 $W_{ij}$ 的效应，表示对风险率函数的加性效应。

2.2. 模型估计过程

引入潜在的计数过程 $N_{ij}^{*}\left(t\right)=I\left(T_{ij}\le t\right)$ 和观测到的计数过程 $N_{ij}\left(t\right)={\delta }_{ij}I\left(T_{ij}\le t\right)$ 以及风险过程 $Y_{ij}\left(t\right)=I\left(T_{ij}>t\right){\delta }_{ij}$，根据风险率函数模型和计数过程的定义，得

$E\left(\text{d}{N}_{ij}\left(t\right)|Z_{ij},W_{ij}\right)=Y_{ij}\left(t\right)\left({\lambda }_0\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}{\beta }_0}+W_{ij}^{\text{T}}{\gamma }_0\right)\text{d}t$

进一步得到以下的零均值过程： $\text{d}{M}_{ij}\left(t\right)=\text{d}{N}_{ij}\left(t\right)-Y_{ij}\left(t\right)\left[{\lambda }_0\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}{\beta }_0}+W_{ij}^{\text{T}}{\gamma }_0\right]\text{d}t$。

根据文献 [10] 中的广义估计方程的思想，我们建立以下的估计方程：

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{\displaystyle {\int }_0^t\text{d}{N}_{ij}\left(u\right)}-Y_{ij}\left(u\right)\left[{\lambda }_0\left(u\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }+W_{ij}^{\text{T}}\gamma \right]\text{d}u}}=0$ (1)

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{\displaystyle {\int }_0^{\tau }{Z}_{ij}}\left[\text{d}{N}_{ij}\left(t\right)-Y_{ij}\left(t\right)\left[{\lambda }_0\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }+W_{ij}^{\text{T}}\gamma \right]\text{d}t\right]}}=0$ (2)

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{\displaystyle {\int }_0^{\tau }{W}_{ij}}\left[\text{d}{N}_{ij}\left(t\right)-Y_{ij}\left(t\right)\left[{\lambda }_0\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }+W_{ij}^{\text{T}}\gamma \right]\text{d}t\right]}}=0$ (3)

由(1)式可得：

${\Lambda }_0\left(t\right)={\displaystyle {\int }_0^t{\lambda }_0\left(u\right)\text{d}u}={\displaystyle {\int }_0^t\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\text{d}{N}_{ij}\left(u\right)-Y_{ij}\left(u\right)W_{ij}^{\text{T}}\gamma \text{d}u}}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{Y}_{ij}\left(u\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }}}}}$，

将 ${\Lambda }_0\left(t\right)$ 代入式(2)进一步计算得

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\underset{0}{\overset{\tau }{{\displaystyle \int }}}\left(Z_{ij}-\bar{Z}\right)\left(\text{d}{N}_{ij}\left(t\right)-Y_{ij}\left(t\right)W_{ij}^{\text{T}}\gamma \text{d}t\right)}}=0$ (4)

其中 $\bar{Z}=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{Z}_{ij}{Y}_{ij}\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }}}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{Y}_{ij}\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }}}}$。

将 ${\Lambda }_0\left(t\right)$ 代入式(3)进一步计算得

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\underset{0}{\overset{\tau }{{\displaystyle \int }}}\left(W_{ij}-\bar{W}\right)\left(\text{d}{N}_{ij}\left(t\right)-Y_{ij}\left(t\right)W_{ij}^{\text{T}}\gamma \text{d}t\right)}}=0$ (5)

其中 $\bar{W}=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{W}_{ij}{Y}_{ij}\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }}}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{Y}_{ij}\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }}}}$。

接下来，我们应用牛顿迭代法，对方程(4)和(5)进行求解，得到 $\beta ,\gamma$ 的估计。应用牛顿迭代法时，需要求出方程(4)和(5)左边表达式对 $\beta ,\gamma$ 的导函数。记：方程(4)的左边表达式为 $U_1\left(\beta ,\gamma \right)$，方程(5)的左边表达式为 $U_2\left(\beta ,\gamma \right)$。

$\begin{array}{c}\frac{\partial U_1\left(\beta ,\gamma \right)}{\partial {\beta }^T}=-{\displaystyle {\int }_0^{\tau }\left(\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{Z}_{ij}{Z}_{ij}^{\text{T}}{Y}_{ij}{\text{e}}^{Z_{ij}^{\text{T}}\beta }}}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{Y}_{ij}\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }}}}-\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{Z}_{ij}{Y}_{ij}\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{Z}_{ij}^{\text{T}}{Y}_{ij}\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}}\beta }}}}}{{\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{Y}_{ij}\left(t\right){\text{e}}^{Z_{ij}^T\beta }}}\right)}^2}\right){\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\left(Y_{ij}\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }{\lambda }_0\left(t\right)\text{d}t\right)}}}\\ =-{\displaystyle {\int }_0^{\tau }{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{Z}_{ij}{Y}_{ij}\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }}}}{\left(Z_{ij}-\bar{Z}\right)}^{\text{T}}{\lambda }_0\left(t\right)\text{d}t+o_p\left(n\right)\\ =-{\displaystyle {\int }_0^{\tau }{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\left(Z_{ij}-\bar{Z}\right)Y_{ij}\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }{Z}_{ij}^{\text{T}}{\lambda }_0\left(t\right)\text{d}t}}}+o_p(\; n\; )\end{array}$

类似的，可以计算出： $\frac{\partial U_1\left(\beta ,\gamma \right)}{\partial {\gamma }^T}=-{\displaystyle {\int }_0^{\tau }{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\left(Z_{ij}-\bar{Z}\right)Y_{ij}{W}_{ij}^{\text{T}}\text{d}t}}}$，

$\frac{\partial U_2\left(\beta ,\gamma \right)}{\partial {\beta }^T}=-{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{\displaystyle {\int }_0^{\tau }\left(W_{ij}-\bar{W}\right)Y_{ij}\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }{Z}_{ij}^{\text{T}}{\lambda }_0\left(t\right)\text{d}t+o_p(\; n\; )}}}$

$\frac{\partial U_2\left(\beta ,\gamma \right)}{\partial {\gamma }^T}=-{\displaystyle {\int }_0^{\tau }{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\left(W_{ij}-\bar{W}\right)Y_{ij}{W}_{ij}^{\text{T}}\text{d}t}}}$

把这四项写成矩阵形式，并记： $\hat{A}=\left(\begin{array}{c}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{\displaystyle {\int }_0^{\tau }\left(Z_{ij}-\bar{Z}\right)Y_{ij}\left(t\right)\left({\text{e}}^{Z_{ij}^{\text{T}}\beta }{Z}_{ij}^{\text{T}}{\lambda }_0\left(t\right)\text{d}t,W_{ij}^{\text{T}}\text{d}t\right)}}}\\ {\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{\displaystyle {\int }_0^{\tau }\left(W_{ij}-\bar{W}\right)Y_{ij}\left(t\right)\left({\text{e}}^{Z_{ij}^{\text{T}}\beta }{Z}_{ij}^{\text{T}}{\lambda }_0\left(t\right)\text{d}t,W_{ij}^{\text{T}}\text{d}t\right)}}}\end{array}\right)$

其中 $\theta ={\left({\beta }^{\text{T}},{\gamma }^{\text{T}}\right)}^{\text{T}}=\left(\begin{array}{c}\beta \\ \gamma \end{array}\right)$，

${\theta }_{\text{0}}={\left({\beta }_0^{\text{T}},{\gamma }_0^{\text{T}}\right)}^{\text{T}}=\left(\begin{array}{c}{\beta }_{\text{0}}\\ {\gamma }_{\text{0}}\end{array}\right)$，

$A\left(\theta \right)=-E\left\{{\displaystyle {\int }_0^{\tau }\left(\begin{array}{c}{Z}_{ij}-\bar{z}\\ W_{ij}-\bar{w}\end{array}\right)}\left({\text{e}}^{Z_{ij}^{\text{T}}\beta }{Z}_{ij}^{\text{T}}{\lambda }_0\left(t\right)\text{d}t,W_{ij}^{\text{T}}\text{d}t\right)Y_{ij}\left(t\right)\right\}$

其中 $\bar{z},\bar{w}$ 是 $\bar{Z},\bar{W}$ 的极限，由大数定律可知 $\frac{1}{n}\hat{A}\left(\theta \right)\stackrel{p}{\to }A\left(\theta \right)$。

2.3. 估计量的渐近性质

首先给出一些正则条件。

(C1) 协变量 $Z_{ij},W_{ij},j=1,2,\cdots ,n_i;i=1,\cdots ,n$.是有界的；

(C2) n组观测 $\left\{Z_{ij},W_{ij},T_{ij}\wedge C_{ij},{\delta }_{ij},Y_{ij}(\cdot ),N_{ij}(\cdot ),j=1,\cdots ,n_i\right\}$， $i=1,\cdots ,n$.是相互独立的；

(C3) $A\left(\theta \right)$ 在 ${\theta }_0$ 的邻域 H 上可逆。

定理1：在以上正则条件下，方程(4)，(5)的解在 ${\theta }_0$ 邻域 H 内存在且唯一，将这个解记作： $\hat{\theta }=\left(\begin{array}{c}\hat{\beta }\\ \hat{\gamma }\end{array}\right)$，且 $\hat{\theta }$ 是 ${\theta }_0$ 的相和估计。

证明：记

$\text{d}{M}_{ij}\left(t\right)=\text{d}{N}_{ij}\left(t\right)-Y_{ij}\left(t\right)\left({\lambda }_0\left(t\right)\exp \left(Z_{ij}^{\text{T}}\beta \right)+W_{ij}^{\text{T}}\gamma \right)\text{d}t$，

$U\left(\theta \right)=\left(\begin{array}{c}{U}_1\left(\theta \right)\\ U_2\left(\theta \right)\end{array}\right)=\left(\begin{array}{c}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{\displaystyle {\int }_0^{\tau }\left(Z_{ij}-\bar{Z}\right)\text{d}{M}_{ij}\left(t\right)}}}\\ {\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}{\displaystyle {\int }_0^{\tau }\left(W_{ij}-\bar{W}\right)\text{d}{M}_{ij}\left(t\right)}}}\end{array}\right)$。

可以证明 $\frac{1}{n}U\left({\theta }_0\stackrel{p}{\to }0\right)$。由于 $\frac{\partial \frac{1}{n}U\left(\theta \right)}{\partial {\theta }^{\text{T}}}=\frac{1}{n}\hat{A}\left(\theta \right)$，再根据大数定律，以及 $\hat{A}\left(\theta \right)$ 关于 $\theta$ 的连续性，可知在 ${\theta }_0$ 邻域内， $\frac{1}{n}\hat{A}\left(\theta \right)$ 依概率一致收敛到 $A\left(\theta \right)$，由假设： $A\left(\theta \right)$ 在 ${\theta }_0$ 邻域内可逆，这样当n充分大的时候， $\frac{1}{n}\hat{A}\left(\theta \right)$ 在 ${\theta }_0$ 邻域内可逆。由逆函数定理(Rudin, 1976) [11]，可以证明 $U\left(\theta \right)$ 在 ${\theta }_0$ 邻域内存在唯一解 $\hat{\theta }$。再由中值定理，在 ${\theta }_0$ 邻域内存在一个点 ${\theta }^{\text{*}}$ 使得， $\frac{1}{n}U\left(\hat{\theta }\right)-\frac{1}{n}U\left({\theta }_0\right)=\frac{1}{n}A\left({\theta }^{\text{*}}\right)\left(\hat{\theta }-{\theta }_0\right)$，当n充分大时，等号左边依概率收敛于0，等号右边的 $\frac{1}{n}A\left({\theta }^{\text{*}}\right)$ 可逆，因此当n充分大时 $\hat{\theta }\stackrel{p}{\to }{\theta }_0$。

定理2：在正则条件下 $\hat{\theta }$ 渐近服从 $\left(p+q\right)$ 维的正态分布， $\sqrt{n}\left(\hat{\theta }-{\theta }_0\right)$ 渐近服从 $N_{p+q}\left(0,\Sigma \right)$，其中

$\Sigma =A^{-1}\left({\theta }_0\right)E\left({\xi }_i^{\otimes 2}\right)A^{-1}{\left({\theta }_0\right)}^{\text{T}}$。

证明：根据函数中值定理，有

$\frac{1}{\sqrt{n}}U\left(\hat{\theta }\right)-\frac{1}{\sqrt{n}}U\left({\theta }_0\right)=\frac{1}{n}\hat{A}\left({\theta }_0\right)\left(\sqrt{n}\left(\hat{\theta }-{\theta }_0\right)\right)+O_p\left(1\right)$， $\sqrt{n}\left(\hat{\theta }-{\theta }_0\right)=-{\left(\frac{1}{n}\hat{A}\left({\theta }_0\right)\right)}^{{}^{-1}}\frac{1}{\sqrt{n}}U\left({\theta }_0\right)+O_p\left(1\right)$，

因为

$U\left({\theta }_0\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\left(\begin{array}{c}{\displaystyle {\int }_0^{\tau }\left(Z_{ij}-\bar{Z}\right)\text{d}{M}_{ij}\left(t\right)}\\ {\displaystyle {\int }_0^{\tau }\left(W_{ij}-\bar{W}\right)\text{d}{M}_{ij}\left(t\right)}\end{array}\right)}}\stackrel{记作}{\text{=}}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\xi }_i}+O_p\left(\sqrt{n}\right)$，

其中， ${\xi }_i={\displaystyle \underset{j=1}{\overset{n_i}{\sum }}\left(\begin{array}{l}{\displaystyle {\int }_0^{\tau }\left(Z_{ij}-\bar{z}\right)\text{d}{M}_{ij}\left(t\right)}\\ {\displaystyle {\int }_0^{\tau }\left(W_{ij}-\bar{w}\right)\text{d}{M}_{ij}\left(t\right)}\end{array}\right)}$ 是均值为0的随机变量，而且 ${\xi }_1,{\xi }_2,\cdots ,{\xi }_n$ 相互独立。所以由中心极限定理 $U\left({\theta }_0\right)$ 渐近服从正态分布 $N_{p+q}\left(0,nE\left({\xi }_i^{\otimes 2}\right)\right)$。前面已有 $\sqrt{n}\left(\hat{\theta }-{\theta }_0\right)=-\sqrt{n}{\hat{A}}^{-1}\left({\theta }_0\right)U\left({\theta }_0\right)+O_p\left(1\right)$ 再结合 $\frac{1}{n}\hat{A}\left({\theta }_0\right)\stackrel{p}{\to }A\left({\theta }_0\right)$，可得 $\sqrt{n}\left(\hat{\theta }-{\theta }_0\right)$ 渐近服从多元正态分布 $N_{p+q}\left(0,A^{-1}\left({\theta }_0\right)E\left({\xi }_i^{\otimes 2}\right)A^{-1}{\left({\theta }_0\right)}^{\text{T}}\right)$。

3. 数值模拟

首先，生成 $n\left(n=100,200,400\right)$ 个独立的类，每一个类的大小为2。协变量为 $Z_{ij}$ 和 $W_{ij}$ 分别服从参数为0.5的二项分布和区间(0, 1)的均匀分布，设失效时间的风险率函数模型为 ${\lambda }_{ij}\left(t|Z_{ij},W_{ij}\right)={\lambda }_0\left(t\right){\text{e}}^{\left(Z_{ij}^{\text{T}}{\beta }_0\right)}+W_{ij}^{\text{T}}{\gamma }_0$，设 ${\lambda }_0\left(t\right)=0.5$， $\left({\beta }_0,{\gamma }_0\right)$ 分别取(0.5, 0.5)，(1, 0.5)，(0.5, 1)。取试验截止时间为τ = 2，删失时间C取区间(0, v)上的均匀分布，v可以变化使得删失控制在30%~70%之间。首先生成基准失效时间 $T_{ij0}=-\log \left(1-\Phi \left(A_i+B_{ij}\right)\right)$，其中 $A_i$ 服从均值为0，方差为 $\rho$ 的正态分布， $B_{ij}$ 服从均值为0，方差为 $1-\rho$ 的正态分布。参数 $\rho$ 表示不同类间的异质性， $1-\rho$ 则表示同一类内不同对象的异质性，其中 $\rho$ 取三种情况分别为0.25，0.5，0.75。该模拟重复进行500次。上述条件下的模拟结果如表1，表2，表3所示，其中EST，SE，ESE和CP分别代表参数估计的均值，样本标准差，标准差的渐近估计，以及正态近似条件下， ${\beta }_0$ 的95%置信区间下的覆盖率。从表1~3中的EST，SE，ESE和CP值都可以看出，当样本量变大时参数估计的均值越接近真值，随着样本量增加样本标准差和标准差的渐近估计越来越接近，CP也越来来越近似于95%，可以得到本文提出的估计方法模拟效果良好，在其他参数设置下，得到结果是差不多的。

Table 1. Estimation for β0 = (0.5, 0.5)

表1. β₀为(0.5, 0.5)的估计

Table 2. Estimation for β0 = (1, 0.5)

表2. β₀为(1, 0.5)的估计

Table 3. Estimation for β0 = (0.5, 1)

表3. β₀为(0.5, 1)的估计

4. 应用

在这部分我们采用提出的方法分析一个临床医学数据 [12] gamma干扰素治疗慢性肉芽肿性疾病的研究。数据共有128名慢性肉芽肿性疾病患者，被随机分为两个组，gamma干扰素组和安慰剂组，每个病例的数据给出了患者发生重复严重感染的时间，在进行中期分析时，65名安慰剂患者中的20名和63名gamma干扰素患者中的7名都至少经历过一次严重感染。在这里，我们把每一个个体视作一个簇，每个个体的各次复发的间隔时间视为簇中的成员。

假设数据可以由加性–乘积模型拟合，即 ${\lambda }_{ij}\left(t|Z_{ij},W_{ij}\right)={\lambda }_0\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\beta }+W_{ij}^{\text{T}}\gamma$，定义 $Z_{ij}$ 为治疗代码，如果病人接受gamma干扰素治疗则取1，如果病人在安慰剂组则取2， $W_{ij}$ 为规范化后的个体年龄。

通过本文的方法可以得到的 $\beta ,\gamma$ 的估计分别为： $\hat{\beta }=0.\text{7827}$， $\hat{\gamma }=-0.00\text{23}$，标准差分别是0.2242和0.0011，检验P值分别为2.3996 × 10⁻⁴和0.01689，根据 $\hat{\beta }$ 的值的大小，能够得出当 $Z_{ij}=1$ 时比 $Z_{ij}=2$ 基准风险率函数低，由此可见用gamma干扰素治疗的风险比安慰剂组的风险更低，而且P值小于0.05，说明gamma干扰素治疗能显著降低感染慢性肉芽肿病的风险率函数，根据 $\hat{\gamma }$ 的值的大小以及相应的P值，可以得出年龄越大感染慢性肉芽肿病的风险显著地越低。具体地，固定年龄时，干扰素治疗组的风险率在时刻t时比安慰剂组的风险率绝对数值降低 ${\hat{\lambda }}_0\left(t\right)\times 2.5972$，固定治疗组别时，年龄每增加10岁，风险率的绝对数值降低4.8 × 10⁻⁴。另外我们给出累积的基准风险率函数的估计 ${\displaystyle {\int }_0^t{\hat{\lambda }}_0\left(t\right)\text{d}t}$，由它可以得到 ${\hat{\lambda }}_0\left(t\right)$ 在每个时刻的近似估计，见图1 (横坐标为所有个体的复发事件的间隔时间t，单位为天)。

Figure 1. Estimation for ${\displaystyle {\int }_0^t{\hat{\lambda }}_0\left(t\right)\text{d}t}$

图1. ${\displaystyle {\int }_0^t{\hat{\lambda }}_0\left(t\right)\text{d}t}$ 对时间的函数图像

为了对模型的拟合优度进行检验，我们对残差进行分析：我们来绘制残差 ${\hat{r}}_{ij}$ 关于个体复发 $i=1,2,\mathrm{...},128,j=1,2,\mathrm{...},n_i$ 的散点图，见图2 (横坐标为所有个体的复发的标识，128个个体共有203个复发)，其中

${\hat{r}}_{ij}={\displaystyle {\int }_0^{\tau }\text{d}{N}_{ij}\left(t\right)}-Y_{ij}\left(t\right)\left[{\hat{\lambda }}_0\left(t\right){\text{e}}^{Z_{ij}^{\text{T}}\hat{\beta }}+W_{ij}^{\text{T}}\hat{\gamma }\right]\text{d}t$

残差图可看出，残差随机分布在[−2, 2]中，因此不拒绝给出的模型。

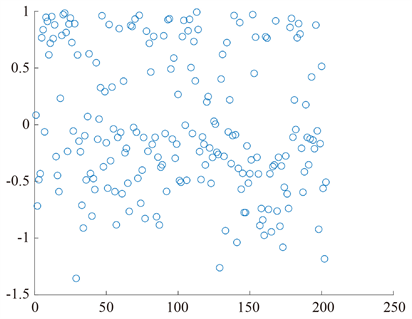
Figure 2. Scatter of residual vs. individual

图2. 残差对个体的散点图

5. 总结

在这篇论文中，我们对聚类失效时间建立了边际加性乘积风险率函数模型，应用估计方程的思想进行统计推断，在计算中，我们使用了牛顿迭代法，得到参数的估计，应用大数定律证明估计量的相合性，应用中心极限定理证明估计量的渐近正态分布，并给出估计量的渐近方差，然后进行数值模拟验证提出的方法，模拟结果表现较好，最后将提出的模型和方法应用于实际数据，找到gamma干扰素治疗和年龄对慢性肉芽肿病的影响方式。未来我们将考虑在模型中加入随机效应项表示同一类之间的相关性，利用的数据信息更充分，相应的估计方法也更具有挑战性。