射流冲击不同形状凸起热源的数值模拟研究

Numerical Simulation of Jet Impact on the Protruded Heat Sources with Different Shape

摘要: 冲击射流是一种换热性能突出的散热方式，被广泛应用于电子信息、航空航天、军工国防等领域。该研究以水为工质，数值模拟研究了二维层流射流冲击矩形、三角形及圆弧形凸起热源的流动与换热特性，对比研究了冲击距离(h/W)在1~10范围内，雷诺数在50~250范围内的换热规律。研究表明：体积夹带量随着雷诺数与冲击距离的增加而增加，且几乎不受凸起热源形状变化的影响。在滞止点附近，三角形凸起热源的局部换热效率极高，在冲击距离h/W = 1、Re = 50时，其最大换热系数是矩形的1.84倍，圆弧形的1.77倍。从热阻与泵功角度分析，冲击距离h/W = 1的矩形凸起热源有着最优的换热性能。该研究丰富了冲击射流强化换热理论，为解决高热流密度冷却技术提供了理论依据。

Abstract: Impinging jet cooling is an outstanding heat dissipation method, which has been widely applied in the areas of electronics, aerospace, military and defense, automobile and medical industries. Using water as the working fluid, the flow and heat transfer performance of two-dimensional laminar jet impinging on rectangular, triangular and circular convex heat sources are numerically studied, and systematically evaluated with the impact distance (h/W) in the range of 1~10 and Reynolds number in the range of 50~250. The results show that the volume entrainment increases with the increase of Reynolds number and impact distance, without much affected by the convex shape. Near the stagnation point, the local heat exchange efficiency of triangular heat source is the best one. When the h/W = 1 and Re = 50, its maximum heat exchange coefficient is 1.84 times that of rectangle and 1.77 times that of circular arc, respectively. From the thermal resistance and pump power perspec-tives, the rectangular heat source with h/W = 1 shows the best performance. This study enriches the heat transfer theory of jet cooling, providing design guidelines for the cooling technology towards high heat flux.

1. 引言

相比传统对流换热，冲击射流因其速度场与热流场的协同性好，在滞止点附近可以形成非常薄的边界层，而有着显著的换热优势 [1] [2]。目前，冲击射流冷却已成为传热领域学者的研究热点，被广泛应用于航空发动机涡轮叶片冷却、食品干燥、金属热处理、电子器件冷却等领域。

影响冲击射流换热的因素有很多，如喷嘴数量、喷嘴形状、冲击高度、被冲击面的粗糙度以及边界条件等 [3] - [14]。Lin [15] 等研究了狭缝射流中的不同雷诺数和冲击高度对加热靶面换热特性的影响，得出靶面的换热效率随着雷诺数的增加而增加，但是受冲击高度的影响并不明显。在二维层流壁面射流的条件下，Kanna [16] 等数值求解了后阶梯流动受阶梯不同几何形状和不同雷诺数的影响规律，发现射流的卷吸作用随雷诺数的升高而增强。Ekiciler [17] 等对比分析了空气射流冲击平面、三角形及正弦形三种靶面对传热特性的影响。Chan [18] 等采用瞬态加热液晶技术研究了湍流射流冲击半圆形凸表面的换热特性，得出半圆形凸表面的平均Nu数随着Re数的增加而增加，随着冲击高度的增加而减少。对卷吸作用研究上，Sriegl [19] 等建立了单股射流的热夹带关联式，并分析了夹带流体温度对湍流射流局部换热的影响。Ganguly [20] 等对层流射流冲击矩形凸起热源进行了模拟研究，并在开放边界下，详细分析了射流卷吸作用及靶面的换热特性受不同雷诺数和冲击高度的变化关系。

综上可见，目前对射流冲击凸起热源的研究很少，但在实际工业应用中，被冲击的表面却不总是平直的，可能会有各种形状的凸起，因此对不同形状的凸起热源进行研究十分必要且很有意义。本文基于有限单元法，对二维层流射流冲击矩形、三角形、圆弧形三种凸起热源进行了数值模拟，并在开放边界下，分析了不同雷诺数、不同冲击高度(h/W)及三种形状的凸起热源对卷吸作用和被冲击表面的换热规律，以及从热阻与泵功的角度综合比较了各凸起热源的特性。

2. 物理模型与数值方法

2.1. 物理模型

射流冲击凸起热源的物理模型如图1所示，水从直径为W = 1 mm的喷嘴中流出，对高度D为2 mm、半长l为6 mm的凸起热源进行冲击冷却，凸起热源有三种不同的形状，分别为矩形、三角形及圆弧形，如图1(a)~(c)所示，其中圆弧形的圆弧半径为10 mm，圆心在对称轴的延长线上。模型在宽度方向上具有对称性，在此选用一半进行计算分析，其中高度H为15 mm，宽度L为20 mm，喷嘴壁厚w = 0.25 mm，冲击高度h/W在1~10之间。入口温度为291.15 K，从自由边界进入的水的温度与入口温度相同，入口雷诺数在50~250之间。

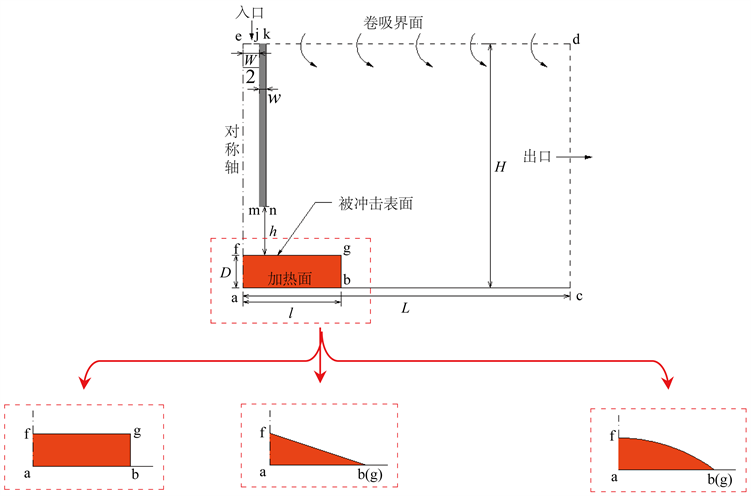(a) 矩形凸起热源 (b) 三角形凸起热源 (c) 圆形凸起热源

Figure 1. The model of protruded heat sources with different shape

图1. 不同形状凸起热源的冲击模型

2.2. 控制方程和边界条件

假设二维层流冲击射流为不可压缩的定常流动，质量、动量、能量守恒方程如下所述：

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$ (1)

$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial x}+v\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)$ (2)

$u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial y}+v\left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}\right)$ (3)

$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \left(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}\right)$ (4)

其中，u、v分别为x、y方向上的速度分量，ρ为流体的密度，ν为运动粘度，α为热扩散率。

喷嘴入口区域ej：u = 0，v = v_i，T = 291.15 K；自由边界kd选择压力入口：p = p_g = 0；对称边界ae：u = 0，¶v/¶x = 0，¶T/¶y = 0；出口边界cd：¶u/¶x = 0，¶v/¶x = 0，¶T/¶x = 0，p = p_g = 0；壁面fg(gb)采用无滑移热耦合边界：u = v = 0；壁面ab为恒定热流：q = 25 W/cm²；壁面bc及jmnk采用无滑移绝热边界条件：u = v = 0。

2.3. 计算方法、网格无关性验证及计算结果验证

本数值研究采用有限体积法对控制方程组进行离散，并运用SIMPLEC耦合式解法求解动量方程。用瞬态方法进行计算，且时间步长设置为0.1 s。当所有参数的残差值小于10⁻⁶时，判定解收敛。以Re = 50、冲击高度h/W = 1的矩形凸起热源为例，来验证网格的独立性。本研究绘制了四种类型网格，其中结构性网格m1数为38251，非结构性网格m2数为35422、m3为69022个、m4为121909个，对此计算出fg面Nu数分别为4.08、3.98、4.11、3.97，相差误差极小且不大于3.5%，因三角形与圆弧形凸起热源无法绘制结构性网格，因此本研究统一选用m3非结构网格进行计算。

为了验证模拟结果的准确性，本文以水为工质，并取h/W = 1、Re = 50时，对Ganguly [20] 中的模型进行了模拟，将模拟的Nu与Ganguly [20] 中的结果进行对比，两者仅相差2.01%。

3. 结果与讨论

3.1. 卷吸分析

当流体以一定速度从喷嘴流出时，流动的流体会与周围的静止流体间形成一定的速度差，进而形成速度不连续的间断面，而速度间断面的状态不稳定就会产生波动，并发展成漩涡，将周围的流体不断的卷吸进来，此间也会有区域外的流体通过自由边界被夹带进来。随着周围流体与射流流体不断的掺混，这对射流主流流体形成了一定的阻力，使射流流体的速度降低，减小了对靶面的冲击速度 [21]，进而影响换热。

不可压缩流体平面运动的流函数：dψ = −vdx + udy，其物理意义是：1) 在流函数云图中，等流函数线就是流线。2) 流函数云图中任意两条流线的流函数之差等于通过其间单位深度的流量。如图2，观察图中流线可以发现，确有流体从区域外通过自由边界被卷吸进入区域内部，在Re为50、冲击距离h/W为1时，三种不同形状凸起热源的流线分布近乎相同，被夹带进来的流体量相差不大。

Figure 2. Flow function contours of the protruded heat sources with Re = 50 and impact distance h/W = 1

图2. Re = 50、冲击距离h/W = 1的不同形状凸起热源的流函数云图

在冲击距离h/W = 1、10，凸起热源形状分别为矩形、三角形及圆弧形时，通过自由边界被夹带到区域内的单位深度流体的质量流量随Re数变化的曲线如图3(a)所示，其中d代表模型的深度。从中可以发现，随着雷诺数的增加，被夹带进来的流体的质量流量也随之增加。并且在雷诺数较小(50~150)时，夹带进来的流体的质量流量对Re数依赖性很高，在冲击距离h/W = 10时，通过开放边界的流体质量流量变化程度明显大于冲击距离h/W = 1时的。

图3(b)反映了在Re = 50、250时，被夹带到区域内的流体的质量流量随冲击距离h/W的变化曲线。从中可以看出，随着冲击距离h/W的增加，被卷吸进来的流体质量流量也随之增加。观察图2、图3可以发现，被夹带进来的流体的质量流量几乎不受凸起热源的形状变化所影响。

(a) 夹带的质量流量随Re数的变化规律 (b) 夹带的质量流量随h/W的变化规律

Figure 3. Variation law of entrainment mass flow rate

图3. 夹带质量流量的变化规律

3.2. 冲击表面的换热特性分析

3.2.1. 边界层分析

对式(2)进行数量级分析，可得出层流边界层的动量方程如下式 [22]：

$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{\rho }\frac{\partial p}{\partial x}+v\frac{{\partial }^{2}u}{\partial y^2}$ (5)

从式(5)中可以看出，速度边界层内的流体流动主要受到三种力，惯性力、压强梯度力以及粘性力。其中惯性力可以驱使流体向前流动，粘性力则会阻碍流体的流动，而压强差在顺压梯度区会使流体加速，在逆压梯度区使流体减速 [22]，其中边界层脱离现象常常发生在逆压梯度区，而速度边界层的脱离会削弱传热过程。

冲击距离h/W = 1、Re = 50时的速度矢量云图如图4所示，从中发现，三种不同形状的凸起热源均在较早处出现了速度边界层脱离的现象，这是因为，当Re = 50时，流体的惯性力较小，不足以克服阻碍流体运动的粘性力和压强差，因此壁面附近的流体出现了静止甚至向上游运动的情况，以至于发生了速度边界层脱离的现象。

在Re = 50、冲击距离h/W = 1时，三种形状凸起热源的温度云图如图5所示，从中可以看出，在对凸起热源进行射流冲击时，滞止点附近的温度边界层极薄，随着远离滞止点，温度边界层渐渐变厚。并且还可以发现，接近末尾处，圆弧形凸起热源的温度边界层最厚，三角形次之，平面的则最薄，这直接导致了三种凸起热源换热效果有了明显差别，这一情况在图6中可以更清晰的看见，在沿程距离x = 4 mm左右时，三种形状凸起热源的换热系数开始发生了明显的分别。

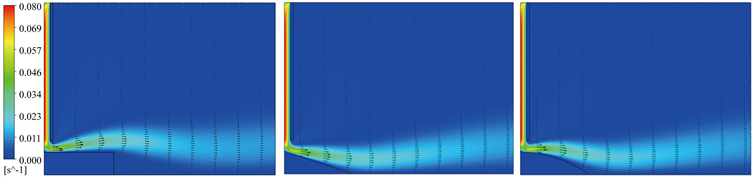
Figure 4. Velocity contours when Re = 50 with impact distance h/W = 1

图4. Re = 50、冲击距离h/W = 1时的速度矢量云图

Figure 5. Temperature contours when Re = 50 and impact distance h/W = 1

图5. Re = 50、冲击距离h/W = 1时的温度云图模型

Figure 6. Heat transfer coefficient along the impact surface with h/W = 1 and Re = 50

图6. h/W = 1、Re = 50时被冲击面的沿程换热系数

3.2.2. 被冲击靶面沿程换热系数与平均Nu的分析

在冲击距离h/W = 1及Re = 50时，被冲击面的沿程换热系数如图6所示。从图6中可以发现，在滞止点附近，三角形凸起热源的局部换热系数相较于矩形与圆弧形凸起热源有着明显的优势，在此工况下，三角形凸起热源换热系数的最大值分别是矩形与圆弧形凸起热源的1.84倍与1.77倍。并且在其他工况下，三角形凸起热源同样都着明显的局部换热优势。

图7(a)反映了在冲击距离h/W = 1时，三种不同形状凸起热源的靶面平均Nu随Re的变化规律。从中可以发现，随着雷诺数的升高，三种不同形状凸起热源的被冲击表面平均努塞尔数均随之增大，当Re升高时，流体的动能增大，射流冲击靶面时，可以减薄边界层，从而强化传热。

图7(b)反映了在Re = 50时，三种不同形状凸起热源被冲击表面的平均Nu随冲击距离h/W的变化规律。从中可以看出，在Re = 50时，随着冲击距离h/W的增加，三种不同形状凸起热源的被冲击表面平均努塞尔数均随之减小。从图7中还可以发现，矩形凸起热源的平均Nu最大，三角形凸起热源略次之，圆弧形凸起热源最小。

(a) 被冲击表面平均Nu随Re的变化规律 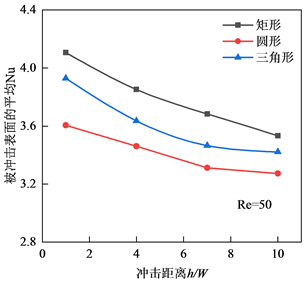(b) 被冲击面平均Nu随h/W的变化规律

Figure 7. Average Nu on the impact surface

图7. 被冲击表面平均Nu的变化规律

3.2.3. 泵功分析

为了权衡的考虑射流冲击凸起热源的传热与功耗的性能，在此研究了不同冲击距离h/W下，三种不同形状凸起热源的热阻与泵功的函数关系，如图8，其中d代表模型的深度。当通过提高流体的流速来增加射流冲击的传热性能时，泵的功耗也将随之增加，因此对各个模型同时进行热阻与泵功的分析十分有必要。为了得到性能最优的模型，热阻与泵功都应尽可能的小，观察图8发现，在单位深度时，模型的泵功都比热阻小一个数量级，所以从热阻与泵功的角度分析，冲击距离h/W=1的矩形凸起热源的性能最优。

Figure 8. Relationship between thermal resistance of convex heat source and pump work function

图8. 凸起热源的热阻与泵功函数关系

4. 结论

本文运用数值模拟方法研究了射流冲击凸起热源换热特性，在不同的冲击距离h/W及不同的Re下，对比分析了三种不同形状凸起热源的流动和换热特性，得出以下结论：

1) 通过自由边界被夹带进来的流体质量流量，随雷诺数和冲击距离的增加而增加，并且不受凸起热源形状变化的影响。

2) 在滞止点附近，相较于矩形及圆弧形凸起热源，三角形凸起热源的局部换热系数有着明显优势，在冲击距离h/W = 1、Re = 50时，其最大值是矩形凸起热源的1.84倍，是圆弧形凸起热源的1.77倍。

3) 三种热源冲击表面的平均Nu随着Re的升高而增大。在Re = 50时，被冲击靶面的平均Nu数随着冲击距离h/W的增加而增大。且在冲击距离h/W = 1、Re = 50时，矩形凸起热源的被冲击靶面的平均Nu数最大、三角形略次之，圆弧形凸起热源最小。

4) 从热阻与泵功角度分析，冲击距离h/W为1的矩形凸起热源的性能最优。