1. 引言
弹性杆在机械载荷作用下的过屈曲和变形问题在工程实践中具有极广泛的应用。例如作为钻杆、电子信号发射连接件、机器人臂、跳高撑杆等,近30年,在生命科学领域之中将弹性大变形杆作为生物大分子链(DNA等)的力学模型 [1] [2]。
1744年Euler等 [3] 研究了弹性细杆的平衡和稳定性问题。1927年Love等 [4] 进一步研究了细长杆的弹性曲线问题,细长弹性杆的几何非线性问题作为结构大变形的问题之一始终受到广泛重视。Kicrhhoff理论(即弹性杆静力学非线性理论)建立于1859年。Kicrhhoff理论其实质为利用欧拉-泊松(Euler-Poison)方程以及弹性杆平衡微分方程两者在数学形式中的相似性,将拉格朗日情形刚体定点转动的解析积分进行移植,以用来解决弹性杆的平衡问题 [5]。Pflǜger [6] 是第一位研究压杆在轴向压缩变形下对屈曲变形影响的人。Antanackvic [7] 等采用了分析方法研究在端部压力作用下可伸长简支梁过屈曲的分叉解,并得出了和细长比相关的临界载荷解析式。Gummadi和Palazotto [8] 对梁、拱中的大变形问题进行了研究,对现代大变形力学问题的研究产生了极大的影响。基于连续介质一般理论,Filipich和Rosales [9] [10] 系统推导出弹性细杆在轴向压力作用下的几何精确非线性控制方程,推导出了弹性压杆在9种本构关系下的过屈曲模型以及数值解,并研究在轴向载荷作用下弹性杆本构关系不同时对过屈曲行为的影响。Plaut等 [11] 基于弹性杆的轴线不可伸长几何非线性理论,采用打靶法对问题数值求解,分析了在外载荷作用下预弯曲杆在与刚性平面发生接触后的屈曲和变形问题。
薛纭等 [12] 和刘延柱等 [13] 基于弹性杆的几何非线性模型,同时考虑了横向剪切变形和杆的轴线伸长,得出了较为精确的Cosserat弹性杆模型。李世荣 [14] [15] [16] 等基于轴线可伸长杆的基本模型,采用了打靶法进行数值求解,对弹性压杆在几种不同边界条件下的过屈曲问题进行分析。郭锐 [17] 等研究了在中点附近点约束下的弹性细杆两端受压时的过屈曲变形,并给出了与轴向载荷和约束力相关的弹性杆的平衡构形以及平衡路径。李银山 [18] 等在研究弹性压杆的大变形问题时,采用了曲线积分的方法,得到了压杆过屈曲大变形的理论结果。薛纭等 [19] 于2019年基于弹性细长杆Kirchhoff动力学的比拟方法,从Kirchhoff弹性杆以及Cosserat弹性杆的拉格朗日方程出发,研究出了在弯扭度以及形心应变矢发生突变时的拉格朗日方程,并分析了弯扭度与形心应变矢突变对弹性杆挠曲线的影响。为弹性细长杆弯扭度发生突变提供了力学方法。刘荣刚等 [20] 采用能量法和挠曲线近似微分方程方法得出了临界力极限表达式,解决了细长弹性压杆临界力作用下的挠度不确定问题。
本文拟采用可伸长杆的基本理论,在精确的几何模型下推导线弹性变形杆的几何方程和平衡方程,并用打靶法数值求得压弯变形的数值解。
2. 控制方程
考虑一长为
的矩形截面
压杆,一端固定一端自由,在自由端作用集中力
和弯矩
(见图1)。
2.1. 几何方程
将杆的轴线置于直角坐标系
,记变形前杆内任意一点为
,轴线上的点
,
,杆发生弯曲变形后,轴线上点的坐标变为
,其中
和
分别为
方向的位移,假设变形服从Kirchhoff直线法假设,由轴线可伸长梁的大变形理论,可得如下几何关系:
(1)
(2)
(3)
(4)
其中:
为横截面转过的角度,梁的轴线在变形后为平面曲线,
为变形后的弧长,
为轴线弯曲后的曲率,
为轴线的伸长比。
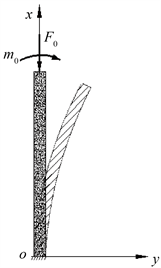
Figure 1. Mechanical model of structure
图1. 结构的力学模型
轴线应变
为
横截面内任意一点的应变为
2.2. 物理方程
考虑应力—应变的线弹性关系,横截面上的正应力为
横截面上的轴力
和弯矩
为
其中:
为杆的横截面面积,
为横截面的抗弯刚度。
2.3. 平衡方程
在精确几何模型下研究变形后微段
上的受力平衡。用
表示横截面上的内力,则
,轴力和剪力分别为
利用平衡条件可得以下平衡方程
将物理方程带入以上平衡方程中得
(5)
(6)
式(1)~(6)构成了弹性杆在精确几何模型下非线性大变形问题下的基本方程。考虑具体边界条件,就构成杆件压弯大变形的边值问题,对于一端固定另一端自由的弹性杆,相应的边界条件为
(7)
(8)
文献 [9] [10] 研究了弹性杆在端部压力和剪力作用下的过屈曲问题。基于Kirchhoff假设推导出的非线性基本方程不适用于弯曲变形过大的情况。
3. 对控制方程无量纲化
引入下列无量纲量
其中:
为杆的细长比。将无量纲量代入物理方程可得无量纲轴力和弯矩的表达式
(9)
将无量纲量代入式(1)~(8),可得以下无量纲基本方程
(10)
(11)
(12)
(13)
(14)
(15)
无量纲边界条件为
(16)
(17)
4. 弯曲问题的数值分析
由于微分方程的强非线性以及多未知量间的耦合效应,难以获得问题的解析解,因而采用打靶法对此边值问题进行数值求解。取
,研究自由端的位移随端部无量纲载荷的变化规律。
采用打靶法求解,令:
(18)
问题的控制方程可写为一阶常微分方程组:
(19)
(20)
(21)
边界条件为:
(22)
(23)
当端部载荷增加时,可以求解出弯曲程度较大的情形,说明方程(1)~(6)采用了精确的几何模型,对问题的求解适应大变形的弹性变形问题。文献 [18] 采用了微分求积法,建立大变形时弹性压杆的数学模型,并采用Maple编程对此模型进行了求解,得到自由端压力,转角,挠度和轴向位移的对应数值关系,其数值结果与本文结果基本一致。
图2为端部弯矩
为0.1时,不同轴向压力
的平衡构形。随着杆端轴向压力
增加,弹性杆弯曲程度逐渐增大,并发生回弯(横向位移减小)。杆件的变形过程与文献 [18] 的结果是一致的。
图3给出了不同
时,轴向位移
随
的变化规律。图中可以看出,随着
的增加,轴向位移不断(负向)增加,在
较大时,不同
的变化规律是类似的,而在
较小时,差异较大。
三条曲线,轴向位移
几乎从0开始,当
时,
变为从-0.36开始。压杆稳定的无量纲临界载荷的Euler公式为
在
时,
达到临界载荷前,压杆的轴向位移几乎为0,而达到临界载荷后,轴向位移明显增加,变形从轴向压缩变形过渡到过屈曲变形。
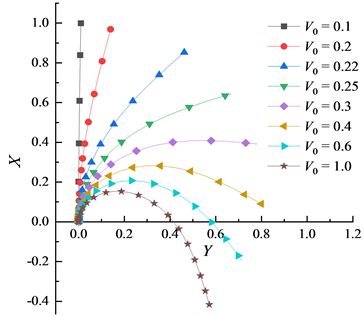
Figure 2. Equilibrium configurations at
图2.
的平衡构形

Figure 3. Variation curves of
with
图3.
随
的变化曲线
图4给出了不同
时,横向位移
随
的变化规律,当
小于临界载荷时,曲线从0附近开始增加,当
大于临界载荷时处于过屈曲平衡,此时
时已经出现了横向位移。
较小时,曲线在
附近出现变化,此时变形开始回弯(见图2)。当
较大时,过屈曲变形较大,挠度随
增加而减小,回弯现象更为明显。
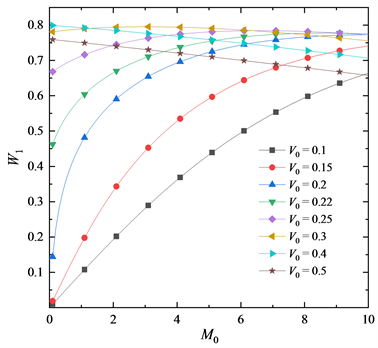
Figure 4. Variation curves of
with
图4.
随
的变化曲线
图5给出了不同
时,轴线长度随
的变化规律。图中可以看出,在轴向压力作用下,随着
的增加,轴线的长度是增加的,图像说明随着弯曲变形的增加,
引起轴线变形量下降。
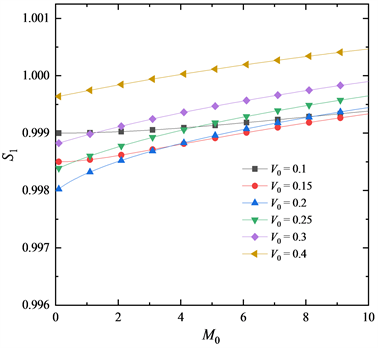
Figure 5. Variation curves of
with
图5.
随
的变化曲线
图3~5反映出:
较小时对杆变形影响在前屈曲阶段
和过屈曲阶段
是不同的,此时
对变形过程影响明显。而当
较大时,前屈曲阶段和过屈曲阶段的变形规律基本一致,
对变形过程的影响减弱。

Figure 6. Variation curves of
with
图6.
随
的变化曲线
图6给出不同端部外力偶
作用时,轴向位移随
的变化曲线,图中可以看出,随着
的增加,端部轴向位移是(负向)增加的。在
较小时,不同的
对应的变化曲线差异较大,
时,能明显的看出由弯曲变形到过屈曲阶段的过程,临界载荷在
附近;而
时,
引起的变形较大,前屈曲到过屈曲的变化并不明显。当端部压力
时,不同
引起的轴向位移差异变得很小。
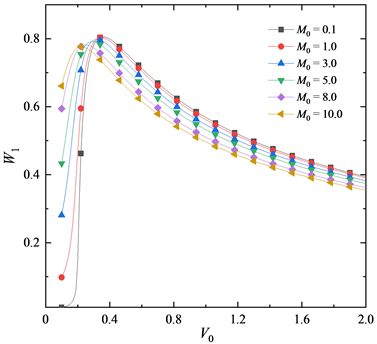
Figure 7. Variation curves of
with
图7.
随
的变化曲线
图7给出了不同
时,横向位移
随
的变化规律,图中可以看出,随
的增大,横向位移先增后减,
存在最大值。随
增大最大挠度点横向偏移,对应的
在数值上减小。当
时,能明显看出随
的增加,变形由前屈曲到过屈曲阶段的变化过程,当
较大时,此过程不明显。
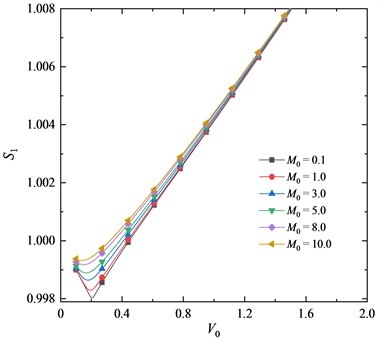
Figure 8. Variation curves of
with
图8.
随
的变化曲线
图8给出了不同
时,轴线长度
随
的变化规律。图中可以看出,随着
增大,
呈现先减后增的趋势。
较小时,
减小到增大的转折点较明显(临界载荷附近),当
较大时,
从减到增,变化比较平缓。
图6~8反映出:当
较大时,不同
时的变形规律基本相同,当
较小时,尤其是在临界载荷附近,不同
时的变形过程差别较大。
5. 结论
本文导出了一端固定一端自由约束的弹性杆在外荷载下压弯变形问题的精确几何模型的基本方程,根据求得的数值解,绘出了弹性杆在端部外荷载作用下的压弯构形和非线性平衡路径,并精确分析了外载荷对弹性杆变形的影响。得出了以下结论:
1) 本文基本方程采用了大变形下精确的几何模型,既可求解压杆的过屈曲问题,也可精确求解杆件的大变形弯曲问题。
2) 由精确几何模型下的基本方程求得的小变形时的数值结果与参考文献中的结果基本一致,而本文的基本方程更为精确。
3) 弹性杆压弯变形时,杆件变形随
的变化规律受到
的影响,在
较小时,
的影响比较明显。同时杆件变形随
的变化规律也受到
的影响,当在
临界载荷附近以及小于临界载荷时,
对变形的影响较为明显;随
的增大,
对变形的影响逐渐减弱。
基金项目
本文得到国家自然科学基金11862012的资助。