1. 引言
悬臂梁是较为常见的一类受力构件,工程中的悬臂梁变形主要表现为弯曲变形,因此,研究悬臂梁的弯曲变形问题具有重要的实际意义。悬臂梁的弯曲变形问题可以划分为小变形和大变形两类问题,其中关于悬臂梁在横向力作用下的小变形弯曲问题的分析和求解在各种版本的材料力学教科书(如 [1] [2] [3] [4] [5] )中都有过详细介绍,由于此类问题最终可以简化为线性常微分方程(挠曲线近似微分方程)的初值问题的解,因此,对于这类问题的分析和求解就显得相对容易和简单。相比之下,悬臂梁在横向力作用下的大变形弯曲问题的分析和求解就复杂了许多。在大变形弯曲下,由于梁变形的几何非线因素不可忽略,因此,在分析悬臂梁的大变形弯曲问题时,不仅需要考虑梁轴线上点的横向位移(挠度),而且还需要考虑梁轴线上点的轴向位移,由此所建立的描述悬臂梁大变形弯曲问题的数学模型通常是一组复杂的非线性微–积分方程组。这方面比较典型的具有代表性的工作是王逸维等 [6] 所建立的描述悬臂梁在横向力作用下的大变形弯曲问题的非线性微–积分方程组,他们通过MATLAB数值方法求对该方程组进行了求解,获得了悬臂梁在相应横向力作用下的大变形挠曲线。
本文研究等截面悬臂梁在轴向压力和横向力联合作用下的小变形和大变形弯曲问题,研究该问题的关键在于计入轴向压力在梁的弯曲变形中所产生的附加弯矩的贡献因素。本文在计入这一因素的基础上,导出了适合在小变形情形下确定等截面悬臂梁在轴向压力和横向力联合作用下的挠曲线解析函数;另外,还建立了适合在大变形情形下描述等截面悬臂梁在轴向压力和横向力联合作用下的挠曲线数学模型及其计算这种大变形挠曲线的方法。
2. 悬臂梁在轴向压力和横向力联合作用下的小变形弯曲
如图1所示,一根等截面悬臂梁的自由端承受轴向压力
和横向力
的作用,下面研究该梁的小变形弯曲问题。
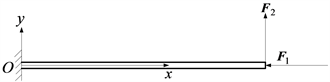
Figure 1. A cantilever beam subjected to axial pressure and transverse force
图1. 承受轴向压力和横向力联合作用的悬臂梁
应用截面法,取横坐标为x的横截面到自由端的这段梁为研究对象,画出该段梁在弯曲变形位置时的受力图(图2),图中的
、
和M分别表示横坐标为x处的横截面上的轴力、剪力和弯矩(图中的轴力、剪力和弯矩都按正方向画),
表示此截面形心的挠度。由该段梁的力矩平衡方程,可以推得弯矩M的表达式为
(1)
式中,l为梁的全长,该式中的画线项是轴向压力
在梁的弯曲变形中所产生的附加弯矩,显然这种附加弯矩只有把梁段的变形位置(图2)作为静平衡位置进行分析,才能计入它对总弯矩的贡献。
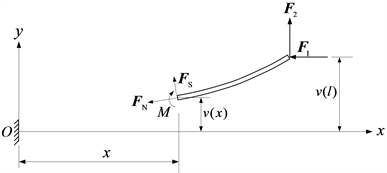
Figure 2. Free-body diagram of the beam from the cross section of abscissa x to the free end in the bending deformation position
图2. 横坐标为x的横截面到自由端的这段梁在弯曲变形位置时的受力图
将式(1)代入到梁的挠曲线近似微分方程
(该方程仅适用于梁的小变形情形 [4] )后,得到
(2)
上式中的画线项代表了轴向压力对于梁的弯曲变形所产生的影响。
悬臂梁的边界条件为
,
(3)
可以求得方程(2)且满足边界条件(3)的解为
(4)
这就是等截面悬臂梁在其自由端承受轴向压力和横向力联合作用时的挠曲线解析函数,需要说明的是该函数仅适用于梁的小变形弯曲情形。
3. 悬臂梁在轴向压力和横向力联合作用下的大变形弯曲
下面研究如图1的等截面悬臂梁在轴向压力和横向力联合作用下的大变形弯曲问题。为此,从梁的根部开始,沿着梁的轴线取弧坐标为s的横截面到自由端的这段梁为研究对象,画出该段梁在弯曲变形位置时的受力图(图3),图中的
、
和M分别表示弧坐标为s处的横截面上的轴力、剪力和弯矩(这里
、
和M的方向都按正方向画出),由该段梁的静力学平衡方程,可以推得剪力
的表达式为
(5)
式中,
为弧坐标为s处的横截面的转角(也就是梁的轴线在弧坐标为s处的切线相对于x轴的倾角,见图3)。
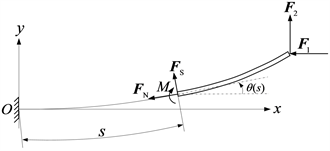
Figure 3. Free-body diagram of the beam from the cross section of arc coordinate s to the free end in the bending deformation position
图3. 弧坐标为s的横截面到自由端的这段梁在弯曲变形位置时的受力图
剪力
和弯矩M之间的关系又可表达为
(6)
考虑到弯矩M与曲率
之间满足关系 [7]
(7)
这里需要指出:只要在梁的材料的线弹性范围内,式(7)对于梁的小变形弯曲和大变形弯曲都是适用的。
将式(5)和式(7)代入式(6)后,得到
(8)
其边界条件为
,
(9)
而挠曲线上任意一点的横坐标
和纵坐标
又可用
表达为
(10)
(11)
这样式(8)~式(11)共同构成了等截面悬臂梁在轴向压力和横向力联合作用下的挠曲线数学模型,需要指出:该模型即适用于梁的大变形弯曲情形又适合于梁的小变形弯曲情形。由于此模型为非线性模型,所以一般很难求得其精确的解析解。可以采用如下的方法求其近似的数值解:首先应用Matlab bvp4c [8] (Matlab中求解非线性常微分方程两点边值问题的算法)求出方程(8)满足边界条件(9)的数值解,在此基础上,再应用式(10)和式(11)通过数值积分的方法求出挠曲线上各点的横坐标和纵坐标,最后,根据所求得的挠曲线上各点的横坐标和纵坐标具体画出梁的挠曲线。这就是等截面悬臂梁在轴向压力和横向力联合作用下的挠曲线计算(确定)方法。需要指出的是该方法对于梁的小变形弯曲和大变形弯曲都是适用的(只要变形在材料的线弹性范围内即可),不过在梁的小变形弯曲下,上述方法远不如直接应用只适合于小变形弯曲的式(4)来确定梁的挠曲线更为方便。
4. 算例
算例1 (小变形算例):如图1所示,等截面悬臂梁的自由端同时承受轴向压力
和横向力
的作用,其中
,
。梁的长度
,截面惯性矩
,弹性模量
。试确定该梁的挠曲线。
采用两种方法确定梁的挠曲线。
方法1:应用只适合小变形弯曲的式(4)确定梁的挠曲线形状;
方法2:应用本文第3节所述的方法(该法即适用于梁的小变形弯曲又适用于梁的大变形弯曲)确定梁的挠曲线形状。
图4中的实线和虚线分别是应用方法1和方法2所得到的梁的挠曲线。
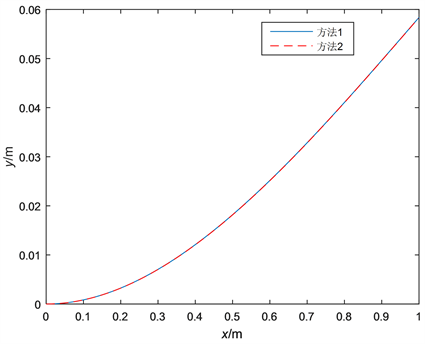
Figure 4. Small deflection curve of the beam
图4. 梁的小变形挠曲线
将图4中的实线和虚线相比较,可以看出:在梁的小变形情形下,应用上述两种方法所得到的挠曲线几乎重合。其中由方法1所求得的梁的自由端的挠度是0.0584 m,由方法2所求得的梁的自由端的挠度是0.0582 m,前者相对于后者的误差(相对误差)仅为0.3436%。这说明:在梁的小变形情形下,可以直接应用方法1(即直接应用式(4))更为方便地确定梁的挠曲线。
算例2 (大变形算例):如图1所示,等截面悬臂梁的自由端同时承受轴向压力
和横向力
的作用,其中
,
。梁的长度
,截面惯性矩
,弹性模量
。试确定该梁的挠曲线。
对于该算例仍然应用上述两种方法确定梁的挠曲线,并将两种方法得到的结果进行比较,并以此这说明:在梁的大变形情形下,方法1不再适用。
图5中的实线和虚线分别是应用方法1和方法2所得到的该梁的挠曲线。
将图5中的实线和虚线相比较,可以看出:在梁的大变形情形下,应用上述两种方法所得到的挠曲线有明显的差异。其中由方法1所求得的梁的自由端的横向位移(挠度)是0.6860 m (注意方法1即式(4)中未计入梁轴线上的点所发生的轴向位移),由方法2所求得的梁的自由端的横向位移(挠度)和轴向位移分别是0.4875 m和−0.1583 m,由此可知,在计算梁的自由端的挠度上,方法1相对于方法2的结果误差(相对误差)高达40.72%。这说明:在梁的大变形情形下,不能直接应用方法1确定梁的挠度,而应该采用方法2确定梁的挠度,否则会得到错误的结果。
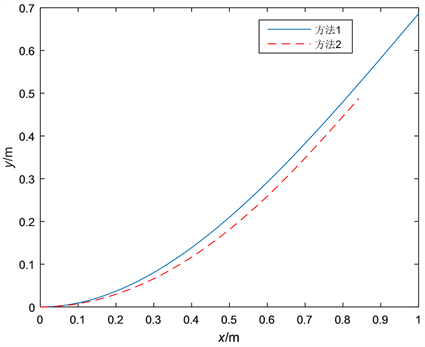
Figure 5. Large deflection curve of the beam
图5. 梁的大变形挠曲线
5. 结束语
针对等截面悬臂梁在轴向压力和横向力联合作用下的小变形和大变形弯曲问题的研究,本文分别取得了以下两项成果:1) 给出了适合在小变形情形下确定等截面悬臂梁在轴向压力和横向力联合作用下的挠曲线解析函数;2) 建立了大变形情形下的等截面悬臂梁在轴向压力和横向力联合作用下的挠曲线数学模型及其计算这种挠曲线的方法。